归纳三角函数、平面向量、数列、不等式中创新题的解法

■山东省肥城市泰西中学 梁乾旭

编者的话:“创新题追根溯源”栏目里的例、习题都非常新颖,有的是原创题,有的是改编题,每一道题都非常注重多解多变。当然,在注重数学阅读的高考大背景下,同学们还要把握核心考点,扩大知识视野,用扎实的基本功应对数学试题的万千变化。

数学中的创新题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求同学们在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的。

一个函数f(x),如果对任意一个三角形,只要它的三边长a、b、c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给出下列函数:①f(x)=x;②f(x)=x2;③f(x)=2x;④f(x)=lgx。其中是“三角保型函数”的是( )。

A.①② B.①③

C.②③④ D.③④

解析:任给三角形,设它的三边长分别为a、b、c,则a+b＞c,不妨假设a≤c,b≤c,对于①,f(x)=x,由于 a+b＞ a+b＞c＞0,因此函数f(x)=x是“三角保型函数”。

对于②,f(x)=x2,3,3,5可以作为一个三角形的三边长,但32+32＜52,不存在三角形以32,32,52为三边长,故f(x)=x2不是“三角保型函数”。

对于③,f(x)=2x,由于f(a)+f(b)=2(a+b)＞2c=f(c),所以f(x)=2x是“三角保型函数”。

对于④,f(x)=lgx,1,2,2可以作为一个三角形的三边长,但lg1=0不能作为三角形的边长,故f(x)=lgx不是“三角保型函数”。故选B。

点评:本题以“三角保型函数”为背景考查幂函数、一次函数、对数函数的性质。可通过新定义,把问题转化为已学过的知识求解。

设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若(λ∈R)(μ∈R),且2,则称A3,A4调和分割A1,A2。已知点C(c,0),D(d,0)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )。

A.C可能是线段AB的中点

B.D可能是线段AB的中点

C.C,D可能同时在线段AB上

D.C,D不可能同时在线段AB的延长线上

解析:根据已知得(c,0)-(0,0)=λ[(1,0)-(0,0)],即(c,0)=λ(1,0),解得c=λ。

由(d,0)-(0,0)=μ[(1,0)-(0,0)],解得(d,0)=μ(1,0),解得d=μ。

点评:本题通过新定义的“调和分割”考查共线向量、平面向量的坐标运算、不等式的性质,考查分类讨论思想。

(1)若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;

(2)判断(1)中的数列{Sn}是否为“特界”数列,并说明理由。

解析:(1)设等差数列{an}的公差为d,则a1+2d=4,S3=a1+a2+a3=3a1+3d=18,解得a1=8,d=-2,所以Sn=na1+

(2){Sn}是“特界”数列,理由如下:

综上,数列{Sn}是“特界”数列。

点评:本题以“特界”数列为背景考查等差数列的性质、求和公式、二次函数的性质。求Sn的最值时应注意n∈N*。

(2017年福建省福州文博中学模拟)《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺。大鼠日自倍,小鼠日自半。问:何日相逢,各穿几何?”题意是:有两只老鼠从墙的两边打洞穿墙。大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半。如果墙足够厚,Sn为前n天两只老鼠打洞长度之和,则S5=( )。

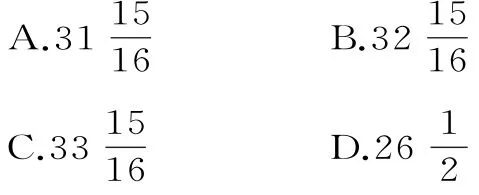
点评:本题以《九章算术》中的“两鼠穿墙题”为背景考查等比数列的性质、求和公式。考查了数学文化。