数列与不等式核心考点B卷答案
2017-12-04王伟
一、选择题
1.B 2.B 3.A 4.C 5.A 6.D 7.C 8.B 9.B 10.B 11.A 12.A 13.D 14.A 15.A 16.D 17.B 18.D 19.A 20.B 21.D 22.B 23.A 24.D 25.A 26.D 27.D 28.D 29.D 30.C
二、填空题

三、解答题
46.(1)设等差数列{an}的公差是d。因为a2+a7=-32,a3+a8=-40,相减可得(a3+a8)-(a2+a7)=2d=-8,所以d=-4。所以a2+a7=2a1+7d=-32,得a1=-2。所以an=a1+(n-1)d=-4n+2。
(2)由数列{an+bn}是首项为1,公比为2的等比数列,所以an+bn=2n-1,所以bn=2n-1-an=4n-2+2n-1。所以前n项和Sn=[2+6+10+…+(4n-2)]+(1+2+4+…+
47.(1)函数y=ax(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,而函数y=ax(a>0且a≠1)在[1,2]上单调递增或单调递减,所以a+a2=20,得a=4,或a=-5(舍去),所以a=4。




由数列{bn}的前n项和满足Sn-Sn-1=
Sn+Sn-1(n≥2),则(Sn-Sn-1)·(Sn+Sn-1)=Sn+Sn-1(n≥2)。又bn>0,Sn>0,所以 Sn-Sn-1=1。所以数列{Sn}构成一个首项为1,公差为1的等差数列,则 Sn=1+(n-1)×1=n,所以Sn=n2。当n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1,满足b1=c=1。


所以bn=2n-1(n∈N*)。x2>4/由x2>4,解得x<-2或x>2。而x2<-2的解集为∅,所以x的取值范围为{x|x<-2,或x>2}。
(2)对任意两个不相等的正数a、b,有a3+b3>2abab。
因为|a3+b3-2abab|-|a2b+ab2-2abab|=(a+b)(a-b)2>0,所以|a3+b3-2abab|>|a2b+ab2-2abab|,即a3+b3比a2b+ab2远离2abab。
53.(Ⅰ)不等式表示的平面区域如图1所示的阴影部分,当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,目标函数z=ax+by(a>0,b>0)取得最大值12,即4a+6b=12,即2a+3b=6,
(Ⅱ)若z的最大值不大于12,由(1)可的2a+3b≤6,a>0,b>0,画出平面区域,如图2所示。令Z=a2+b2+2(b-a),则可转化为(a-1)2+(b+1)2=Z+2=r2,圆心为(1,-1)。由图可知,当r=1时,最小,此时Z=-1;当圆过(0,2)时,半径最大,r=(1-0)2+(2+1)2=10,此时Z=8。因为a>0,所以Z>-1。因此Z=a2+b2+2(b-a)的取值范围(-1,8]。
54.(1)作GH⊥EF,垂足为H。
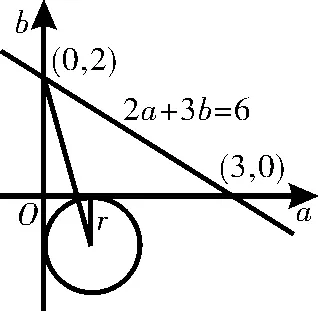
图2



图3

编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!

