定滑轮两侧绳内张力差及摩擦力分析
2017-12-02高彩云
高彩云
(山西大同大学物理与电子科学学院,山西大同037009)
定滑轮两侧绳内张力差及摩擦力分析
高彩云
(山西大同大学物理与电子科学学院,山西大同037009)
选择定滑轮和绳组成的质点系为研究对象,根据质点系角动量定理,计算了定滑轮两侧绳所受的张力差,并且分析了仅当定滑轮质量不能忽略时的情况。结果表明,滑轮两侧所受拉力与绳和滑轮的质量、轮的半径、轴摩擦力矩以及滑轮的角加速度有关,在极限情况下,滑轮两侧绳内张力趋于相等。定滑轮轮缘与绳子之间的静摩擦在促使滑轮加速转动。
张力;角动量;摩擦力;力矩;定滑轮
定滑轮实质是个等臂杠杆,根据杠杆平衡条件得出定滑轮可以改变力的方向,但不省力、不省距离的结论[1],定滑轮两侧绳内的张力是相等的,这是中学物理教材中对于定滑轮的界定。但是这个结论成立条件是滑轮是“理想”的,即滑轮质量、绳的质量轴承摩擦均不计,也就是常见的“轻绳”、“轻滑轮”、“滑轮光滑”等字眼,最典型的例子就是阿特伍德机。[2]事实上,绳的张力并没有直接作用在滑轮上,当滑轮转动时,绳的张力是通过转化为摩擦力矩或支承力矩间接起作用的。[3]并且,在滑轮运动的过程中,绳作用于滑轮的静摩擦力对滑轮做了功,但绳与滑轮之间的一对静摩擦力对系统做的总功为零,故系统的机械能守恒。[4]绳对轮缘的摩擦力矩的总和使轮子的角动量变化,而轮缘对绳元的摩擦力则与张力合力的切向分量平衡。[5]已有的文献侧重讨论的是滑轮中静摩擦力的问题,本文将重点分析定滑轮两侧绳内的张力的差与定滑轮的质量、绳的质量以及轴承的摩擦的具体定量关系。
1 质点系的总角动量
定滑轮系统如图1所示,将定滑轮视作质量为m,半径为R的均质圆盘,设均质绳的质量为m0,绳总长度为L,滑轮转动时受轴承摩擦力矩为M。[6]两侧绳端下悬重物,释放重物后滑轮角加速度为α(逆时针),且设此瞬间滑轮左侧绳比右侧绳长l。
选择滑轮和绳组成的质点系作为研究对象,建立直角坐标系Oxyz。整个质点系对z轴的角动量分为滑轮和绳的两部分,其中,滑轮对z轴的角动量为:

设绳的一质元mi,它对z的角动量为mivR,故绳对z轴的角动量为:
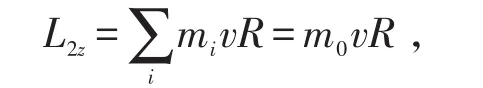
因绳与轮间无相对滑动,故:
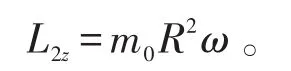
质点系总角动量为
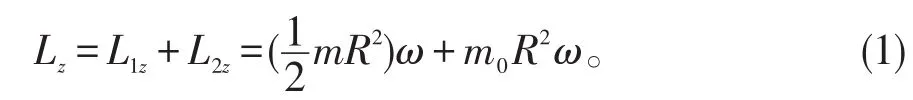

图1 定滑轮结构图
2 定滑轮两侧绳内张力差
质点系受力分析如图2,因滑轮两侧绳的对称部分所受重力对z轴的合力矩为零,故只有左侧多余部分绳所受的重力会产生力矩。考虑到α表示角加速度。
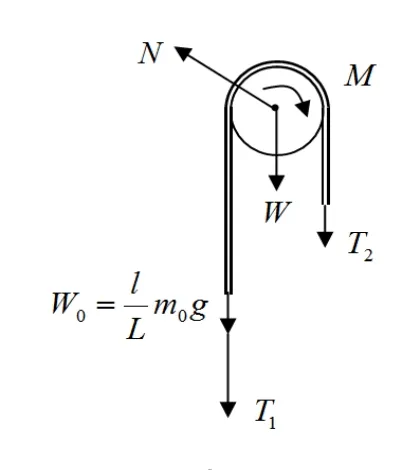
图2 质点系受力图
根据质点系角动量定理,有:

于是,绳两端的张力差为:

由(2)式可知,定滑轮两端存在张力差,与滑轮、绳的质量,以及轴承摩擦力矩都有关系。如果滑轮是“理想”的,绳与滑轮的质量不计,轴承摩擦不计,绳不伸长。即m,m0,M都忽略不计,则滑轮两侧的张力相等。
3 定滑轮转动时的摩擦力
根据上述计算结果,如果不考虑绳的质量和轴承摩擦力矩,而滑轮的质量不能忽略,那么绳子两端的张力差为:


图3 绳子受力图
隔离分析滑轮的受力情况就会知道,轮缘和绳子之间一定存在静摩擦力,并且正是这个力在促使滑轮加速转动。下面我们通过计算进行验证。
在绳子AB上假想地截取一段小弧,对应于平面角dθ,对其受力分析,T和T′为小弧两端的拉力,设T′=T+dT,f为静摩擦力,分别在切向列出动力学方程:
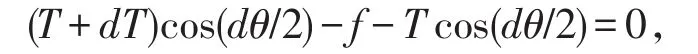
因dθ很 小 ,cos(dθ∕2)≈ 1 ,sin(dθ∕2)≈dθ∕2 ,dT-f=0,积分得,
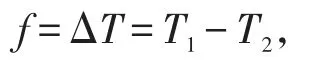
故,静摩擦力的对滑轮的力矩为:
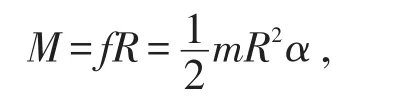
4 结论
定滑轮两侧绳内张力差与绳的质量、定滑轮的质量、轮的半径、轴摩擦力矩以及定滑轮转动时的角加速度大小都有关系。
根据计算结果可以看到:
(1)绳和滑轮的质量越大,张力差就越大;滑轮轴承的摩擦力越大,张力差越大;只有当绳和滑轮的质量极小,轴摩擦极小,则在这两个条件同时具备的极限情况下,滑轮两侧绳内张力趋于相等,这种极限情况即常提到的理想滑轮。除此以外,只要其中一个不能忽略不计,滑轮两侧的拉力就不相等。
(2)定滑轮两侧绳内张力差是不断变化的,即在不同的时刻有不同的取值,具体大小取决于两侧绳子长度的差,长度差越大张力差反而越小。
(3)绳子两侧的张力实际上并没有直接作用在滑轮上,彼此之间是始终存在着静摩擦力,恰是这个静摩擦力既维持绳子相对于滑轮的相对静止,又在促使滑轮的加速转动。所以,理想滑轮忽略的是滑轮轴承的摩擦力,对于轮缘和绳子之间的静摩擦力是必须存在的。在只考虑滑轮重量的情况下,绳子和滑轮轮缘之间的静摩擦力的大小正好等于绳子两端的张力差。
[1]课程教材研究所.八年级上册物理[M].北京:人民教育出版社.2012:84.
[2]陈钢,晏世雷.质点系中阿特伍德机对有关定理的检验意义[J].物理与工程,2013,23(4):14-15.
[3]蔡厚贵.解析滑轮的转动[J].贵阳学院学报(自然科学版)(季刊),2011,6(3):13-17.
[4]杨毅.滑轮转动中的摩擦力做功问题[J].教育心地,2006(35):67.
[5]冀敏,蒋平.定滑轮中的力学原理[J].物理与工程,2016,26(3):9-11.
[6]漆安慎,杜婵英.力学[M].2版.北京:高等教育出版社,2005.
〔责任编辑 高彩云〕
Analysis of the Tension Difference between the Ropes on Both Sides of the Fixed Pulley and the Friction Force
GAO Cai-yun
(School of Physics and Electronic Science,Shanxi Datong University,Datong Shanxi,037009)
The particle system composed of fixed pulley and rope is chosen as the object of study.According to the angular mo⁃mentum theorem of the particle system,the tension difference between the ropes on both sides of the fixed pulley is calculated,and the condition that the quality of the fixed pulley can not be neglected is analyzed.The results show that the tension between the two sides of the pulley is related to the quality of the rope and pulley,the radius of the wheel,the friction moment of the shaft,and the angular accel⁃eration of the pulley.In the extreme case,the tension between the two sides of the pulley tends to be equal.The static friction between the flange of the fixed pulley and the rope causes the pulley to rotate rapidly.
tension;angular momentum;friction;torque;fixed pulley
O313.3
A
1674-0874(2017)05-0022-03
2016-11-15
高彩云(1980-),女,山西五台人,硕士,讲师,研究方向:物理教育。
