生猪养殖场经营管理的线性规划模型

董建新，朱 帅

（1.长治学院数学系，山西长治046011；2.山西大同大学数学与计算机科学学院，山西大同037009）

生猪养殖场经营管理的线性规划模型

董建新1，朱 帅2

（1.长治学院数学系，山西长治046011；2.山西大同大学数学与计算机科学学院，山西大同037009）

以全国大学生数学建模竞赛题目为研究背景，建立了生猪养殖场经营管理的三个线性规划模型：首先是在养猪场的规模达到饱和时,每头母猪每胎的平均产仔量和成活仔数的模型；其次是在饱和状态下，肉猪与种猪的比例和母猪存栏数使盈利最大的模型；最后是猪仔长成肉猪后的3年里，每个月母猪与肉猪存栏数的模型。通过数学软件计算求解，得出养猪场在各种情况下的最佳经营策略。

生猪养殖；数学模型；数学软件；线性规划

1 问题分析

以2014年全国大学生数学建模竞赛C题为研究背景。

根据题目要求，分析得出三个问题：

（1）假设生猪养殖成本及生猪价格保持不变，且在不出售猪苗的情况下，小猪全部转化为种猪与肉猪，以此来建立模型，计算出每头母猪的平均产仔量;

（2）以养殖规模达到饱和状态为条件，目标函数为盈利最大建立线性规划，求解出肉猪与种猪的比例，及母猪的存栏数;

（3）根据给出的三年内生猪价格变化的预测，建立该养猪场的最佳经营策略模型，即母猪及肉猪存栏数，同时计算出三年内的平均年利润。

2 模型假设

(1)假设养殖场中的猪不受疾病灾害，自然灾害的影响，成长期间是自然的生老病死。

(2)在第一、二问中，肉猪卖出的价格假定不随时间的变化而变化。

(3)一般来说公猪与母猪自然交配的比例一般在1∶15～1∶25之间，所以在整个模型当中假设公猪：母猪=1∶20。

3 符号说明

R0：养殖场原有的乳猪数量；

Rj(i)：第i个月中月龄为j月的肉猪数；

K：每胎成活猪数；

Z（ji）：第i个月中月龄为j月的种猪数；

m:1：肉猪与种猪的比例；

F(i)：第i个月的收益；

f(i)：第i个月消费；

a：饲料的价格。

4 模型建立与求解

4.1 模型1

因为母猪配种到所产的猪仔长成肉猪出栏需要约9个月的时间，公猪与母猪配种后需要4个月的时间产下乳猪，乳猪生长期间不用喂食饲料，大约1个月的时间长成小猪开始食用饲料，所以小猪长成肉猪与种猪的时间基本为4个月。因此，将猪的类别分为六种：乳猪(0月龄猪)、一月龄猪、二月龄猪、三月龄猪、四月龄猪、五月龄猪。

对于第i个月来说，本月的乳猪数量影响着第i+1月的一月龄猪数量，本月的一月龄猪数量影响着第i+1月的二月龄猪的数量，…，以此类推我们找出生长了各月龄的猪与最初乳猪R0的关系。

又因为各个阶段的猪所吃的猪饲料不同，且肉猪与母猪所吃的猪饲料也不同，根据实际情况，这里设的猪消费猪饲料为0.8·a，的猪消费猪饲料为a,Z2(i)、Z3(i)的猪消费猪饲料0.9a，Z4(i)、Z5(i)的猪消费猪饲料1.2a。

通过分析，建立如下数学模型：

%月龄为5月的种猪数量来自上个月月龄为4月的猪以及上个月本身的数量。

%月龄为2,3,4月的种猪都来自前一个月份的数量。

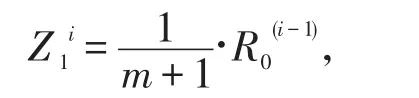
%月龄为1月的种猪来自于乳猪的部分。

%乳猪来自于月龄为5月的母猪所产的仔数。

%月龄为1月的猪来自于乳猪的部分。

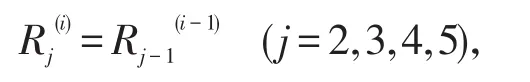
%月龄为2,3,4,5月的猪来自于前一个月龄的猪。

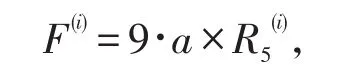
%第i个月收益。

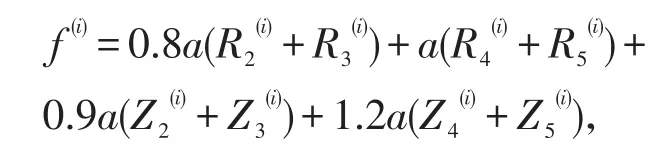
%第i个月饲料消耗。

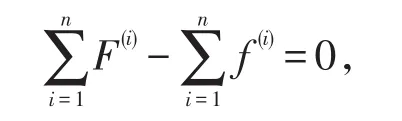
%达到平衡点。

应用MATLAB软件求解，在进行原始数据输入时，对数据合理性假设。假设肉猪5个月龄段的头数相同，即R1=R2=R3=R4=R5=100,种猪5个月龄段的头数也相同，即Z1=Z2=Z3=Z4=Z5=20,a=100，m=100。改变每胎成活仔数K的值，得出对应的Z5、R0以及i，从而可计算出对应的每头母猪每年平均产仔量要达到的值等于具体结果见表1：

表1 每胎成活仔数与平均产仔率的对应关系

再利用曲线拟合，找出K与每头母猪每年平均产仔量的动态关系，如图1：

图1 每胎成活仔数与平均产仔率的关系

得出：在达到盈亏平衡点的条件下，每头母猪每胎成活仔数与每头母猪每年平均产仔量的关系呈二次多项式，即：K=-0.0112x2+1.7487x-4.7458

4.2 模型2

题目要求养殖场养殖规模要达到饱和10000头猪，即在达到临界点之前，小猪不应出售为猪苗。因此在模型二只考虑从不饱和到饱和这段期间，肉猪与种猪的变化情况直至达到稳定状态的分配比例。

建立线性规划模型，约束条件是：在第1月时（刚饱和时），肉猪Rj与种猪Zj的总和为10000；第i个月时，肉猪Rj与种猪Zj的总和仍为10000。在计算时将第一个月时的各月龄肉猪和种猪的头数作为基础数据，第i个月时各月龄肉猪和种猪的头数均可在模型一当中找到它们与基础数据联系，这样在整个线性规划当中只有未知量R0,R1,R2,R3,R4,R5,Z1，Z2，Z3，Z4，Z5，目标函数是盈利最大。因此，建立模型如下：

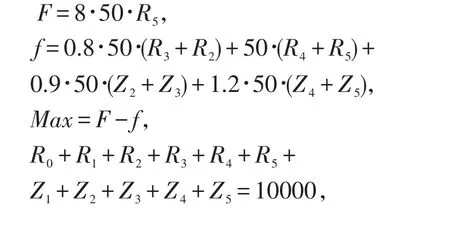
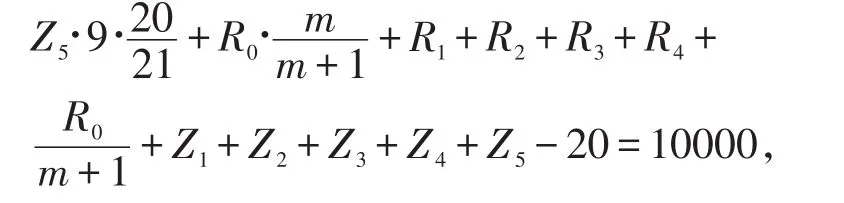
利用数学软件LINGO程序，求解得m=34，即小猪选为种猪的比例为肉猪:种猪=34∶1，母猪的存栏数为353。

4.3 模型3

题目给出了养猪场9月后3年内生猪价格变化曲线，即在这36月内，每月都对应一个生猪价格，为简化模型，假设价格为该月30天的生猪价格，肉猪与乳猪价格之比为1∶2，这样就列出肉猪与乳猪的价格表，见表2。

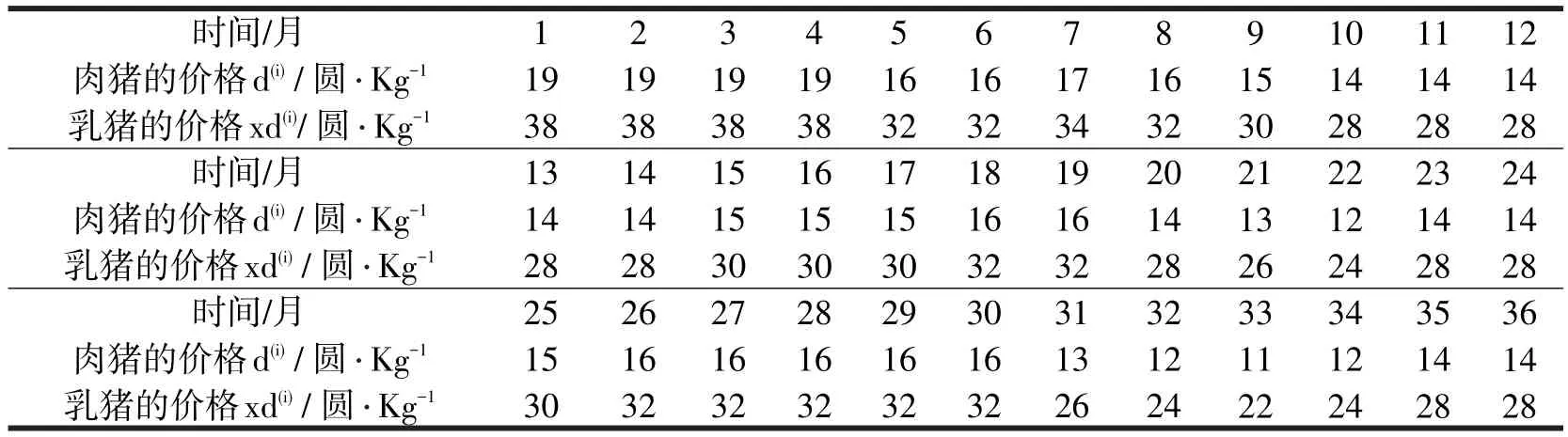
表2 肉猪与乳猪每个月份的价格

表3 各月龄猪的变化情况

根据给出的数据建立规划模型：

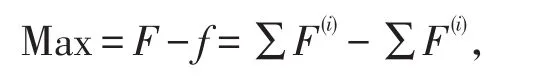
%目标函数为收益最大，

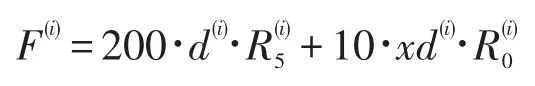
%第i个月收益，

%第i个月饲料消耗，

%猪厂规模约束，

%以上为各月龄猪的变化情况约束。

利用LINGO软件求解模型，可得出最大的利益及各月龄猪的变化情况，见表3。

从而可以求得：三年的平均年利润为3948000元，以及在此策略下的母猪及肉猪存栏数，如表4。

本模型充分利用数学软件进行编程求解，通俗易懂，在一定条件下给出生猪养殖的经营策略[1-3]，即要想达到盈利最大化，猪苗、肉猪、种猪等的存栏数分配。

表4 母猪及肉猪存栏数

[1]姜启源,谢金星,叶俊.数学模型[M].4版.北京:高等教育出版社,2011.

[2]孙海梅.生猪出栏率计算方法的进一步完善[J].四川畜牧兽医.2000，30(6):29-30.

[3]刘志伟,陈义锋,王关梅.农户生猪养殖规模的数学模型[J].贺州学院学报.2014,30(3):130-135.

〔责任编辑 高海〕

The Linear Programming Model for the Management Strategy of Pig Farms

DONG Jian-xin1,ZHU Shuai2
（1.Department of Mathematics,Changzhi University,Changzhi Shanxi,046011；2.School of Mathematics and Computer Science,Datong University,Datong Shanxi,037009)

Based on the background of the CUMCM topic,three linear programming models for the management of pig farms were established.First,the model of the average litter size and the number of larvae per litter of each sow was established when the size of the pig farm was saturated;Second,in the saturated state,the most profitable model was established,so that the ratio of pigs to pigs and the number of sows were calculated;Finally,in the three years after the pig grows into the pig,the model of the number of sows and pig⁃lets per month was established.By using mathematical software to solve the problem,we can get the best management strategy of pig farm under different circumstances.

pig breeding;mathematical model;mathematical software;linear programming

O29

A

1674-0874(2017)05-0018-04

2017-07-15

长治学院教研项目[JY201601]

董建新(1978-)，男，山西阳城人，硕士，讲师，研究方向：运筹优化与数值计算。