一类不确定混沌系统的自适应神经网络终端滑模同步控制
2017-12-02李媛,刘恒
李 媛,刘 恒
(1.山西传媒学院传媒管理系,山西晋中030619;2.淮南师范学院应用数学系,安徽淮南232038)
一类不确定混沌系统的自适应神经网络终端滑模同步控制
李 媛1,刘 恒2
(1.山西传媒学院传媒管理系,山西晋中030619;2.淮南师范学院应用数学系,安徽淮南232038)
研究了不确定混沌系统自适应神经网络终端滑模同步控制器的设计问题。使用神经网络系统估计系统的不确定项。设计的终端滑模面可以保证同步误差在有限时间内稳定。基于Lyapunov稳定性理论证明了误差动态系统的稳定性。仿真实验的结果表明该方法有较好的同步控制效果。
混沌系统;终端滑模控制;自适应神经网络控制
近年来,混沌系统的同步及控制在保密通信、信号加密中得到广泛的应用,逐渐成为研究热点。混沌同步主要是设计合适的控制器,使从系统信号跟踪主系统信号且同步误差满足一定的要求。截止到目前,很多控制方法被用来实现两混沌系统的同步,如线性反馈控制[1-2],自适应控制[3-5],主动控制[3],脉冲控制[6-7],间歇控制[8-9],反步控制[10]等。需要注意的是,上述方法只能针对混沌系统的模型完全已知或者至少部分已知的情况。所以,对系统模型完全未知的混沌系统的同步控制问题值得研究。
众所周知,滑模控制是处理不确定非线性系统的控制问题的一种常用方法[11]。需要指出的是文献[12]提出了终端滑模控制方法来实现非线性系统的有限时间控制。该控制方法主要使用的是非线性的滑模面。受文献[3,11]启发,本文主要研究不确定混沌系统的同步问题。采用的方法是自适应神经网络和终端滑模控制相结合的控制方法。首先,设计了一种积分终端滑模面;然后基于Lyapunov稳定性理论设计自适应神经网络控制器。本文的创新性主要可以总结为:(1)与传统的滑模面比较,本文提出的终端滑模面容易构造且具有较好的连续性;(2)控制器的设计中不需要系统模型的先验知识。
1 问题描述和基础知识
考虑如下的主系统和从系统:
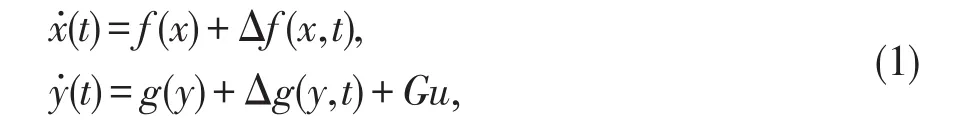
其中x∈Rn和y∈Rn为系统状态向量,f∈Rn,g∈Rn为连续的非线性函数。Δf∈Rn,Δg∈Rn为系统的不确定项,G∈Rn×Rn为可逆的控制增益矩阵。本文的控制目标是设计适当的控制器u(t)实现主系统和从系统的同步。
为了处理系统的未知项,我们需要用到神经网络。
其数学模型可描述为:

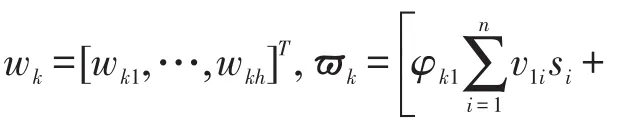

2 主要结果
定义同步误差为e=y-x。于是有
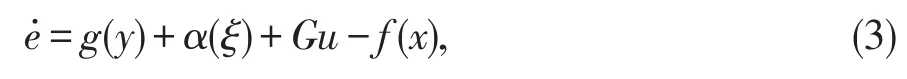
其中ξ=[xT,yT],α(ξ)=Δg(y,t)-Δf(x,t)=
[α1(ξ),α2(ξ),…,αn(ξ)]T为未知函数。构造如下的滑模面:
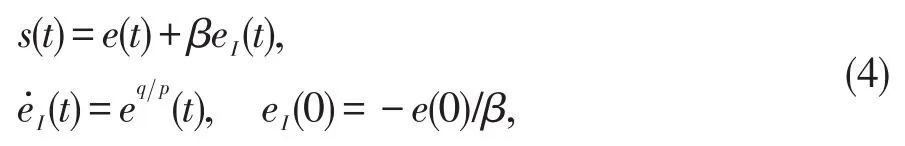
其中β>0;p,q满足p>q>0。根据公式(4)有公式(4)可改写为:
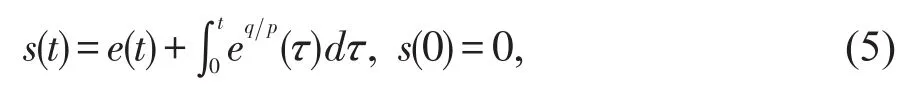
于是在滑模面s(t)=0上有

解微分方程(6)可得
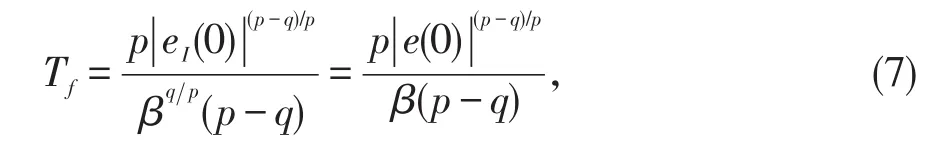
滑模面动态方程为

接下来,未知函数α(ξ)可以通过神经网络(2)估计为
设可调参数ϑi的最优估计为

定义参数的最优估计误差和未知函数的逼近误差分别为

如文献[12-13]中的方法类似,可以假设最优逼近误差有界,即存在大于零的常数i,i=1,2,…,n,使得于是
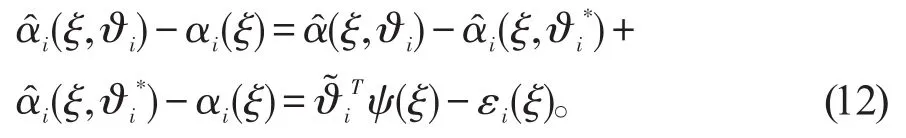
控制器可以设计为

根据上述讨论,有如下的结论:
定理1 考虑主混沌系统和从混沌系统(1)终端滑模面设计为(4)或其等价形式(5),控制器设计为(13),神经网络可调参数的自适应律定义为(14),于是可以得到同步误差e(t)和eI(t)的有限时间收敛性。
证明 定义Lyapunov函数为:
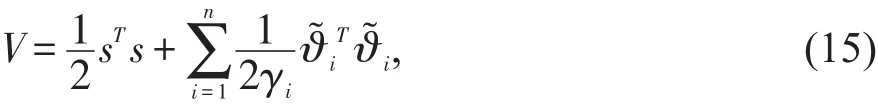
把控制器(13)带入动态方程(8)可得
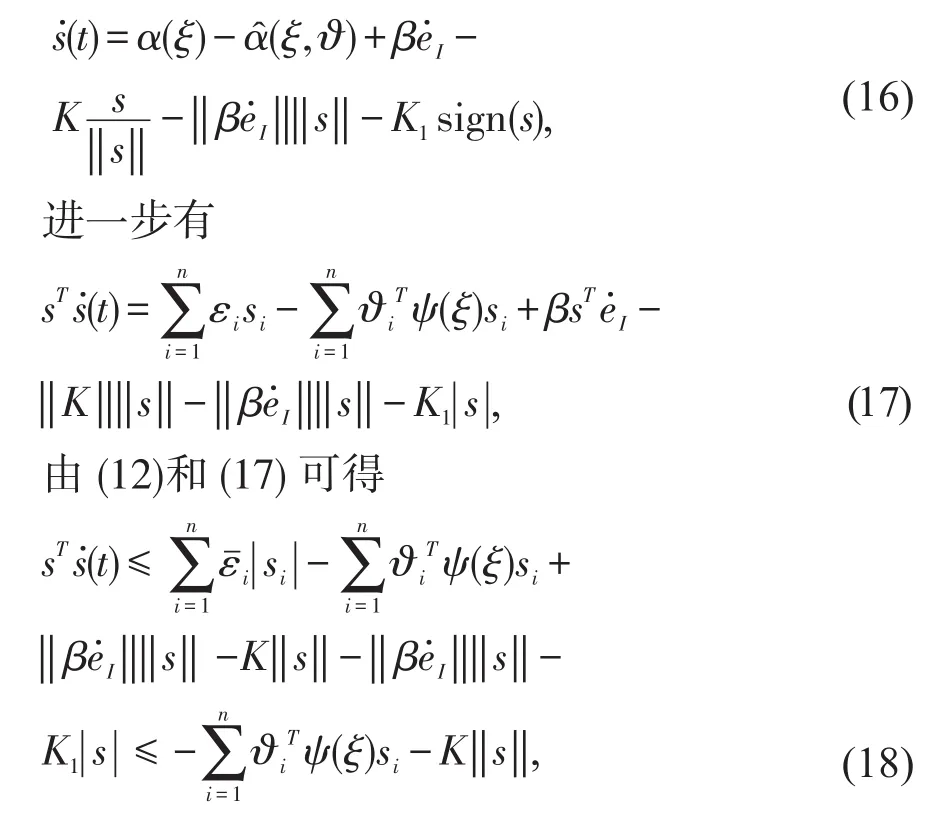
于是根据 (14),(15)和(18)有V˙≤ -‖K‖‖s‖。注意到s(0)=0,V˙<0,所以系统信号停留在s(t)=0。于是同屋误差e(t),eI(t)再有限时间内收敛到原点。证毕。
3 仿真研究
将利用3-D保护多涡卷混沌系统的同步控制问题验证本文方法的有效性。该多涡卷混沌系统可描述为:
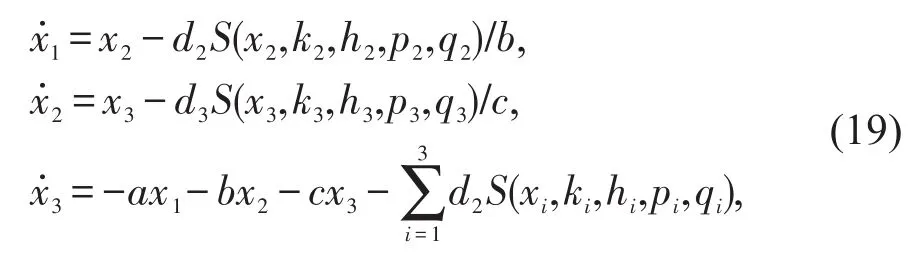
其中饱和函数序列S定义为
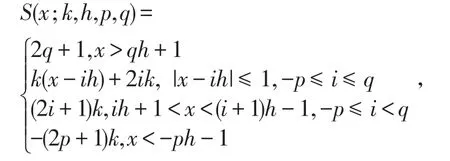
神经网络的控制输入为ξ。当参数a=d1=0.7,k1=100,h1=200,k2=k3=40,h2=h3=80,pi=qi=2,系统(19)为混沌系统,其混沌显现见图1。
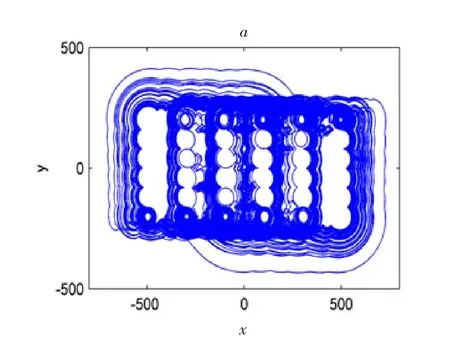

图1 系统(19)混沌吸引子(a):x-y平面,(b):x-z平面
仿真中,主系统的非线性函数
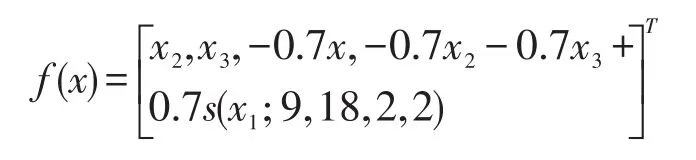
从系统的系统模型和主系统一致。控制增益矩阵选为G=I3×3。系统的初值为:

控制参数为k1i=k2i=1,γi=100,i=1,2,3。
同步结果见图2。从仿真结果可以看到,本文的控制方法取得了较好的同步效果。
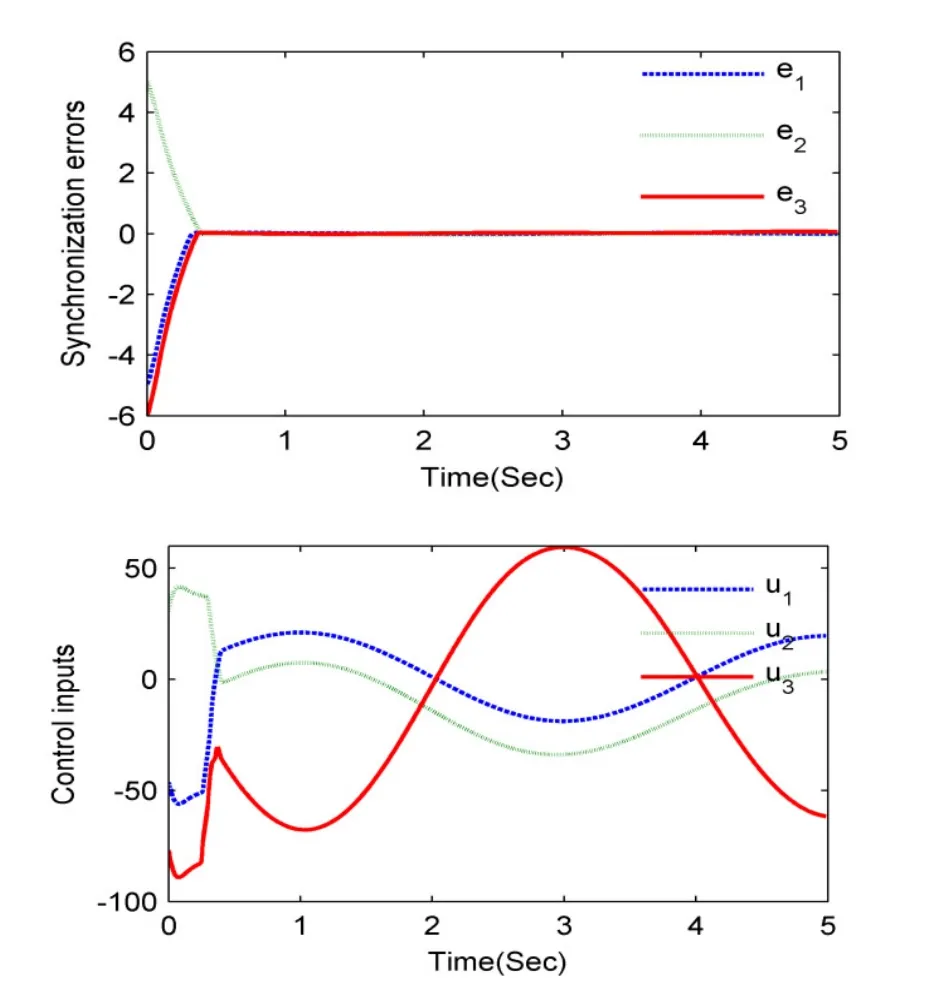
图2 同步误差
4 结论
①设计的终端积分滑模面有较好的连续性,可以实现同步误差的有限时间稳定;②系统状态向量一旦到达s=0将会保持这种状态;③设计的自适应神经网络控制器具有非常好的逼近性能,不需要系统模型的先验知识。
[1]He W,Cao J.Generalized synchronization of chaotic systems:an auxiliary system approach via matrix measure[J].Chaos,2009(19):013118.
[2]Utkin V I.Sliding mode control design principles and applications to electric drives[J].IEEE Transactions on Industrial Electron⁃ics,2008,40(1):23-26.
[3]Botmart T,Niamsup P,LIU X.Synchronization of non-autonomous chaotic systems with time-varying delay via delayed feedback control[J].Commun Nonlinear Sci Numer Simulat,2012(17):1894-1907.
[4]Botmart T,Niamsup P.Adaptive control and synchronization perturbed Chuas system[J].Math Comput Simulat,2007(35):37-55.
[5]Mahmoud G M,Ahmed M E,Abed-elhameed T M.Active control technique of fractional-order chaotic complex systems[J].The European Physical Journal Plus,2016,131(6):1-11.
[6]Xiong W,Huang J.Finite-time control and synchronization for memristor-based chaotic system via impulsive adaptive strategy[J].Advances in Difference Equations,2016(1):101.
[7]Zochowski M.Intermittent dynamical control[J].Phys.D,2000(145):181-190.
[8]Liu C,Yang Z,Sun D,etal.Synchronization of chaotic systems with time delays via periodically intermittent control[J].Journal of Circuits Systemsamp;Computers,2017,in press.
[9]Hu C,Yu J.Generalized intermittent control and its adaptive strategy on stabilization and synchronization of chaotic systems[J].Cha⁃os Solitonsamp;Fractals,2016(91):262-269.
[10]Chiu C S.Derivative and integral terminal sliding mode control for a class of MIMO nonlinear systems[J].Automatica,2012(48):316-326.
[11]Liu H,Pan Y,Li S,etal.Synchronization for fractional-order neural networks with full∕under-actuation using fractional-order slid⁃ing mode control[J].International Journal of Machine Learningamp;Cybernetics,2017:1-14.
[12]刘恒,李生刚,孙业国,等.带有未知非对称控制增益的不确定分数阶混沌系统自适应模糊同步控制[J].物理学报,2015,64(7):070503.
[13]Bartolini G,Ferrara A,USAI E,etal.On multi-input chattering-free second-order sliding mode control[J].IEEE Transactions on Automatic Control,2000,45(9):1711-1717.
[14]Lü j,Murali K,Sinha S.Generating multi-scroll chaotic attractors by thresholding[J].Physics Letters A,2008(372):3234-3239.
〔责任编辑 高海〕
Adaptive Neural Network Terminal Sliding Mode Synchronization for a Class of Uncertain Chaotic Systems
LI Yuan1,LIU Heng2
(1.Department of Media Management,Communication University of Shanxi,Jinzhong Shanxi,030619;2.Department of Applied Mathematics,Huainan Normal University,Huainan Anhui,232038;)
In this paper,synchronizing two different chaotic systems with system uncertainties is addressed by means of adaptive neural network integral terminal sliding mode control.The controller can guarantee the fast convergence of the synchronization error in some finite time and the singular problem in traditional sliding mode control can also be avoided.Finally simulation studies are carried out to show the effectiveness of the proposed method.
chaotic system;terminal sliding mode control;adaptive neural network control
TP273
A
1674-0874(2017)05-0008-04
2017-03-26
李媛(1981-),女,山西太原人,硕士,讲师,研究方向:非线性系统及分数阶非线性系统控制和仿真。
