饱和输入限制下欠驱动自主水下航行器水平面航迹跟踪控制
2017-12-01江梦洁李家旺吕艳芳周家炜黄汉涛
江梦洁, 李家旺, 吕艳芳, 周家炜, 黄汉涛
(宁波大学 海运学院, 浙江 宁波 315211)
饱和输入限制下欠驱动自主水下航行器水平面航迹跟踪控制
江梦洁, 李家旺, 吕艳芳, 周家炜, 黄汉涛
(宁波大学 海运学院, 浙江 宁波 315211)
针对控制输入存在饱和限制的欠驱动自主水下航行器水平面航迹跟踪问题,提出了一种饱和控制方法。在航迹跟踪误差方程基础上,设计了一种误差信号观测器对原有跟踪误差进行近似,以避免由于跟踪误差直接求导所引起的控制器表达式的复杂化现象;推导得到一种新的误差动力学方程,通过引入一种光滑有界函数作为输入饱和条件的近似,以及一种Nussbaum型偶函数,设计了饱和动力学控制器;根据Lyapunov理论证明了该控制器能够使得自主水下航行器在控制输入饱和限制下,可以实现对任意光滑水平面航迹的跟踪控制,并保证跟踪误差是全局最终一致有界的。仿真实验结果验证了该设计方法是有效的,且对于模型参数误差具有一定的鲁棒性。
控制科学与技术; 欠驱动自主水下航行器; 输入饱和; 跟踪控制; 误差观测器; Nussbaum型函数
0 引言
自主水下航行器(AUV)已经成为重要的军用和民用海洋装备之一。AUV的平面跟踪自动控制问题也一直是控制领域的研究热点之一。对于这类问题,其难点主要在于AUV具有明显的欠驱动特性,即在某些自由度上不存在有效输入。目前,国内外的研究人员针对该类问题已经获得了很多研究成果。在这些研究成果中,根据平面参考轨迹生成方式的不同,主要分为两类:轨迹跟踪和航迹跟踪。在轨迹跟踪问题中,参考轨迹由“虚拟模型”产生,该模型具有和真实的AUV相同的动力学特性,可以同时实现AUV位置和方向角的跟踪[1-4],但参考轨迹的形式存在很多限制,且难以提前设定,因此在实际应用时存在很大的局限性。与之不同,在航迹跟踪问题中,仅要求AUV实现位置跟踪,使得参考轨迹可以是提前设定的任意平面曲线或一系列航迹点,因此其更能体现实际中AUV的跟踪需求[5-10]。
需要指出的是,上述研究成果均未考虑控制输入的饱和限制问题,因此,所设计的控制方法在实际应用中可能无法达到预期的控制性能。为此,文献[11]研究了存在速度和输入饱和限制的欠驱动船舶的航迹跟踪问题,但其未考虑建模误差与环境干扰的影响。文献[12]针对某型存在输入饱和限制的AUV,提出了一种基于线性矩阵不等式(LMI)方法的水平面路点跟踪策略,但其仅能保证跟踪误差的局部稳定性。文献[13]基于多层神经网络和自适应鲁棒控制方法设计了一种航迹跟踪控制器以降低建模误差和环境干扰的不利影响,但其控制器形式较为复杂,且并未从严格意义上证明误差系统的稳定性。
在上述研究基础上,本文针对带有饱和控制输入的欠驱动AUV的水平面航迹跟踪问题进行了研究。主要工作和创新点包括:1) 基于跟踪误差方程,提出了一种误差观测器模型,并以观测值作为新的控制对象,建立了新的误差动力学方程,从而避免了由于对原始跟踪误差信号的直接求导所引起的控制器“膨胀”现象;2) 通过引入一种Nussbaum型偶函数,设计了欠驱动AUV的航迹跟踪饱和控制器,使得AUV的控制输入能够在不触发饱和情况下,实现对参考航迹的跟踪。最后通过数值仿真方式对所设计的控制器的有效性和鲁棒性进行了验证。
1 AUV数学模型及问题描述
1.1 AUV水平面运动模型
AUV水平面航迹跟踪问题的示意图及相关坐标系定义如图1所示。
在图1中:Oxy表示地面坐标系;BxByB表示随体坐标系,其中点B一般取在AUV的质心或浮心处;Γ表示参考航迹;(xd,yd)表示当前参考航迹点在Oxy中的坐标。
假设AUV具有轴对称外形,质量均布,且升沉、纵摇和横滚等运动的影响可忽略不计,则AUV的3自由度水平面运动方程[14]可表示为
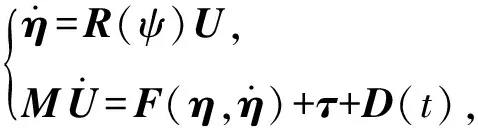
(1)
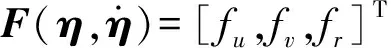
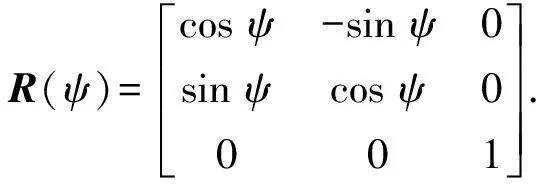
(2)
由(1)式可以看出,AUV在ByB轴方向上不存在控制输入,因此该AUV是欠驱动的。
在实际情况下,由于AUV的控制输入始终是有限的,因此(1)式中的τ必然存在饱和限制,即
τi=sat(τi)=sgn (τi)min (|τi|,τimax),i=u,r,
(3)
式中:sat(·)表示饱和函数;sgn(·)表示标准符号函数;τumax和τrmax分别表示对应输入的最大值。
此外,由实际情况可知(1)式中的干扰项D(t)也是始终有界的。为了方便控制设计,对其作出以下假设。
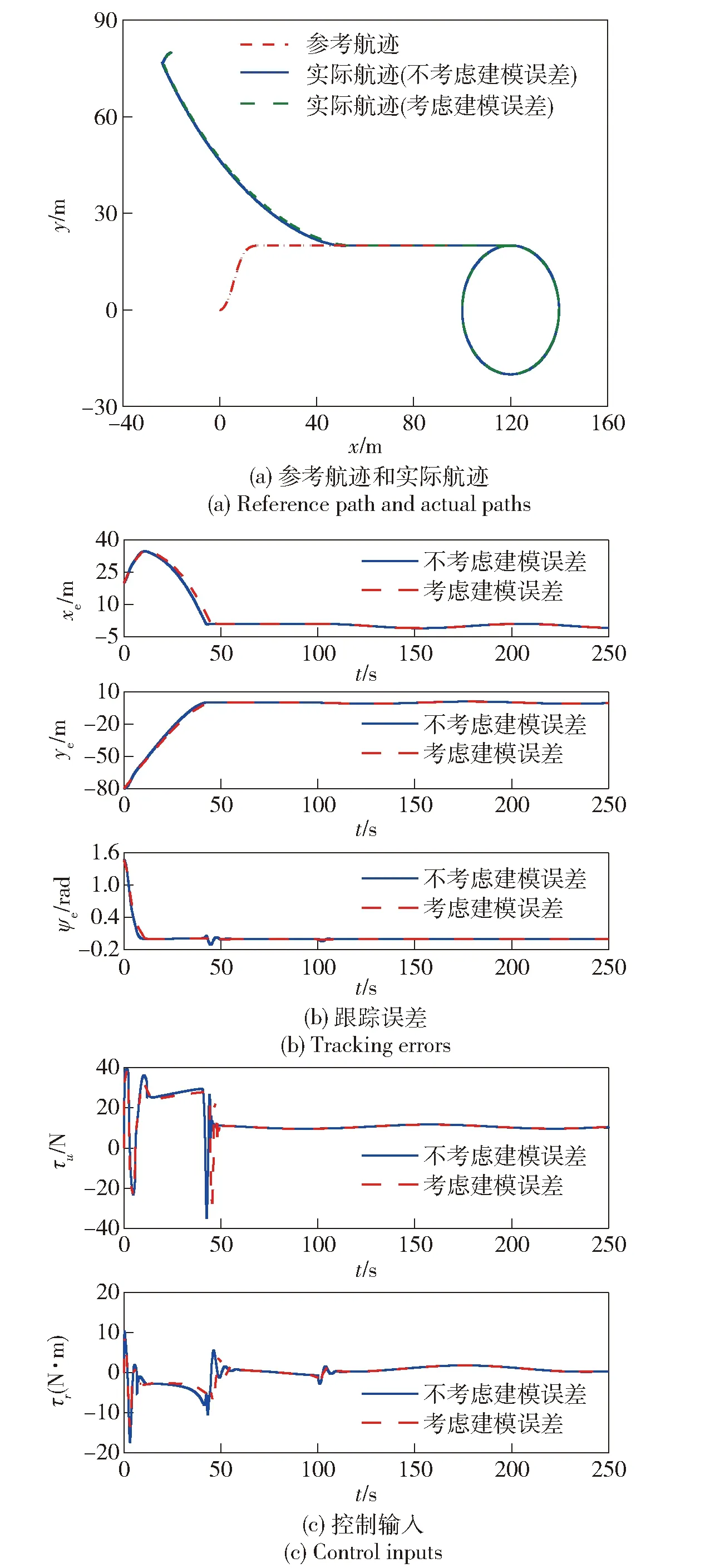
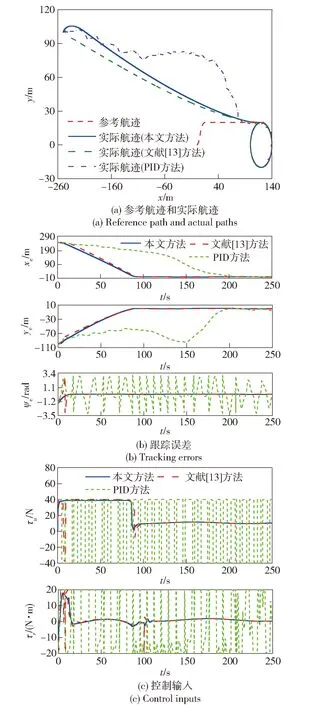
假设1:环境干扰D(t)满足|du| 不仅如此,将假设1和(3)式代入(1)式的第2个方程中,通过分析也不难得到,AUV的速度向量U必然是有界的。 此外,考虑到在实际情况下,AUV需要跟踪的参考航迹随时间的变化率应为有限值,因此下面对参考航迹(xd,yd)做出限制。 1.2 问题描述 本文所研究的控制问题可描述为:针对由(1)式表示的AUV水平面运动模型,对于给定的任意一条光滑的参考平面航迹(xd,yd),在由(3)式表示的输入饱和限制条件下,通过设计螺旋桨推力τu和舵转矩τr,使得跟踪误差(xd-x,yd-y)收敛到原点附近一个有界的邻域内。 为此,定义以下跟踪误差变量: (4) 式中:xe=xd-x;ye=yd-y;ψd表示AUV相对于参考坐标点的视线角,具体定义为 ψd=0.5π[1-sgn (xe)]sgn (ye)+arctan (ye/xe), (5) 由(5)式可知ψd∈[-π,π)。 对(4)式求导,可得跟踪误差方程如下: (6) 式中:ξ=[e,ψe]T;U1=[u,r]T;H=diag{cosψe,1};E=[Ee,Eψ]T,Ee和Eψ分别为 (7) 由(6)式不难得知,上述跟踪控制问题等价于下述镇定控制问题,即:通过设计τu和τr,使得跟踪误差变量(e,ψe)收敛到原点附近的有界邻域内。 针对跟踪误差方程式(6)式,常用的控制方法包括反步法[9]和滑模控制法[10]等。但这些控制方法都需要对(6)式进行直接求导,这不仅增加了设计难度,也会使得最终的控制器形式较为复杂而难以应用。为此,本节中将给出一种控制设计方法以避免上述不足。该方法包含两个部分:1)设计误差观测模型对(6)式进行近似,以避免在后续设计中对其直接求导,从而避免出现控制器表达式“膨胀”现象;2) 根据跟踪误差变量的观测值,定义新的误差向量,并在此基础上设计饱和动力学控制器,以使得跟踪误差能够收敛至零点附近的有界区域内。 2.1 基于观测估计的跟踪误差模型 针对(6)式,设计以下误差信号观测器: (8) (9) 其中λH和λE都是正常数。 根据(6)式和(8)式,可知观测误差满足: (10) (11) 经过简单分析不难得知: (12) 2.2 饱和控制器设计 (13) 式中:kξ>0;e=-δ,δ=[δ0,0]T表示期望的稳态跟踪误差,δ0≥0. 对(13)式求导,并结合(1)式、(6)式、(8)式和(9)式,可得新的跟踪误差方程为 (14) 考虑到τu和τr满足(3)式,为了方便设计,定义以下光滑有界函数作为(3)式的近似: (15) 针对(14)式,为了镇定新的误差向量ξm,选择控制输入信号τu和τr如下: (16) (17) 式中:kχi和λχi均为正常数。 将(15)式~(17)式代入(14)式,可得跟踪误差方程为 (18) 以及控制误差方程为 (19) (20) 根据假设2,结合(7)式、(9)式和(12)式,利用Young不等式ab≤ϑa2/2+b2/2ϑ,∀a,b≥0,∀ϑ>0,(20)式可简化为 (21) (22) 式中:χi0=χi(0);χit=χi(t). 由(22)式可知,当χit有界时,V(t)也是有界的。因此,为了证明V(t)的有界性,仅需证明χit是有界的。下面采用反证法进行证明。 (23) 综上可知,χit是有界的,因此V(t)也是有界的。而根据V(t)和X(t)之间关系,可知X(t)是有界的,进而可知e,i、ξm,i和都是有界的。根据e,i定义,考虑到δ为常向量,因此i是有界的,而根据2.1节中相关结果可知,跟踪误差ξ也会收敛至零点附近的一个有界区域内。 为了验证上述控制方法的性能,以文献[10]中的“REMUS”AUV模型为对象进行了相关仿真实验。该AUV模型的动力学方程为 (24) 式中:模型参数为mu=31.41 kg,mv=65.98 kg,mr=38.95 kg·m2,Xu=8.806 5 kg/s,Yv=65.545 7 kg/s,Nr=6.735 2 kg·m2·s;干扰项设定为du=sin (0.05t),dv=cos (0.05t),dr=0.5sin (0.05t). AUV的初始状态设定为η(0)=[-20,80,-8π/9]T,U(0)=[0,0,0]T. 控制输入的最大值为τumax=40 N和τrmax=20 N·s. AUV的参考水平面路径设定为 (25) 控制参数设定为λξ=5,λH=1.5,λE=0.5,kξ=2,δ0=1,θ=0.9,kα=2,kζu=kζr=5,λα=15,λ0=100,ku=kr=20,dumax=drmax=10,λχu=λχr=0.1,kχu=107和kχr=104. 仿真结果如图2所示。 图2 AUV水平面航迹跟踪仿真结果Fig.2 Simulated results of path tracking of AUVs on horizontal plane 由图2可以看出,所设计的控制器能够使得AUV在较短的时间内跟踪上参考航迹,并保证稳态跟踪误差始终保持在零点附近的一个小范围内。另外,在整个控制过程中,螺旋桨推力的最大值约为39.36 N,舵转矩最大值约为7.33 N·m,都未触发饱和现象。 考虑到在实际情况下,AUV模型参数可能存在一定的误差,图2中还给出了AUV模型存在建模误差时的跟踪仿真结果。其中,相关模型参数名义值取为mu0=0.5mu,mv0=0.7mv,mr0=1.4mr,Xu0=0.5Xu,Yv0=0.7Yv,Nr0=1.5Nr. 控制参数同前。由图2可以看出,无论建模误差存在与否,控制器均具有一致的稳态跟踪精度,且误差收敛时间与控制输入大小都十分接近,证明了所设计的控制器对于AUV建模误差具有良好的鲁棒性。 此外,为了进一步验证本文控制器的性能,对存在较大初始位置误差条件下的AUV水平面航迹跟踪问题进行了数值仿真实验,并分别与经典PID方法和文献[13]中方法做了对比,其中AUV的初始状态设定为η(0)=[-250,100,π/3]T,U(0)=[0,0,0]T. 相关控制器参数的选择满足最佳控制性能要求,具体仿真结果如图3所示。 图3 较大初始误差下的AUV水平面航迹跟踪控制仿真对比Fig.3 Simulated results of path tracking of AUVs on horizontal plane with large initial tracking errors 由图3可知,当存在较大初始误差时,本文的控制方法与文献[13]中方法均实现了对参考航迹的跟踪,且跟踪误差收敛时间与稳态跟踪误差均十分接近。而PID方法仅在控制过程后段实现了对参考航迹的跟踪,但稳态位置跟踪误差较大,且角度跟踪误差并未收敛。另外,在这3种控制方法中,文献[13]方法与PID方法均触发了控制器饱和现象,而本文的控制方法所产生的螺旋桨推力的最大值约为38.79 N,舵转矩最大值约为17.9 N·m,都未触发饱和现象。因此,本文的控制方法具有更好的综合控制性能。 本文对带有饱和输入限制条件的欠驱动AUV的水平面航迹跟踪控制问题进行了研究。针对位置和角度跟踪误差信号,设计了一种误差观测器,以避免由于对原始误差信号直接求导所引发的控制器表达式“膨胀”现象。在此基础上,建立了一种新的误差动力学方程,针对该方程,考虑到控制输入的饱和限制条件,通过引入一种Nussbaum型函数,设计了相应的饱和控制器,可使得AUV的水平面航迹跟踪误差最终收敛至零点附近的一个有界区域内。仿真实验证明了所提出的方法是有效的,且对于建模误差具有良好的鲁棒性。此外,通过与现有控制方法的对比,也证明了本文方法具有更好的跟踪精度与抗饱和性。后续的进一步工作包括将本文中的控制方法拓展至AUV的三维空间航迹跟踪问题以及相关的模型试验研究等。 References) [1] Do K D, Jiang Z P, Nijmeijer H. Global output feedback universal controller for stabilization and tracking of underactuated ODIN-an underwater vehicle [C]∥Proceedings of the 41st IEEE Conference on Decision and Control. Las Vegas, NV, US: IEEE, 2002: 504-509. [2] Yan Z P, Yu H M, Zhang W, et al. Globally finite-time stable tracking control of underactuated UUVs [J]. Ocean Engineering, 2015, 107(1): 132-146. [3] Dong Z, Wan L, Liu T, et al. Horizontal-plane trajectory- tracking control of an underactuated unmanned marine vehicle in the presence of ocean currents [J]. International Journal of Advanced Robotic Systems, 2016, 83(13): 1-14. [4] Repoulias F, Papadopoulos E. Planar trajectory planning and tracking control design for underactuated AUVs [J]. Ocean Engineering, 2007, 34(11/12): 1650-1667. [5] Aguiar A P, Pascoal A M. Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents [J]. International Journal of Control, 2007, 80(7): 1092-1108. [6] Do K D. Practical control of underactuated ships [J]. Ocean Engineering, 2010, 37(13): 1111-1119. [7] Bi F Y, Wei Y J, Zhang J Z, et al. Position-tracking control of underactuated autonomous underwater vehicles in the presence of unknown ocean currents [J]. IET Control Theory and Applications, 2010, 4(11): 2369-2380. [8] 朱齐丹, 于瑞亭, 夏桂华, 等. 风浪流干扰及参数不确定欠驱动船舶航迹跟踪的滑模鲁棒控制[J]. 控制理论与应用, 2012, 29(7): 959-963. ZHU Qi-dan, YU Rui-ting, XIA Gui-hua, et al. Silding-mode robust tracking control for underactuated surface vessels with parameter uncertainties and external disturbances [J]. Control Theory & Applications, 2012, 29(7): 959-963.(in Chinese) [9] Li J H. Path tracking of underactuated ships with general form of dynamics [J]. International Journal of Control, 2016, 89(3): 506-517. [10] Elmokadem T, Zribi M, Youcef-Toumi K. Terminal sliding mode control for the trajectory tracking of underactuated autonomous underwater vehicles [J]. Ocean Engineering, 2017, 129(3): 613-625. [11] Chwa D. Global tracking control of underactuated ships with input and velocity constraints using dynamic surface control method [J]. IEEE Transactions on Control Systems Technology, 2011, 19(6): 1357-1370. [12] Kim D W. Tracking of REMUS autonomous underwater vehicles with actuator saturations [J]. Automatica, 2015, 58(1): 15-21. [13] Shojaei K. Neural adaptive robust control of underactuated marine surface vehicles with input saturation [J]. Applied Ocean Research, 2015, 53(2): 267-278. [14] Fossen T I. Marine control systems [M]. Norway: Marine Cybernetics, 2002. [15] Ge S S, Hong F, Lee T H, et al. Adaptive neural control of nonlinear of time-delay systems with unknown virtual control coefficients [C]∥Proceedings of the 41st IEEE Conference on Decision and Control. Las Vegas, NV, US: IEEE, 2002: 961-966. PathTrackingControlofUnderactuatedAutonomousUnderwaterVehiclesonHorizontalPlanewithinInputSaturationLimit JIANG Meng-jie, LI Jia-wang, LYU Yan-fang, ZHOU Jia-wei, HUANG Han-tao (Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, Zhejiang, China) A saturation controller is designed for the path tracking control of underactuated autonomous underwater vehicles (AUVs) on the horizontal plane within input saturation limitation. A first-order observer is designed to estimate the tracking errors to avoid complicating the controller expressions due to the direct derivation of tracking errors. An improved error dynamic model is derived. A saturated dynamic control strategy for the actual inputs is proposed by utilizing smooth bounded functions as the estimations of the saturated inputs and introducing a Nussbaum-type even function. The stability analysis via the Lyapunov’s theory shows that the proposed controller can achieve the tracking of arbitrary smooth paths of AUVs on horizontal plane within input saturation limit, and the tracking errors are globally ultimately uniformly bounded. Some simulated results are presented to illustrate the effectiveness and robustness of the proposed controller. control science and technology; underactuated AUV; input saturation; tracking control; error observer; Nussbaum-type function TP273+.2 A 1000-1093(2017)11-2207-07 10.3969/j.issn.1000-1093.2017.11.017 2017-05-08 国家自然科学基金项目(51309133) 李家旺(1981—), 男, 副教授, 硕士生导师。E-mail: lijiawang@nbu.edu.cn
2 控制设计

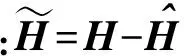
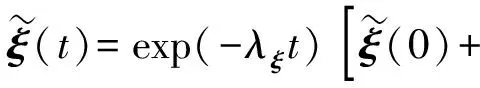
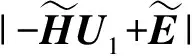

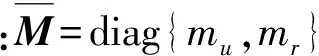
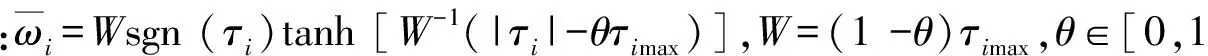
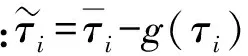
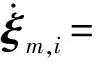
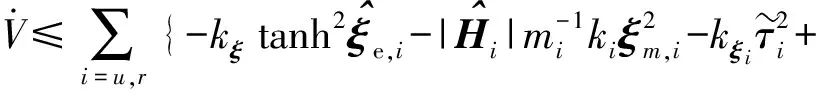
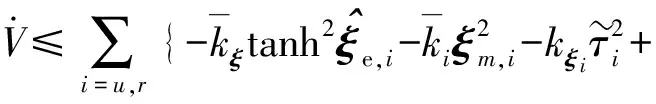
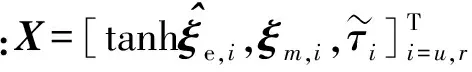


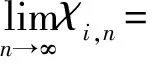
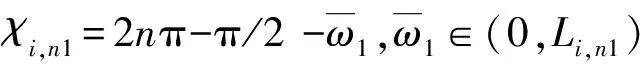
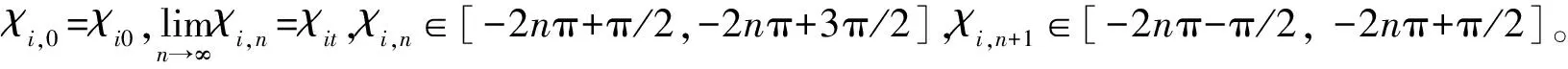
3 仿真实验
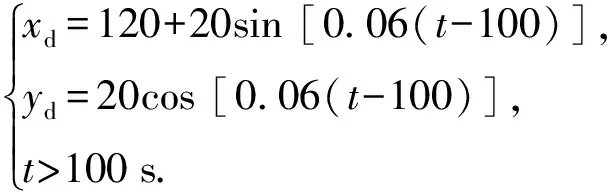
4 结论
