一种基于SOM的多维农业时空数据可视化分析方法

彭俊+卢艳松+夏凯

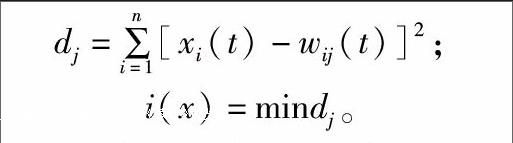
摘要：随着“3S”、物联网等技术逐渐被应用于农业生产过程中，多维农业时空数据大量产生。如何挖掘和分析多维时空数据在时空上的内在价值，对推动现代农业发展有重要意义。针对多维农业时空数据存在维数高，数据关系复杂，难以直接挖掘分析的问题，提出一种基于SOM的多维农业时空数据可视化分析方法。该方法利用SOM算法对多维数据降维，结合数据表、平行坐标系、时空立方体等可视化组件，实现数据的多角度显示和分析，达到深层次挖掘的目的。基于该方法，设计完成可视化分析平台，并以美国农产品数据为例，讨论该方法的可行性。

关键词：多维数据；时空数据；SOM神经网络；可视化分析

中图分类号： S126 文献标志码： A 文章编号：1002-1302（2017）20-0244-05

伴随全球定位系统、遥感技术等技术的不断突破及在农业领域的广泛应用，产生了大量多维时空数据。这些数据有效记录并展示了事物各阶段的发展状况，是一种结构复杂、多层嵌套、具有空间和时态特征的高维数据[1]。由于数据在时间和空间上具有很强的相关性，蕴含巨大的挖掘潜力。如何挖掘和分析这些数据对于精细农业的发展、农业生产的进步及现代社会的发展有着极大的研究意义。

作为探索数据内在隐藏信息的一种手段，时空数据可视化方法通过对多维时空数据进行图形化表示，能够全面展示数据基本特征，实现数据之间的交互[2]。当前，多维时空数据的可视化方法除了传统的2D、3D显示技术，还可分为基于几何的技术、基于层次的技术、基于图标的技术、面向像素的技术和降维映射技术等[3-5]。除了降维映射技术，其他多维时空数据可视化方法多是将数据各个维度直接映射于某一实体，降维映射技术能够将多维或高维数据投影到二维或三维空间，以数据散点图显示数据集的聚类结构和数据分布，并显示聚类结果类标信息（不同的类可以用数字或颜色区分）[6]。因此被广泛应用于维度较高、数据量较大的信息可视化。

降维可视化方法关键在于降维或映射技术的选择[7]。当前降维可视化方法主要有主成分分析法、投影寻踪法、自组织映射法（SOM）和多维标度法等。雷君虎等通过主成分分析法实现对烟用香料图谱数据进行数据降维和香料分类[8]。闫绪娴运用投影寻踪聚类方法对中西部地区2000—2011年自然灾害社会易损性时空數据进行3个层面的空间特征和区域差异分析，从而对地区自然灾害社会易损性进行综合评价[9]。芮小平等利用自组织映射降维技术实现了对2003年中国“非典”的多维信息进行数据降维和可视化分析[10]。李权利用Sammon投影（一种典型的多维标度法）将多维数据映射到二维平面，从而实现对海量微博数据进行可视化分析[11]。

本研究采用SOM算法实现对高维数据的降维。原因在于SOM神经网络实现对数据降维的同时，能保留其拓扑结构不变，从而避免“维数灾难”的发生。同时，SOM将输入数据转换成数据量较小的矢量数据，数据在被其他投影技术分析和表达的同时，在较少计算量的情况下，能产生良好的投影结果。

考虑到多维数据多包含大量时空信息，单纯通过SOM降维可视化技术进行数据可视化，并不能很好地反映当前信息的时空特征。同时，针对某一问题的研究，由于采集数据的属性维度较多且存在差异性，即使采用多属性的时空数据可视化表达也无法保证其能够达到良好的可视化效果。有学者考虑使用多种可视化分析方法集成的模式对时空数据进行可视化分析表达，例如：Andrienko等利用SOM降维数据对美国41年间各州犯罪率时空数据进行降维分类，并在地图上进行各州犯罪情况的可视化展示，取得了良好的数据挖掘效果，提升了数据分析效率[12]。然而，这种多可视化方法集成的模式更多地还是集中于对原始数据的可视化表达，相互关联性并不强，且运算量较大，并不能很好地满足当前对时空数据全面、高效、动态的深入分析和挖掘要求。

针对单一的可视化方法无法满足时空数据多角度表示和分析的要求，集成的可视化方法更多也仅是对时空数据可视化工具的组合，本质上还是独立地对时空数据进行表达说明。本研究提出一种基于SOM的多视图协同可视化分析方法，该方法从对降维数据的可视化角度出发，集成多种可视化分析工具，针对降维后数据进行可视化表达，既解决了传统可视化分析工具无法对高维多属性时空数据进行可视化的问题，又做到各表达工具之间的联动，实现对数据的实时多角度可视化表达和分析，增强分析者对隐藏信息的挖掘能力。本研究以美国农业时空数据为例，搭建基于该方法的动态可视化分析平台，进行时空数据可视化分析，验证该方法的可行性，旨在为推进我国精细农业的发展提供依据。

1 基于SOM的降维可视化

1.1 基于SOM的聚类方法

1982年芬兰学者Kohonen根据人脑的生物学、生理学、心理学的研究成果，提出自组织映射网络（self-organizing feature map，SOM），别称kohonen网络，它是无监督学习的神经网络[13]。SOM网络主要面向高维数据，通过降维将数据从完全混乱转换为整体有序，从而挖掘感兴趣的特征。其学习过程是一个竞争过程，即调整一部分输入数据的权值使得权向量更接近或更偏离输入矢量，最终使得所有权向量都在输入空间内相分离，形成各自所代表的一类输入空间模式。具体算法过程如下：

设有m个输入样本，每个输入样本有n个属性，即输入为n维向量X=（x1，x2，…，xn），从而构成一个二维的神经元输入层。输出层由P个神经元节点构成，每个结点与一个权值相联系。其连接权值wi，j表示第i个输入神经元节点与第j个输出神经元节点之间的连接权值。

（1）初始化：为网络的权向量在[0，1]区间随机赋予1个值，要求互不相同，从而确定邻域的初始值。邻域是指以确定的获胜神经元为中心包含若干神经元的区域范围。

（2）接收输入并寻找获胜节点：对输入数据X进行归一化处理，计算权向量与X之间的欧氏距离，找出最小距离，确定获胜神经元i。endprint

式中：xi（t）表示t时刻输入样本数据值，i（x）即为最匹配神经元。

（3）定义优胜邻域：以获胜神经元为中心，确定权值调整值。

式中：ri（x）、rj分別为输入节点i（x）、j的位置，σ表示邻域范围，hj，i（x）（t）为值域函数，表示获胜神经元周围的邻域函数，随时间单调递减。

（4）调整权值：对邻域内所有神经元与输入层神经元之间的权向量进行修正。

式中：η（t）表示学习速率[0<η（t）<1]，随时间单调递减，保证学习过程收敛性。

（5）结束判定：更新学习速率及邻域，重复上述学习过程，直到对所有样本进行学习。

最后通过训练，连接权向量不再进行调整，所得网络拓扑能够近似描述输入向量分布情况，实现模式分类的目的。

1.2 基于SOM的降维可视化

基于SOM的高维数据可视化过程如图1所示，此前首先需要对输入的数据集进行预处理，规范其数据结构，保证数据为矩阵形式数据。对数据进行规范处理后，通过SOM神经网络算法进行数据降维。这个过程中，高维数据将通过降维映射到二维平面的神经元上，自组织映射网络中的神经元代表所需分析的高维数据，其所在位置能够反映数据的聚类信息，并保证其拓扑关系不变。然而SOM算法本身并不能将其所分析获得数据的聚类结构通过图形的方式展现，必须借助其他可视化方法进行显示。因此，SOM算法可视化过程的最后一步就是通过自组织映射网络可视化算法对自组织映射网络上的神经元进行数学运算，获得结果再由图形图像的形式进行可视化表达。当前，自组织映射网络的可视化方法使用最多的是U-Matrix算法可视化方法。

U-Matrix算法（unified distance matrix）又称为统一距离矩阵，由Ultsch等于1990年为了实现对Kohonen提出的SOM算法进行可视化表示而提出。该算法解决了SOM算法无法对聚类结果进行抓取的缺点，在SOM算法保证数据拓扑关系的情况下实现对聚类结构的提取和现实。基于U-Matrix算法的自组织映射网络可视化方法为一种基于距离度量的方法，其基本结构如图2所示，为一种二维网络形式的结构。SOM自组织映射网络中每个神经元分别对应U矩阵算法中4个网络节点，节点用于存储每一神经元与相邻神经元距离参数值。如节点1存储a与水平相邻神经元b的权向量之间距离，节点2存储a与纵向相邻神经元c的权向量之间距离，节点3存储a与对角线相邻神经元d的权向量之间距离，节点4存储这3个距离平均值。

考虑到数据进行SOM神经网络降维聚类后，不同的聚类数据之间相似性较小。通过距离度量表示就是距离越大其差异性越大，数据类型越不同，反之则为同一聚类。这就是 U-Matrix 可视化能够表达SOM神经网络聚类结果的主要依据。U-Matrix可视化通过对自组织映射网络中各神经元的权向量与其相邻神经元权向量之间进行距离运算获得运算结果，将之存储于U-Matrix网络中，并用不同颜色对数据值进行表示，从而实现对自组织映射网络中的聚类结构进行分离和显示[14]。通常，U矩阵二维网格多由六边形来表示，当U矩阵数值较大，则表示该位置为聚类的边缘部分，反之则为聚类本身。

2 基于SOM的协同多视图可视化

协同多视图可视化方法相较于传统的基于SOM的降维数据可视化方法，在利用U-Matrix算法可视化实现对其聚类结果拓扑关系显示的同时，引入平行坐标和时空立方体等可视化工具。前者通过折线为聚类后特征数据的属性关系进行直观二维平面可视化表达，补充说明数据各属性之间的关系。后者利用平面对聚类后特征数据的时空关系进行直观三维平面可视化展示，补充说明数据在时间和空间维度上特征关系。通过多种工具协同可视化，利用计算机组件实现数据的实时交互，对颜色等特征表示方法进行统一说明，从而增强各可视化工具之间的联系，达到时空数据多窗口协同效果，能够实现对高维数据的全方面可视化表达，增强可视化效果。

2.1 平行坐标可视化

作为高维数据在二维平面上较为经典的可视化表达方法，平行坐标（parallel coordinates）由Alfred在1985年提出，平行坐标是基于几何可视化技术的代表。其基本思想是将n维数据属性空间通过n条等距离的平行轴映射到二维平台上，每一属性维由一条轴线表示，轴线上的取值范围由对应属性的最小值到最大值均匀分布[8]。

平行坐标的优点在于能够通过射影几何解释和对偶特征直观地表达数据之间的关系，而不必使用矢量或其他可视图标，易于理解。缺点在于随着数据量的增大，折线密度增大导致大量交叠线，难于辨识[15]。研究对原始数据进行降维，再进行平行坐标可视化，能够很好地规避其缺点，并充分利用其优势对多维数据关系进一步补充说明。图3为基于SOM降维的平行坐标可视化结果，针对SOM降维所得聚类结果，获得每类中的数据典型作为输入变量，参考数据抽象、坐标轴交换、维数控制等基于平行坐标的可视化技术，按照数据属性维度设置平行轴，实现时空数据的可视化表达，并为各分类分配对应颜色，方便观察分析。

2.2 时空立方体可视化

时空立方体的概念最初于1970年由Hagerstraand提出，主要用于实现对时空路径的表达[16-17]。如图4所示，每个平面代表某地理现象在某时间段的变化情况，为一时间平面，由多个时间平面构成时空立方体，以此来表达时空数据的变化[18-19]。其主要优点在于能够将时空数据在三维的立方体中进行表达，突出表现地理现象随时间的变化情况。与平行坐标相似，当数据量较大且属性维度较多时，将造成平面交叠、路径混乱、多属性难以表示等问题。通过SOM降维技术对数据进行聚类降维后，数据属性维度减少，可以利用颜色表示其分类情况，借助地图等地理显示工具，完成时空数据表达，展示SOM降维后数据的时空属性关系，从而实现对高维时空数据的可视化。endprint

3 平台搭建及试验效果

3.1 平台搭建

为验证时空数据可视化分析方法的实际应用效果，以美国农产品时空数据为例，通过Visio studio 2010平臺，利用C#语言，建立基于SOM的美国农产品时空数据可视化分析平台。研究平台主要分为3个模块，分别为数据层、挖掘层、可视化界面层（图5）。

数据层用于存储时空数据，支持各模块进行数据调用。挖掘层基于SOM的高维数据降维和挖掘进行数据分类，为可视化提供数据基础。可视化界面层为平台可视化展示层，用于对数据进行可视化表达。可视化主要包括数据挖掘前后的可视化表示方式2种，前者主要用于对数据进行检索，通过数据检索获取感兴趣的数据源，后者主要是对前者选取的数据源进行基于SOM降维聚类后的数据可视化表达。主要表达工具有U-Marrix算法、平行坐标、时空立方体等。

3.2 研究数据源

研究数据源为美国NASS网站的农业调查数据，其原始数据按照年份与地域尺度（州、县）进行划分，主要分为农作物、动物及产品、农业经济、农业环境4部分数据，其中农业经济数据包括农业资产和农业租借费用两方面。鉴于原始数据的缺陷，首先对数据进行筛选处理，最终用于本研究的数据源为其农作物数据源。数据主要包含美国50个州2001—2010年19种农产品各自的总面积、总收成及总产量。

3.3 试验效果

对数据进行归一化处理后，输入SOM神经网络进行数据降维，并对结果进行可视化展示。将可视化流程和平台设计最终所得可视化结果通过农业时空数据可视化平台的可视化界面层进行展示，达到数据的多角度显示和分析的作用，结果如图6所示。

3.3.1 时空数据视图窗口 时空数据视图窗口由时空数据选择窗口和时空数据表视图窗口两部分组成。通过时空数据选择窗口对最初的多维时空数据进行选择，并将筛选出的数据以二维表的形式在时空数据表视图窗口显示。其目的在于实现用户与系统之间交互，通过对海量数据的筛选，达到任意时空、属性维度数据挖掘和分析的目的。本研究按照年份和属性选择2001、2003、2005、2007、2009年的大麦、大豆、马铃薯、小麦、燕麦的总面积等5个属性数据，探索其间关系。

3.3.2 SOM神经网络视图窗口 SOM神经网络视图窗口显示数据进行SOM神经网络聚类降维后，进行U-Marrix算法可视化的结果。窗口左图为U矩阵图，右图为labels图，按照U矩阵图，灰度深浅表示相邻区域距离的远近，颜色大小是权重的多少，labels图上显示最为代表性的区域及其时间。2005年亚拉巴马州的数据（1—2005）和2005年俄克拉何马州的数据（40—2005）分别最为接近此时权重的代表值。研究基于SOM的神经网络可视化主要通过Matlab软件实现，采用混合编程的模式，利用SOM Toolbox作为SOM神经网络的软件工具，利用Matlab软件中Deploytool工具将m函数编译为 .NET 程序集，再由C#软件调用。

3.3.3 平行坐标视图窗口 平行坐标视图窗口用于对SOM神经网络视图窗口中显示的代表性区域的某年数据信息的补充说明。如在SOM神经网络视图显示的权重最小的2005年俄克拉何马州数据，其大麦、大豆、马铃薯、小麦、燕麦的总面积的参数分别为0、325 000、0、5 700 000、45 000。同时，通过轴线形象化表示，达到最直观的比较数据参数的目的。如在代表性数据中，大豆、马铃薯总面积最大的是2005年爱达荷州（16—2005），燕麦总面积最大的是加利福尼亚州（6—2005）。平台平行坐标可视化功能直接在VS上由C#中 GUI+界面设计完成。

3.3.4 时空立方体视图窗口 时空立方体窗口的每一平面代表某一年份以显示地理空间属性数据，其区域颜色与SOM神经网络算法颜色匹配。研究主要通过在VS平台上应用ArcEngine组件库，将ArcScene的3D建模移植到平台窗口，进行时空立方体的构建。通过观察颜色的变化情况，可直观看出随年份的变化各地区颜色变化情况。如俄勒冈州，颜色从2001、2003、2005、2007年的橙色到2009年的绿色；华盛顿州、蒙他拿州、爱达荷州、北达科州等没有发生颜色的变化。

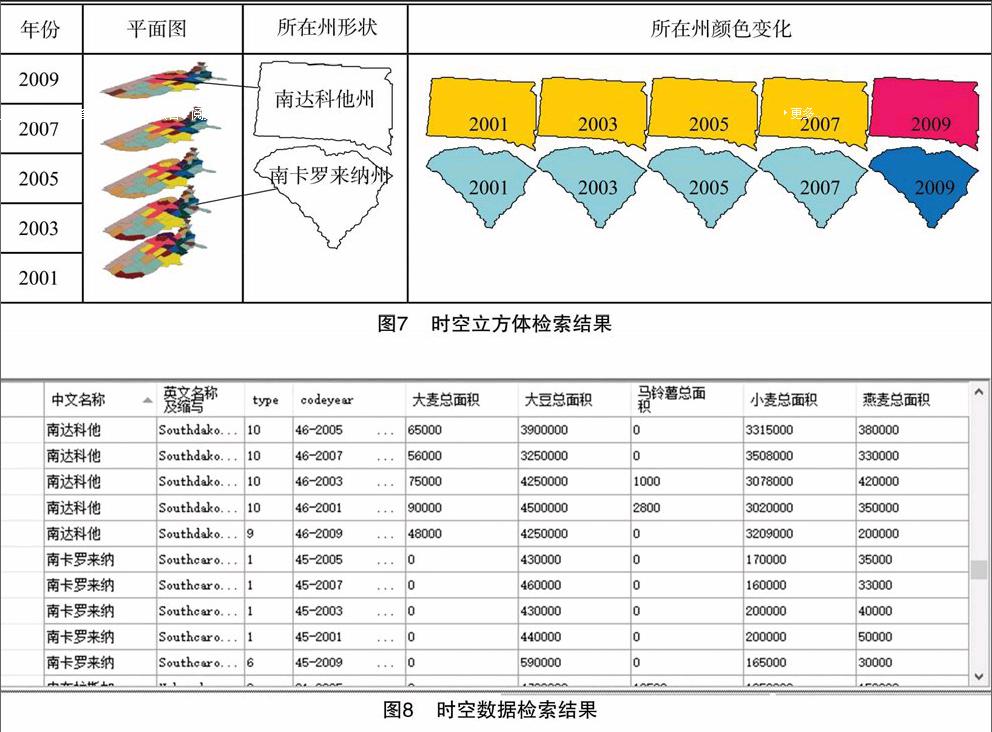
3.3.5 平台协同多视图实现 通过在时空数据视图窗口对研究数据进行筛选，获取所需研究数据进行SOM降维，在对降维数据进行可视化表达后，获得各个窗口的显示结果，通过对结果进行观察可获得数据内在联系，挖掘有用信息。例如，对时空立方体视图窗口进行观察，由图7可知，南达科他州的颜色变化从2001、2003、2005、2007年的深粉色变成2009年的黄色，同样的还有南卡罗来纳州，其颜色变化从2001、2003、2005、2007年的浅蓝色变成2009年的灰蓝色，说明2个州在前4年作物种植面积相似，而2009年有一定变化。针对这一现象，对时空数据视窗口显示的相关数据进行观察（图8），发现南达科他州的作物种植面积的确在2009年较前几年有明显改变，表现在大麦、燕麦总面积有明显减少。南卡罗来纳州也存在相似情况，2009年大豆总面积有明显提升。同样的，对SOM神经网络视图窗口所得结果观察可知，浅蓝色在时空数据显示上最具代表性，数据向2005年亚拉巴马（1—2005）数据聚拢。这一结论亦可由时空立方体视图窗口显示结果观察获得：从时空立方体平面图展示结果来看，2001、2003、2005、2007、2009年作物生产面积上大部分显示浅蓝色。当需要研究这一聚类数据维度关系具体情况时，可通过平行坐标窗口观察获得。

总体而言，利用SOM降维技术对高维数据进行聚类降维后，通过U-Marrix算法、平行坐标和时空立方体等可视化工具对时空数据进行协同可视化表达，能够解决传统的SOM降维可视化表达对高维时空数据时空关系说明存在的缺陷，清晰展现多维农业时空数据在时间维度上的地理空间变化，说明数据的聚集和分布情况，方便对数据的潜在关系进行挖掘和分析。endprint

4 结论

通过聚类降维算法和多种其他可视化方法的结合使用，实现多视窗协同可视化，克服了单一的可视化方法存在的维度、样本量限制等问题，较大地提高挖掘效率，为多维时空数据的分析挖掘提供新思路，在对海量农业数据挖掘和分析中，能够提供良好的技术支持，有利于精细农业的发展和推广，具有一定的经济效益和社会效益。然而，不同聚类方法对数据集的拓扑特性拟合能力不同，导致聚类准确性存在差异，同时不同可视化方法数据可视化表达侧重点各有不同。对此，针对不同农业数据集，如何寻找合适的聚类降维算法，如何确定其拓扑分布，判断其聚类准确性，选用合适可视化工具展示其时空关系，值得进一步研究。

参考文献：

[1]钟运琴，方金云，赵晓芳. 大规模时空数据分布式存储方法研究[J]. 高技术通讯，2013，23（12）：1219-1229.

[2]齐 志. 基于SOM神经网络的聚类可视化方法研究[D]. 长春：东北师范大学，2009.

[3]李 杨，郝志峰，谢光强，等. 质量度量指标驱动的数据聚合與多维数据可视化[J]. 智能系统学报，2013，8（4）：299-304.

[4]杨彦波，刘 滨，祁明月. 信息可视化研究综述[J]. 河北科技大学学报，2014，35（1）：91-102.

[5]Thakur S，Hanson A J. A 3D visualization of multiple time series on maps[C]. Proceedings of the Proceedings of the International Conference Information Visualisation，2010：336-343.

[6]刘 芳，Tian K，Zhou Z G，et al .基于SOM聚类的可视化方法及应用研究[J]. 计算机应用研究，2012，29（4）：1300-1303，1306.

[7]王开军. 多维数据的聚类结果可视化技术综述[J]. 福建师范大学学报（自然科学版），2012，28（4）：115-124.

[8]雷君虎，杨家红，钟坚成，等. 基于PCA和平行坐标的高维数据可视化[J]. 计算机工程，2011，37（1）：48-50.

[9]闫绪娴. 中西部地区自然灾害社会易损性空间特征分析[J]. 经济地理，2014，34（5）：34-40.

[10]芮小平，张立强. 基于SOM的多维信息可视化研究[J]. 应用基础与工程科学学报，2011，19（3）：379-388.

[11]李 权. 面向多维数据及微博社交网络的可视分析技术的研究[D]. 北京：清华大学，2012.

[12]Andrienko G，Andrienko N，Bremm S，et al. Space-in-time and time-in-space self-organizing maps for exploring spatiotemporal pattens[J]. Computer Graphics Forum，2010，29（3）：913-922.

[13]Obu-Cann K，Fujimura K，Tokutaka H. Data ming of power transformer database using self-organising maps[J]. Proceedings of ICU International Conferences on Info-tech and Info-net，2001，18（4）：44-49.

[14]Vesanto，Alhoniemi E. Clustering of the self-organizing map[J]. IEEE Transactions on Neural Networks，2000，11（3）：586-600.

[15]孙 扬，唐九阳，汤大权，等. 改进的多变元数据可视化方法[J]. 软件学报，2010，21（6）：1462-1472.

[16]Qi F，D Fei. Tracking and visualization of space-time activities for a micro-scale flu transmission study[J]. International Journal of Health Geographics，2013，12（1）：6.

[17]Gatalsky P，Andrienko N，Andrienko G. Interactive analysis of event data using space-time cube[C]. Proceedings Eighth International Conference on IEEE，2004：145-152.

[18]Hadlak S，Tominski C，Schulz H J，et al. Visualization of attributed hierarchical structures in a spatiotemporal context[J]. International Journal of Geographical Information Science，2010，24（10）：1497-1513.

[19]吴正升，胡 艳，何志新. 时空数据模型研究进展及其发展方向[J]. 测绘与空间地理信息，2009，32（6）：15-17，21，24.endprint