城市马拉松赛参赛者位次变化分布及其与竞争程度的关联的研究

孟 帆

(温州大学物理与电子信息工程学院，浙江温州 325035)

城市马拉松赛参赛者位次变化分布及其与竞争程度的关联的研究

孟 帆

(温州大学物理与电子信息工程学院，浙江温州 325035)

近十多年来，人类动力学领域关于时间特性和空间特性的研究迅猛发展.本文统计近十多年来纽约城市马拉松赛和近四年来波士顿马拉松赛前1000名男子参赛者和前1000名女子参赛者的参赛数据，分析参赛者在7个中间计时赛段中的位次变化情况，发现参赛者在各中间计时赛段中的位次变化均遵循洛伦兹分布（柯西分布）.引入参赛者在各计时赛段内的位次变化的方均根值来描述该赛段内的竞争激烈程度，进一步研究各计时赛段内竞争激烈程度与位次变化分布参数的关联，发现在各中间计时赛段中参赛者的位次变化分布图形的尖锐程度能直观地反映该赛段内参赛者的竞争激烈程度，参赛者在某赛段内的竞争激烈程度越低，该赛段内参赛者的位次变化分布曲线越尖锐.

人类动力学；城市马拉松赛；中间计时赛段；位次变化分布

2005年Barabási发现了人类通讯行为的非泊松分布特性，开启了挖掘人类行为大数据并从中揭示人类行为规律的研究热潮[1]，其中关于人类行为时间特性和空间特性的实证统计和模型的研究居多.在人类行为时间特性方面，物理学家和其它领域学者在大量实证统计和分析的基础上发现人类行为时间特性普遍存在幂律分布现象，包括通信[1-3]、各种网上社交活动[4-6]等等.针对这些非泊松分布的时间行为，有关学者提出了许多种人类行为模型以解释这些非泊松过程的微观机制，主要有优先级排队模型[1-7]、社会交往模型[8-9]以及个人兴趣模型[10]等等.

随着对人类行为时间特性的研究深入，研究者又将人类动力学研究推向了另一个方面——人类行为的空间特性.Brockmann等人[11]通过对美国钞票流通数据的研究间接地得出了人类的移动轨迹，发现在1到4天时间间隔里人类移动距离的概率服从幂律分布，他们认为人类移动轨迹类似于动物移动轨迹，可以用Lévy模型来描述人类的空间移动，认为人类运动轨迹非常符合连续时间随机游走模型.随后González等人[12]用100000名匿名用户的手机统计了6个月的移动数据得出个体运动位移的分布近似满足一个截断幂律分布的结论，他们的研究结果表明，人类轨迹相对于Lévy飞行模型暗示的随机轨迹有高度的空间规律性，即每个个体都有与时间无关的移动距离特征，并且返回几个经常光顾的地点的概率很高.随后，Song等人[13]表示针对手机用户得到的数据得出整个的手机用户群体的空间运动模式有 93%的可预测性，且不同个体运动模式的可预测性基本没有差别.之后，又建立了探索偏好返回机制来解释人们在到达一个新的地点之后还会在未来某一时刻返回该地点的行为，即每个个体会产生一个周期性的和相对稳定的流动模式[14-16].此外，还有很多基于其它原因而建立的模型，例如社会交互模型[17]，交通网络分布模型[18]等.然而，之后一项研究表明，当集体位移分布符合截尾幂律分布时绝大多数的个体行为距离是偏离幂律分布的[19]，说明不能由群体运动模式直接推出个体的运动模式.也有研究者根据出租车的数据得出短途行驶距离（小于 30英里）遵循幂律分布，而长途行程遵循指数衰减规律，并发现个体出租车的行驶距离规律并不是之前研究得出的截尾幂律[20].随后研究者们将对人类运动行为的空间特性的探究拓展到了实际生活中.Wang等人对城市人口的流动方式及其空间分布对人口流动的影响进行了研究，发现在城市地区较大尺度空间中人类行程长度遵循的并不是幂律分布而是指数分布，并发现规模较大的城市区域一般有较小的指数行程长度分布，且行程长度有较大的平均数和标准差，空间人口密度和行程长度并没有明显的联系[21].

在人类运动行为中，速度是一个不可忽略的重要特征，而在人类行为研究的多元化发展中，对于速度的研究却寥寥无几.有研究发现，在没有驾驶员的起源地、目的地、驾驶习惯、导航策略和适应性行为的先验知识情况下，只依赖于短期的历史GPS车辆记录，便可高度预测车在北京的三个主要环形公路的平均速度，从而可捕捉到城市道路上的交通模式[22].无论是采用混合还是单一的交通方式，速率随着运动距离的增加都是呈现增加的趋势，并遵循幂律分布[23].

马拉松赛是一个竞争性项目，在比赛中较量的就是参赛者的速率，而跑过或看过马拉松赛的人都知道，在比赛中保持稳定的配速是明智之举.起跑过快的人通常对自己的体力有一个错误的估计，认为自己的起跑速度可以一直保持下去，但是随着比赛的进行速度往往会慢下来，甚至还会步行或麻木地拖着双腿挪动，导致最终取得一个很差的位次.因为生理和心理上的差异，使得每个人的配速策略不同，这也是导致参赛者的位次发生改变的主要原因.本文将探究马拉松赛中间计时赛段参赛者位次变化的分布规律，探究位次分布变化与竞争激烈程度之间的关系，间接地研究城市马拉松赛赛程中参赛者的群体行为特征，从而进一步探究在群体层面上个体之间的相互作用的影响.

1 数 据

纽约城市马拉松赛记录数据中除了有各完成赛程者完成全程的时间之外，还记录了参赛者到达赛程中间5km、10km、15km、20km、25km、30km、35km、40km处的时间，我们从纽约城市马拉松赛记录数据中收集了自2001年到2016年总计15年（2012年纽约马拉松赛因为飓风“桑迪”而取消）共计615990条的完成赛程者的比赛记录（平均每年完成赛程的人数为41066）.波士顿马拉松赛记录数据中除了有所有完成赛程者完成全程的时间，仅记录了男子组和女子组前1000名参赛者到达赛程中间5km、10km、15km、20km、25km、30km、35km、 40km处的时间，我们从波士顿马拉松赛记录数据中收集了自2013年到2016年共计4年8000条完成赛程者的比赛记录.这些数据为我们研究参赛者在中间赛段内的速度和位次变化的分布规律提供了依据.考虑参赛者性别因素对速度和位次变化的影响，我们将全部完成赛程者分为男子组和女子组.根据纽约城市马拉松赛和波士顿马拉松赛中间计时位置，我们将马拉松赛全程分成8个5km长的赛段，这里用i=1, 2,…, 8表示0–5km、5–10km、10–15km、15–20km、20–25km、25–30km、30–35km、35–40km等赛段，通过实证统计分析，研究参赛者在各中间赛段的位次变化规律.

2 中间计时赛段参赛者位次变化分布

根据每位参赛者到达赛程中间计时点的时间，我们得到各参赛者在各赛段结束时的位次和在该赛段的位次变化，如根据第k位参赛者是该场城市马拉松赛的总人数)到达第i个计时点（即第i个赛段结束时）的时间tik，可得到该参赛者在第i赛段结束时的位次rik，以及在第i赛段中的位次变化由于第一赛段的起始点是整个赛程的起点，所有参赛者还没有形成位次分布，故本文不分析参赛者在第一赛段的位次变化.

对每一赛段计算得到各参赛者的位次变化Δrik.考虑N位参赛者位次变化Δrik的数据波动往往会很大，我们建立一系列长度为10的区间，用n表示（n为整数），即第n区间的位次变化Δrik的范围为由此来对参赛者位次变化Δrik进行装箱（Binning），由于波士顿马拉松赛仅记录了前1000名参赛者到达赛程中间时段处的时间，因此对于波士顿马拉松赛的数据装箱的区间长度为5，即第n区间的位次变化Δrik的范围为计算位次变化在第n区间内的参赛者的人数及其位次变化Δrik的平均值由此得出位次变化Δrik的各区间内的参赛者的人数占总人数的比例与位次变化落在该区间内的参赛者的位次变化的平均值的数据，进一步画出第i赛段参赛者人数比例随参赛者位次变化的分布图（如图1）.2016年纽约马拉松赛和波士顿马拉松赛各中间计时赛段男子组和女子组的随变化的情况见图1.最后通过数据曲线拟合得出随变化的分布函数，这里采用调整后值（Adjusted R-square）的大小来反映拟合的优度，确定拟合的模型函数.结果发现，在纽约马拉松赛和波士顿马拉松赛中各中间计时赛段内男子组和女子组的位次变化分布基本保持一致，均遵循洛伦兹分布：

洛伦兹分布又名柯西分布，拥有比高斯分布更宽的尾部，是一个稳定的“胖尾”分布，具有无穷大的方差[24-26]，这种方差条件说明：非常高或者非常低的位次变化发生的频率会比在正态分布中发生得更高，如在2016年纽约马拉松赛中男子参赛者总人数为29549人，男子参赛者在5 –10km赛段中位次变化的绝对值大于2955（即在比赛中超过2955人或落后2955人）的人数占总人数的3%，而其它赛段的位次变化的绝对值大于2955的男子参赛者的人数约占总人数的1%，这部分参赛者的存在导致了位次变化分布的尾部比高斯分布的尾部宽.

洛伦兹分布，常出现在金融系统中，金融系统是一个人为作用非常大的复杂的经济社会系统，43个国家57个行业中的13342家公司1999–2010年的利润率分布满足柯西分布[24]，全世界167个国家1950–2011年的GDP增长率也遵循柯西分布[25].在金融系统中，经济体的异质性和彼此之间的学习、竞争导致了生产力和盈利能力的增长率呈现“胖尾”分布的特性[27].与此类似，我们认为城市马拉松赛中参赛人数众多，参赛者之间的巨大能力差异和赛跑过程中的强竞争性是导致参赛者位次变化呈现“胖尾”分布的主要原因.

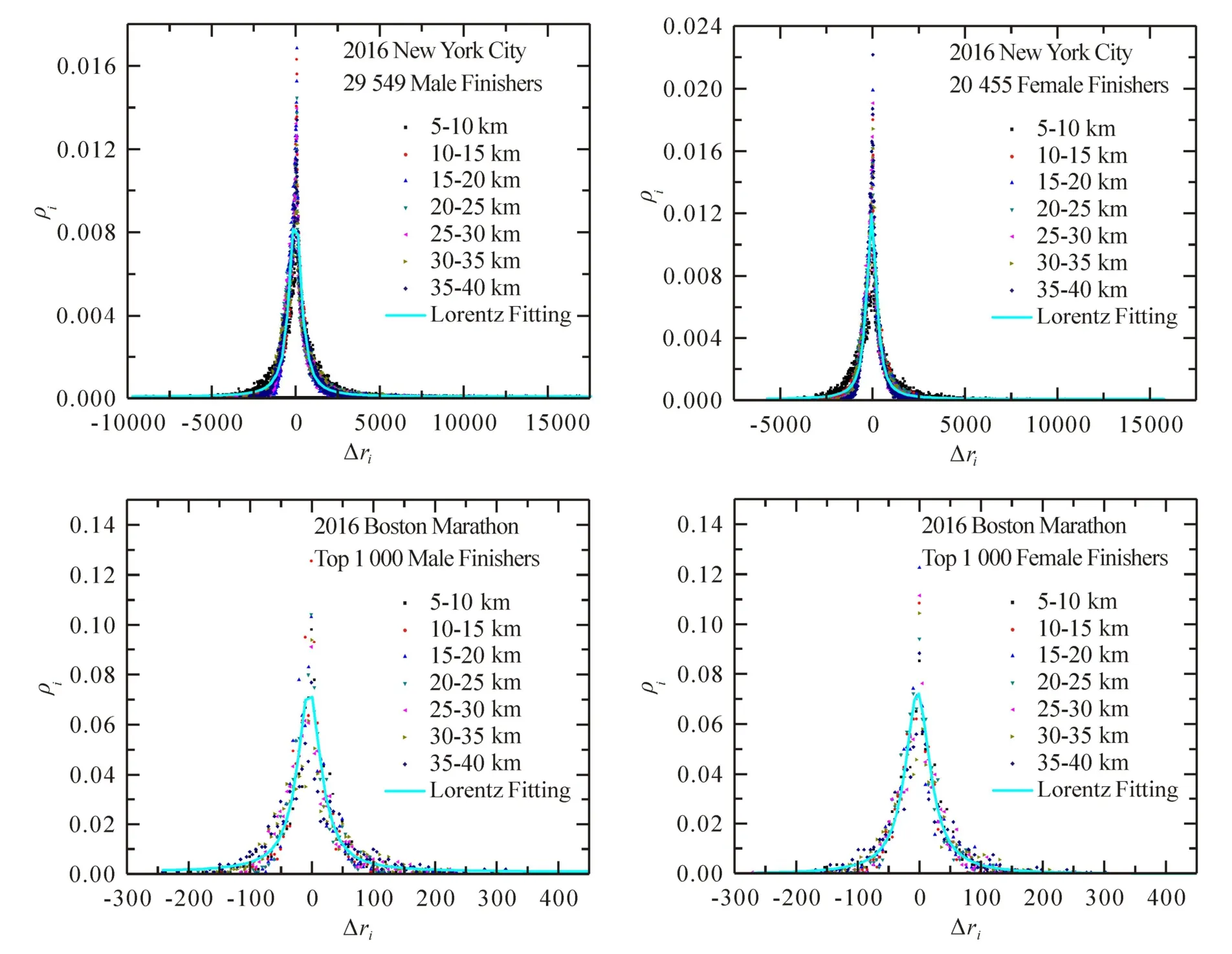
图1 2016年纽约马拉松赛和波士顿马拉松赛男子组和女子组在7个中间计时赛段的位次变化分布Fig 1 Distributions of Ranking Changes of Male and Female Finishers in Seven Intermediate Time-trials in 2016 New York City Marathon and Boston Marathon

3 位次变化分布与竞争激烈程度的关联

从图1所示的参赛者在中间计时赛段的位次变化分布可以看出，参赛者在各段中的位次变化趋势基本保持一致，但还是能观察到一些不同的地方，因此在本小节将考虑各计时赛段位次变化分布之间的差异与影响因素.从图1中可以观察到不同年份的纽约马拉松赛和波士顿马拉松赛中男子组和女子组的位次变化分布基本保持一致，本节选取 2016年纽约马拉松赛男子组为例进行数据处理与分析.

如图2所示，将2016年纽约马拉松赛男子组在各计时赛段位次变化的分布两两分开放到图中比较，以避免由于数据点的堆积导致分布之间的差异被掩盖.

从图2可以明显看出，2016年纽约马拉松赛男子组在各中间计时赛段的位次变化分布高度与宽度的不同，在波士顿马拉松赛中前1000名男子参赛者和前1000名女子参赛者的中间计时赛段的位次变化有同样的现象.对男子组在7个中间计时赛段的位次变化分布分别拟合的曲线进行分析与研究，在男子组各计时赛段位次变化分布遵循的柯西分布拟合过程中，除了可以得到峰值位置x0和半峰半宽度ω外，还可以得到拟合分布的高度发现半峰半宽度ω值和高度 H值在不同计时赛段中的大小差异很大.我们设想在不同计时赛段的半峰半宽度ω值和高度 H值与该赛段内参赛者竞争的激烈程度有关，尝试用各计时赛段内全部参赛者的位次变化的方均根值（σ）描述该赛段内参赛者的竞争激烈程度：

其中N为参赛者总数.

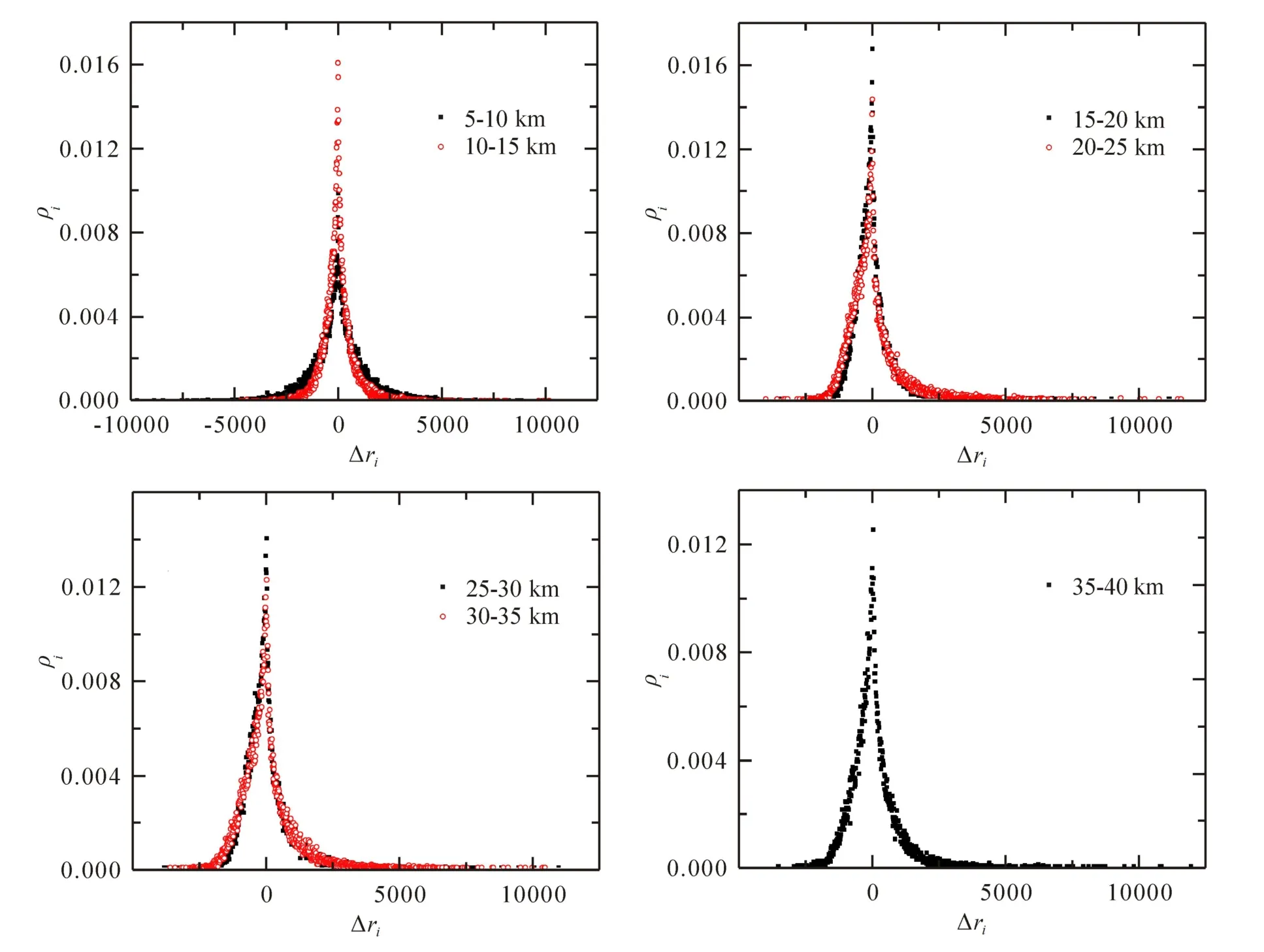
图2 2016年纽约马拉松赛男子组在7个中间计时赛段的位次变化分布Fig 2 Distributions of Ranking Changes of Seven Men’s Intermediate Time-trials in 2016 New York City Marathon

将2015年和2016年纽约马拉松赛和波士顿马拉松赛男子组和女子组在各计时赛段的位次变化的方均根值σ与位次变化分布的ω和H值列于表 1，不同计时赛段半峰半宽度ω值和分布高度H值随位次变化方均根值σ的变化见图3和图4.

从图3可以发现半峰半宽度ω值与位次变化方均根值σ成明显的线性正相关，年和 2016年纽约马拉松赛男子组的α值相差不大，α≈1；女子组的α值相差也不大，α≈0.89.2015年和2016年波士顿马拉松赛男子组的α值相差不大，α≈0.9；女子组的α值相差较大，但还是成明显的线性正相关.

从图4可以发现高度H值与位次变化方均根值σ成明显的线性负相关，2015年和 2016年纽约马拉松赛男子组的β相差不大，女子组的β相差也不大，

2015年和2016年波士顿马拉松赛男子组和女子组的β略微不同，但可以观察到明显的线性负相关.

由此，可以进一步得出一个结论，即马拉松比赛各中间计时赛段中参赛者的位次变化分布图形的尖锐程度可以直观地反映该赛段内参赛者的竞争激烈程度，某赛段内竞争激烈程度越低，则该赛段内参赛者的位次变化分布曲线越尖锐.

表1 2015年2016年纽约马拉松赛和波士顿马拉松赛中间计时赛段位次变化的方均根值（σ）和位次变化分布ω和H值Table 1 The Ranking Change Distribution of ω and H and Root-mean Square Value of Ranking Change in Intermediate Time-trial in 2015 and 2016 of New York City Marathons and Boston Marathons

图3 纽约马拉松赛和波士顿马拉松赛中间计时赛段半峰半宽度ω值与位次变化方均根值σ的关联情况Fig 3 The Correlation between the Value ω of FWHM and the Root Mean-square Value σ of Ranking Changes for the Intermediate Time-trial in New York City Marathons and Boston Marathons

4 结论和讨论

本文统计了近十来年纽约马拉松赛和近四年来波士顿马拉松赛前1000名男子参赛者和前1000名女子参赛者的参赛数据，分析研究了城市马拉松赛过程中的人类运动行为.根据不同的计时点将纽约马拉松赛和波士顿马拉松赛全程分为8个计时赛段，分别是0–5km、5–10km、10–15km、15–20km、20–25km、25–30km、30–35km、35–40km.主要研究分析了纽约马拉松赛和波士顿马拉松赛中间计时赛段内参赛者位次变化的分布，由于第一赛段的起始点是整个赛程的起点，所有参赛者还没有形成位次分布，故本文主要研究后面7个计时赛段内参赛者的位次变化.结果发现参赛者在各中间计时赛段的位次变化分布均遵循洛伦兹分布（柯西分布），说明了在马拉松赛中间计时赛段中总有一部分参赛者有强大的竞争力会产生较大的位次变化，使位次变化分布呈现“胖尾”分布.对参赛者在中间计时赛段的位次变化分布进一步研究分析发现，竞争越激烈的赛段中，参赛者位次变化分布的半峰半宽度ω值越大，而高度H越小，即位次变化分布的图形越平缓；而竞争较小的赛段中，位次变化分布的半峰半宽度ω值较小，高度H较大，位次变化的图形比较尖锐，这说明在马拉松比赛中参赛者在各中间计时赛段的位次变化分布在一定程度上能直观反应竞争的激烈程度.

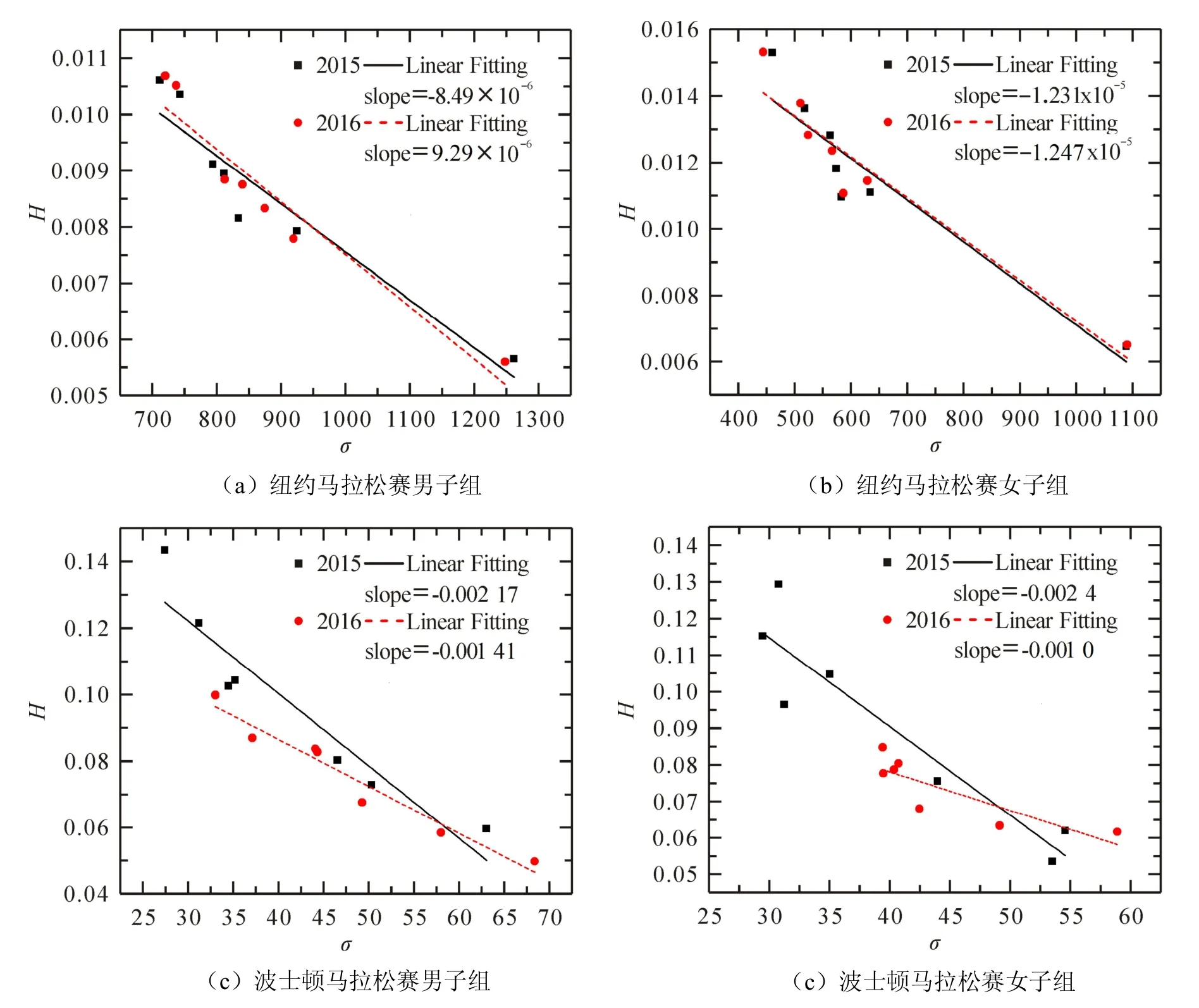
图4 纽约马拉松赛和波士顿马拉松赛中间计时赛段分布高度H值与位次变化方均根值σ的关联情况Fig 4 The Correlation between Distribution Height of the H and the σ of Ranking Changes of Intermediate Time-trial in New York City Marathon and Boston Marathons

对近十几年来的纽约马拉松赛和近几年的波士顿马拉松赛的分析得出同样的结果，说明了在马拉松赛这种群体运动过程中有着基本相同的机制存在，也说明了在群体运动中个体之间的相互作用确实存在，这对人类群体运动行为的研究具有重要意义.

[1] Albert-László B. The origin of bursts and heavy tails in human dynamics [J]. Nature, 2005, 435(7039): 207-211.

[2] Oliveira J G, Albert-László B. Human dynamics: darwin and Einstein correspondence patterns [J]. Nature, 2005,437(7063): 1251.

[3] Li N N, Zhang N, Zhou T. Empirical analysis on temporal statistics of human correspondence patterns [J]. Physica A,2008, 387(25): 6391-6394.

[4] Hu H B, Han D Y. Empirical analysis of individual popularity and activity on an online music service system [J].Physica A, 2008, 387(23): 5916-5921.

[5] Zhao Z D, Zhou T. Empirical analysis of online human dynamics [J]. Physica A, 2012, 391(11): 1019-1025.

[6] Dezsö Z, Almaas E, Lukács A, et al. Dynamics of information access on the web [J]. Phys Rev E, 2006, 73(6):066132.

[7] Vázquez A, Oliveira J G, Dezsö Z, et al. Modeling bursts and heavy tails in human dynamics [J]. Phys Rev E, 2006,73(3): 036127.

[8] Oliveira J G, Vazquez A. Impact of interactions on human dynamics [J]. Physica A, 2009, 388: 187-192.

[9] Zhou B, Qin S, Han X P, et al. A model of two-way selection system for human behavior [J]. Plos One, 2014, 9(1):e81424.

[10] Han X P, Zhou T, Wang B H. Modeling human dynamics with adaptive interest [J]. New J Phys, 2008, 10(7):1983-198.

[11] Brockmann D, Hufnagel L, Geisel T. The scaling laws of human travel [J]. Nature, 2006, 439(7075): 462-465.

[12] González M C, Hidalgo C A, Albert-László B. Understanding individual human mobility patterns [J]. Nature, 2008,453(7196): 779-782.

[14]Song C M, Qu Z H, Nicholas B, et al. Limits of predictability in human mobility [J]. Science, 2010, 327(5968):1018-1021.

[15] Song C M, Tal K, Wang P, et al. Modeling the scaling properties of human mobility [J]. Nat Phys, 2010, 6(10):818-823.

[16] Brockmann D, Brockmann D. Statistical mechanics: the physics of where to go [J]. Nat Phys, 2010, 6(10): 720-721.[17] Cho E, Myers S A, Leskovec J. Friendship and mobility: user movement in location-based social networks [EB/OL].[2017-01-08]. http://www-cs.stanford.edu/people/jure/pubs/mobile-kdd11.pdf.

[18] Jiang B, Yin J J, Zhao S J. Characterizing the human mobility pattern in a large street network [J]. Phys Rev E, 2009,80(2): 021136.

[19] Yan X Y, Han X P, Wang B H, et al. Diversity of individual mobility patterns and emergence of aggregated scaling laws [J]. Sci Rep, 2013, 3(9): 2678.

[20] Cai H, Zhan X W, Zhu J, et al. Understanding taxi travel patterns [J]. Physica A, 2016, 457: 590-597.

[21] Wang J, Mao Y, Li J, et al. Predictability of road traffic and congestion in urban areas [J]. Plos One, 2015, 10(4):e0121825.

[22] Chen W, Gao Q, Xiong H G. Uncovering urban mobility patterns and impact of spatial distribution of places on movements [J]. Int J Mod Phys C, 2016, 28(1): 1750004.

[23] Varga L, Kovács A, Tóth G, et al. Further We Travel the Faster We Go [J]. Plos One, 2016, 11(2): e0148913.

[24] Williams M A, Baek G, Park L Y, et al. Global evidence on the distribution of economic profit rates [J]. Physica A,2016, 458: 356-363.

[25] Williams M A, Baek G, Li Yiyang, et al. Global evidence on the distribution of GDP growth rates [J]. Physica A,2017, 468: 750-758.

[26] Williams M, Pinto B, Park D. Global evidence on the distribution of firm growth rates [J]. Physica A, 2015, 432:102-107.

[27] Dosi G, Lechevalier S, Secchi A. Introduction: interfirm heterogeneity: nature, sources and consequences for industrial dynamics [J]. Ind Corp Change, 2010, 19(6): 1867-1890.

(编辑：王一芳)

The Study on the Correlation between Participant Ranking Variation Distribution and the Level of Competition in City Marathons

MENG Fan
(College of Physics and Electronic Information Engineering, Wenzhou University,Wenzhou, China 325035)

In recent 10 more years, the research of the time response and spatial characteristics in human dynamics area has been rapidly developed. The datasets from the records of the participants of top1000 male athletes and top 1000 female athletes in both New York City marathons for recent 10 years and Boston marathons for recent 4 years are counted in this paper. From the above datasets, the runners’ ranking changes in 7 different internal timing lengths are also analyzed and therefore the ranking changes are always abide by Lorentz Distribution (Cauchy Distribution) during their participation in the mediate time trials. The competition fierce degree is described through the introduction of root-mean-square value of ranking changes in all time trial stages. The fierce degree of distribution graph for ranking changes in mediate time trials is discovered via further research on the correlation between the competition fierce degree and the variation distribution parameters, which reflects intuitively the competition fierce degree in such a contest. In conclusion, the lower the participant has competition fierce degree, the sharper the ranking change distribution curve of the participant becomes in such a time trial length.

Human Dynamics; City Marathons; Intermediate Time Trial Lengths; Distributions of Ranking Changes

N94

A

1674-3563(2017)04-0036-10

10.3875/j.issn.1674-3563.2017.04.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2017-04-06

国家自然科学基金(10875086)

孟帆(1993- )，女，江苏盐城人，硕士研究生，研究方向：复杂系统与统计物理