近断层脉冲型地震动作用下大跨斜拉桥地震响应分析

2017-11-30颜晓伟王景全

振动与冲击 2017年21期

张凡，李帅，颜晓伟，王景全

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室，南京 210096； 2.东南大学国家预应力工程技术研究中心，南京 210096；3.上海市市政规划设计研究院，上海 200040)

张凡1,2，李帅1,2，颜晓伟3，王景全1,2

为研究近断层脉冲效应和土-结构相互作用(SSI效应)对大跨斜拉桥地震响应的影响规律，以苏通大桥斜拉桥为研究对象，采用系统化的集总参数模型表征地基土的动力特性，建立了考虑SSI效应的结构动力数值计算模型，计算分析了破裂前方效应脉冲、滑冲效应脉冲和无脉冲三组近断层地震动作用下结构的地震响应。计算结果表明：相对于塔底固结模型，SSI效应降低了斜拉桥自振频率，并改变了高阶振型的产生次序；近断层地震动作用下，SSI效应可增大主塔位移响应，对其内力有削弱作用，并可降低纵桥向激励时主梁的位移和内力响应，但横桥向激励时，脉冲效应地震动作用下SSI效应明显增大了主梁的响应；脉冲效应地震动引起斜拉桥地震响应明显高于无脉冲地震动，滑冲效应主要影响纵桥向激励时主塔响应以及纵桥向(或横桥向)激励下主梁响应，破裂前方效应对横桥向激励下主塔响应影响更加显著。研究成果可为大跨斜拉桥在近断层地震动作用下的抗震设计提供借鉴。

近断层地震动；破裂前方效应；滑冲效应；系统化集总参数模型；土-结构相互作用；大跨斜拉桥

近年来，斜拉桥在大型跨海、跨江工程中优势显著，对于该类桥梁，随桥跨增加，结构刚度大幅下降，自振周期显著延长，超千米级斜拉桥的基本周期甚至超过10 s，在长周期地震动作用下其地震响应尤为显著[1]。国内外学者针对斜拉桥地震响应开展了大量研究，并取得了一些有益成果[2-6]，然而目前尚缺乏针对近断层地震动作用下斜拉桥抗震性能的研究。

破裂前方效应和滑冲效应是近断层地震动显著区别于远场地震动的重要特性，其呈现出长周期、高幅值等显著特点，如集集地震中TCU053站台测得的地震动脉冲周期甚至超过了13 s，脉冲型地震动对长周期结构的不利响应亦日益引起研究者的关注[7-11]，并且针对高层建筑、大跨桥梁等柔性结构的地震响应研究逐步深入[12-15]。杜永峰等[16]研究了近断层速度脉冲型地震动对RC框架结构构件的易损性；Shrestha等[18-19]分别研究了位于近断层区域尼泊尔Karnali斜拉桥和设置基础隔震装置的密苏里Bill Emerson Memorial斜拉桥的地震响应；丁幼亮等[20-22]研究了近断层脉冲地震动作用下大跨悬索桥的地震响应。已有研究主要存在两个问题：① 计算模型多采用固支，较少考虑土-结构相互作用(简称SSI效应)。诸如大跨缆索桥梁结构，其体系刚度不足，上部结构自重大，使得近断层地震动作用下基础下部土体变形较大。因此为准确分析大跨斜拉桥的地震响应，须考虑下部土体与结构之间的相互作用。② 未区分脉冲类型对结构不利响应的影响。随着对断层破裂机制认识的不断加深，学者们已关注到两类脉冲型地震动所引起结构响应的差异，然而，关于脉冲类型对大跨桥梁结构的影响规律尚缺乏足够的认识。

鉴于此，本文以苏通大桥为原型研究了大跨斜拉桥近断层脉冲地震动作用下的地震反应，基于太平洋地震工程研究中心强震数据库，选择近断层破裂前方效应和滑冲效应地震动，以及近场无速度脉冲地震动作为地震输入，并分析了3类地震动的频谱特性；采用系统化的集总参数模型表征地基土的动力特性，对比分析了大跨桥梁结构在主塔固支和考虑SSI效应时的动力特性，进一步研究了脉冲类型和SSI效应对主塔和主梁地震反应的影响规律，为近断层区域大跨径斜拉桥的抗震设计提供一定的参考。

1 地震动选取及反应谱特性分析

1.1近断层地震动选择及其特征参数

为分析近断层脉冲地震动对斜拉桥地震响应的影响，基于太平洋地震研究中心强震数据库选取破裂前方效应、滑冲效应及无脉冲地震动共30条，各地震动特性参数见表1。表中，PGA、PGV、PGD分别表示峰值地面加速度、峰值地面速度和峰值地面位移；PGV/PGA为表征速度脉冲效应的脉冲参数，PGV/PGA>0.2 s时速度脉冲较为显著，PGV/PGA<0.2 s时一般无明显脉冲现象，由表1可见，近场无脉冲地震动脉冲效应不显著。

1.2近断层地震动弹性反应谱分析

3组地震动运动特征存在显著的差异，有必要对其进行频谱特性分析。根据表1地震动分组，分别计算了各组地震动作用下3%阻尼比线弹性(μ=1)单自由度体系的弹性反应谱(地震动PGA均统一调整为0.3 g)，并求得各分组的平均反应谱。图1(a)和图1(b)分别为3组地震动作用下加速度和速度反应谱平均值。

(a) 谱加速度平均值

(b) 谱速度平均值

由图1分析可知：对于线弹性单自由度加速度反应谱，当体系周期T<1.2 s时，近场无速度脉冲谱加速度平均值明显高于脉冲地震动，各类型峰值加速度对应的周期均位于0.5 s附近，无脉冲地震动加速度峰值高于脉冲型地震动；当体系周期T>1.2 s时，脉冲型地震动仍具有较高的谱加速度值，且滑冲效应脉冲谱加速度值高于破裂前方效应脉冲，无脉冲地震动长周期成份不显著。对于速度反应谱，脉冲效应地震动谱速度明显高于无脉冲地震动，其中滑冲效应地震动谱速度最高，破裂前方效应地震动次之，无脉冲地震动最低。

表1 地震动分组及其特性参数

2 近断层地震动作用下斜拉桥地震响应分析

2.1研究对象

苏通大桥为主跨1 088 m的双塔双索面钢箱梁斜拉桥，是世界上跨径第二大斜拉桥。该桥主梁总宽为41 m，主塔呈倒Y形，塔高300.4 m，斜拉索呈扇形布置，边跨设置辅助墩(图2)。本文采用通用有限元软件ANSYS 16.0建立其动力计算的脊骨梁有限元模型(图3)，钢箱梁、主塔以及桥墩均采用弹性梁单元模拟；用空间梁单元定义刚臂，以确定拉索固定位置及主梁约束位置；用空间杆单元模拟拉索，考虑斜拉索的垂度效应；支座处耦合水平方向和竖直方向的位移。为了消除因网格划分不当对计算结果的影响，分别建立了5个单元数不同的全桥模型(单元数分别为533个、1 375个、2 661个、3 779个和5 021个)，并比较了前5阶振型频率随单元数目的变化趋势，综合考虑计算精度和计算时间等因素，确定了最优的单元数量，上部结构共2 661个单元，1 883个节点。近断层地震动沿全桥纵向和横向分别输入计算模型，不考虑竖向地震动的作用，且不关注行波效应的影响。本文建立了2种计算模型：塔底固支和考虑SSI效应模型。

注：A为边跨1；B为边跨2；C为边跨3；D为中跨

(b) 主塔墩基础

(a) 动力模型

(b) 土-结构相互作用模型

2.2简化土-结构模型及结构动力特性分析

强震作用下结构的基础会出现显著的位移，土-结构系统亦会出现非线性，在进行近断层地震响应分析时，SSI效应不容忽视。对于中小跨桩基桥梁，常采用六弹簧模型模拟土-结构相互作用[23]，该模型为线性系统，且不考虑土体的阻尼，在模拟大跨斜拉桥土-结构相互作用时不够精确。为此，不少学者提出了集总参数法，将大跨桥梁结构的地基简化为质量-弹簧-阻尼的非线性等效系统，用少量的集中参数表征地基的动力特性[24]，由于质量系统的存在，考虑SSI的结构抗震分析需考虑自由场的输入问题，使得计算变得复杂[25]。为了避免这一问题出现，Wu等[26]提出了系统化集总参数模型以准确表征地基土的动力特性，分别采用弹簧和阻尼器串联在主塔底部来表示土体的水平阻抗、竖向阻抗、摆动阻抗和扭转阻抗，从而避免了质量系统，在进行抗震分析时统一采用地表输入。集总参数模型是由多个与频率无关的阻尼器和弹簧按不同组合串联建立的一种非线性弹簧-阻尼系统，该系统中的弹簧和阻尼器均采用线性弹簧和阻尼。

苏通大桥主塔墩基础由131根长约120 m、间距6.75 m的钻孔灌注桩组成，承台为变截面、变厚度的“哑铃形”混凝土结构，平面尺寸为113.7 m×48.1 m(图2(b))。为了精确模拟土-结构效应的动力特性，本文采用多项式阶数为N=3的系统化集总参数模型模拟土-结构间相互作用(图3(b))，各弹簧和阻尼器系数的值分别为：

(1)

(2)

(3)

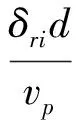
(4)

式中：d为基础特征宽度；vs为土体剪切波速；vp为土体剪切波速；γi、δi分别为土体阻抗的弹簧和阻尼器动态系数，根据Wu等给出的土体阻抗函数拟合得到，其值见表2；Khs、Kvs、Krs、Kts分别为水平、竖向、摇摆和转动静刚度，由方形基础静刚度及群桩静刚度组成，方形基础静刚度见式(5)：

(5)

式中：G为土的剪切模量；ν为土的泊松比。

为计入群桩对承台刚度的贡献，采用Budhu等[27]提出的桩顶自由时单桩刚度模式，通过叠加各单桩刚度并考虑群桩效率系数以得到群桩刚度贡献，见式(6)：

(6)

表2 集总参数模型格式化的弹簧和阻尼器系数

为简化计算，不考虑地基土的分层情况，地基土体材料主要参数定义为：密度1 700 kg/m3，泊松比0.33，剪切模量17 MPa，剪切波速150 m/s，压缩波速为300 m/s。基于上述有限元模型，采用子空间迭代法对该桥固结及考虑SSI效应两种模式分别进行自振特性分析。表3列出了前10阶振型频率及相关振型的特点。对上述前10阶频率和振型进行分析和比较可知，第1阶振型为主梁纵飘，符合该类桥型特点；由于该桥宽跨比较小，第2阶振型表现为主梁对称侧弯，且早于主梁对称竖弯出现；索塔侧弯振型从第7阶模态开始出现。考虑SSI效应后，由于结构变柔，整体刚度下降，各阶频率均有下降，相比于固结模型，SSI效应对纵向刚度影响最为显著，基频减小了27%；由于SSI效应改变了结构的动力特性，使得部分振型次序发生变化，如，二阶主梁反对称竖弯早于一阶索塔侧弯。

2.3大跨径斜拉桥地震响应分析

为分析不同脉冲类型对大跨径桥梁结构响应的影响，将表1中各地震动记录分别输入上述两种计算模型，所选地震动PGA均统一调整为0.3 g，地震动输入方式采用纵桥向输入和横桥向输入两种，选取主塔和主梁的关键截面作为采样点，主要分析主塔位移、剪力和弯矩以及主梁位移和弯矩，取每组地震时程分析的平均值作为计算结果。

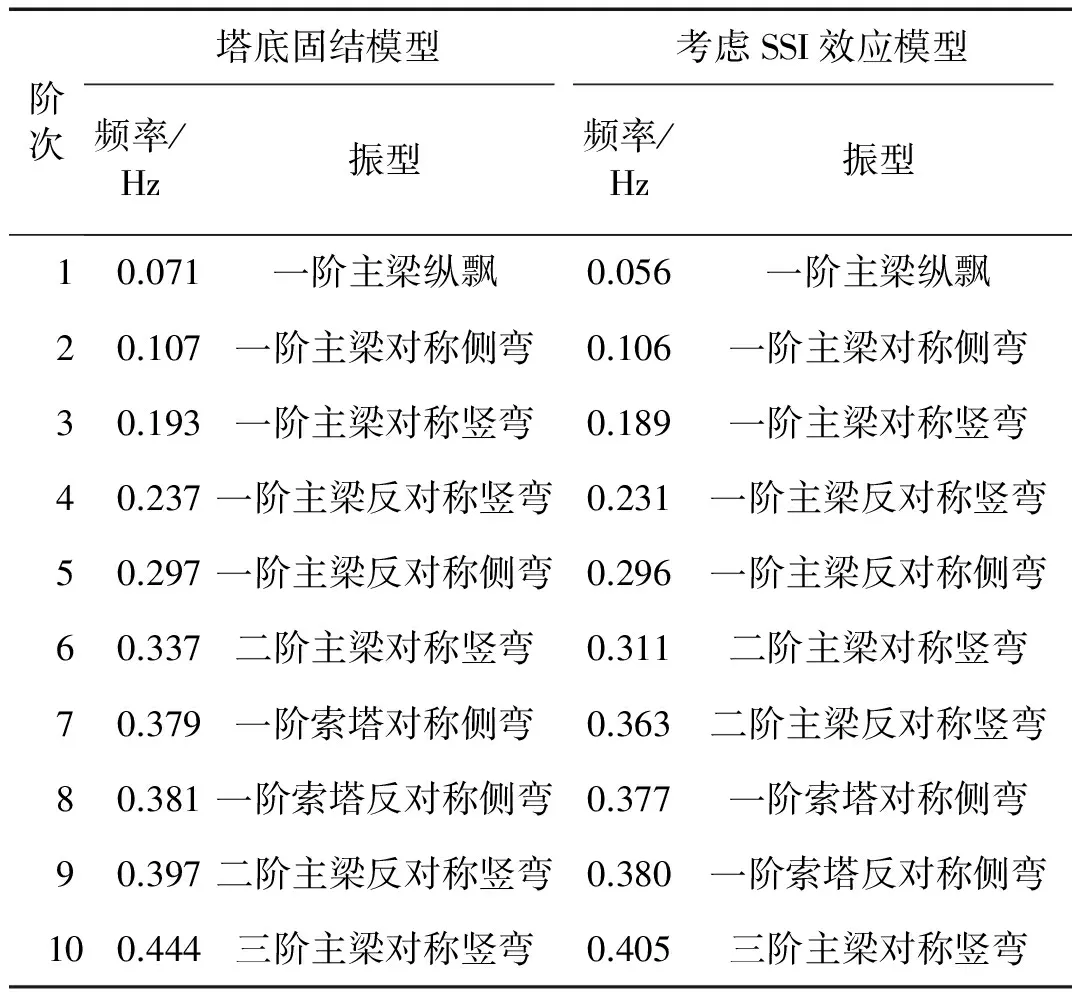
表3 斜拉桥动力特性对比

为了验证计算模型的有效性，采用地震工程专业模拟软件OPENSEES建立苏通大桥的塔底固结模型，选取典型的脉冲型地震动TCU052-NS作为地震纵向输入，对比两种软件建立模型的计算结果，如图4所示，ANSYS与OPENSEES建立模型的计算结果一致，其中塔顶位移的最大相对误差为6%，塔底弯矩的最大相对误差为2%。

(a)塔顶位移(b)塔底弯矩

图4 计算结果验证

Fig.4 Calculation result verification

2.3.1 近断层地震动作用下主塔响应分析

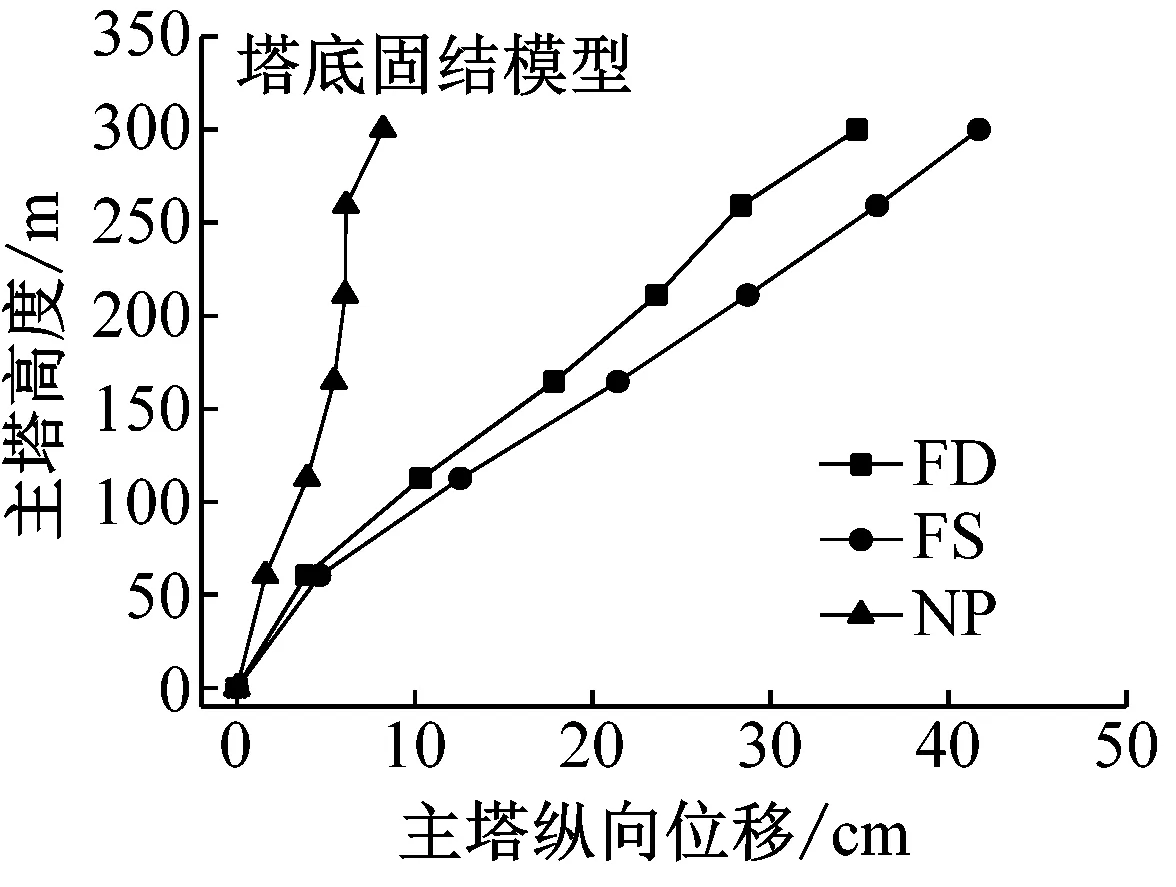
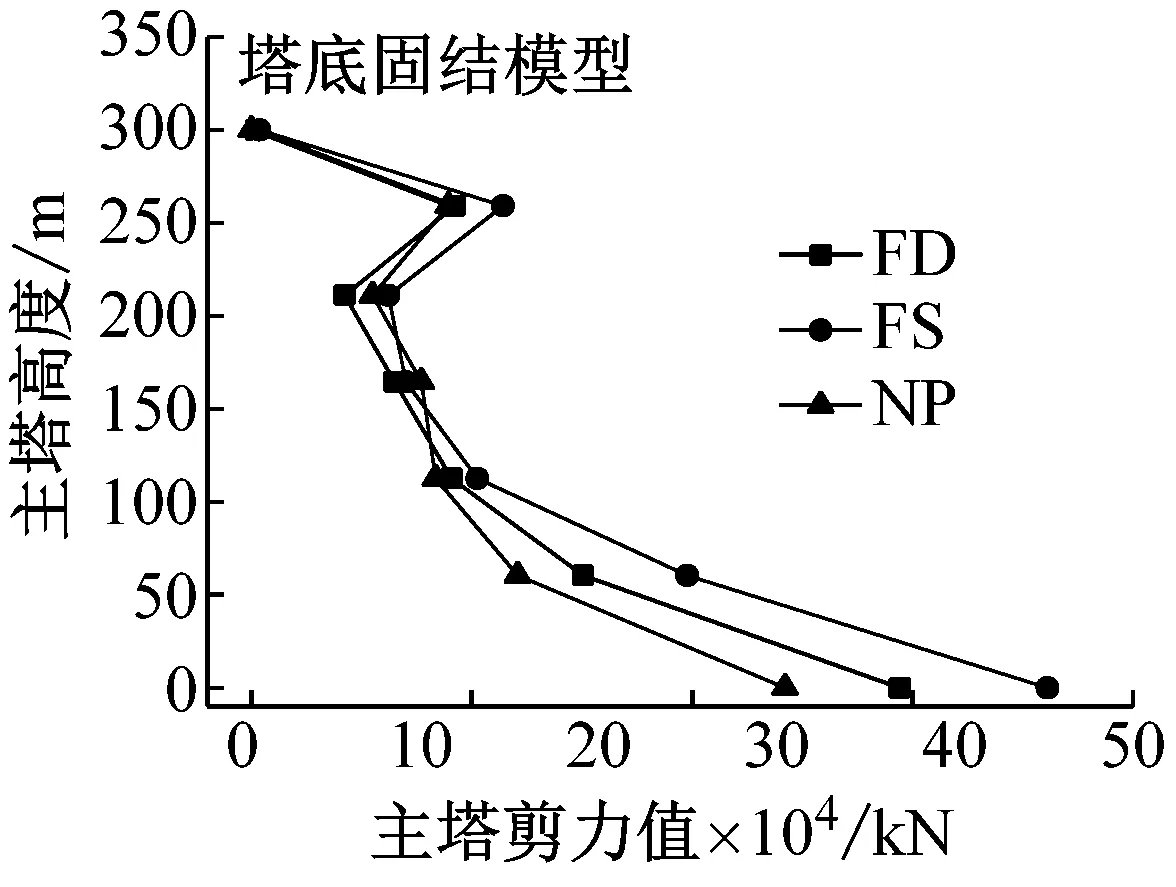
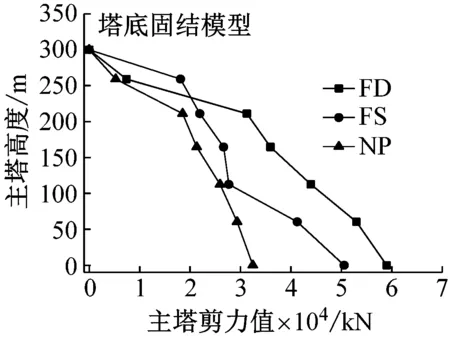
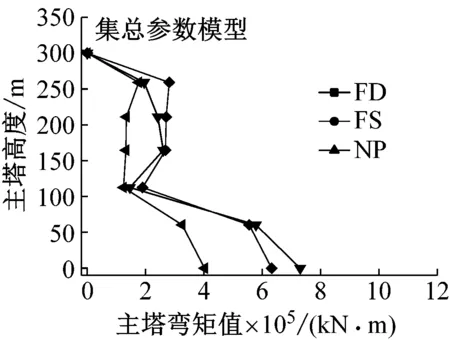
图5给出了在纵桥向地震激励下，该桥主塔纵向位移和内力的峰值包络曲线，图6为在横桥向地震激励下，该桥主塔横向位移和内力的峰值包络曲线。由图5和图6可见，随塔高增加，无论是纵桥向输入还是横桥向输入地震动，主塔变形均呈增大趋势，塔顶处变形最大，主塔内力总体呈下降趋势，在下塔柱易损部位，内力增长趋势较为显著，这对于以内力控制为主的结构抗震设计提出了更高的要求，而塔底处剪力和弯矩均为最大，符合桥塔受力特点。

(a) 主塔纵向位移

(b) 主塔剪力

(d) 主塔纵向位移

(e) 主塔剪力

(f) 主塔弯矩

(a) 主塔横向位移

(b) 主塔剪力

(d) 主塔横向位移

(e) 主塔剪力

(f) 主塔弯矩

由图5(a)可知，塔底固结模型在纵桥向激励下，破裂前方效应和滑冲效应地震动更容易激发桥塔的基本振型，而近场无脉冲地震动可激发桥塔的高阶振型。这是因为脉冲型地震动含有明显的长周期成份，破裂前方效应地震动的平均脉冲周期为5.8 s，而滑冲效应地震动的平均脉冲周期为8.8 s，此处平均脉冲周期是指对各脉冲型地震动脉冲周期(见表1)的算术平均值；同时大跨斜拉桥也是长周期结构，影响主塔纵向变形的一阶纵飘振型周期(对应主塔反对称纵弯)为14.6 s，一阶主梁对称竖弯(对应主塔对称纵弯)振型周期为5.17 s，而脉冲周期介于两者之间，其较易引起桥塔的基本振型；而近场无脉冲地震动无长周期成份，并且其包含丰富的高频成份，考虑到桥塔高阶振型的自振周期均集中于短周期阶段，因此其可激发桥塔的高阶振型。

由图6(a)可见，塔底固结模型在横桥向激励下，破裂前方效应激发桥塔的基本振型，滑冲效应和近场无速度脉冲地震动则激发桥塔的高阶振型，这是由于影响主塔横向变形的主塔侧弯振型出现在第7阶振型，周期为2.64 s，与破裂前方效应地震动的脉冲周期相近，易激发其基本振型，而滑冲效应地震动的脉冲周期与之相差较大，其高频成份起主导作用，同样近场无脉冲地震动因不含长周期成份，其短周期作用效应较为显著，因此滑冲效应和近场无速度脉冲地震动均激发了桥塔的高阶振型。类似的分析亦适用于考虑SSI效应模型(图5(d)和图6(d))，该效应延长了结构的各阶周期，导致部分脉冲效应地震动亦可能激发主塔的高阶振型，例如图6(d)所示，横桥向激励时，两类脉冲效应地震动均可明显激发主塔高阶振型。此处需指出，因地震动频谱特性的不同，不同地点的地震动引起结构地震响应亦存在差异，但具有长周期效应的脉冲地震动是引起主塔振动呈基本振型的主要因素。

由图5和图6可见，纵桥向激励时，相比于固结模型，考虑SSI效应后不同脉冲类型地震动作用下斜拉桥上塔柱变形及内力均变化较小；中塔柱及下塔柱位移显著增大，如破裂前方效应(FD)、滑冲效应(FS)和无脉冲地震动作用下中塔柱底纵向位移分别增加了1.42、1.30和1.09倍；而内力均出现一定程度的降低，其中下塔柱内力下降最为显著，如塔底剪力和弯矩均分别降低了21%及54%以上。横桥向激励时，破裂前方效应地震动作用下，SSI效应可显著降低主塔剪力及弯矩，但对其变形影响较小，相较于塔底固结模型，主塔剪力和弯矩分别下降了10%和39%；滑冲效应地震动作用下，SSI效应可显著增大主塔变形，降低主塔剪力，但中塔柱及上塔柱的弯矩值略有增大，下塔柱弯矩出现明显降低，相较于塔底固结模型，主塔位移最大提高29%，而下塔柱弯矩下降28%。综上，纵桥向激励时，SSI效应可显著放大中塔柱及下塔柱纵桥向变形；横桥向激励时，滑冲效应和SSI效应共同作用下可明显放大主塔横向变形；SSI效应可显著降低下塔柱内力。

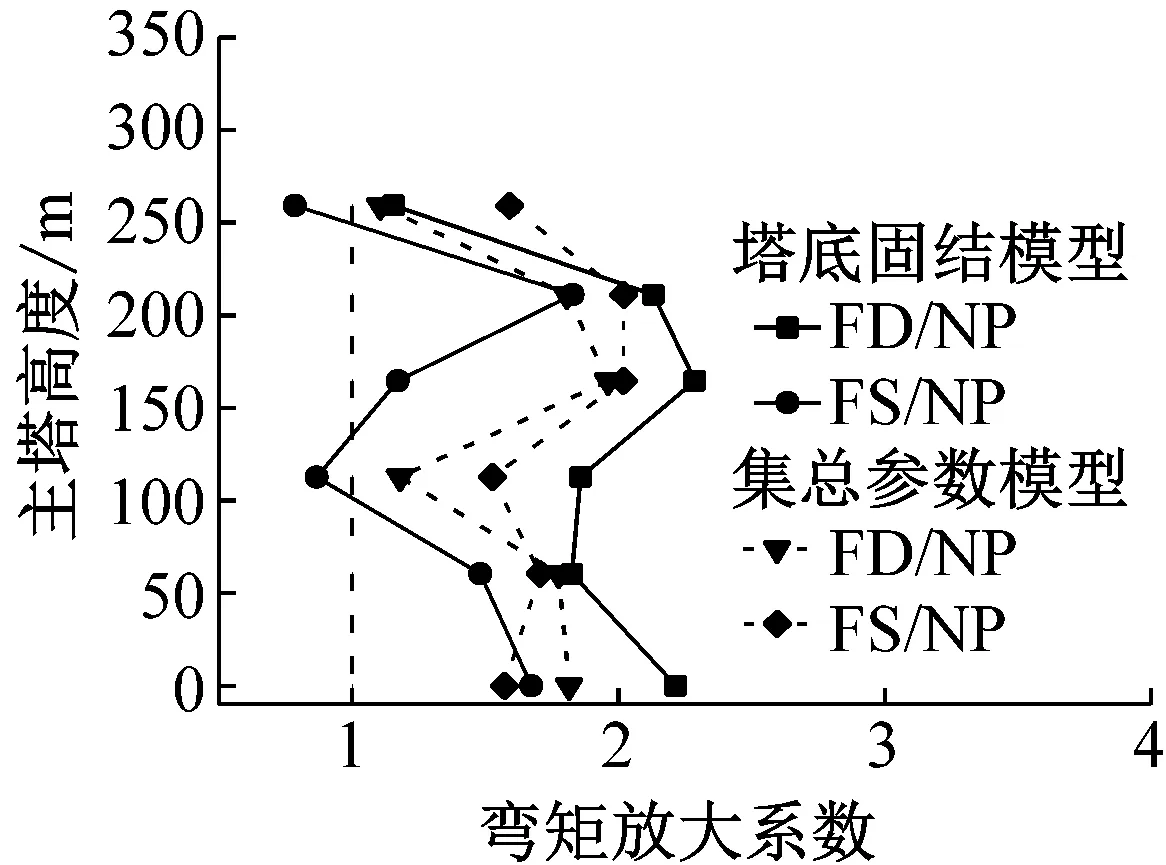
为了量化脉冲地震动和无脉冲地震动作用下大跨斜拉桥地震反应的差异，定义脉冲效应放大系数=脉冲型地震动反应幅值/近断层无脉冲地震动反应幅值。图7和图8分别为纵桥向激励和横桥向激励下主塔响应的脉冲效应放大系数曲线。进一步比较脉冲地震动和无脉冲地震动作用下大跨斜拉桥地震反应的差异，可见，塔底固结时，纵桥向激励下破裂前方效应(滑冲效应)地震动对桥塔纵向位移、纵向剪力和纵向弯矩的最大放大系数分别为4.6(5.8)、1.2(1.6)和1.8(2.0)；横桥向激励下破裂前方效应(滑冲效应)地震动对桥塔横向位移、横向剪力和横向弯矩的最大放大系数分别为4.0(3.3)、1.8(1.6)和2.3(1.8)。考虑SSI效应模型，亦可见相似规律。综上，脉冲地震动对主塔位移及内力均具有明显放大效应，其中对主塔位移尤为显著。

(a) 主塔纵向位移

(b) 主塔剪力

(a) 主塔纵向位移

(b) 主塔剪力

进一步分析可得，不同脉冲类型地震动对大跨斜拉桥地震响应的影响亦存在差异，如塔底固结时，在纵桥向输入下(图7)，滑冲效应地震动引起结构响应均大于破裂前方效应地震动，相较于破裂前方效应地震动，滑冲效应地震动引起塔顶位移、塔底剪力和弯矩分别增大了22%、21%和10%；而在横向输入下(图8)，破裂前方效应地震动引起结构地震响应均大于滑冲效应地震动，相较于滑冲效应地震动，破裂前方效应地震动引起塔顶位移、塔底剪力和弯矩分别增大了6%、16%和33%。这是由于影响斜拉桥纵向地震响应的振型主要为第一阶主梁纵飘振型和第三阶主梁对称竖弯振型，从速度反应谱(图1(b))可以看出，位于这两阶周期处的滑冲效应地震动的平均速度反应谱值远大于破裂前方效应地震动；而影响斜拉桥横向地震响应的振型主要为第七阶主塔对称侧弯振型，位于其周期处两种脉冲效应的速度反应谱值相近，且在此周期以前，破裂前方效应地震动的速度反应谱谱值略大于滑冲效应地震动。因此，破裂前方效应地震动易于影响斜拉桥横向响应，而滑冲效应地震动对斜拉桥纵向响应更加敏感。分析考虑SSI效应的桥梁模型地震响应规律，由于结构周期的延长及高阶振型的变化，纵桥向激励下(图7)，两类脉冲地震动对结构响应的影响较为接近；横桥向激励下(图8)，破裂前方效应地震动引起下塔柱内力高于滑冲效应地震动，而滑冲效应地震动会引起主塔更大的横向位移。

2.3.2 近断层地震动作用下主梁响应分析

为研究近断层效应及SSI效应对斜拉桥主梁地震响应的影响规律，分别给出了纵桥向激励下主梁竖向位移和弯矩沿纵桥向峰值变化曲线(图9)和横桥向激励下主梁横向位移和弯矩沿纵桥向的峰值变化曲线(图10)，对应纵桥向和横桥向地震输入下主梁响应的脉冲效应放大系数曲线分别示于图11和图12。

在纵桥向激励下，由图9(a)可见，主梁位移峰值曲线呈两边小中间大的趋势，边跨3竖向位移最大，中跨竖向位移次之，这是因为该区域相对刚度(跨径300 m)较主跨(1 088 m)高，可能导致该区域自振周期更接近于脉冲地震动的卓越周期；由图9(b)可见，主梁弯矩包络曲线呈两边大中间小的趋势，边跨弯矩更为显著，该现象是因为边跨跨径较小且设置压重，使得边跨相对刚度要高于中跨。在横桥向激励下，由图10(a)可见，中跨横向位移最大，边跨横向位移较小；由图10(b)可见，主塔处的主梁横向弯矩最大，这是由于主塔对主梁横向有很大的约束作用，使得此处弯矩最大。

由图9可见，纵桥向激励下，相比于固结模型，SSI效应造成主梁竖向位移及弯矩值均出现一定程度的降低，其中脉冲地震动降低较为显著，在滑冲效应和破裂前方效应地震动作用下，SSI效应使得跨中竖向位移分别下降了30.34%和22.01%，但边跨1最大弯矩处下降并不明显，分别降低了12.36%和6.69%。

(a) 主梁竖向位移

(b) 主梁弯矩

Fig.9 The maximum response along the length of the girder under longitudinal excitation

(a) 主梁横向位移

(b) 主梁弯矩

Fig.10 The maximum response along the length of the girder under horizontal excitation

由图10可见，横桥向激励下，SSI效应和脉冲效应共同作用下，主梁横向位移明显增大，其中破裂前方效应地震动作用下，主梁跨中横向位移增大了35.45%，滑冲效应地震动作用下，边跨1横向位移增大了33.5%，但无脉冲地震动作用时，SSI效应降低了主梁横向位移，其中跨中横向位移下降了69.5%； SSI效应可明显增大主梁的横向弯矩，破裂前方效应地震动作用下主塔处主梁横向弯矩增大42%，滑冲效应地震动作用下边跨侧辅助墩处主梁横向弯矩增大45.5%，无脉冲近断层地震动作用下主塔处主梁横向弯矩增大18%。

综上所述，近断层地震动作用下SSI效应对主梁纵向响应是有利的，但SSI效应和脉冲效应共同作用下可明显放大主梁横向响应，抗震设计中提高横桥向主梁设计标准。此外，总体趋势上，滑冲效应地震动引起主梁地震响应大于破裂前方效应地震动，这是由于主梁竖弯振型和主梁侧弯振型周期都接近滑冲效应地震动脉冲周期，使得滑冲效应地震动对主梁的影响更强。显然脉冲地震动显著增加了主梁动力响应。

由脉冲效应放大系数(见图11和12)可清晰反映出脉冲地震动和无脉冲地震动作用下主梁地震响应的差异，主塔固结时，在纵桥向激励下，破裂前方效应和滑冲效应地震动对主梁竖向位移的最大放大系数分别为3.3和4.2，其中边跨3跨中的主梁竖向位移放大效应最为显著，放大系数分别为4.7和7.2；对主梁弯矩的平均放大系数为2.9和3.3，主塔处的主梁弯矩放大效应最为显著，放大系数为4.0和5.4，考虑SSI效应时主梁纵桥向响应规律与塔底固结模型类似。在横桥向激励下，桥塔固结时，相较于无脉冲地震动，破裂前方效应和滑冲效应地震动对主梁横向位移最大放大系数分别为1.9和2.3；考虑SSI效应时，对模型主梁横向位移最大放大系数为4.7和6.2，对应中跨跨中截面；横桥向地震作用下脉冲型地震动对主梁横向弯矩的平均放大系数分别为1.3和1.2，可见脉冲地震动对主梁横向弯矩影响并不显著。

(a) 主梁竖向位移

(b) 主梁弯矩

Fig.11 Response amplification coefficient curve of the girder under longitudinal excitation

(a) 主梁横向位移

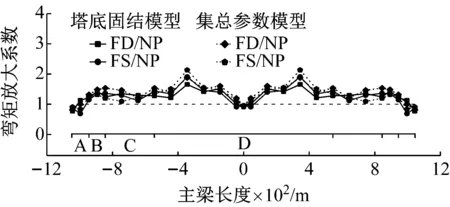
(b) 主梁弯矩

Fig.12 Response amplification coefficient curve of the girder under horizontal excitation

3 结论

本文以苏通大桥为研究对象，采用系统化的集总参数模型表征地基土的动力特性，建立考虑SSI效应的结构动力数值计算模型，选取破裂前方效应脉冲、滑冲效应脉冲和无脉冲三组近断层地震动作为地震输入，计算分析了近断层脉冲效应和土-结构相互作用(SSI效应)对大跨斜拉桥地震响应，在此基础上以脉冲地震动反应幅值与无脉冲地震动反应幅值的比值作为放大系数，进一步研究了脉冲效应和SSI效应对大跨斜拉桥地震响应的影响规律，得到了以下结论：

(1)脉冲效应地震动脉冲周期与主梁纵飘、主梁竖弯振型周期接近，纵桥向激励下主要激发桥塔的基本振型；破裂前方效应地震动脉冲周期与主塔侧弯振型周期接近，横桥向激励下易于激发桥塔的基本振型，而滑冲效应地震动脉冲周期与主塔侧弯振型周期相差较大，主要激发桥塔的高阶振型；无脉冲地震动无长周期成份，主要激发桥塔的高阶振型。

(2)考虑SSI效应时，脉冲地震动作用下主塔位移较塔底固结模型最大增加了42%，主塔内力最多减小50%；纵桥向地震激励时，SSI效应可降低主梁位移及弯矩，但横桥向激励时，SSI效应和脉冲效应共同作用下可明显放大主梁横桥向响应。可见在近场区域大跨斜拉桥抗震设计时，SSI效应对横桥向和纵桥向响应影响规律不同，须重点关注。

(3)脉冲效应地震动引起斜拉桥地震响应明显高于无脉冲地震动，其中位移增幅最高可达7.2倍，内力增幅最高可达5.4倍。在纵桥向地震激励下，滑冲效应地震动对主塔响应影响最大，而在横桥向激励下，破裂前方效应地震动对主塔响应影响更加显著；在纵向或横向激励下，滑冲效应地震动对主梁响应的影响都更加明显。故近场区域抗震设计中，应考虑脉冲效应对长周期结构的不利影响，选取或合成具有不同脉冲类型的脉冲型地震动进行结构抗震验算，保证工程结构的安全。

近断层地震动对长周期结构地震响应影响显著，而近断层脉冲型地震动记录相对匮乏，加之桥梁结构体系丰富多样，今后还需考察更多的地震记录以及研究不同结构体系的桥梁在近断层脉冲型地震动作用下的地震响应规律，以完善现有抗震设计理论和方法，确保工程结构的安全。

[1] 谢文，孙利民. 采用新型辅助墩的超大跨斜拉桥顺桥向损伤控制新体系研究[J]. 土木工程学报，2014，47(2):28-34.

XIE Wen, SUN Limin. Studies on controlling structural systems of super long-span cable-stayed bridge by novel supporting pier in longitudinal direction[J]. China Civil Engineering Journal, 2014, 47(2):28-34.

[2] 刘洪兵，朱晞. 大跨度斜拉桥多支承激励地震响应分析[J]. 土木工程学报，2001，34(6):38-44.

LIU Hongbing, ZHU Xi. Seismic response analysis of long span cable stayed bridges under multi support excitations[J]. China Civil Engineering Journal, 2001, 34(6):38-44.

[3] 叶爱君，范立础. 超大跨度斜拉桥的横向约束体系[J]. 中国公路学报，2007，20(2):63-67.

YE Aijun, FAN Lichu. Lateral constraint systems for super-long-span cable-stayed bridge[J]. China Journal of Highway and Transport, 2007, 20(2):63-67.

[4] ABDEL-GHAFFAR A M, NAZMY A. 3-D nonlinear seismic behavior of cable-stayed bridges[J]. Journal of Structural Engineering, 1991, 117(11):3456-3476.

[5] SONEJI B B, JANGID R S. Influence of soil-structure interaction on the response of seismically isolated cable-stayed bridge[J]. Soil Dynamics & Earthquake Engineering, 2008, 28(4):245-257.

[6] ATMACA B, YURDAKUL M, SEVKET A. Nonlinear dynamic analysis of base isolated cable-stayed bridge under earthquake excitations[J]. Soil Dynamics & Earthquake Engineering, 2014, 66:314-318.

[7] BRAY J D, RODRIGUEZ-MAREK A. Characterization of forward-directivity ground motions in the near-fault region[J]. Soil Dynamics & Earthquake Engineering, 2004, 24(11):815-828.

[8] SOMERVILLE P G, SMITH N F, GRAVES R W, et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J]. Pakistan Journal of Statistics & Operation Research, 1997, 68(1):199-222.

[9] 刘彦辉，谭平，金建敏，等. 地震作用下全浮漂大跨斜拉桥耗能减震控制研究[J]. 振动与冲击，2015，34(8): 1-6.

LIU Yanhui. TAN Ping, JIN Jianmin, et al. Energy dissipation control for long span cable-stayed bridge adopting floating system under earthquake[J]. Journal of Vibration and Shock, 2015, 34(8): 1-6.

[10] 余友熙，刘中华，余香林，等. 基于非线性随机最优控制的大跨度斜拉桥地震响应Benchmark问题研究[J]. 振动与冲击，2016，35(8): 42-47.

YU Youxi, LIU Zhonghua, YU Xianglin, et al. Benchmark problem investigation for seismic response of large span cable-stayed bridge based on nonlinear stochastic optimal control[J]. Journal of Vibration and Shock, 2016, 35(8): 42-47.

[11] 陈令坤，张楠，胡超，等. 近断层地震方向脉冲效应对高速铁路桥梁弹塑性反应的影响[J]. 振动与冲击，2013，32(15): 149-167.

CHEN Lingkun, ZHANG Nan, HU Chao, et al. Effects of near-fault directivity pulse-like ground motion on elastic-plastic seismic response of high-speed railway bridge[J]. Journal of Vibration and Shock, 2013, 32(15): 149-167.

[12] KALKAN E, KUNNATH S K. Effects of fling step and forward directivity on seismic response of buildings[J]. Earthquake Spectra, 2006, 22(2): 367-390.

[13] 江义，杨迪雄，李刚. 近断层地震动向前方向性效应和滑冲效应对高层钢结构地震反应的影响[J]. 建筑结构学报，2010，31(9): 103-110.

JIANG Yi, YANG Dixiong, LI Gang. Effects of forward directivity and fling step near-fault ground motions on seismic responses of high-rise steel structure[J]. Journal of Building Structures, 2010, 31(9): 103-110.

[14] WU G, ZHAI C, LI S, et al. Effects of near-fault ground motions and equivalent pulses on Large Crossing Transmission Tower-line System[J]. Engineering Structures, 2014, 77: 161-169.

[15] YANG D, PAN J, LI G. Interstory drift ratio of building structures subjected to near-fault ground motions based on generalized drift spectral analysis[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(11): 1182-1197.

[16] 韩淼，张文会，朱爱东，等. 不同层隔震结构在近断层地震作用下动力响应分析[J]. 振动与冲击，2016，35(5): 120-124.

HAN Miao, ZHANG Weihui, ZHU Aidong, et al. Dynamic response analysis for multi-story structures with different isolation stories under near-fault ground motions[J]. Journal of Vibration and Shock, 2016, 35(5): 120-124.

[17] 李帅，王景全，颜晓伟，等. 近断层地震动空间分布特征对斜拉桥地震响应影响[J]. 土木工程学报，2016，49(6):1-11.

LI Shuai, WANG Jingquan, YAN Xiaowei, et al. Influence of spatial distribution characteristics of near-fault ground motions on seismic response of cable-stayed bridges[J]. China Civil Engineering Journal, 2016, 49(6):1-11.

[18] SHRESTHA B. Seismic response of long span cable-stayed bridge to near-fault vertical ground motions[J]. KSCE Journal of Civil Engineering, 2015, 19(1): 180-187.

[19] ISMAIL M, CASAS J R, RODELLAR J. Near-fault isolation of cable-stayed bridges using RNC isolator[J]. Engineering Structures, 2013, 56(6):327-342.

[20] 丁幼亮，谢辉，耿方方，等. 近断层地震动作用下多塔悬索桥的地震反应分析[J]. 工程力学，2015，32(7): 38-46.

DING Youliang, XIE Hui, GENG Fangfang. Seismic response analysis of a multi-tower suspension bridge subjected to near-fault ground motions[J]. Engineering Mechanics, 2015, 32(7): 38-46.

[21] CAVDAR O. Probabilistic sensitivity analysis of two suspension bridges in Istanbul, Turkey to near-and far-fault ground motion[J]. Natural Hazards & Earth System Science, 2012, 12(2):459-473.

[22] ADANUR S, ALTUNIIK A C, BAYRAKTAR A, et al. Comparison of near-fault and far-fault ground motion effects on geometrically nonlinear earthquake behavior of suspension bridges[J]. Natural Hazards, 2012, 64(1): 593-614.

[23] 叶爱君，管仲国. 桥梁抗震[M]. 2版. 北京：人民交通出版社，2011：72-73.

[24] WANG H, LIU W, ZHOU D, et al. Lumped-parameter model of foundations based on complex Chebyshev polynomial fraction[J]. Soil Dynamics & Earthquake Engineering, 2013, 50(7):192-203.

[25] 王曙光，杜东升，刘伟庆. 土-结构相互作用对消能减震结构损伤谱的影响[J]. 土木工程学报，2015，48(4): 84-90.

WANG Shuguang, DU Dongsheng, LIU Weiqing. Influence of soil-structure interaction on damage spectra of passive energy dissipation structures[J]. China Civil Engineering Journal, 2015, 48(4): 84-90.

[26] WU W H, LEE W H. Systematic lumped-parameter models for foundations based on polynomial-fraction approximation[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(7): 1383-1412.

[27] DAVIES T G, BUDHU M, DAVIES T G. Non-linear analysis of laterally loaded piles in heavily overconsolidated clays[J]. Géotechnique, 1986, 36(4):527-538.

Effectsofnear-faultpulse-typegroundmotionsontheseismicresponsesofalong-spancable-stayedbridge

ZHANGFan1,2,LIShuai1,2,YANXiaowei3,WANGJingquan1,2

(1. Key Laboratory of Concrete and Prestressed Concrete Structure of China Ministry of Education, Nanjing 210096, China; 2. National Prestress Engineering Research Center, Nanjing 210096, China; 3. Shanghai Municipal Planning Design Research Institute, Shanghai 200040, China)

The objective of the study is to determine the seismic responses of the Sutong cable-stayed bridge, taking into account the near-fault pulse-type ground motion effect and soil-structure interaction effect(SSI). Systematic lumped-parameter models were adopted to describe the dynamic behavior of the foundation supported on soil. The dynamic finite element model of the bridge considering the SSI effect was established. The seismic responses of the towers and deck subjected to three pulse-type ground motions, i.e. forward-directivity effect pulse (FD), fling-step effect pulse (FS) and non-pulse records, were investigated. The results reveal that SSI effects mainly affect the bridge responses through a systematic decrease of all modal frequencies and a substantial change in the nature of dominant shapes especially for the higher modes of vibrations. When the bridge is subjected to pulse-type near-fault ground motions, the SSI effect causes larger displacements of the towers, a significant decrease in the internal forces of the towers, and a certain degree of reduction in both the displacement and base moment of the girder under longitudinal excitations. However, the response of the girder under horizontal excitations is obviously amplified by the SSI effect. The seismic responses of the cable-stayed bridge under the pulse-type ground motions are significantly higher than that under non-pulse ground motions. Fling-step ground motions amplify the responses of the towers under longitudinal excitations and the responses of the girder under longitudinal or horizontal excitations. Forward-directivity ground motions amplify the responses of the towers under horizontal excitations. The research results could provide a reference for the seismic design of long-span cable-stayed bridge systems located in near-fault zones.

near-fault ground motion; forward-directivity effect; fling-step effect; systematic lumped-parameter model; soil-structure interaction; long-span cable-stayed bridge

U448.27

10.13465/j.cnki.jvs.2017.21.025

国家自然科学基金(51378110)；江苏省“六大人才高峰”第十一批(JZ-007)；江苏省研究生科研创新计划(KYLX15_0086)

2016-04-11 修改稿收到日期：2016-08-23

张凡男，博士生，1991年生

王景全男，博士，教授，博士生导师，1976年生。E-mail:wangjingquan@seu.edu.cn