光镊模型的矢量衍射矩阵化方法与应用研究

张冠鸣，谭勇

（长春理工大学 理学院，长春 130022）

光镊模型的矢量衍射矩阵化方法与应用研究

张冠鸣，谭勇

（长春理工大学 理学院，长春 130022）

光镊是生物物理以及生物工程领域的一种重要工具，光镊模型及其求解是目前的一个研究重点。根据矢量散射的基本原理和米氏散射作用，提出了一种将矢量衍射方程矩阵化的方法，该方法把经过透镜汇聚的入射光束进行平面波分解，结合米氏散射公式与旋转变换，然后导出了散射光场的矩阵形式，最后将该矩阵应用于模拟计算米氏散射的光场。此方法不限制光束的波长，不但简化了运算难度，也获得了与无散射情况下的矢量衍射计算、有散射情况下的瑞利近似计算各自相同的结果。本文的研究方法可应用于具有一定大小粒子的散射计算，为进一步控制光镊行为提供了依据。

矢量衍射；米氏散射；光镊

在生物物理以及生物工程领域，光镊是用来操纵分子的一种重要工具。它利用涡旋光束的辐射作用和粒子的散射效应来操纵分子［1-2］，在DNA分子的操作、细胞的夹取和成像中均有重要应用［3］。在之前的文章中，研究了瑞利条件下粒子在涡旋光束下的行为，但当粒子的尺寸接近光束波长时，瑞利近似会带来很大的误差。而米氏散射的计算又很复杂。为此提出了一种将矢量衍射方程矩阵化方法，并应用于米氏散射的光场计算。将透镜汇聚的入射光分解，旋转变换，照射到球形粒子后进行散射叠加，具体设计了相应的算法并对算法进行了验证，避免了复杂方程的求解，简化了计算复杂度。在实际应用中为进一步控制光镊行为提供了理论依据。

1 矢量衍射方程的矩阵化

依据基尔霍夫衍射定理，在一般情况下，透镜汇聚光束的电场矢量和磁场矢量衍射方程可以分别描述为［4］：

其中，f是焦距，i是虚数单位，而公式中fi(θ,φ)和gi(θ,φ)分别代表透镜对平面波波矢量和偏振方向的旋转，在笛卡尔坐标上分别表示为：

公式（1）和（2）分别描述了透镜对电场和磁场的会聚作用。此时，平面波经过透镜前后的单位波矢量分别用k̂0和k̂1代表，而旋转前和旋转后波矢量的夹角称之为旋转的角度，相应的合成矢量为旋转矢量，如图1所示。

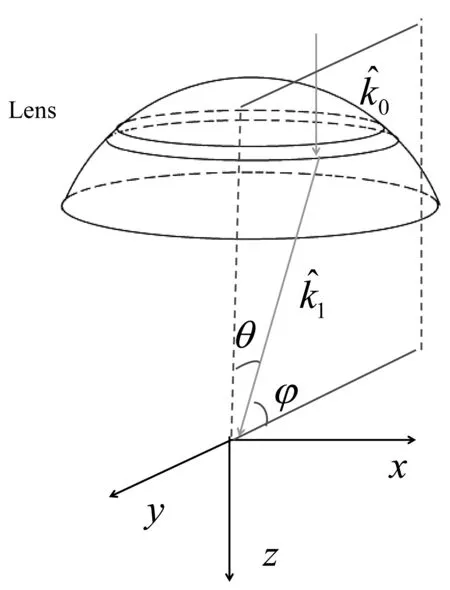
图1 透镜汇聚示意图

如果平面波在均匀电中性介质中传播再到达透镜，经过透镜前的单位波矢量可写为：

通过透镜出射后的波矢量为：

旋转矢量为：

而旋转的角度为：

带入到旋转矩阵中［5］

得到：

令电场的偏振方向为x方向，经过旋转后存在：

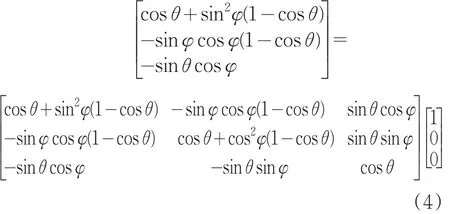
经过三角函数变换之后可以得出积分公式（1）中的fi(θ,φ)与公式（4）表征的向量是相等向量，该向量表示为：

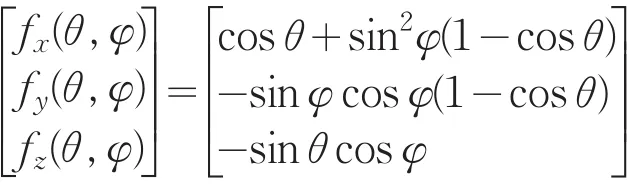
故而可以将积分公式写成如下形式（假定磁场的偏振方向是y方向）：

将衍射公式改写为矩阵形式以后将有利于米氏散射场的计算。

2 矢量衍射光场的米氏散射

米氏散射可直接求解平面波的亥姆霍兹方程，得出在电中性介质中的散射光场球坐标表达式，得出的电场和磁场可表示为级数求和［6］。设定入射平面波电场的偏振方向为x轴，磁场的偏振方向为y轴，波矢量方向为z轴，并在此基础上建立球坐标系。结合矢量衍射和米氏散射，计算任意光束经过透镜会聚后产生的散射场。利用方程的线性性质和旋转变换方法，避免重新求解亥姆霍兹方程，简化计算步骤和复杂程度。为了表示方便，定义电场E⇀经过球形物体的米氏散射后变为，这是一个线性变换算符，散射后的电场为：

为了得到散射场，先看一下米氏散射公式（1）和（2）使用的坐标系（图2和图3），米氏散射的坐标系为X1，Y1，Z1坐标系，Z1平行于波矢量而电场与X1轴平行。求得的米氏散射的电场也是在X1，Y1，Z1坐标下的表示。

图2 米式散射所使用的坐标系

将所有结果表示在图2和图3所示的xyz坐标系统中，首先将（X1，Y1，Z1）坐标平移至透镜的焦点，通过相应的坐标变换得到的散射场就是在（X，Y，Z）坐标下的表示，对任意向量有：

公式（7）是一个被动坐标变换，电场不参与变换，只是相应坐标改变了。而公式（6）中旋转矩阵［Mrot］是主动变换，也就是对电场本身的旋转。值得注意的是，公式（6）也需要经过坐标变换，但其中的θ,φ分别是波矢量与Z轴负方向的夹角，波矢量在xy平面的投影与x轴的夹角，并不受平移变换的影响。

3 计算和结果

3.1 算法

将矢量衍射方程矩阵化并应用于米氏散射后，设计了相应的算法进行模拟计算，具体算法如下：

（1）离散化球坐标r,θi,φi，并定义网格

（2）计算（X1，Y1，Z1）坐标表示下的离散米氏散射场

（3）将其转换为直角坐标

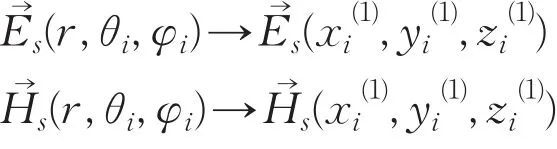
（4）坐标变换到（x，y，z）坐标系

（5）旋转电磁场

（6）带入公式（6）进行数值积分，即可得到在半径为R的球形粒子散射场。

3.2 算法验证

下面将通过两种特殊情况验证以上算法：

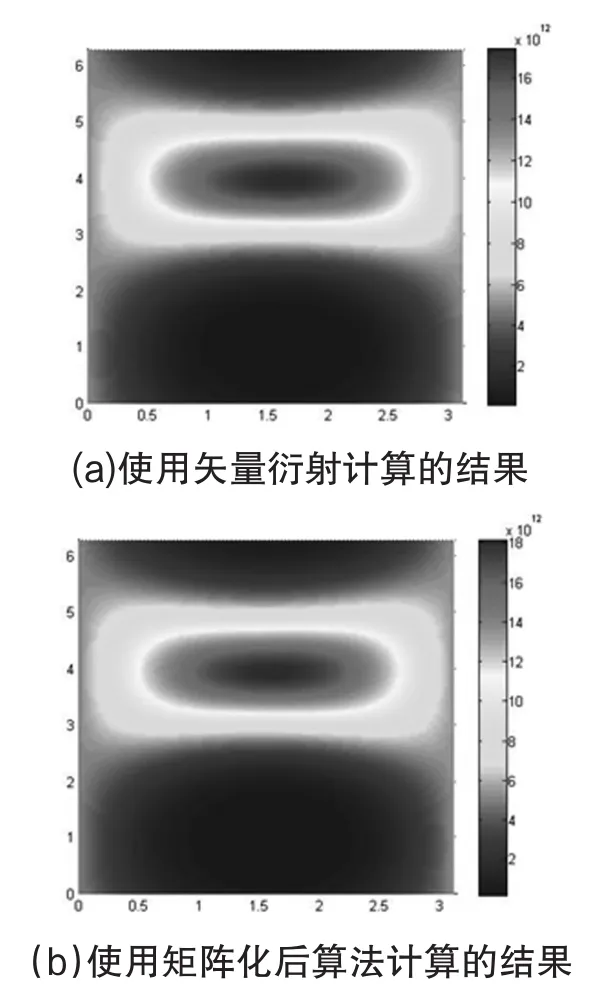
图4 无散射情况下光强分布

图5 当粒子半径远小于入射波长时光强分布

从图4和图5的结果可以看出，矢量衍射方程矩阵化，对粒子有无散射场均起到了有效模拟计算效果。无散射场时粒子衍射光强主要在以θ≈1.6rad、φ≈4rad区域附近，光场呈近矩形分布；而有米氏散射和瑞利散射场的粒子，被光场捕获时，除了θ≈1.5rad、φ≈3rad中心区域，还存在其他分离区域的光场分布，并且，中心区域的散射光场的角度位置相对于无散射场略有微小偏移，整个散射光场图形向近椭圆演化。这样的结果与涡旋电场及其偏振机制有很大的关联。

4 结论

为了研究各种光束及散射粒子光镊的性质，依据矢量衍射方程，针对无散射场、有米氏散射和瑞利散射场的粒子被光镊捕获这两种情况，模拟了涡旋光场场强分布。由于瑞利散射条件和平行轴近似的限制，大多数情况下的散射场和受力很难得出。然而，如此复杂的模型和高难度计算，通过将矢量衍射方程矩阵化，再应用于米氏散射计算模型，不但简化了运算难度，也获得了与无散射情况下的矢量衍射计算、有散射情况下的瑞利近似计算各自相同的结果。证明了这种矢量衍射方程矩阵化的正确性和高效率。以后的工作将继续集中在：分别针对普通均匀分布的光束和涡旋光束，用这一方法模拟光镊的行为，提高研究准确性和效率。

［1］Mas J，Farre A，Cuadros J，et al.Understanding optical trapping phenomena：a simulation for undergraduates［J］.IEEE Transactions on Education，2011，54（1）：133-140.

［2］任智斌，姜会林，付跃刚，等，微球体与微椭球体光散射特性的研究［J］.长春理工大学学报：自然科学版，2006，29（1）：28-31.

［3］Lang M J，Block S M.Laser-basedoptical tweezers［J］.American.Journal of Physics，2003，71（3）：201-215.

［4］Richards B，Wolf E，Electromagnetic diffraction in optical systems.II.Structure of the image field in an aplanatic system［J］.Mathematical and Physical Sciences，1959，253（1274）：358-379.

［5］Taylor C J，Kriegman D J.Minimization on the Lie group SO（3） and related manifolds［M］.Yale University，1994.

［6］Bohren C F，Huffman D R.Absorption and scattering of light by small particles［M］.Wiley，New York，2008：83-129.

［7］Jackson J D.Classical electrodynamics［M］.3rd ed.Wiley，New York，1975：456-462.

The Study on Method and Application about the Vector Diffraction Matrix of Optical Tweezers

ZHANG Guanming，TAN Yong
（School of Science，Changchun University of Science and Technology，Changchun 130022）

Optical tweezers are an important tool in biophysical and bioengineering fields which model and solution are the main research points recently.According to the basic principle of vector scattering and Mie scattering effect，a vector diffraction equation matrix method is proposed in this paper where a plane wave decomposition is done after it went through the lens and is combined with Mie scattering formula and rotation transform.Finally the matrix was applied to simulation of the Mie scattering field.This method does not restrict the wavelength of the light beam.It does not only simplify the calculation difficulty，but also get the same vector diffraction calculation results as other two methods including of the vector diffraction calculation without and with Rayleigh approximation.The research method can be applied to the scattering calculation of particles with a certain size，which provides a basis for further controlling the behavior of optical tweezers.

vector diffraction；Mie scattering；optical tweezers

O436.2

A

1672-9870（2017）05-0036-04

2017-08-12

张冠鸣（1992-），男，硕士研究生，E-mail：739863391@qq.com