容差模拟电路参数故障诊断

董海迪，刘 刚，何 兵，郑建飞，李红增

（1.火箭军工程大学空间工程系，陕西 西安 710025；2.火箭军工程大学控制工程系，陕西 西安 710025）

容差模拟电路参数故障诊断

董海迪1，刘 刚1，何 兵1，郑建飞2，李红增2

（1.火箭军工程大学空间工程系，陕西 西安 710025；2.火箭军工程大学控制工程系，陕西 西安 710025）

针对测试点有限条件下的容差模拟电路参数故障诊断问题，该文提出一种状态检测、故障隔离和状态验证及参数辨识的分步诊断策略。将容差电路的故障状态检测转化为线性规划方程最优解的存在性判断；采用Woodbury公式推导出不同电流源激励下测点处电压增量比值，将其作为故障特征，并证明容差条件下的电路故障特征值与标称参数下的仿真值是相同的；通过修正规划方程中疑似故障参数的偏差限，验证前期诊断结论的正确性并计算故障元件参数。直流、交流和非线性电路实例验证该理论的正确性和方法的有效性。该方法操作简单、可行性高，适用于大规模模拟电路的故障诊断和故障参数辨识。

模拟电路；容差；参数故障；线性规划

0 引 言

模拟电路故障诊断是电路设计和分析的重要研究内容[1-2]，主要包括故障状态检测、故障元件隔离和故障参数辨识。针对不同类型电路，国内外学者开展了大量相关故障诊断方法研究[3-11]。其中，故障字典法是最具代表性的方法，应用广泛且最具有实用价值[12-14]，但很少有文献对软故障和容差电路给出系统而有效的处理方法[15-17]，故其应用受到限制。

文献[12]提出一种基于SVC的混合故障字典法，采用符号决策机制缩减测试时间。文献[13]提出一种多特征故障字典模型，用Monte-Carlo分析得到阈值计算检测率与隔离率。文献[14]采用mRMR原则提取响应信号特征，遗传算法优化SVM核参数。文献[15]采用正态商分布推导了容差条件下斜率故障特征变化范围公式。文献[16]以节点电压增量比矢量为故障特征隔离故障元件。文献[17]采用微粒群优化方法诊断容差模拟电路单软故障。在测点有限条件下，如何辨识容差模拟电路参数故障仍然是亟待解决的问题[18]。

本文提出了一种基于线性规划方法和故障字典法的模拟电路故障诊断策略。首先将容差电路的故障状态检测转化为线性规划方程最优解的存在性判断；而后提取不同电流源激励下测点处的电压增量比值作为故障特征，进行故障隔离；最后通过修正规划方程中疑似故障参数的偏差限，验证前期诊断结论的正确性并计算故障元件参数。

1 故障特征提取

线性模拟电路N施加电流源激励b，采用节点方程描述该电路[19-20]，得到：

其中：e=[e1，…，en]T——节点与零点电势差；

b——电流源向量；

Yn——节点导纳矩阵。

假设节点k和l间元件导纳由Ykl变为Ykl+ΔYkl，扰动电路用表示，采用Woodbury公式[21]计算扰动电路导纳逆（Yn+ΔYn）-1，得到节点电压增量：

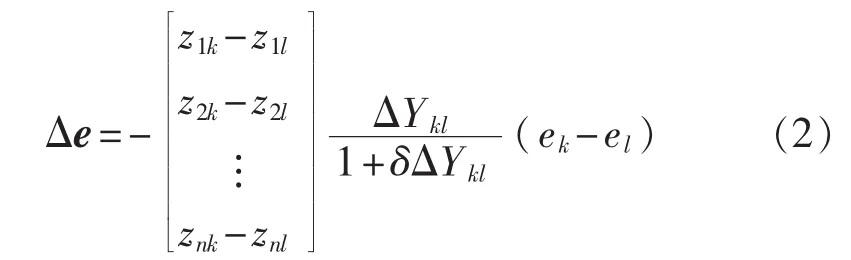
其中δ=zkk-zkl-zlk+zll，zij为阻抗矩阵Zn中的元素。

由式（2）和式（3）得到：

Δep、Δe（1）p——第p个测点处的电压增量。

2 容差条件下故障诊断

2.1 故障状态检测

采用参数 Xkl（Rkl/Ckl/Lkl）和参数增量 ΔXkl（ΔRkl/ΔCkl/ΔLkl）表征其导纳增量，得到：

考虑单个元件参数在容差范围内扰动，对应ΔXkl→0。将式（5）带入式（2），得到：

考虑电路中所有元件参数容差，得到：

式中：yi——测点i处测量电压与标称值间偏差；

xj——元件j的参数偏差；

aij——测点i处电压ei对元件j的电压灵敏度。

采用相量复数表征交流电路测点电压及偏差，式（7）修正为

式中：Re（·）、Im（·）——取复数实部、虚部运算；

dei/dXj——测点i处电压ei对参数Xj的电压灵敏度。

采用节点电压方程描述非线性电路，得到：

式中：x=[x1，…，xn]T——n个元件参数；

u=[u1，…，um]T——m个测点处的输出电压；

f（x）=[f1（x），…，fm（x）]T——测点输出电压与元件参数的函数，其数学表达式无法准确得到。

将f（x）在标称参数xnom处泰勒展开，忽略二次以上高次项，得到：

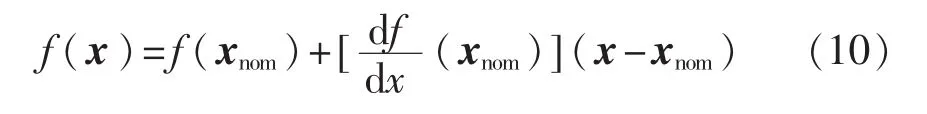
将式（10）带入式（9），得到形如式（7）等式：

其中aij表示测量电压ui对参量xj的电压灵敏度。

采用单纯形法[22]判断式（12）解的存在性。引入人工变量zi，得到辅助方程：

当式（13）存在最小目标值Z≈0，表示电路中未发生参数故障；当式（13）无解或最小目标值Z＞0，表示电路中存在参数故障元件。

2.2 故障元件隔离

实际电路中元件参数存在容差，式（4）不会严格成立，所有的元件端电压νkl也无法通过有限测点测量得到。

假设ΔYkl表示元件Ykl的实际值与标称值间偏差（在容差范围内），由式（2）得到 νkl和增量：

由式（4）得到：

考虑所有元件参数容差时，式（15）保持成立。因此得出结论：容差条件下的故障特征值与标称参数下的特征值相同。

由式（15）可知，将不同电流源激励下的电路测点处电压增量比值与标称参数下的故障特征值比对，即可隔离出故障元件。考虑电路元件较多时，存在大量故障特征值，测点处电压增量比值与故障特征值越接近，则对应元件发生故障的可能性越大。采用式（16）计算sp指数来衡量电路中元件发生故障的可能性，sp越小表示元件p发生故障的可能性越大。

式中：ep、e（1）p——电路最近一次无故障状态测量值；

2.3 故障状态验证及偏差量估计

采用2.2节的故障字典法隔离出故障元件后，需进一步进行故障验证。当元件发生故障时，对疑似故障元件k参数偏差上下限值εk+和-εk-进行修正。若修正后的方程存在最小目标值Z≈0，则表示元件k确实发生故障，对应k-εk-表示故障元件的参数偏差量。考虑到式（6）成立条件是元件参数偏差变化较小，因此假定本文方法能诊断线性电路元件参数偏差在30%以内的参数故障，则（-εk-，εk+）修正为（-γk-，γk+），式（13）修正为

2.4 故障诊断算法

在激励点和测试点有限条件下，对模拟电路的参数故障进行诊断，采用故障状态检测、故障元件隔离和故障状态验证及参数辨识的分步诊断方法，算法步骤如下：

1）标准输出电压和参数灵敏度获取及故障字典构建。对于拓扑结构、标称参数已知的电路，在PSPICE环境下对标准参数电路N进行仿真。分别给电路N施加电流源激励b和b（1），得到标准输出电压参数灵敏度和节点电压计算故障特征值并建立故障字典。

3）故障元件隔离。采用式（16）对所有元件发生故障概率由大到小进行排序，得到集合序列d。

4）故障状态验证及偏差估计。逐次选取d中元素，采用2.3节方法进行故障状态验证，直至找到故障元件并对其参数偏差进行估计，诊断结束。

3 实例验证

3.1 线性直流电路

采用文献[19]中线性直流电路，如图1所示。假设所有元件参数容差在标称值5%内，分别在激励点1和3处施加幅值为1 A的直流源激励，在测点1、2、3处测量电压。考虑以下几种状态：

状态1（容差条件下无故障）：电路中各元件参数取 值 R1=1.05 Ω，R2=1.96 Ω，R3=2.04 Ω，R4=4.08 Ω，R5=0.96Ω。

状态 2（无容差条件下 R1故障）：R1=1.2Ω，其余参数取值为标称值。

状态 3（容差条件下 R1故障）：R1=1.2Ω，其余参数取值与状态1中相同。

状态 4（无容差条件下 R3故障）：R3=1.85 Ω，其余参数取值为标称值。

状态 5（容差条件下 R3故障）：R3=1.85 Ω，其余参数取值与状态1中相同。

状态 6（无容差条件下 R4故障）：R4=4.8Ω，其余参数取值为标称值。

状态 7（容差条件下 R4故障）：R4=4.8Ω，其余参数取值与状态1中相同。

表1 电路故障字典

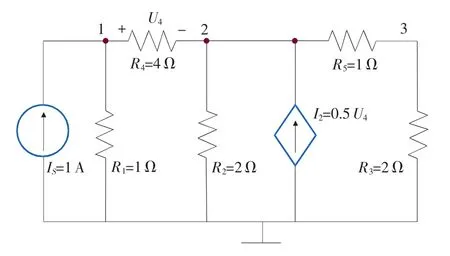
图1 线性直流电路

该电路构建故障字典如表1所示。从中可以看出，元件R1～R5对应的特征值νkl/ν（1）kl相互间差异很大，能够很容易利用故障特征值对故障元件进行隔离。

不同状态下测点处电压增量比值如表2所示。从中可以看出，不考虑容差情况（状态 2、4、6），测点 1、2、3处电压差增量比值 Δep/Δe（1）p与故障字典中故障元件特征值匹配，能够准确隔离出故障元件；容差条件下（状态3、5、7），选用标准参数下的ep和e（1）p，测点1、2、3处的电压差增量比值 Δep/Δe（1）p与故障元件特征值差别显著，无法进行故障元件隔离；选用容差条件下非故障状态的实测值ep和e（1）p， 测点1、2、3处的电压差增量Δep/Δe（1）p与故障元件特征值匹配，能够准确隔离出故障元件。

不同状态下计算得到元件参数增量与实际值对比如表3所示。从中可以看出，本文提出方法能够很好地对故障元件偏差量进行估计，具有较高辨识准确度。

表2 不同状态下各测点处电压增量比值

表3 不同状态下元件参数增量计算结果与实际值对比

图2 线性交流电路

3.2 线性交流电路

采用文献[20]中线性交流电路，如图2所示。假设所有元件参数容差在其标称值5%内，分别在1、4、8点施加频率10kHz，幅值为5，0.5，0.5mA的交流电流源激励，同时在1、4、8测点处测量电压。考虑容差条件下几种状态：

状态1（无故障）：电路中各元件参数取值为R1=9.9kΩ，R2=10.5kΩ，R3=195kΩ，R4=289kΩ，R5=726Ω，R6=39 kΩ，R7=59.5 kΩ，R8=10.5 kΩ，R9=11.4 kΩ，R10=3.76 kΩ，R11=59.9 kΩ，R12=40 kΩ，R13=3.54 kΩ，C14=1.04nF，C15=49nF，C16=4.8nF，C17=22.6 nF，C18=4.9 nF。式（13）存在最小目标值Z=0.0004，因此得出电路无故障结论。

状态 2（R2故障，R2=8.5kΩ）。式（13）无解，取 d中前 3 项（R2、R10、R14），采用 2.3 节方法排除了其他元件，诊断出R2发生故障，计算参数值为R2=9.1kΩ。

状态 3（R7故障，R7=50kΩ）。式（13）无解，取 d 中前 3 项（R7、R9、R6），采用 2.3 节方法排除了其他元件，诊断出R7发生故障，计算参数值为R7=46.4kΩ。

状态 4（C16故障，C16=6nF）。式（13）无解，取 d 中前 3 项（C16、C15、R10），采用 2.3 节方法排除了其他元件，诊断出C16发生故障，计算参数值为C16=6.1nF。

状态 5（C18故障，C18=6.2nF）。式（13）无解，取 d中前 3 项（C18、R6、R7），采用 2.3 节方法排除了其他元件，诊断出C18发生故障，计算参数值为C18=6.1nF。

3.3 非线性直流电路

采用文献[20]中非线性直流电路，如图3所示。假设所有元件参数容差在其标称值5%内，分别在激励点2和7施加幅值为1mA的直流源激励，在测点1、2、7处测量电压。考虑容差条件下几种状态：

图3 非线性直流电路

状态1（无故障）：电路中各元件参数取值为R1=101kΩ，R2=27.5kΩ，R3=100Ω，R4=690Ω，R5=9.9kΩ，R6=21.8 kΩ，R7=10.1 kΩ，R8=4.75 kΩ，R9=1 kΩ，R10=10Ω。式（13）存在最小目标值Z=0.0014，因此得出电路无故障结论。

状态 2（R4故障，R4=810 Ω）。式（13）无解，取 d中前 3 项（R5、R4、R7），诊断出 R4发生故障，计算参数值为R4=838Ω。

状态 3（R5故障，R5=11.5kΩ）。式（13）中 Z=0.195，取 d 中前 4 项（R9、R7、R4、R5），诊断出 R5发生故障，计算参数值为R5=11.1kΩ。

状态 4（R8故障，R8=4kΩ）。式（13）中 Z=1.44，取d中前1项（R8），诊断出R8发生故障，计算参数值为R8=3.93kΩ。

状态 5（R9故障，R9=800 Ω）。式（13）无解，取 d中前 4 项（R7、R9、R4、R5），诊断出 R9发生故障，计算参数值为R9=786Ω。

4 结束语

本文提出了一种有限测点条件下容差模拟电路参数的故障诊断方法。首先对电路故障状态进行检测，将测点处输出电压增量与元件参数偏差函数转化为容差约束下的线性规划问题，从而将电路故障检测转化为线性规划问题最优解存在性求解；然后采用Woodbury公式推导出不同电流源激励下测点电压增量比值，将其可作为故障特征，并证明容差条件下的电路故障特征值与标称参数下特征值相同；最后通过修正疑似故障元件偏差限值，检测修正后电路故障状态，验证前期诊断结论正确性，并计算故障参数偏差。仿真电路实验表明，该方法操作简单，具有较高的诊断准确度和参数辨识准确度，能够很好地解决有限测点和容差条件下的模拟电路参数故障诊断。

[1]KABISATPATHY P， BARUA A， SINHA S.Fault diagnosis of analog integrated circuits[M].Germany：Springer Verlag，2005：5.

[2]GIZOPOULOS D.Advances in electronic testing：challenges and methodologies[M].Germany：Springer，2006：3.

[3]CUI Y， SHI J， WANG Z.Analog circuits fault diagnosis using multi-valued Fisher’s fuzzy decision tree（MFFDT）[J].International Journal of Circuit Theory and Applications，2016，44（1）：240-260.

[4]邓勇，于晨松.因子分析和ELM在模拟电路故障诊断的应用[J].电子测量与仪器学报，2016，30（10）：1512-1519.

[5]MAKINO T， HAYASHI T， WATANABE M.New aspects of fault diagnosis of nonlinear analog circuits[J].International Journal of Electronics and Telecommunications，2015，61（1）：83-93.

[6]郭栋梁，刘新妹，殷俊龄，等.通用电路板自动故障诊断系统的设计与实现[J].中国测试，2016，42（7）：112-116.

[7]周启忠，谢永乐.基于矩阵扰动的模拟电路故障诊断方法[J].西南交通大学学报，2017，52（2）：369-378.

[8]唐小峰，许爱强，李文海.多层次模拟电路随机变异生成方法研究[J].中国测试，2016，42（1）：12-15，64.

[9]裴杰才，李志华，丁伟聪.基于混合核函数PSO-SVM的模拟电路故障诊断[J].计算机与现代化，2017（1）：41-45，56.

[10]AMINIAN M，AMINIAN F.A modular fault-diagnostic system for analog electronic circuits using neural networks with wavelet transform as a preprocessor[J].IEEE Transactions on Instrumentation and Measurement，2007，56（5）：1546-1554.

[11]BHUNIA S， RAYCHOWDHURY A， ROY K.Defect oriented testing of analog circuits using wavelet analysis of dynamic supply current[J].Journal of Electronic Testing，2008，21（2）：147-159.

[12]崔江，王友仁.一种新颖的基于混合故障字典方法的模拟故障诊断策略[J].电工技术学报，2013，28（4）：272-278.

[13]李旻，王彩利，龙兵，等.多特征故障字典及其在模拟电路可测性分析中应用[J].电子测量与仪器学报，2015，29（3）：368-374.

[14]孙健，王成华.基于mRMR原则和优化SVM的模拟电路故障诊断[J].仪器仪表学报，2013，34（1）：221-226.

[15]敖永才，师奕兵，张伟，等.基于正态商分布的模拟故障容差处理新方法[J].仪器仪表学报，2013，34（3）：698-706.

[16]叶笠，王厚军，田书林，等.容差模拟电路软故障诊断的一种方法[J].电工技术学报，2011，26（5）：119-125.

[17]周龙甫，师奕兵，李焱骏.容差条件下PSO算法诊断模拟电路单软故障方法[J].计算机辅助设计与图形学学报，2009，21（9）：1270-1274.

[18]杨士元.模拟电路故障诊断与可靠性设计[M].北京：清华大学出版社，1993：2.

[19]TADEUSIEWICZ M，KORZYBSKI M.A method for fault diagnosis in linear electronic circuits[J].International Journal of Circuit Theory and Applications，2000，28（3）：245-262.

[20]TADEUSIEWICZ M， HALGAS S， KORZYBSKI M.An algorithm for soft-fault diagnosis of linear and nonlinear circuits[J].IEEE Transactions on Circuits and Systems I： Fundamental Theory and Applications，2002，49（11）：1648-1653.

[21]HOUSEHOLDER A S.The theory of matrices in numerical analysis[M].New York：Blaisedell Publishing Company，1965：185-188.

[22]SIERKSMA G.Linear and integer programming:theory and practice[M].Florida：CRC Press，2001：64-65.

（编辑：商丹丹）

Parameter fault diagnosis on analog circuits with tolerance

DONG Haidi1， LIU Gang1， HE Bing1， ZHENG Jianfei2， LI Hongzeng2
（1.Department of Space Engineering，Rocket Force University of Engineering，Xi’an 710025，China；2.Department of Automation Engineering，Rocket Force University of Engineering，Xi’an 710025，China）

Focusing on the fault diagnosis with limited test points on analog circuits with tolerance， a stepwise diagnosis strategy for fault detection， fault isolation， state verification and parameter identification is put forward.Firstly，a linear programming concept is developed to transform fault detection of circuit with limited accessible terminals for measurement to check existence of a feasible solution under tolerance constraints.The Woodbury formula is deduced under different excitation current source measuring point voltage increment ratio as the fault feature，and prove that the simulation circuit fault tolerance characteristics under the condition of value and nominal values are the same.Lastly， fault detection of the circuit with revised deviation restriction for suspected faulty components is proceeded to locate faulty element and estimate its parameter.Correctness of the theory and effectiveness of the proposed method are verified by DC，AC and nonlinear circuit experimental results.The proposed method is simple and feasible and suitable for large-scale analog circuits fault diagnosis and fault parameter identification.

analog circuit； tolerance；parameter fault；linear programming

A

1674-5124（2017）09-0128-06

10.11857/j.issn.1674-5124.2017.09.023

2017-02-11；

2017-04-09

国家杰出青年基金项目（61025014）；国家自然科学基金项目（61403399）

董海迪（1988-），男，湖北武汉市人，博士研究生，研究方向为模拟电路测试与故障诊断。