钳压法制作的同轴电缆法布里-珀罗传感器

刘 嘉， 焦 彤， 周 智，2， 肖 海

（1.大连理工大学土木工程学院，辽宁 大连 116024；2.大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024；3.克莱姆森大学电子与计算机工程系，南卡罗来纳州 克莱姆森市 29630）

钳压法制作的同轴电缆法布里-珀罗传感器

刘 嘉1， 焦 彤1， 周 智1，2， 肖 海3

（1.大连理工大学土木工程学院，辽宁 大连 116024；2.大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024；3.克莱姆森大学电子与计算机工程系，南卡罗来纳州 克莱姆森市 29630）

为研究同轴电缆法布里-珀罗干涉（CCFPI）传感器的钳压法制作工艺，模拟不同结构参数对CCFPI传感器信号质量的影响，分析得出CCFPI反射点的绝缘层外径宜在1.4～2mm范围内，钳压变形长度不应小于2mm，反射点一致性对信号质量影响显著；模拟电缆拉伸过程，观察到信号频移对电缆应变呈现良好的线性反应。依据模拟结果制作CCFPI传感器，并进行传感性能测试。试验结果表明：CCFPI传感器测得的应变值始终与千分表吻合良好，二者拟合斜率为1.00492，相关系数为0.99867，且在小应变范围内CCFPI传感器的测量数据与光纤光栅吻合良好，说明该传感器的测量结果真实可靠；同时观察到CCFPI传感器的分辨率可达110με，失效应变为140000με。

同轴电缆；法布里-珀罗传感器；钳压法；优化设计；大应变测量

0 引 言

结构在长期服役过程中受到环境腐蚀、材料老化、荷载长期效应的影响，产生损伤累积，在极端情况下可能发生灾难性事故[1]。因而，对重大结构进行实时监测诊断，预测结构性能变化，做出维护决定，具有重大意义[2]。

传感器处于健康监测系统的最前端，对测量的精确度起到决定作用[3]。而土木工程的实际应用要求传感器具有大变形测量能力和良好的传感性能，并且能够适应恶劣的工作环境。同轴电缆凭借材料坚固、抵抗电磁干扰、价格低廉等诸多优点进入研究视野。20世纪末，同轴电缆电时域反射技术（electrical time domain reflectometry，ETDR）开始用于土木工程领域：Dowding C H等[4]将同轴电缆用于监测岩体变形；Miau B S[5]将同轴电缆嵌入混凝土中探测结构内部的断裂破坏；Lin M W等[6]将同轴电缆研制成混凝土裂纹传感器；Kane W F[7]将同轴电缆用于滑坡监测。

随后，基于相似的电磁场理论机制，光纤传感器的优异概念在同轴电缆中得到应用，实现了同轴电缆布拉格电栅（coaxial cable bragg grating，CCBG）传感器的制作及钢筋混凝土梁的应变监测[8-10]。Hai Xiao等[11]率先提出并发展了同轴电缆法布里-珀罗干涉（coaxial cable Fabry-Perot interferometer，CCFPI）传感原理，并验证了CCFPI传感器的应变测量能力，为其应用研究奠定了理论基础；Trontz A等[12]用不锈钢管和钢丝作为外导体和内导体，氧化铝陶瓷作为绝缘层重构同轴电缆，研制出CCFPI高温监测传感器。上述CCFPI传感器的研究主要聚焦于传感机理分析与应变解算方法，而想要将其用于结构健康监测的工程实践仍需开展大量工作。本文从CCFPI传感器工程化应用的角度出发，提出钳压法制作工艺，通过仿真模拟分析钳压法制作CCFPI传感器的性能影响因素，实现优化设计，并对CCFPI传感器进行封装保护，试验验证其用于应变监测的可行性，为工程化应用研究提供器件基础。

1 CCFPI传感器的变形感知机理

同轴电缆由共用同一轴心的内导体、绝缘层、外导体和护套四部分构成（如图1所示），其特性阻抗由自身参数决定[13]：

式中：Z0——同轴电缆的特性阻抗；

a、b——同轴电缆内导体的直径和外导体的内径；

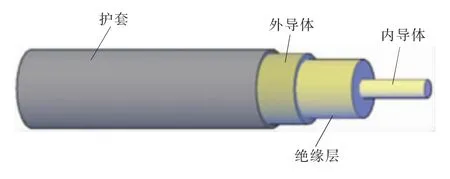
图1 同轴电缆结构示意图

εr——同轴电缆绝缘层的相对介电常数。

由此可知，同轴电缆的特性阻抗与内外导体的尺寸以及绝缘层的介电常数有关，通过钳压控制电缆外径或通过钻孔改变绝缘层的介电常数可制作阻抗不连续点，使电缆中传输的电磁波发生反射，而两个阻抗不连续点即构成法珀腔。已有试验结果表明，通过挤压套在电缆上的软质金属管可以使电缆产生局部变形，制成反射点，并且这种方法对电缆结构的破坏较少，对电缆机械强度的削弱较小，因而本文针对钳压法制作的CCFPI传感器进行分析，传感器示意图如图2所示。

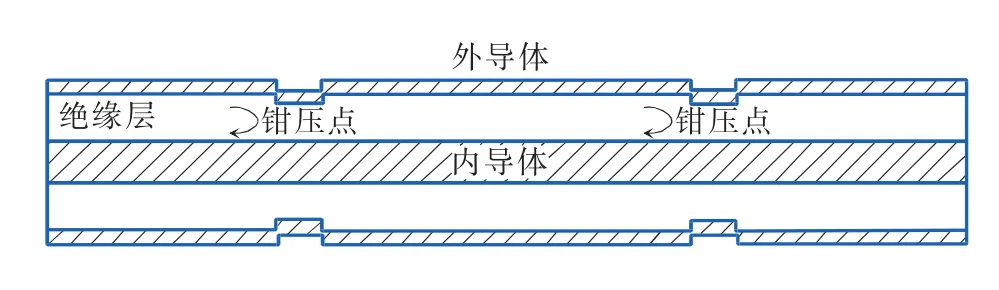
图2 CCFPI传感器示意图

在同轴电缆上制作两个弱反射点，忽略两点间的多次反射，将两点的反射波由于接收延时产生的干涉近似看作双波干涉。延时长短与反射点间距及绝缘层的相对介电常数存在如下关系：

式中：τ——两反射波的延时；

d——两反射点的间距；

c0——光在真空中传播的速度。

当外界温度发生变化或电缆承受应变时，反射点间距d随之改变，从而影响两反射波的接收延时τ，使干涉谱发生频移。

由电磁学原理，干涉谱的第N阶谐振频率为

相应的第N阶频移为

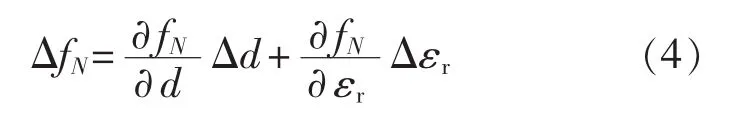
由于光弹效应，电缆伸长会引起绝缘层的相对介电常数减小，具体关系如下：

式中Peff为同轴电缆绝缘层的有效电光系数。

将式（5）代入式（4），可得出应变 ε 与频移 ΔfN的关系如下：

因此，若fN和Peff已知，则可以通过测量干涉频谱第N阶谐振频率的频移ΔfN计算电缆的应变ε，从而实现CCFPI传感器的应变测量。

2 CCFPI传感器的仿真分析

采用ANSYS HFSS软件进行仿真分析，由于电磁波的传输存在集肤效应，近似认为同轴电缆的内外导体均为理想导体，将内导体的材料属性选为PEC，令绝缘层的外表面与背景直接关联自动定义为理想导体边界，省略外导体的建模，以此对模型进行合理简化，加快计算速度。

模型尺寸依照SF141型号电缆的结构参数（如表1所示）设置，内导体直径为0.92 mm，绝缘层外径为2.98 mm，材质为聚四氟乙烯（材料属性选用Teflon）；模型长度为140mm。求解频点采用LinearCount方式设置，起始频率为45 MHz，终止频率为8GHz，频点个数为16001。

表1 SF141型号同轴电缆的结构参数

2.1 不同结构参数对干涉频谱的影响

采用钳压法制作CCFPI传感器需要确定钳压变形程度、钳压变形长度、钳压间距3个结构参数。一般而言，钳压程度越大，钳压长度越长，反射信号越强。本文采用控制变量法模拟不同结构参数对干涉频谱的影响，确定合理结构参数的范围，从而为CCFPI传感器的优化设计提供参考。

1）钳压变形程度的影响

当钳压间距为80 mm，反射点钳压变形长度为2 mm，绝缘层外径以0.2 mm步距由2.4 mm变化至1.4 mm，由图3可知，绝缘层外径越小（即钳压变形程度越大），干涉频谱的峰值越高，图谱形状愈加规整，但是当绝缘层外径由1.6mm变化到1.4mm时，波峰发生轻微展宽，可能是因为当钳压变形增大到一定程度后，阻抗变化区的几何长度（2mm）难以继续近似看作单一的反射点，其对反射信号的影响将不可忽略。此外，可以看出，当绝缘层外径在1.4～2mm范围内，信号质量较好。

图3 钳压变形程度对干涉频谱的影响

2）钳压变形长度的影响

当钳压间距为80mm，反射点绝缘层外径为2mm，钳压变形长度以2 mm步距由2 mm变化至10 mm，由图4可知，钳压长度不小于2mm时，干涉频谱的形状均比较规整，且钳压变形区段越长，频谱峰值越高，信号越强。

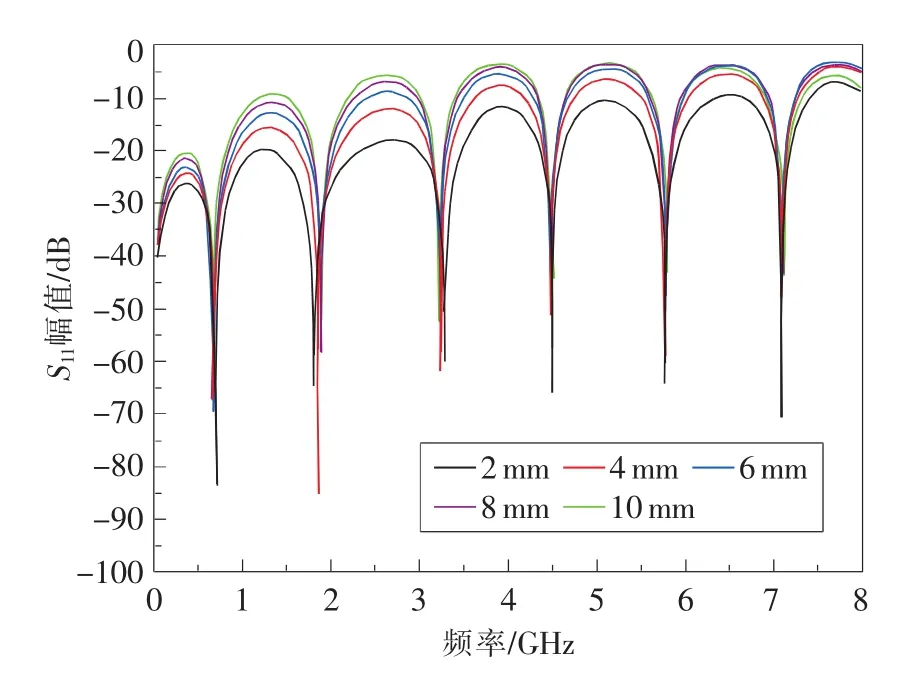
图4 钳压变形长度对干涉频谱的影响

3）钳压间距的影响

当反射点绝缘层外径为2mm，钳压变形长度为4 mm，钳压间距分别为 60，70，80 mm，由图 5可知，增大钳压间距，信号强度基本不受影响，只是频谱向左偏移，与式（3）的理论推导结果吻合。

4）反射点一致性的影响

图5 钳压间距对干涉频谱的影响

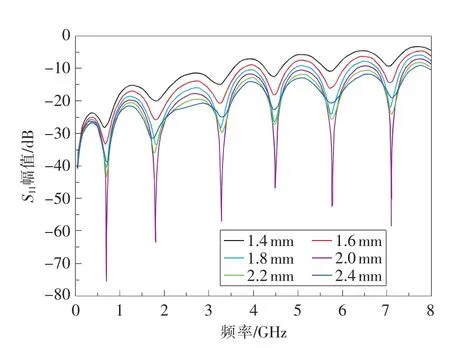
图6 反射点一致性对干涉频谱的影响

当钳压间距为80 mm，反射点钳压变形长度为2mm，第1个反射点的绝缘层外径R1为2mm，第2个反射点的绝缘层外径R2以0.2mm步距由1.4mm变化至2.4mm，仿真结果如图6所示。当R2由1.4mm向2mm变化时，信号峰值逐渐降低，干涉频谱的波峰和波谷也更加明显；当R2=R1=2 mm时，干涉现象最为明显；当R2超过2mm后，信号峰值继续降低，干涉频谱再次趋于平缓。由此可知，反射点一致性对信号质量有重要影响，制作传感器时应尽量保持两反射点的钳压变形程度一致，并需要对传感器的反射点进行封装保护，使两点的反射系数在测量过程中保持稳定。

2.2 CCFPI传感器的应变感知模拟

当同轴电缆受到拉伸，法珀腔长度（即反射点间距）改变使干涉谱发生频移。本文采用谱峰追迹法，追踪波谷频点的移动轨迹，求解电缆应变。

图7 CCFPI传感器的应变感知模拟

设置反射点绝缘层外径为2mm，钳压变形长度为 2 mm，钳压间距为 80 mm，并以 1 mm（12 500 με）的步距增大至88mm（100000με），相应的干涉频谱如图7（a）所示，干涉频谱的波谷随着两个反射点间距的增大向左移动，且谐振阶次越大，偏移越明显。选取第3～6个波谷记录频点，计算相比于未拉伸状态（即0 mm状态）的频移量，得到如图7（b）所示的应变频移曲线。由图可知，CCFPI传感器对应变成线性频移响应，且4条拟合直线的相关系数r2均超过0.998，线性度良好。

图8 液压钳挤压模块示意图

3 CCFPI传感器的试验研究

3.1 CCFPI传感器的制作方法

本文采用液压钳挤压软质金属套管（钳压法）制作CCFPI传感器。液压钳挤压模块示意图如图8所示，当左右两部分紧密贴合时，中部会余留已知孔径的开口，限制最大挤压程度，从而实现精准挤压。

根据上节仿真分析的结果可知，当反射点绝缘层外径在1.4～2mm范围内，干涉信号质量较好。假设挤压过程中，金属套管厚度（0.3 mm）和外导体厚度（0.3 mm）均保持不变，则挤压模块的孔径在2.6～3.2mm之间为宜，因而本试验选用孔径为3mm厚度为10mm的挤压模块制作CCFPI传感器。

将同轴电缆两端分别与矢量网络分析仪（vector network analyzer，VNA）和 50 Ω 负载相连，以 80 mm间距挤压12 mm长的金属套管带动电缆外导体变形，观察时域反射信号，发现两点的反射系数均在0.03左右，具有良好的一致性。为减轻反射点在试验拉伸中可能发生的不一致变形，用30 mm长的铜管灌注环氧树脂对其进行封装保护。同时，考虑到同轴电缆能够承受一定剪力或变形的优异结构特性，不对其他区段进行处理。反射点封装前后的实物图如图9所示。

3.2 CCFPI传感器的信号处理方法

将CCFPI传感器两端的接头分别与VNA和50Ω负载相连，直接测得频域的S11反射参数。采用联合时频技术解调，首先对S11反射谱进行线性调频Z逆变换（inverse chirp-Z transform，ICZT），得到 CCFPI传感器的时域信息；再借助VNA的时域门选通功能选取2个反射点（即时域信号上的2个反射峰）构成法珀腔；最后，通过chirp-Z变换（chirp-Z transform，CZT）将选通后的时域信号转换到频域，得到CCFPI的干涉频谱。具体变换流程如图10所示。

图9 封装前后反射点的实物图

3.3 试验过程及结果分析

为了观察CCFPI传感器对微小应变的反应，将CCFPI的标距设为800 mm，并通过光纤光栅（fiber bragg grating，FBG）和千分表读数了解电缆变形情况。设置VNA扫频范围为45MHz～8GHz，扫频点数为16001，试验用拉伸装置如图11所示。

忽略拉伸过程中同轴电缆绝缘层相对介电常数的改变，根据式（3），CCFPI传感器量测的应变值可以近似由计算，其中为当前拉伸步法珀腔的谐振频率，本试验选取第4个波谷进行解调。

图10 联合时频解调技术示意图

图11 拉伸试验装置图

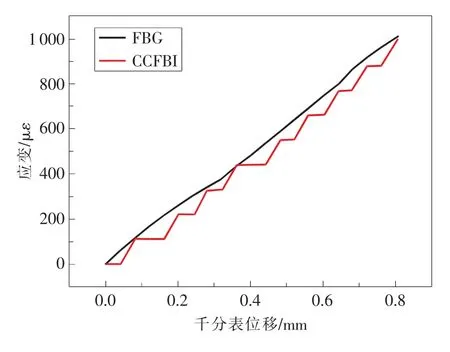
图12 小应变下CCFPI和FBG的测量结果

图13 大应变下CCFPI传感器的测量结果

将FBG粘贴在封装铜管的表面，以每级0.04mm（50 με）的步距拉伸电缆至千分表读数为0.8 mm（1000με），试验结果如图12所示，横轴表示千分表测量的位移值，纵轴表示CCFPI和FBG测量的应变值。由图，可以观察到CCFPI传感器的应变曲线存在水平段，实测应变值以110 με步距增长，说明在本文的试验条件下CCFPI传感器的分辨率可以达到110με，并且这一实测值，与利用仿真分析求得的波谷4的应变频移响应灵敏度3.83 kHz/με和扫频间距497.19kHz计算得出的分辨率[14]130με相符。同时，可以观察到CCFPI传感器的应变数值增长存在非等拉伸步数（2步或3步）增长的现象，原因有以下两点：1）拉伸过程中难以保证每个拉伸步长严格等于 0.04 mm（50 με）；2）两个精准拉伸步产生的变形仅为100 με，需要与相邻拉伸步的变形进行累积达到110με的分辨率，才能使CCFPI传感器产生干涉图谱频移的响应。另外，对比CCFPI和FBG的测量数据，可以发现二者吻合良好，说明CCFPI传感器可以感知小应变，且在小应变量程（1000με）范围内的测量结果真实可靠。

继续增大变形至3000με，之后以每级3000με的步距拉伸至CCFPI传感器失效（约140000με），用千分表读数换算的应变值作为横坐标，用CCFPI干涉图谱频移量换算的应变值作为纵坐标，可以得到如图13所示的测量结果。试验曲线具有良好的线性度，相关系数 r2为 0.99 867，斜率为 1.00 492，即CCFPI传感器的实测数据与千分表的测量结果高度吻合，表明CCFPI传感器具有大应变测量的能力，且测量结果真实可靠。

4 结束语

本文就钳压法制作工艺的不同结构参数对CCFPI传感信号的影响进行仿真模拟，分析得出：当反射点绝缘层外径在1.4～2mm范围内，钳压变形长度不小于2 mm，干涉信号质量较好；反射点间距基本只影响谐振频率，而反射点一致性则会严重影响信号质量。此外，模拟电缆拉伸过程观察到信号频移与电缆应变呈良好的线性关系。

依据模拟结果，优化CCFPI传感器的制作参数，并用环氧树脂对反射点进行封装保护，拉伸试验结果表明：CCFPI传感器的分辨率可以达到110με，并且测量结果在小应变量程（1 000 με）范围内与FBG吻合良好，说明CCFPI传感器的测量结果真实可靠。此外，测得CCFPI传感器的失效应变约为140000με，并且拉伸过程中始终与千分表读数吻合，说明CCFPI传感器可以实现大应变测量。

[1]欧进萍.重大工程结构智能传感网络与健康监测系统的研究与应用[J].中国科学基金，2005（1）：10-14.

[2]李宏男，高东伟，伊廷华.土木工程结构健康监测系统的研究状况与进展[J].力学进展，2008（2）：151-166.

[3]余成波，陶红艳.传感器与现代检测技术[M].2版.北京：清华大学出版社，2014：8-11.

[4]DOWDING C H， SU M B， O′CONNOR K.Measurement of rock mass deformation with grouted coaxial antenna cables[J].Rock Mechanics and Rock Engineering，1989，22（1）：1-23.

[5]MIAU B S.Fracture monitoring within concrete structure by time domain reflectometry[J].Engineering Fracture Mechanics，1990，35（1-3）：313-320.

[6]LIN M W，ABATAN A O，ZHANG W M.Crack damage detection of concrete structures using distributed electrical time domain reflectometry（ETDR） sensors[C]∥1999 Symposium on Smart Structures and Materials.International Society for Optics and Photonics，1999：297-304.

[7]KANG W F.Monitoring slope movement with time domain reflectometry[J].Geotechnical Field Instrumentation： Applications for Engineers and Geologists，2000.

[8]HUANG J.Coaxial cable Bragg grating[D].Rolla：Missouri University of Science and Technology，2012.

[9]李渊.同轴电缆布拉格电栅[D].大连：大连理工大学，2012.

[10]李鹏.同轴电缆布拉格电栅传感器原理及应用研究[D].大连：大连理工大学，2014.

[11]XIAO H， HUANG J， LAN X， et al.Distributed microwave Fabry-Perot interferometer device and method：U.S.Patent Application 14/341,944[P].2014-7-28.

[12]TRONTZ A， CHENG B， ZENG S， et al.Development of metal-ceramic coaxial cable Fabry-Pérot interferometric sensors for high temperature monitoring[J].Sensors，2015，15（10）：24914-24925.

[13]赵鹏.分布式同轴电缆裂纹传感器[D].大连：大连理工大学，2012.

[14]HUANG J，LAN X W，ZHU W G,et al.Interferogram reconstruction of cascaded coaxial cable fabry-perot interferometers for distributed sensing application[J].IEEE Sensors Journal，2016，16（11）：4495-4500.

（编辑：刘杨）

Coaxial cable Fabry-Perot sensor fabricated by clamping method

LIU Jia1，JIAO Tong1，ZHOU Zhi1，2， XIAO Hai3
（1.School of Civil Engineering，Dalian University of Technology，Dalian 116024，China；2.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China；3.Department of Electrical and Computer Engineering，Clemson University，Clemson 29630，USA）

To investigate the fabrication of CCFPI （coaxial cable Fabry-Perot interferometer） sensor with clamping method，the effects of different structural parameters on the sensing signal quality of CCFPI sensor is simulated.Simulation results show that the outer diameter of the insulation layer of CCFPI reflection point should be between 1.4 mm and 2 mm，the length of clamping deformation should not be less than 2mm and the consistency of reflection points has significant influence on the signal quality.In the simulation of the cable tensile process，the frequency shift of the interferogram responds to the cable strain linearly.On this basis，a CCFPI sensor is fabricated and a sensing performance test is carried out.The test results show that the strain measured by CCFPI sensor is consistent with that measured by the dial gauge in the whole tensile process with a fit slope of 1.00492 and correlation coefficient of 0.998 67.In addition，the value measured by CCFPI sensor is also consistent with that measured by the fiber bragg grating in small strain range，showing that the measured results of the sensor are accurate and reliable.It is also found the CCFPI sensor mentioned in this paper has a resolution of 110με and failure strain of about 140000με.

coaxial cable； Fabry-Perot sensor； clamping method； optimal design； large strain measurement

A

1674-5124（2017）09-0088-06

10.11857/j.issn.1674-5124.2017.09.016

2017-02-15；

2017-04-08

国家自然科学基金（61675038）

刘 嘉（1992-），女，辽宁法库县人，硕士研究生，专业方向为智能传感器与结构健康监测。