具有非线性发生率的多易感群体的传染病模型研究

商佩佩+袁朝晖

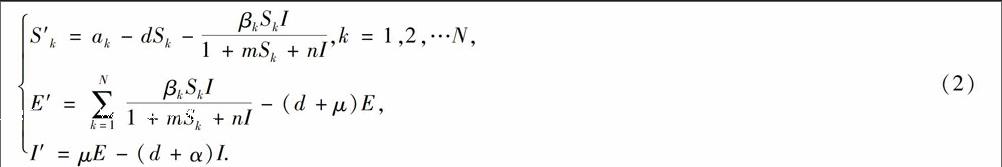
摘 要 本文主要研究一类具有Beddington-DeAngelis发生率的多易感群体的传染病模型.首先得到基本再生数R0，然后通过构造Lyapunov泛函和LaSalle不变原理得到了平衡点的全局渐近稳定条件.

关键词 非线性发生率；多易感种群；Lyapunov泛函；LaSalle不变原理；全局渐近稳定性

中图分类号 O175.14 文献标识码 A 文章编号 1000-2537（2017）05-0071-06

Study on Epidemic Models with Nonlinear Incidence Rate and Differential Susceptibility

SHANG Pei-pei*， YUAN Zhao-hui

（College of Mathematics and Econometrics， Hunan University， Changsha 410082， China）

Abstract This paper investigates a class of epidemic model with Beddington-DeAngelis incidence rate and differential susceptibility. The basic reproduction number R0 is first given， after which some sufficient conditions ensuring the stability of the system are obtained by constructing Lyapunov functional and using the LaSalle invariable principle.

Key words nonlinear incident rate； differential susceptibility； Lyapunov functional； LaSalle invariable principle； globally asymptotical stability

传染病历来就是危及人类健康的大敌，由于其传染性和流行性特征，一旦爆发很有可能大面积感染.在2014年西非的埃博拉疫情中，确诊死亡率高达88%.长期以来，人们运用多种方法研究传染病的发病机理和传播规律，以期控制和消除传染病[1].传染病动力学是通过建立数学模型，对传染病的流行规律进行定性、定量的研究[2，3]. 在经典的传染病模型中，大量使用的是双线性发生率和标准发生率[4，5].为了解释传染病传播过程中出现的一些复杂现象，近年来，又有一些能更好地模拟实际情况的非线性发生率被提出，如在文献[6]中，Capasso等提出了接触率可能依赖于患病者个体的饱和发生率βSI/（1+αI）和含有βSf（I）形式的非線性发生率. 文[7-9]分别针对一些特殊的具有非线性发生率的多种群传染病模型进行了讨论.

自然界中，受性别、年龄阶段、成长环境等多种因素的影响，不同易感群体由于自身免疫力及感染机会等存在差异，对传染病的易感程度并非完全相同，因此对多易感群体的传染病模型进行研究非常必要.

假设HIV易感者被HIV感染后存在一个潜伏期，处于潜伏期的感染者并不具有传染性，只有越过潜伏期的HIV感染者才具有传染性，并且由HIV感染者转化为艾滋病患者后，患者的活动能力由于受到了限制而无法传染HIV给易感者.基于此，本文将建立一个具有非线性发生率的多易感群体的特殊艾滋病传播模型模型，采用一种特殊的非线性发生率βkSkI1+mSk+nI（即Beddington-DeAngelis发生率[10]），并得到系统平衡点全局渐近稳定的条件.

1 模型与理论

1.1 模型的建立

符号说明及假设：

Sk，k=1，2，…，N. 易感者按其对HIV免疫力强弱、感染机会大小等的不同划分成N个不同的易感群体（注：对于处于潜伏期的患者E类和具有传染性的患者Ⅰ类不进行类别内分组）；

ak≥0： 第k类易感群体的输入率；

d≥0： 自然死亡率；

μ≥0： 从处于潜伏期的感染者变为具有传染性的患病者的转换系数；

α≥0： 处于患病早期的患者转化为患病晚期患者的转换系数；

γ≥0： 因病死亡系数；

βk≥0： 群体Sk中成员与早期患病者的有效接触率和易感程度.

其中，S，E，I，A分别表示HIV易感者、潜伏期中的HIV感染者、已具传染力的HIV感染者和艾滋病患者的数目.显然系统（1）的前面N+2个方程独立于最后的方程，因此下面仅考虑系统（1）的前N+2个方程构成的系统：

对于方程组（2），先假设初始条件为

其中，Sk（0）>0（k=1，2，…，N），E（0）>0，I（0）>0.

易知（2）存在唯一的正解.

1.2 解的有界性

注意到由（2）的前N个方程可以得到S′k≤ak-dSk，进而有

综上，Γ是系统（2）的正不变集.

1.3 平衡点和基本再生数

因此，h（I）在[0，+∞）上连续单调递增，于是得出F（I）是[0，+∞）上的连续单调减函数.注意到F（0）=R0-1，F（+∞）=-1，所以当R0>1时，F（I）必有唯一的正零点I*，然后将I*逐一代入方程组（5）的前N个方程和最后一个方程，可将S*k，E*分别用I*表示出来.以上部分证明出，当R0>1时，系统（2）存在唯一的地方病平衡点E*=（S*1，S*2，…，S*N，E*，I*）∈intΓ.endprint

1.4 穩定性

定理1 若R0≤1，则无病平衡点E0在Γ中是全局渐近稳定的.

证 令

仅当Sk=S*k，E=E*，I=I*（k=1，2，…，N）时，等号成立.

因此，对所有Sk，E，I>0（k=1，2，…，N），V′≤0成立，故地方病平衡点E*是稳定的.当且仅当Sk=S*k，E=E*，I=I*（k=1，2，…，N）时，V′=0，即Γ={（Sk，E，I）|V′=0，k=1，2，…，N}的最大紧不变集为单点集{E*}，则根据LaSalle不变原理，当R0>1时，地方病平衡点E*在IntΓ中是全局渐近稳定的.

2 数值仿真

这里将对系统（2）进行数值仿真，对系统内参数取值情况如下：

取k=3，a1=0.5，a2=0.48，a3=0.51，β1=d=m=n=μ=0.1，α=0.2，β2=0.12，β3=0.13，此时易算得R0=1.94>1. 取初值（S1（0），S2（0），S3（0），E（0），I（0））=（24.5，24.5，24.5，0.02，5）， 仿真结果见图1.

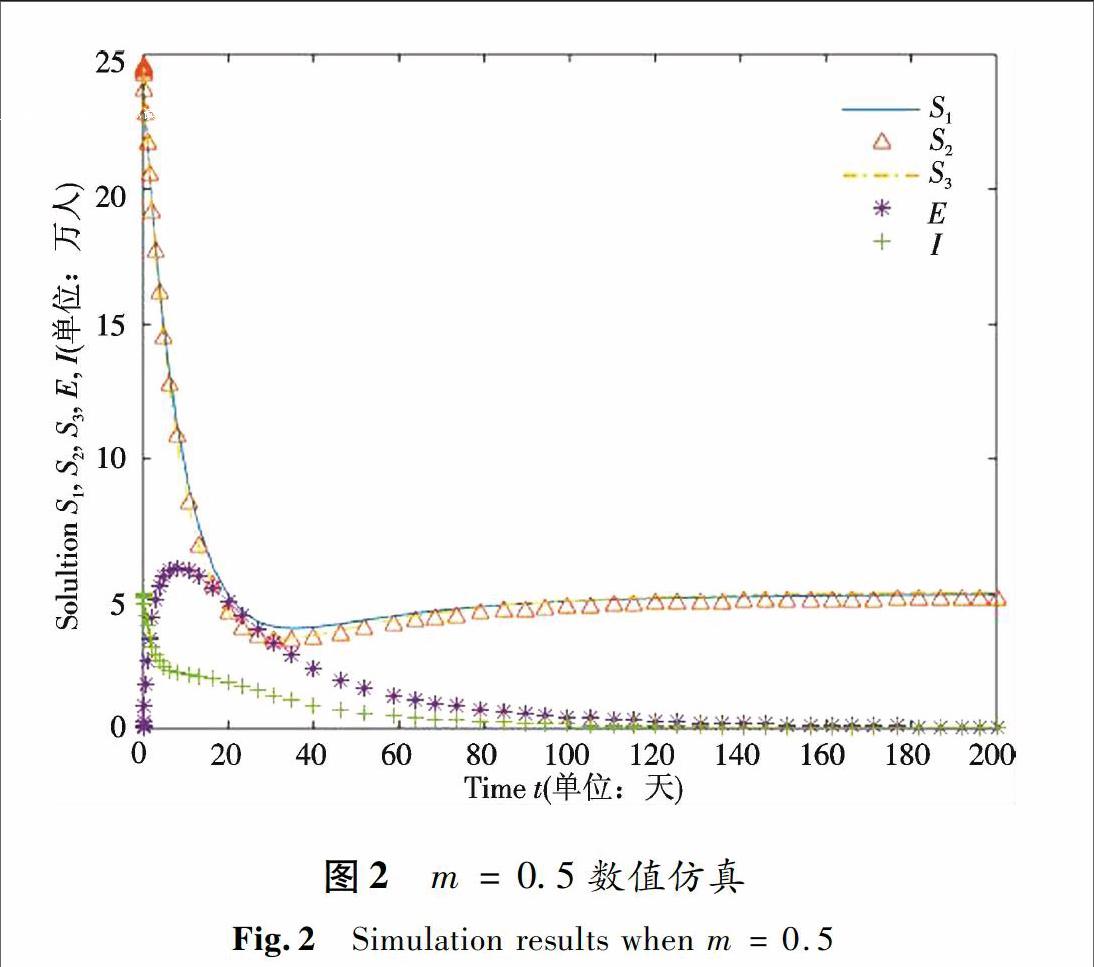
若保持其他参数和初值不变，取参数m=0.5， 此时R0=0.83<1. 仿真结果见图2.

由仿真结果可以看出， 当R0>1时， 系统是全局渐近稳定并一致持久的，说明疾病爆发后不会持续蔓延，系统在一定时间后会保持稳定；通过控制参数m使其变大，可以得到R0<1， 系统的无病平衡点是全局渐近稳定和一致持久的， 并且疾病在一段时间后会消亡.

参考文献：

[1] 马知恩，周义仓，王稳地.传染病动力学的数学建模与研究[M].北京：科学出版社，2004.

[2] 陆征一，周义仓.数学生物学进展[M].北京：科学出版社，2006.

[3] 张仲华.具一般非线性隔离函数和接触率的染病年龄SIRS模型平衡点的存在性及稳定[J].高校应用数学学报：A辑， 2011，26（1）：46-54.

[4] DRIESSCHE P， WANG L. Impact of group mixing on disease dynamics[J]. Math Biosci， 2010（228）：71-77.

[5] HETHCOTE H. Qualitative analyses of communicable disease models[J]. Math Biosci， 1976（7）：335-356.

[6] CAPASSO V，SERIO G.A Generalization of the kernmck-mckendrick deterministic epidemic model[J].Math Biosci， 1978（42）：41-61.

[7] YUAN Z H， WANG L. Global stability of epidemiological models with group mixing and nonlinear incidence rates [J]. Nonlinear Anal Real World Appl， 2010（11）：995-1004.

[8] YUAN Z H， ZOU X F. Global threshold property in an epidemic model for disease with latency spreading in a heterogeneous host population [J]. Nonlinear Anal Real World Appl， 2010（11）：3479-3490.

[9] KUNIYA T. Global stability analysis with a discretization approach for an age-structured multigroup SIR epidemic model [J]. Nonlinear Anal Real World Appl， 2011（12）： 2640-2655.

[10] HUANG G， MA W， TAKEUCHI Y. Global properties for virus dynamics model with Bedding-DeAngelis functional response[J]. Appl Math Lett， 2009（22）：1690-1693.

[11] LASALLE J. The Stability of Dynamics Systems[M]. Philadelphia： SIAM， 1976.endprint