第四次数学危机的数学基础和哲学根源①

王俊龙

(上海师范大学 期刊社，上海 200234)

第四次数学危机的数学基础和哲学根源①

王俊龙

(上海师范大学 期刊社，上海 200234)

文章分析第四次数学危机产生的数学基础和哲学根源。首先分析产生前三次数学危机的起因分别是发现不可公度量、引入无穷小量和出现最大集(所有集合的集合),从而把产生数学危机的原因归结为数概念及其运算模式。由于数学危机与人们对数和数学的不完善的甚至错误的认知有关,因此,即使人们以为消除了危机,但是潜在的数学危机依然存在。因此,第二次和第三次数学危机蕴含了第四次数学危机。论证的关键是,在实数连续统R上发现非连续量——离散数,通过引进连续区间变量(含离散数)(x,y)=[y]-[x],在连续区间(0,I)上建立了扩展的布尔代数；进而,在连续区间(-0,0)上成功地建立了太极代数和广义太极代数。这里0和-0分别表示绝对全集和绝对空集,预示着所有实数介于0和-0之间。而现有数学理论不能解释实数连续统R上的非连续量——离散数,从而揭示了现代数学存在第四次危机的原因,并显示人们对自然数集N和实数集R的描述或认知的根深蒂固的局限性。还将在中国先秦哲学经典中寻找产生第四次数学危机的哲学根源。

数学危机;自然数;实数连续统;极数;非连续量;布尔代数;广义太极代数

因为发现不可公度量、无穷小量、最大集(所有集合的集合)，分别引发了数学史上的三次数学危机。存在第四次数学危机是基于数学和哲学两方面原因:数学上发现非连续量——离散数,哲学上的非实在论——空无观，以及基于数学和哲学两方面的共同因素——极数的存在:0是极数之一,-0是另一极数。

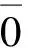
一 三次数学危机:数概念及其运算

人类数学史曾发生三次数学危机。是什么导致的数学危机?考察发现,数概念及其运算模式导致了数学危机。什么是数?当人们对此形成一个普遍而固定的认知模式时,一旦发现不满足这一既定模式的新数,数学危机就产生了。

先看第一次数学危机。

如果认为数就是整数或整数之比,那么,当发现有一种量不能表为两个整数之比时就将导致数学危机。第一次数学危机就是这样产生的。

第一次数学危机是由数概念及其运算这两个因素存在的局限性而导致的。对于数而言,并不限于整数或有理分数。整数可视为分母为1的有理分数。整数或整数之比都可表为有理分数。

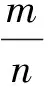
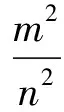
因此,m2=2n2是偶数,从而m必是偶数,推知n是奇数。

设m=2p,则4p2=2n2,即n2=2p2,从而n是偶数。

这样就导致矛盾。*在欧几里得《几何原本》第十篇中见此证明。

所以,一个边长为1的正方形,其对角线长度不可能是任何一个有理分数。

有理分数表现整数的可通约性,不可通约性的发现引起第一次数学危机。[1]7

几何中发现的不可通约性的量属非有理分数,被称之为无理数。当接受不可公度量的存在时,人们对数的认知水平第一次通过几何学得到大幅度提高。其进步成果的标志就是古希腊的《几何原本》,其作者是公元3世纪的欧几里得。

再看第二次数学危机。

第二次数学危机的发生与微积分中无穷小量及其运算有关,微积分是由牛顿(1642-1727)和莱布尼兹(1646-1716)发现并引入数学分析中的。

虽然18世纪的数学家成功地用微积分解决了许多实际问题,但是,当时的数学思想是不严密的、直观的,强调形式的计算而不管基础是否可靠。对于无穷小、无穷大、连续性、微分符号的使用条件等都是不清楚的。一直到19世纪20年代，一些数学家才比较关注于微积分的严格基础,从波尔查诺、阿贝尔、柯西、狄里赫利等人的工作开始,一直到威尔斯特拉斯、戴德金和康托进一步加以完善，才基本上解决了矛盾,为数学分析奠定了一个相对严格的基础。[1]17

最后看第三次数学危机。

康托创立的集合论是现代数学的基础,也是产生危机的来源。集合论的产生与数的集合元素的可数性和不可数性密切相关。1873年11月,康托在与戴德金的通信中认为有理数的集合其元素是“可数的”,即与自然数的集合可形成一一对应的关系。但是他不知道对于实数集合这种一一对应的关系是否能做到。同年12月,康托又写信给戴德金,已能证明全体实数是“不可数的”,即与自然数不能形成一一对应的关系。集合论就这样产生了,为数学开辟了一个新的方向。

但是,康托的朴素集合论中存在悖论。1899年7月28日,在给戴德金的信中,康托指出,不能谈论由一切集合构成的集合,否则会陷入矛盾。

一个集合Y的基数,用|Y|表示。康托证明,如果P(Y)是Y的所有子集构成的集合,即Y的幂集,则|Y|lt;|P(Y)|。设C是所有集合的集合,因此,P(C)也是C的子集,所以|P(C)|lt;|C|;但是,由康托定理,|C|lt;|P(C)|,这就导致矛盾。[1]86-87

这实际上就是罗素悖论的内容。1908年策梅罗采用集合公理化的方法来消除罗素悖论。策梅罗在《关于集合论基础的研究Ⅰ》中指出:“这个问题必须这样地解决。使得这些原理足够地狭窄,足以排除掉所有的矛盾。同时,又要足够地宽广,能够保留这个理论所有有价值的东西。”[1]98

几乎可以这样说,上述三次数学危机都是由数及其运算模式导致的。第一次是发现不可公度量导致有理数数学理论产生危机,第二次是无穷小量的引入及其运算引发的微积分数学基础的危机,第三次是集合悖论的出现(实际上是最大集合的发现)导致集合论的危机。

二 现代数学的基础:自然数集N和实数集R

第一次数学危机出现前只有自然数和建立在自然数基础上的有理数,引进不可公度量之后,第一次数学危机消除了。人们不仅认识到自然数也认识了实数,同时为现代数学提供了自然数集N和实数集R。

皮亚诺公理是自然数公理化的反映,皮亚诺肯定的五个基本命题是:

(1)0是一个数。

(2)任何数的后继是一个数。

(3)没有两个数有相同的后继。

(4)0不是任何数的后继。

(5)任何性质,如果0有此性质，又如果任一数有此性质,它的后继必定也有此性质，那么所有的数都有此性质。

五个基本命题中的最后一个是数学归纳法原则。[2]11

康托的连续统是对实数的连续性的假设。“由于任何连续域,无论其维数如何,都可以认为它与一个线性连续点集等势,因此连续性研究可以归结为对实数连续统R的研究。”[3]42

“康托挑选了两种特殊情形:可数集——它们的势是自然数集N的势;连续统或不可数集——它们的势是实数集R的势。”[3]49

表面上看,现代数学建立在集合论基础之上。实质上,现有数学建立在自然数和实数基础上。自然数是离散的,其中只有最小数而没有最大数;实数是连续的,其中既有可数数也有不可数数。从只有最小而没有最大看,现有集合论中只有最小集而没有最大集,现有集合论是自然数的一种反映；从既有可数也有不可数看,现有集合论中既有可数集也有不可数集,现有集合论是实数的一种反映。

三 为什么第四次数学危机不可避免?

任何一次数学危机都经历四个阶段:潜在危机、危机显现、感知危害和危机消除。

任何一次数学危机在人们发现前就已经隐蔽地存于人们的认知世界中了,因为人们对数和数学的认知总是不完善的,甚至是错误的,所以,人们对数和数学形成的每一个明确的认知就隐藏着危机。随着人们对数和数学认知范围的扩大和认知水平的提高,原本潜藏着的危机逐步显现出来。一旦当人们意识到错误的认知影响到整个数学基础时,数学危机就爆发了,消除危机变得刻不容缓。

由于数学危机与人们对数和数学的不完善的甚至错误的认知有关,因此,即使人们以为消除了危机，数学危机依然存在。

前述第二次和第三次数学危机蕴含了第四次数学危机,这是由于三次数学危机的消除只有第一次是相对彻底的,且是开放的。相对彻底是因为引进不可公度量,从而消除了危机。引进新数是一种开放机制,随后人们又引进了复数、代数数和超越数等新数。而第二次数学危机是由无穷小量(其极限是最小量)引发的,第三次数学危机是由最大集(对应最大元)引发的。第二次数学危机并没有真正解决最小量问题:0果真是无穷小量的极限吗?第三次数学危机并没有真正解决最大集问题:果真不能存在最大集吗?由于第二次和第三次数学危机消除得并不彻底或不是根本性解决方案,必然引发第四次数学危机。

对于数而言,最小数和最大数都是存在的,而现有数学的实数系中既没有最小数也没有最大数。同样,对于集合而言,最小集和最大集都是存在的,而现有集合论中只存在最小集(即空集)而不允许存在最大集。因此,一旦出现最小数和最大数都允许存在的数学新结构，就会引发第四次数学危机。

具体说来,现有数学关于自然数N和实数连续统R存在一系列错误认知。

关于自然数N的错误认知主要有:

(1)以为自然数是无限多的,只有最小数而没有最大数。

(2)以为-0=0,或以为-0没有独立存在的意义。

(3)以为0作为坐标系的原点是完全合理的。

(4)以为-n是与n相抵消的数,或以为0是空集。

关于实数连续统R的错误认知主要有:

(1)只承认潜无限而不承认存在实无限。或者,虽然承认实无限,但认为存在无穷上升的超穷基数。[3]110

(2)以为任意x和y,xlt;y,xgt;y,x=y,三种可能中有且仅有一种成立。[3]98，[4]116

(3)以为实数连续统R中只有连续量,且不存在包含所有实数的最大数。[1]86-87

(4)以为0是-n和n之间的中间数。

上述关于自然数N和实数连续统R的一系列错误认知严重阻碍数学的进一步发展,由此可以认为,现代数学依然存在严重危机。这是数学史上面临的第四次数学危机,也是最深刻、最全面的一次危机。

四 扩展的布尔代数:连续区间(0,I)上的逻辑代数

皮亚诺公理是对自然数形象的公理化刻画,其中第一条“0是一个数”和第四条“0不是任何数的后继”是表示0是最小的自然数吗?“0是一个数”和“0不是任何数的后继”不也可以表示0是最大的自然数吗?

现在有一种把0引进自然数构成“扩展的自然数”的做法就是把0看成是最小的自然数,0果真是最小自然数吗?

在布尔代数中,则把1作为全集,把0作为空集。在用可数集构造后继集并与自然数对应时,则把空集等于0。0果真是空集吗?

或是受布尔代数影响,康托视0至1的闭区间(0,1)为连续统。“完备集S和连续统(0,1)有相同的势,从而所有线性完备集都有相同的势……对任何n维空间的完备集也有同样的结果。”[3]96

布尔视0为空集、视1为全集，与算术运算规则中0是加法单位元、1是乘法单位元有关。在算术运算中,a+0=a,a×1=a。

其实,布尔加不同于算术加,布尔乘也不同于算术乘。

考察连续区间(0,I)上的逻辑代数将有助于认清算术运算和逻辑运算之间的差异,也有助于认清数的本质。这里I是任意I≥1的自然数。

连续区间(0,I)上的逻辑代数,实际上是连续区间(0,1)上的布尔代数的扩展。*扩展的布尔代数,参见王俊龙:《论语言研究需要怎样的逻辑工具》,《山西大学学报》2013年第5期,第57-61页。

定义设(x,y)是(0,I)上的任一连续区间,这里0≤x≤y≤I。

定义设[x]=(0,x),[y]=(0,y),则(x,y)=[y]-[x]。

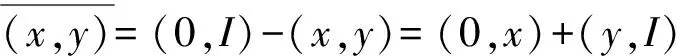
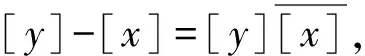
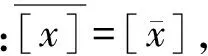
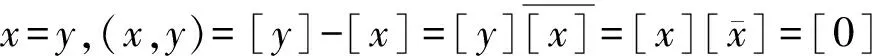
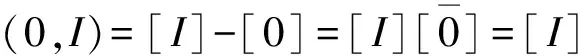
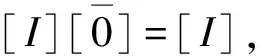
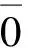
下面将建构的连续区间(-0,0)上的逻辑代数,将以-0或[-0]为绝对空集，以0或[0]为绝对全集,同时将证明:-0≠0。众所周知,在算术运算中-0=0。因此,理解并接受连续区间(-0,0)上的逻辑代数，需要对现有数学基础及其观念重新加以审视。

五 广义太极代数:连续区间(-0,0)上的逻辑代数

太极代数[5]和广义太极代数[6]是连续区间(-0,0)上的逻辑代数,这里以-0或[-0]为绝对空集,以0或[0]为绝对全集。

定义设(x,y)是(-0,0)上的任一连续区间,这里-0≤x≤y≤0。

定义设[x]=(-0,x),[y]=(-0,y),则(x,y)=[y]-[x]。

定义(x,y)的补集为-(x,y)=(-0,0)-(x,y)=(-0,x)+(y,0)

规定:若[x]=[y],则x=y;规定:-[x]=[-x],且称-x是x的绝对补数。

若设[y]-[x]=[y][-x],则-(x,y)=-([y][-x])=[x]+[-y]。

易知,-(-0,y)=-([y][-(-0)])=[-0]+[-y]=[-y]=(y,0)。

若(x,y)=[y]-[x],且[y]-[x]=[y][-x],则(x,y)=[y][-x]。易得

-(x,y)=-([-x][y])=[x]+[-y]

-(-(x,y))=-([x]+[-y])=[-x][y]

满足De Morgan律。

[x]+[-x]=[0]

[x][-x]=[-0]

-([x]+[-x])=[x][-x]

-([x][-x])=[x]+[-x]

满足De Morgan律。

逻辑公式[x]+[-x]=[0]与算术运算公式x+(-x)=0极相似,但是,前者的[0]与后者的0其含义是极为不同的。算术运算中x-x=x+(-x)=0,0的含义是空集。逻辑运算中-([x]-[x])=[x]+[-x]=-[-0]=[0],其中[-0]是空集,[0]是全集。

当x=y,(x,y)=[y]-[x]=[y][-x]=[x][-x]=[-0]是绝对空集、最小集。说明连续统(-0,0)上的任一点是空集。

因为-(-[x])=[x],所以,(-0,0)=[0]-[-0]=[0][-(-0)]=[0]是绝对全集、最大集。说明连续区间(-0,0)是所有连续区间(x,y)的集合(含所有非连续量)。换言之,连续区间(-0,0)是所有连续区间(x,y)的连续区间。

六 结论

通过上述连续区间上的逻辑代数的建构大致可以得出以下一些结论:

(1)布尔代数是连续区间(0,1)上的逻辑代数,扩展的布尔代数是连续区间(0,I)上的逻辑代数,二者都是以0点为最小集或空集。布尔设定前者以1为最大集或相对全集,设定后者任意I≥1的自然数为最大集或相对全集。

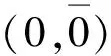
(4)太极代数和广义太极代数是连续区间(-0,0)上的逻辑代数,这里以-0或[-0]为绝对空集,以0或[0]为绝对全集。

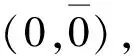
(7) 存在非连续量。连续区间变量(x,y)=[y]-[x]是逻辑变量(含非连续量),或者说,也包含新的数——离散数。

上述结论说明,现有数学关于自然数N和实数连续统R存在一系列错误认知,需要确立以下新的认知。

关于自然数N需要确立的新认知:

(1)自然数是无限多的,既有最小数也有最大数。

(2)-0=0,只是算术运算的结果。在逻辑运算中,-0具有独立存在的意义且-0≠0。

(3)0作为坐标系的原点,在-0=0的前提下是合理的。但是,在-0≠0的前提下,0作为坐标系的原点是不合理的。

(4)-n是与n相抵消的数,或以为0是空集,只是算术运算的结果。在逻辑运算中,[-n]与[n]是一对互补数,[-n]表示所有除[n]以外的数。

关于实数连续统R需要确立的新认知:

(1)存在实无限,存在上升的超穷基数,但是存在最大基数。

(2)对于任意x和y,xlt;y,xgt;y,x=y,三种可能中有且仅有一种成立。这是算术运算规则下连续量遵循的三分律[4]116。逻辑运算规则下,三分律对于非连续量不能成立。[7]

(3)实数连续统R包含连续量和非连续量,且存在包含所有实数的最大数。[6]

(4)0是-n和n之间的中间数,在-0=0的前提下可以成立。但是,在-0≠0的前提下,0是极数之一,-0是另一极数。

七 空无观:连续区间(-0,0)的哲学根源

惠施曰:“至大无外,谓之大一。至小无内,谓之小一。”大一是最大元,小一是最小元。

《老子》曰:“天下万物生于有,有生于无。”王弼注曰:“欲将全有必返于无也。”无,不是真没有,而是全有。

最小元,谓之空;最大元,谓之无。一切存在介于空和无之间。

定义无,一无所现。空,一无所有。

连续区间(-0,0)中涉及两个无量:0和-0。其中0义为无,-0义为空。或者说,0是无在数学上的反映,-0是空在数学上的反映。

哲学上,一切存在介于空和无之间。数学上,所有实数介于-0和0之间。

这样,我们就从哲学上的空和无两极找到了数学上相对应的实数的两个极限:-0和0。前者是最小数,后者是最大数。

空和无是绝对的存在,其存在不以任何实有为前提。虽然无中生有,但是,生而不有。

同样,-0和0是绝对存在,其存在不以任何实数为前提。-0和0二元即可构建本原逻辑代数系统。

[0]+[-0]=[0]

[0][-0]=[-0]

[-0]为绝对空集,是真正的逻辑加法单位元。[0]为绝对全集,是真正的逻辑乘法单位元。布尔代数中的0是套用算术加法单位元,是伪逻辑加法单位元;布尔代数中的1是套用算术乘法单位元,是伪逻辑乘法单位元。[6]

世界上的一切是无中生有的。同样,数学上的所有数也是无中生有的。

连续区间(-0,0)就是实数连续统R。 对于任意一对互补数x和-x,则有

[x]+[-x]=[0]

[x][-x]=[-0]

这两个公式表明,任意一对互补数x和-x都受到-0和0的约束。0最大,是所有互补数的共和,-0最小,是所有互补数的连接。

x和-x,表示有。有(存在)是分阴分阳的。《说卦》曰:“分阴分阳,叠用柔刚。”《系辞》曰:“一阴一阳之谓道。”

阴、阳、空、无是四个最基本的元素。阴阳相反而互补,空无相反而互补。

若用-0和0分别表示空和无,用-1和1分别表示阴爻和阳爻,则得太极代数[5]，[8]234-236:

[1]+[-1]=[0]

[1][-1]=[-0]

太极代数是定义在集合{-0,0,-1,1}上的四元逻辑代数,有一套严格的运算规则。[8]245，246

这样一来,从惠施“大一”(最大存在)和“小一”(最小存在)开始,进而认识到空(一无所有)和无(一无所现)。空(对应小一)和无(对应大一)是一对绝对矛盾,也是一对最高范畴。再到“一阴一阳之谓道”的二分世界观。最后,得到太极代数,为连续区间(-0,0)上建立的逻辑代数找到了哲学根源——空无观。

[1]胡作玄.第三次数学危机[M].成都:四川人民出版社,1985.

[2]〔英〕罗 素.数理哲学导论[M].曼成书，译.北京:商务印书馆,1982.

[3]〔美〕周·道本.康托的无穷的数学和哲学[M].郑毓信，刘晓力，编译.大连：大连理工大学出版社，2008.

[4]〔美〕Enderton Herbert B.数理逻辑[M].第2版.沈复兴等,译.北京：人民邮电出版社，2007.

[5]王俊龙.论太极代数及其辩证内涵[J].湖南师范大学社会科学学报,2009(3)：43-47.

[6]王俊龙.广义太极代数：R上的逻辑代数[J].湖南师范大学自然科学学报，2014(5)：85-89.

[7]王俊龙.太极数理哲学:身心统一的世界观[J].学术月刊,2013(6)：27-35.

[8]王俊龙.《周易》经传数理研究[M].北京:人民出版社,2015.

(责任编辑 郭庆华)

TheMathematicalBasisandPhilosophicalRootsoftheFourthMathematicalCrisis

WANG Jun-long

(AcademicJournalOffice,ShanghaiNormalUniversity,Shanghai200234，China)

This paper analyzes the mathematical basis and philosophical roots of the fourth mathematical crisis. First of all, the causes of the first three mathematical crisis are the discovery of unqualified measures, the introduction of infinitesimals and the emergence of the largest set, so that the cause of the mathematical crisis is attributed to the number of concepts and their computing mode. Because the mathematical crisis is related to the imperfect or erroneous perception of numbers and mathematics, even if people think that the crisis is eliminated, the underlying mathematical crisis still exists. Thus, the second and third mathematical crisis contained the fourth mathematical crisis. The key to the argument is that the discontinuous quantity - discrete number is found on the real continuous R, and the extended Boolean algebra is established on the continuous interval (0,I) by introducing the continuous interval variable (including the discrete number) (x,y)=[y]-[x].Furthermore, the Tai Chi algebra and the generalized Tai Chi algebra are successfully established on the continuous interval (-0,0), where 0 and -0 denote the absolute and absolute vacancies, respectively, which indicates that all real numbers are between 0 and -0. The existing mathematical theory is difficult to explain the discontinuous quantity - discrete number on the real continuous R, which reveals the reason of the fourth crisis of modern mathematics and shows the description or cognition of the natural number set N and the real number set R deep-rooted limitations. And will find the philosophical roots of the fourth mathematical danger in the Chinese pre-Qin philosophical classics.

mathematical crisis;natural number;real number continuum; polar number; discontinuous quantity; Boolean algebra; generalized Tai Chi algebra

2017-04-16

王俊龙(1959-)，男，江苏盐城人，博士，上海师范大学期刊社副研究员，上海师范大学知识与价值科学研究所特聘研究员，主要从事《周易》数理研究。

① 本文为2017年全国数学哲学学术研讨会参会论文(2017年4月16-17日,山西太原),这里发表时删减了一些数学公式。

10.13451/j.cnki.shanxi.univ(phil.soc.).2017.06.001

B221

A

1000-5935(2017)06-0001-06