疏浚泥浆浓度最优控制跟踪器的设计与实现

朱文亮 ，倪福生 ，王素红 ，尹 飞

1.河海大学 港口海岸与近海工程学院，南京 210098 2.河海大学 疏浚技术教育部工程研究中心，江苏 常州 213022 3.连云港市水利局，江苏 连云港 222006

疏浚泥浆浓度最优控制跟踪器的设计与实现

朱文亮1，2，倪福生1，2，王素红3，尹 飞3

1.河海大学 港口海岸与近海工程学院，南京 210098 2.河海大学 疏浚技术教育部工程研究中心，江苏 常州 213022 3.连云港市水利局，江苏 连云港 222006

在疏浚作业过程中，绞吸挖泥船主要的作业参数是由操作人员根据自己的经验确定的，而疏浚操作人员的经验和理论水平也相差较大，所以手动作业的实际产量要远远低于预计产量，效率低下，作业成本偏高，作业质量较差。为了克服该缺点，提出一种基于BP（Back-Propagation）神经网络的疏浚横移过程状态空间建模方法，并设计了疏浚横移过程线性二次型泥浆浓度最优控制跟踪器，应用于疏浚作业智能化控制中。仿真结果表明：二次型最优控制跟踪器的控制稳定性好、响应快、滞后小，跟踪效果好，泥浆浓度提高显著，较好地克服了人工操作缺点。

挖泥船；疏浚系统；状态空间；模型；二次型；最优控制；策略

1 引言

绞吸式挖泥船作为一种常用的水力式挖泥船，其工作的基本原理是依靠绞刀装置对土层进行切削并与附近的水混合形成泥浆，再通过泥泵将泥浆吸入并输送到指定抛泥区。如图1所示，绞吸挖泥船主要由船体、定位桩系统、泥浆输送系统（包括柴油机、泥泵、吸排泥管和相关仪表）、绞刀切削系统、台车移位系统、横移系统、作业综合控制系统等构成。挖泥船的作业过程一般如下[1]：当挖泥船到达施工地点后首先对船体进行定位，将主定位桩插入河底，并利用抛锚杆将横移锚抛至船体两边，以定位整个船体。然后启动桥架绞车将桥架缓慢下放至水中，绞刀和泥泵开始工作，桥架下放至适当位置后，横移绞车在锚和主定位桩的配合下，通过缆索使绞刀与船体一起以主定位桩为中心转动，实现扇形挖泥作业。绞刀以一定速度转动，同时左右横移，接触到的泥层被切削下来与水混合形成泥浆，泥泵工作形成真空，在负压的作用下，泥浆吸入管道并输送到指定场所。当绞刀切削完了一个断面的所有泥层后，通过台车液压缸使船体前进一个步长，继续开挖下一断面。

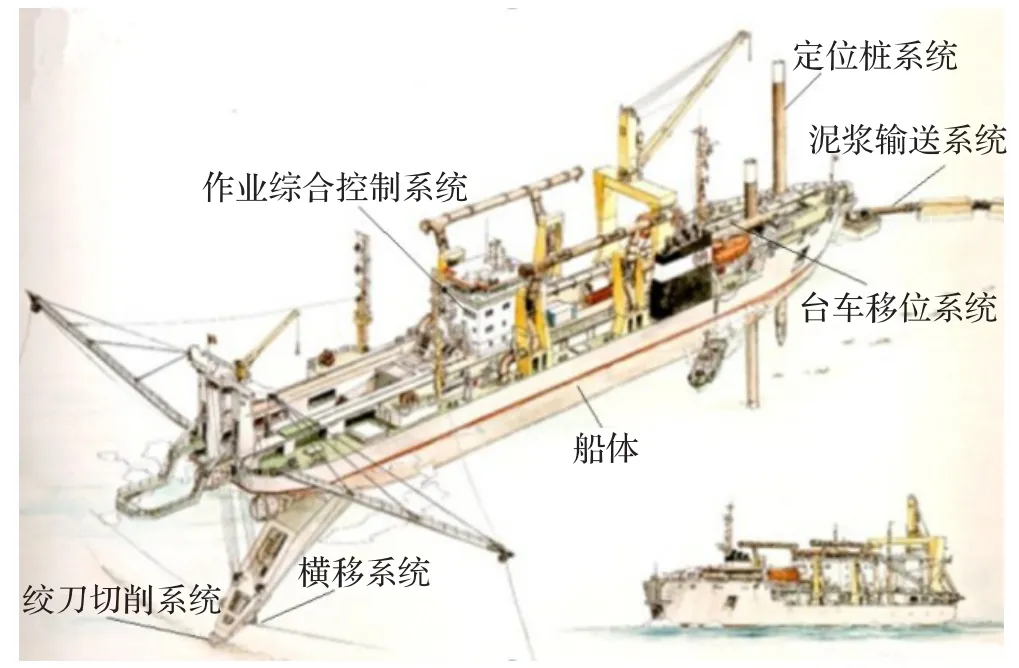
图1 绞吸挖泥船系统组成图

智能控制技术是解决疏浚作业自动化与系统集成控制最有力的工具。疏浚作业过程具有高度的复杂性和不确定性，应用传统的控制方法基本不太可能实现对疏浚作业有效的控制。目前，在实际的疏浚过程中施工作业人员还主要是在对疏浚作业过程数据观察的基础上，结合自己以往积累的施工经验和对疏浚作业过程的理解来给出调整方法。这些经验性的总结一般是定性、模糊的，并不能准确地用数据和公式表达且随意性较大，疏浚作业过程中挖泥船主要的作业参数是由操作人员根据自己的经验、试挖情况以及挖泥船实际作业效果灵活确定的，所以手动作业的实际产量要远远低于预计产量，效率低下，作业成本偏高，作业质量较差。如何建立疏浚系统的状态空间数学模型和设计疏浚系统优化控制方案，就是摆在疏浚研究人员的一项重大的课题。在国外，疏浚作业控制系统优化和自动控制研究开始于20世纪90年代，许多机构做了大量的研究工作[2-4]。而国内，相关的研究工作也已开展了近十年，唐建中[5]提出了疏浚作业系统控制结构，采用自校正前馈补偿控制方案分别实现了泥浆浓度和流动速度这两个相互耦合的系统的控制。闭治跃[6]提出一种挖泥船管道泥浆浓度输送系统效率优化评价方法，并对泥浆管道输送系统的过程控制、工况点在线动态优化方法和多泵协调控制策略进行了相关研究。倪福生等[7-14]对泥沙输送、系统动态特性进行了大量的研究，应用贝叶斯正则化法，对绞吸挖泥船现场实测数据进行分析计算，分别研究了绞刀横移速度、管道流速、绞刀步进、绞刀工作压力等因素对产量的影响。

绞吸挖泥船疏浚系统是一个复杂的多输入多输出系统，系统控制优化的实质表现为在相互冲突的多个目标之间寻求平衡和总体目标的最大化。作业综合控制系统架构如图2所示，主要分三个层次，决策控制层、过程控制层和目标控制层，决策控制层可以根据自身实时监测数据，采用多种优化策略来做出智能决策，决策量用于过程控制中，通过过程控制实现对控制目标的调节。疏浚作业的决策层要想实现最优的控制目标，就需要建立疏浚作业空间在相邻时刻的状态转移变化规律，即状态空间模型，在此模型的基础上才能根据具体施工需求设计相应的控制策略。

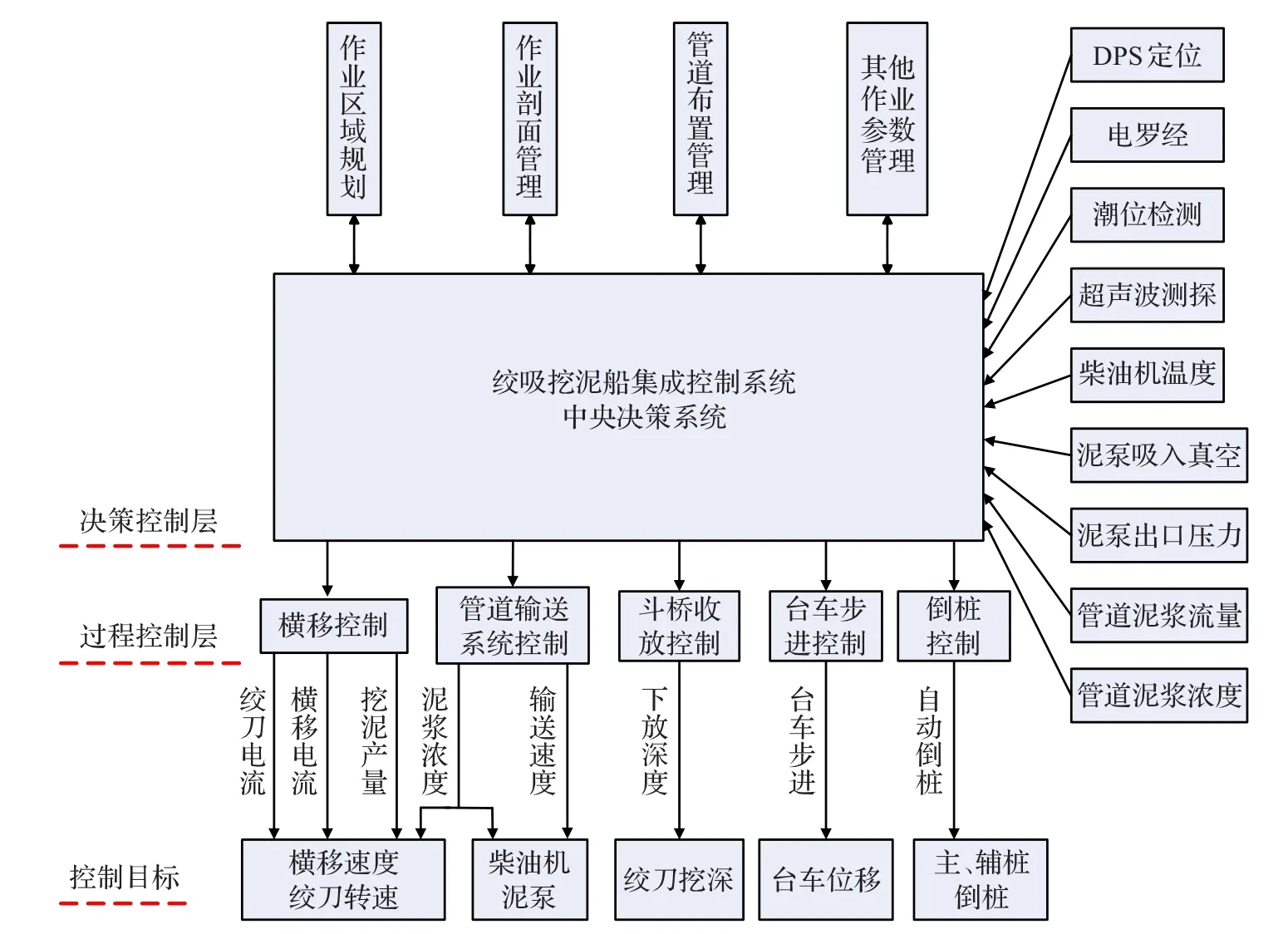
图2 作业综合控制系统架构图

构建疏浚系统状态空间模型问题实质上是系统辨识的问题，在系统的结构已知，参数未知的情况下，系统辨识问题就简化为参数估计的问题。对于参数估计问题的研究，因为在大多数情况下不能直接应用极大似然估计方法，状态空间模型的参数估计比一般的时间序列模型要困难得多，从而需要对状态空间模型的不同子类采用不同的估计策略[15]。比如，Zoubin Ghahramani等[16]利用EM算法对线性动态系统进行参数估计。Schon T等[17]讨论了状态或参数是线性的状态空间模型的参数估计问题，Doucet A等[18]使用粒子滤波实现模型的参数估计。Gibson S等[19]讨论了双线性系统的极大似然参数估计。标准BP网络的逆向传播算法具有思路清晰、结构严谨、可操作性强等特点，而且一个三层的BP网络可以完成任意的n维到m维的映射，被较为广泛地应用于参数估计和预测，熊建华[20]将BP神经网络和降维法相结合，对GRM下的项目参数和考生能力参数进行估计。阮士平等[21]使用LM-BP算法作了综合水质评价研究，LM-BP算法是梯度下降法与高斯牛顿法的结合，既有高斯-牛顿算法的快速收敛特性又有梯度下降法的全局特性，此算法收敛速度最快、鲁棒性好，可以有效地改善网络收敛性能，而且速度很快[22]。参数估计有离线估计与在线估计两种方法，离线估计是把一定时间内积累的采集数据进行一次性的估计计算，在线估计是在每个采集周期都根据新的采集数据进行一次递推估计计算，节省计算时间和内存空间，便于及时掌握系统现状。文中提出一种基于BP神经网络的疏浚横移过程状态空间建模方法，建立了描述挖泥船疏浚过程各状态变量在相邻时刻状态转移变化规律的状态空间模型；在此模型基础上，设计了绞吸挖泥船横移过程线性二次型泥浆浓度最优控制跟踪器，应用于疏浚作业智能化控制中。在MATLAB仿真平台上进行仿真分析，对应用效果与挖泥船施工实时数据进行比较；结果表明：线性二次型最优控制跟踪器控制稳定性好、响应快、滞后小，跟踪效果好，泥浆浓度提高显著，较好地克服了人工操作缺点。

2 疏浚系统建模方法

2.1 疏浚系统建模问题的描述

现代控制理论的核心思想有三点：（1）引入状态变量概念；（2）建立描述状态变化的模型即状态方程；（3）给出了传递状态信息的输出方程。状态方程是描述相邻时刻的状态转移变化规律，输出方程描述观测信息和状态之间的联系。可近似地把挖泥船疏浚系统状态空间看作离散线性定常系统，其状态空间表达式表示如下：

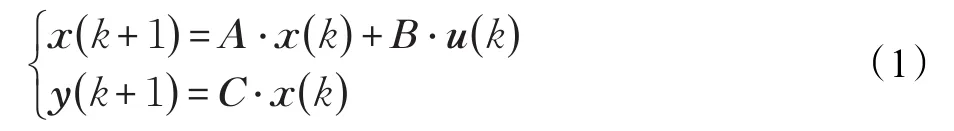
式中，x()

t为n维状态向量，在疏浚作业状态空间中，可以选择管道流速、泥浆浓度、绞刀功率、泥泵真空度、绞刀横移速度、绞刀步进量等作为状态变量，其初始状态为x(t0)；u(t)为m维控制向量；y(t)为l维输出向量；A、B、C分别为n×n维、n×m维和l×n维的状态阵、控制阵和输出阵。所构建的疏浚作业状态空间模型为m输入l输出定常系统，通过该状态空间表达式就可以准确地描述疏浚作业过程的动态变化特性。把状态方程写为如下方程组形式：

为了获得疏浚系统的状态空间模型，需要对方程组（2）的常系数进行参估计，因此，疏浚系统状态空间建模问题就转化为对状态方程组（2）的系数进行参数估计的问题。

2.2 基于BP神经网络的建模方法

BP神经网络[23]是一种多层前馈神经网络，通过任意选定一组权值，将给定的目标输出直接作为线性方程的代数和来建立线性方程组，解得待求权值，输入量从输入层经隐含层逐层计算，并传向输出层，每层神经元的状态只影响下一层神经元的状态，如输出层不能得到期望的输出，则转向误差反向转播过程。因此，可以采用BP神经网络算法解决以上问题。BP神经网络结构层数为2层，p个输入1个输出，神经原个数为q个，网络结构模型如图3所示。前向传播算法采用公式（3），传递函数采用纯线性函数purelin，即有 y=ψ[]x=x和y=φ[]

x=x，由于纯线性传递函数x与 y一一映射关系，可以只考虑权值项，阈值项为零，所以前向传播算法可以简化为式（4）。

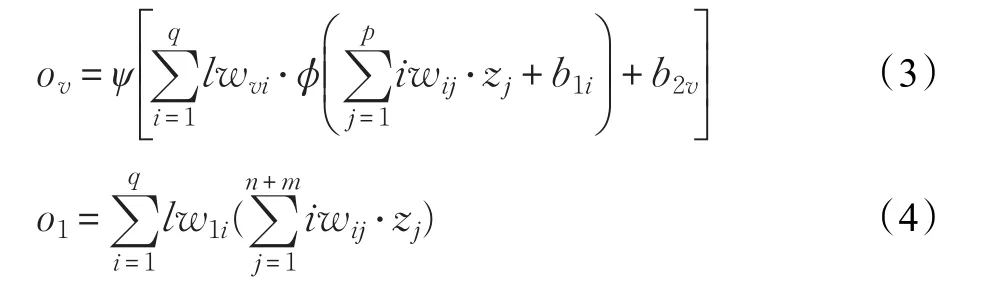
图3 BP神经网络结构模型

式（3）中，ov为输出层中第v个节点的输出，zj为第 j个输入，ψ为输出层传递函数，φ为输入层传递函数，lwvi为隐含层第i个节点到输出层第v个节点的权值，iwij为第 j个输入到第i个节点的权值，b1i为隐含层第i个节点的阈值，b2v为输出层第v个节点的阈值。

误差反向转播过程采用LM算法，性能函数采用均方误差函数，要确定方程组（2）的第一个方程的所有系数，只需要把 x1(t),x2(t),…,xn(t),u1(t),u2(t),…,um(t)作为输入样本，1(t)作为目标样本，经设计的网络训练可获得输出层权重lwvi和隐含层权重iwij，则确定第一个方程系数的算法如下。令：

BP神经网络的输出样本o1=ni()t，则有：

等式两边各项系数相等，即

在采用BP神经网络对样本数据进行训练中，合理地选择隐含层神经元的个数，可以提高网络训练的精度，因此在实际的网络设计中要充分考虑这一因素。疏浚系统状态空间模型构建流程如图4所示。

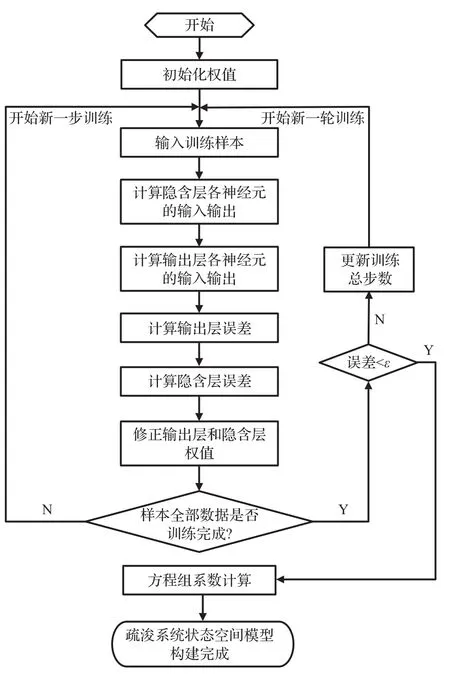
图4 疏浚系统状态空间模型构建流程图

3 疏浚泥浆浓度最优控制跟踪器的设计

在疏浚施工中，疏浚横移过程最重要过程之一，也是疏浚作业真正产生效益的过程，该过程中管道内输送的是泥浆，其他的过程，如斗桥收放、台车步进，收抛锚等过程都是辅助过程，在辅助过程中，管道内输送的是清水或管道内无输送。实际上，除换桩时挖泥船短暂停止外，在疏浚作业时，绞刀一直在作轨迹为弧线的运动。因此，横移速度是施工人员控制的重要目标，横移速度取决于“吃”泥量的多少：当泥浆浓度较高时，主机负荷增大，速度就慢一点；当泥浆浓度较低时，速度就快一些。基于以上的分析，选择横移速度作为离散疏浚系统的控制输入，泥浆浓度作为系统的输出，疏浚作业横移过程的状态空间模型为单输入单输出定常离散系统，离散系统状态空间模型为：

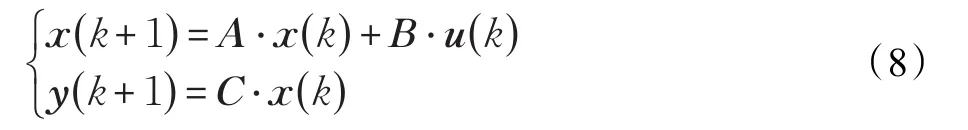
式中，x(k)为n维状态向量，在疏浚作业状态空间中，可以选择管道流速、泥浆浓度、绞刀功率、泥泵真空度、绞刀横移速度、绞刀步进量等作为状态变量，其初始状态为x(0)；u(k)为1维控制向量，对于疏浚横移过程，即为横移速度；y(k)为1维输出向量，为了设计泥浆浓度最优控制跟踪器，选择泥浆浓度为控制输出；A、B、C分别为n×n维、n×1维和1×n维的状态阵、控制阵和输出阵。

在管道流量变化较小的情况下，最大可能地提高泥浆浓度，可以实现疏浚产量最大化，因此，在疏浚施工过程中，保证管道输送安全的前题下，总期望泥浆输送浓度始终保持最大值，根据施工实际取期望泥浆浓度Cwmax,该期望泥浆浓度是管道输送安全的最大临界值，令期望输出z(k)=Cwmax，设计为稳态跟踪器，tf→∞，系统对终端状态无要求。则跟踪器性能指标为：

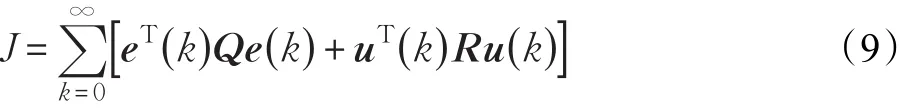
式中，跟踪误差e(k)=z(k)-y(k)，Q为1维的加权阵，R为1维的加权阵。跟踪器的性能指标函数第一项的作用是使疏浚系统输出尽量趋近于期望泥浆浓度Cwmax，第二项的作用是对系统控制能力的要求，是疏浚系统实时跟踪目标的同时，使能量消耗最小。疏浚横移过程线性二次型泥浆浓度最优控制跟踪系统结构如图5所示。

图5 疏浚横移过程线性二次型泥浆浓度最优控制跟踪系统结构图

对于稳态跟踪器，疏浚横移过程线性二次型泥浆浓度最优控制跟踪问题就转化为求式（10）黎卡提代数方程式的正定解，从而获得最优控制律u*()k的问题。

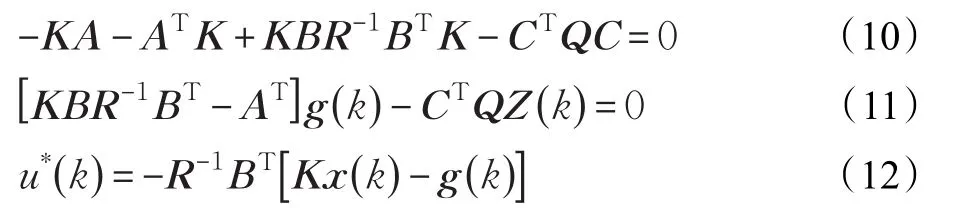
式中，K为式（10）黎卡提代数方程的正定解；g()t为式（11）的解。

在疏浚横移过程线性二次型泥浆浓度最优控制中，合理选取加权阵Q和R是跟踪器设计的重要一步，张洪钺[24]提出选取状态变量和控制变量的最大值的倒数作为加权阵的对角元素。则Q和R为标量，其初始值为：

疏浚横移过程线性二次型泥浆浓度最优轨迹方程为：

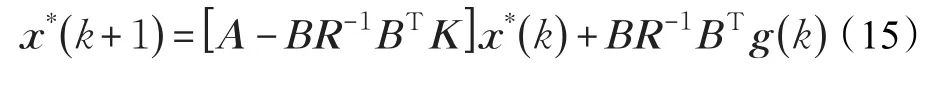
4 实例分析

4.1 BP神经网络训练与状态空间建模

实例采用某型绞吸挖泥船在工地上现场采集的实测数据，数据采集时长为3 584 s，采样周期为1 s，选取状态变量2个，x1(k)为泥浆浓度，x2(k)为管道流速和控制输入变量1个，u(k)为横移速度，可构建一个单输入单输出状态空间模型。现场实时数据如图6所示。

图6 现场实测数据

与经典控制理论的传递函数不同，状态空间描述是一个更加细致的过程，控制输入引起系统状态的变化，系统状态和输入的变化决定了系统输出的变化。状态变量和控制输入变量是疏浚现场采集的一定时间间隔的离散数据，每个状态变量的k+1时刻数据值作为目标样本数据。

选择BP神经网络输入样本数据为泥浆浓度Cw、管道流速V、横移速度Vs，目标样本数据分别为泥浆浓度、管道流速、绞刀功率的k+1时刻采样值，BP神经网络结构如图7所示，BP神经网络训练参数见表1。

图7 BP神经网络结构图

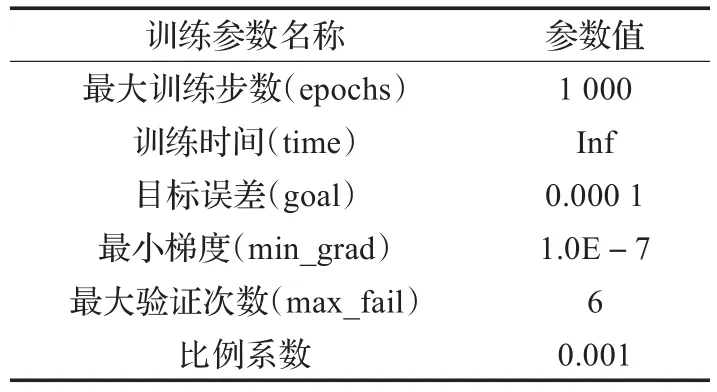
表1 BP神经网络训练参数表

经训练输入层到隐含层的权重可得iwji值，隐含层到输出层的权重为lw1i。权重值代入式（7）得：

泥浆浓度、管道流速、绞刀功率的BP神经网络训练仿真曲线及回归分析图如图8～图10所示。

图8～图10表明，仿真曲线与目标曲线的变化趋势相符，回归率达到0.8以上，结果表明输入样本能够较好预测目标样本，建立的系统状态空间模型是对实际疏浚系统的线性近似，从而有效地验证了建立状态空间模型与实际系统相似性。综上可得疏浚控制系统的状态空间模型如下：

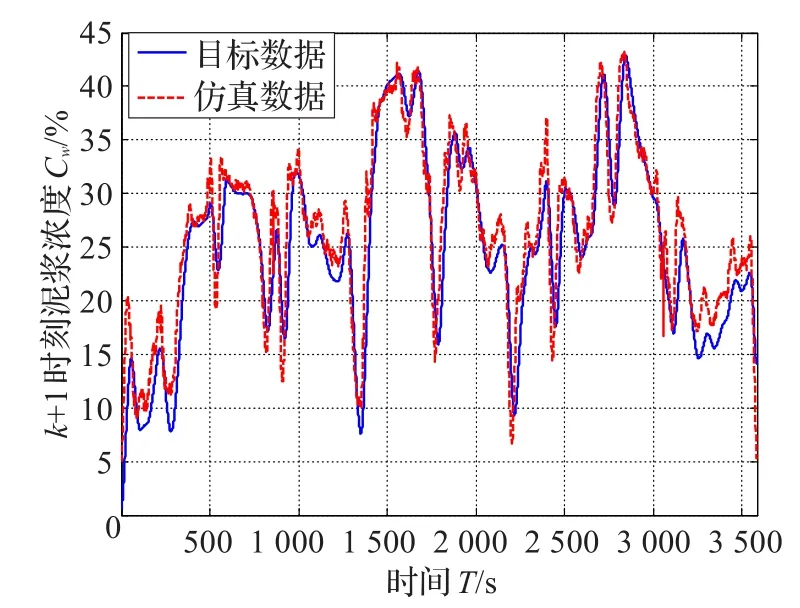
图8 （a）泥浆浓度神经网络训练仿真曲线图

图8 （b）泥浆浓度神经网络训练回归分析图

图9 （a）管道流速神经网络训练仿真曲线

图9 （b）管道流速神经网络训练回归分析图

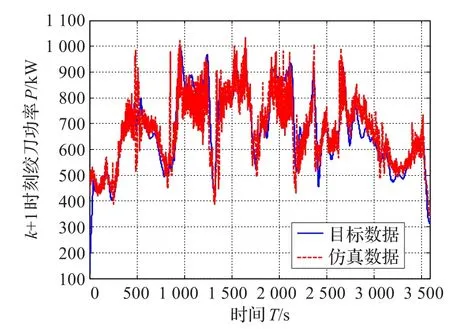
图10 （a） 绞刀功率神经网络训练仿真曲线

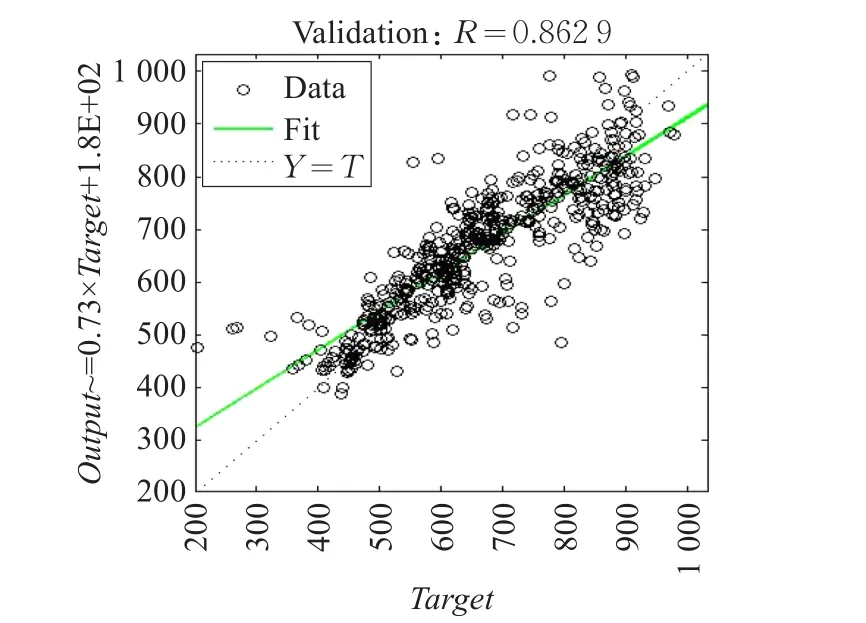
图10 （b）绞刀功率神经网络训练回归分析图

4.2 基于疏浚系统状态空间模型的泥浆浓度最优控制跟踪器仿真分析

疏浚控制系统是一个渐近稳定的系统，可以采用线性二次型的稳态问题进行分析。对于稳态问题，系统状态方程和性能指标中的加权阵需要满足以下两个条件，就可以得出常数的最优反馈增益阵。

条件1系统可控制或至少可稳，这一条件是为了保证性能指标的积分为有限值，计算Uc：rank( )Uc=3，所以系统可控。

条件2加权阵Q为正定或Q为半正定且(A,Q1)可观测，Q=QT1⋅Q1；取加权阵Q和 R初始值为：Q=Q满足正定要求。

取疏浚系统的期望浓度Cwmax=30，则理想输出z(t)=Cwmax=30，偏差量e(t)=30-y(t)；以上参数值代入式（9）得疏浚产量最优控制系统的性能指标函数为：

图11 （a）线性二次型最优控制跟踪器系统Bode图

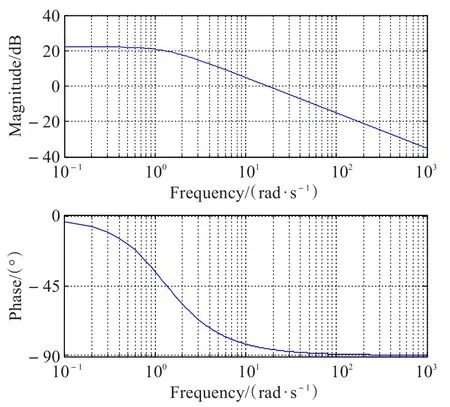
图11 （b）无最优控制的开环系统Bode图

图12 （a）线性二次型最优控制的开环系统的阶跃响应

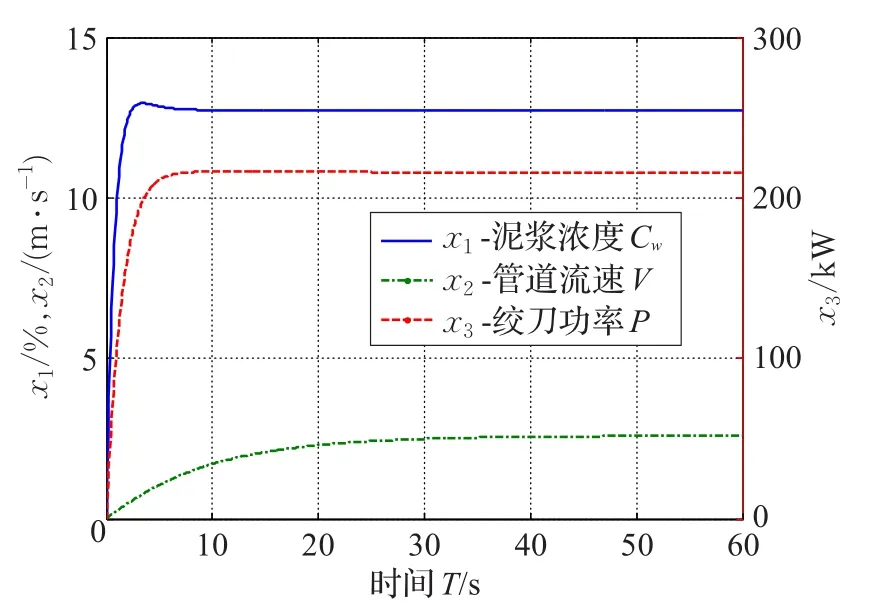
图12 （b）无最优控制的开环系统的阶跃响应

采用迭代算法求黎卡提代数方程（10）的解K和状态反馈增益阵G，将K和z(t) 代入式（11）得 g(t)=[0.406 5 0.014 5 -0.005 2]T，将 K 、g(t) 代入式（11）最优控制率为：

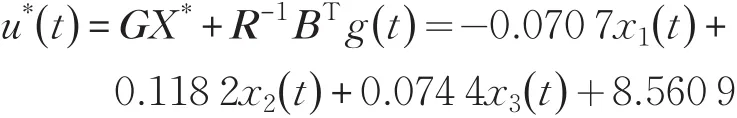
最优轨迹为：

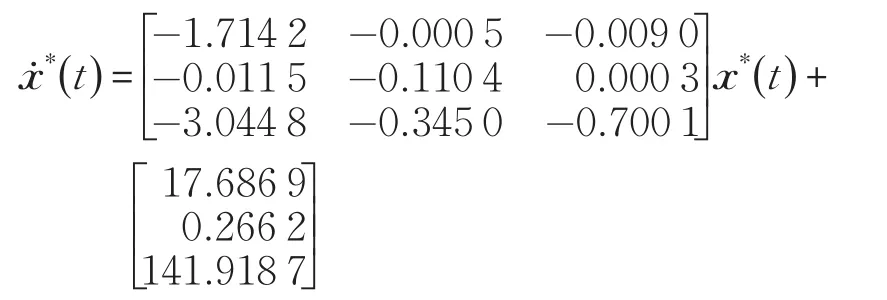
（1）线性二次型泥浆浓度最优控制跟踪系统的Bode图

无最优控制的开环系统的Bode图和线性二次型泥浆浓度最优控制跟踪系统的Bode图如图11所示。无最优控制时，相幅裕量为111.3°，幅值裕量为inf。说明该系统是开环稳定的。泥浆浓度最优控制时，相幅裕量为127.7°，幅值裕量为inf。相较开环系统，相幅裕量有了一定的提高，该系统为闭环稳定系统。

（2）线性二次型最优控制跟踪器系统阶跃响应

无最优控制的开环系统的阶跃响应和线性二次型泥浆浓度最优控制跟踪系统阶跃响应如图12所示，与开环相比阶跃响应的状态变量的响应幅度提高了5.5倍左右，说明跟踪及闭环控制反馈作用明显，且系统相较开环更稳定。

（3）线性二次型泥浆浓度最优控制跟踪器系统实际横移速度响应特性

使用疏浚作业实际施工现场采集的横移速度实时数据Vs作为线性二次型最优控制跟踪系统的控制输入，则无最优控制的开环系统和线性二次型泥浆浓度最优控制跟踪系统实际横移速度响应泥浆深度曲线如图13所示，采用线性二次型泥浆浓度最优控制跟踪系统的泥浆浓度提高约90%左右，说明该跟踪系统跟踪效果好，泥浆浓度提高显著，较好地克服了人工操作缺点。

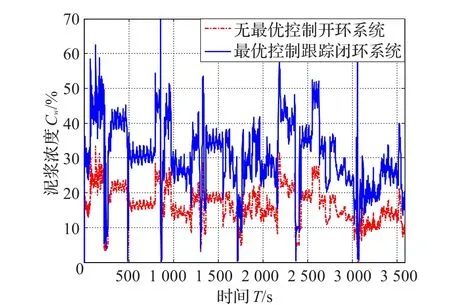
图13 实际横移速度响应泥浆浓度曲线

5 结语

疏浚作业过程是一个复杂动态变化过程，状态变量在相邻时刻状态转移变化规律无法用解析方法获得，且不同作业环境下各种疏浚系统状态转移变化规律有较大差别，因此，需要设计一种方法，构建反映这一规律的数学模型。文中提出一种基于BP神经网络的疏浚横移过程状态空间建模方法，建立了描述挖泥船疏浚过程各状态变量在相邻时刻状态转移变化规律的状态空间模型；在此模型基础上，设计了绞吸挖泥船横移过程线性二次型泥浆浓度最优控制跟踪器，应用于疏浚作业智能化控制中。在MATLAB仿真平台上进行仿真分析，对应用效果与挖泥船施工实时数据进行比较；结果表明：二次型最优控制跟踪器的控制稳定性好、响应快、滞后小，跟踪效果好，泥浆浓度提高显著，较好地克服了人工操作缺点。

[1]马桂荣.绞吸式挖泥船施工技术措施[J].治淮，2004（1）：29-36.

[2]Vlasblom W J.Production quality control during dredging worksatthe new Hong Kong airport[C]//Texas Aamp;M3 1st Annual Dredging Seminar，Louisville，Kentucky，1999：16-18.

[3]Baadbaart J，Mourik M W.Effieient dredging：the next generation[J].Ports and Dredging，2004，162：20-23.

[4]Miedema S A.Production estimation based on cutting theories forcutting watersaturated sand[C]//Proceedings of WODCONXVII，Amsterdam，The Netherlands，1995：105-112.

[5]唐建中，王庆丰，张麒，等.绞吸式疏浚作业专家系统理论与实验研究[J].中国机械工程，2007，18（18）：2218-2222.

[6]闭治跃.挖泥船泥浆管道输送系统效率优化与控制研究[D].杭州：浙江大学，2008.

[7]倪福生，赵立娟，齐帜，等.粗砂水力输送多峰阻力特性[J].中国港湾建设，2010（1）：23-27.

[8]倪福生，赵立娟，顾磊，等.绞吸挖泥船疏浚仿真研究[J].系统仿真，2012，24（11）：2271-2274.

[9]徐立群，蔡慧官，倪福生.挖泥船泥沙含量问题的探讨[J].江苏船舶，2006，23（1）：1-3.

[10]蔡景勇，倪福生.基于BP神经网络的绞吸挖泥船产量特性研究[J].河海大学常州分校学报，2010（6）：35-40.

[11]李志刚.基于横移阻力的绞吸挖泥船横移自动化设计研究[D].江苏常州：河海大学，2015.

[12]马亚生，倪福生，Miedema S A.绞刀片大角度切削水饱和沙的力学模型[J].河海大学常州分校学报，2006（3）：59-61.

[13]潘英杰，杨启，汤晶.基于二维切削理论的绞吸式挖泥船绞刀头载荷分析[J].船海工程，2009，38（2）：35-39.

[14]王其松，严军，邓家泉.绞吸式挖泥船产量优化研究[J].水运工程，2013（3）：48-55.

[15]Ljung L，Vicino A.Special issue on system identification[J].IEEE Transactions on Automatic Control，2005，50（10）.

[16]Ghahramani Z，Roweis S.Learning nonlinear dynamical systemsusing an EM algorithm[C]//NeuralInformation Processing Systems（NIPS 1998），1998：431-437.

[17]Schon T，Gustafsson F.Particle filters for system identification of state space models linear in either parameters or states[C]//Proceedings of the 13th IFAC Symposium on System Identification，The Netherlands，2003：1287-1292.

[18]Andrieu C，Doucet A.Particle filtering for partially observed Gaussian state space models[J].Journal of the Royal Statistical Society，2002，64（4）：827-836.

[19]Gibson S，Wills A，Ninness B.Maximum-likelihood parameterestimation ofbilinearsystems[J].IEEE Transactions on Automatic Control，2005，50（10）：1581-1596.

[20]熊建华，罗芬，戴虹，等.基于GRM模型的BP神经网络参数估计[J].心理科学，2014，37（6）：1485-1490.

[21]阮士平.基于LM-BP算法的综合水质评价研究[J].西安理工大学，2003（11）：50-56.

[22]欧阳林群.提高多层前向神经网络泛化能力的讨论[J].南平师专学报，2007，26（2）：60-63.

[23]周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005：88-89.

[24]张洪钺，王青.最优控制理论与应用[M].北京：高等教育出版社，2006.

ZHU Wenliang1，2,NI Fusheng1，2,WANG Suhong3,YIN Fei3

1.College of Harbor Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China 2.Research Center of Dredging Technology,Ministry of Education,Hohai University,Changzhou,Jiangsu 213022,China 3.Lianyungang Municipal Water Conservancy Bureau,Lianyungang,Jiangsu 222006,China

Design and implementation of tracker for dredging slurry concentration optimal control.Computer Engineering and Applications,2017,53（21）：263-270.

During the dredging operation,the main operation parameters of cutting suction dredger are decided by operators,whose personnel experience and theoretical level is comparatively large difference.The operators make a decision according to their own experience,so the manual operation is far lower than expected yield,lower efficiency,higher operation cost,poorer operation quality.In order to overcome these shortcomings,this paper puts forward a dredging state space modeling method based on BP neural network,and designs linear quadratic optimal control tracker,which is applied to cutter suction dredger swing process control and is an effective method of the intelligent control instead of the manual operation.The simulated result shows that the linear quadratic optimal tracking system has more stabilization,quicker response,smaller hysteresis,better tracking of the desired output,and overcomes the drawback of manual operation.

dredger;dredging system;state space;model;quadratic;optimum control;strategy

A

TP273

10.3778/j.issn.1002-8331.1604-0209

朱文亮（1974—），男，博士，高级工程师，研究领域为船舶自动化、机器人、智能装备，E-mail：zwliang2001@qq.com；倪福生（1961—），男，博士，教授，研究领域为疏浚技术、疏浚工艺与仿真、两相流；王素红（1976—），女，工程师，研究领域为自动控制；尹飞（1976—），男，高级工程师，研究领域为自动控制。

2016-04-15

2016-08-12

1002-8331（2017）21-0263-08

CNKI网络优先出版：2016-08-18,http://www.cnki.net/kcms/detail/11.2127.TP.20160818.1551.038.html