节点层次化的二进制文件比对技术
2017-11-28肖睿卿刘胜利孙豪彬
肖睿卿,刘胜利,颜 猛,肖 达,孙豪彬
1.数学工程与先进计算国家重点实验室,郑州 450001 2.西安报业传媒集团,西安 710002
节点层次化的二进制文件比对技术
肖睿卿1,刘胜利1,颜 猛2,肖 达1,孙豪彬1
1.数学工程与先进计算国家重点实验室,郑州 450001 2.西安报业传媒集团,西安 710002
当前二进制文件比对技术主流是以BinDiff为代表的结构化比对方法,存在结构相似导致的误匹配、分析耗时较高的问题。针对该问题提出一种基于节点层次化、价值化的匹配方法。通过提取函数节点在函数调用图中的层次与函数在调用网络中的价值,对层次模糊的节点提供了节点层次估算算法,最后递归匹配节点。实验表明,该方法避免了结构相似导致的误匹配,其时耗低于结构化比对工具Bindiff的1/2,节点匹配数量减少在15%以内。该方法可有效提高嵌入式设备固件的跨版本相似性分析效率。
二进制文件比对;层次分析;节点价值;结构化图形
1 引言
二进制文件相似性比对是逆向工程中一种重要的静态分析方法,用以刻画二进制文件之间的关联性,常用于软件剽窃检测、恶意程序同源性检测、补丁比对等领域。随着软件功能的复杂化,部分软件的程序规模不断提高,传统二进制文件相似性分析方法在效率和准确性方面面临新的挑战。
二进制文件比对的方法主要分为两大类:指令级比对和结构化比对。指令级比对包括:二进制字节比较、反汇编后文本比较、基于汇编指令图形化比较等[1]。二进制字节比较优势在于比对粒度细,但没有基于指令语义比较,微量变化即影响相似性识别(如:程序仅替换操作寄存器且功能不变)。反汇编后文本比较减轻了比较的工作量,同时兼顾字节间的联系,以汇编的角度来比对相似性。文献[2]提出基于汇编指令图形化比较主要是指基于汇编指令的相似性图形比较,此种方法通过将每条指令设为图形的节点,通过优化CFG图以获取结果。2004年,Halvar Flake于文献[3]提出了基于结构化图形的比较方法,该方法通过将文件结构图形化,利用控制流图(CFG)比较,函数调用图(FCG)进行签名并比较,提升了对程序相似比对的性能。文献[4]在前文基础上引入了属性的概念,通过属性提高比对效率。文献[5]亦在结合指令比较和结构化比较的优势优化比较效果。文献[7-11]中主要在依靠结构化签名和属性进行优化,并将算法加以实现,如魏强等人通过可信基点优化了匹配节点传播算法,但本质都是在结构化签名和属性两个方面进行扩展,签名重点围绕在CFG图。此后,结构化比较又逐步衍生出了,基于API调用序列比较等方向。文献[12]阐述了指令重排与指令归并减少了编译器优化带来的匹配难度。随着软件检测需求不断增加,开始出现针对软件特别是恶意软件比对的研究。文献[13]引入了相似度衡量方法。文献[14]将比对的侧重倾向于FCG图,这不同于以往的二进制文件比对,特别是补丁比对的侧重CFG图。文献[16]利用确定子图和相似子图进行基于子图的相似性分析,提高了对恶意程序检测的效率,脱离了三元组签名的制约。但二进制比对大体都是在围绕控制流图,函数调用图,以三元组〈节点数,边数,子图调用数>及图所含不同属性(如:出入度,所含特殊数据)为基础进行比对。这种技术路线存在以下问题:
(1)三元组中多为数量特征,节点出度、入度等附加属性也多是如此,当程序规模较大,这种单节点属性效果欠佳。
(2)编译器的不同会导致函数节点的结构形成上产生一定的出入,即使语义相同,因为优化等因素的影响,也可能产生不同结构的编译结果。
(3)传统匹配需要提供匹配节点作为初始化的参数,以降低函数匹配工作量,同时提高匹配精度。对于嵌入式等程序,规模较大,本身无公开API,可供参考的外部属性(如:API,字符串)相对整个程序规模而言较少,初始匹配节点影响范围较小,需要更多的利用结构图本身的信息。
针对现有方法的不足与实际问题的需求,本文在函数调用图基础上,提出基于节点价值与层次的刻画方法,进行二进制文件相似性分析。
2 相关概念
定义1(函数调用图)函数调用图(Function Call Gragh,FCG),由 G=(VG,EG)构成的有向图表示。其中,VG表示节点集,每个节点对应一个函数VG={fi|1≤i≤n,i∈Z},其中Z为整数集,n为函数个数;EG为边集,表示函数调用关系的全集,EG⊆VG×VG,由序偶组成,函数fi调用了若边集EG存在元素则说明函数 fi调用了函数 fj。
为便于后续定义的描述,参考树结构的定义,令集合G中入度为零的节点作为FCG的根节点。令集合G中初度为零的节点作为FCG的叶子节点。称 fi,fj两节点存在父子关系,该边为父节点 fi的度边、子节点 fj的入度边。需要说明的是,在实际分析过程中,由于间接调用的存在,部分函数虽然代码逻辑上并不是根节点,但在函数调用图中入度为零,无法与代码逻辑上的根节点区分,因此函数调用图在此种情况下将以森林的形式存在。
定义2(函数调用序列)若函数 fa是 fb的祖先,则存在调用序列表示一条从函数φ1到函数φn的调用路径,x表示调用序列的序号用以区分调用序列,φ表示函数节点,其角标表示函数节点在本函数调用序列Seqx( )fa,fb中的次序,设有映射关系ρ满足公式(1),则调用序列满足公式(2)。
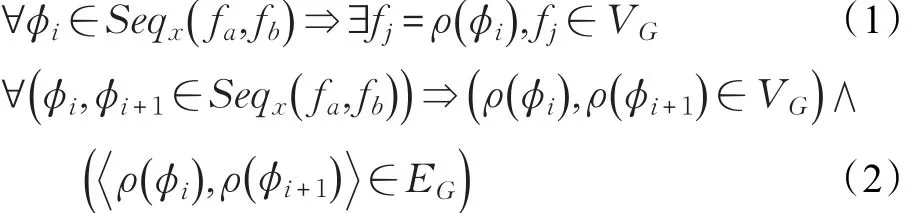
即,对于调用序列Seqx( )fa,fb内的任意两个连续元组成的序偶,一定属于边集EG。存在次序不同的两个位置代表一个函数,见公式(3)的情况。如果满足公式(4),称调用序列为无重调用序列SeqNx( )φ1,φn。

|Seqx( f1,fn)|表示路径Seqx( f1,fn)的长度,若,称Seqk( fa,fb)为函数fa到 fb的最短函数调用序列,其中 fa,fb∈VG。
定义3(节点深度)对于一个节点 fn,如果有根节点 fa,且 fa,fn之间存在无重调用序列SeqNx( fa,fn),则称路径长度 | SeqNx( fa,fn) |为此条路径下节点 fn的深度Dp(S eqNx( fa,fn) )。对于所有根节点到此节点路径下深度的均值,称为该节点 fn的深度Dp(fn)。根节点深度为0。
定义4(节点高度)对于一个节点 fn,如果有叶子节点 fb且 fn,fb之间存在无重调用序列SeqNx( fn,fb),则称路径长度 | SeqNx( fn,fb) |为此条路径下节点 fn的高度Hi(S eqNx( fn,fb) )。此节点到所有叶子节点路径高度的均值,称为该节点 fn的高度Hi(fn)。叶子节点高度为0。
定义5(节点依赖度)对于一个节点 fn,被s个节点直接调用累积x次,若某一节点 fm对 fn直接调用次数为 y次,则Rely( fm,fn)=x/y代表节点 fn对于 fm的依赖度。对于依赖度的分布可以有效观察出函数功能主要服务倾向。
定义6(循环调用节点)如果函数调用图存在调用序列Seqx( fa,fa),则称节点 fa为循环调用节点。调用序列Seqx( fa,fa)称为 fa的一条循环路径。如果调用序列满足公式(5),则称该序列为单纯循环路径SeqSx( fa,fa),反之称为复杂循环路径SeqCx( fa,fa)。
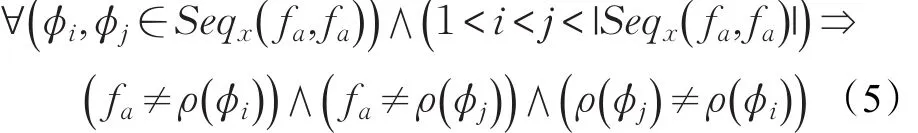
3 基于节点层次与节点价值的匹配方法
本方法的输入是两个程序的二进制文件A,B。首先,从两个二进制文件中分别提取函数调用关系图GA,GB。通过节点层次记录算法,对节点所处高度Hi与深度Dp进行记录。而后,通过节点价值评估算法,对节点在调用图中的价值进行评估,并对节点间的依赖关系进行分析。最后,利用节点层次、节点价值、节点依赖关系进行程序匹配。
基于节点层次与节点价值的匹配方法减少了对输入信息的依赖,主要利用函数在函数调用图中结构化的属性。
3.1 函数调用图提取
实际条件下,由于程序的二进制文件可能存在一定的反分析保护措施,需要对程序进行预处理。但文件脱壳等预处理方法与本文主题关联不大,在此不做深入讨论。本文默认将要比对的二进制文件A,B为无反分析保护或已解除反分析保护的形态。函数调用图最终以矩阵来表示,使用二维数组进行存储。提取过程如下:
(1)识别二进制文件中的函数,统计函数数量n,构建 n⋅n矩阵 Matrix()G ,用二维数组G[n+1][n+1]表示,将其中所有分量初始化为0。
(2)为每个函数单独分配一个独立的序号n,(0<i<n+1),如果函数 fi直接调用 fj,且 fi调用 fj的次数为s次,则将G[i][j]的值替换为 s,并将G[i][0],G[0][j]的值各加s,分别表示 fi调用子函数次数和,fj被调用次数和。
3.2 基于节点层次的分析方法
基于节点层次的分析方法主要需要针对节点在函数调用图中的高度和深度进行分析,并形成节点深度矩阵和节点高度矩阵。
3.2.1 非循环调用节点深度计算
根据节点深度的概念,构建节点(n+1)⋅(n+1)深度矩阵Matrix(D p),采用二维数组Dp[n+1][n+1]存储节点深度,将其中所有分量初始化为-1。
计算节点深度矩阵有两种方法,第一种方法主要依靠父子关系从子节点上溯,随机取一个深度未知的节点fj。如果 fj存在未知深度父节点 fi,则计算 fi深度。如果 fi深度无法计算则递归调用父节点深度计算过程。
第二种方法主要依靠逐层计算的思想,首先对所有根节点的深度标注为0,而后对所有已知深度节点的子节点进行遍历,如果子节点的所有父节点深度已经明确,计算出该子节点深度,不断扩大已知节点的范围,直至计算出所有节点的深度。
节点深度计算公式如公式(6),由于G[n+1][n+1]数组初始置为0,则满足公式(7)。
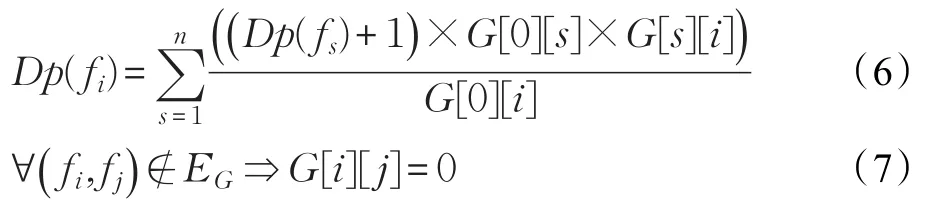
由于节点深度是基于父节点的深度已知完成的。当函数调用序列Seqx不是无重调用序列SeqNx时,即存在函数循环调用至自身的情况时,必然有节点无法求出深度。在此,先提出非循环调用节点的深度计算算法,考虑到函数调用图中存在循环调用节点,如果使用方法一需要解决上溯去循环的问题,因此使用方法二。流程如下:
(1)构建二维数组Dp[n+1][n+1]用以存储节点深度。初始化二维数组,对所有节点赋值-1。定义已知节点缓冲区,一维数组S[n+1],初始化为0。定义结构体Ns,记录待处理节点信息,其中包括节点序号Ns.Index,未知深度父节点序号数组Ns.Uf[n+1],初始化为-1,未知父节点数量Ns.Numf。Ns以链表形式存在。
(2)搜索G[0][1]到G[0][n],即所有函数的入度,如果节点 fi入度为0,表示此节点为根节点或间接调用节点,对 Dp[0~n][i]赋值为0。
(3)搜索 Dp[0][1~n],如果 Dp[0][j]>0,说明该节点深度已知,若S[j]为0,表示该节点未处理过,执行下一步,反之表示处理过。若所有深度已知节点都已经表明被处理过,则结束。
(4)遍历Ns所在链表,本节点是否为某链表节点的未知父节点,如果是,则未知父节点数量Ns.Numf减1,并把Ns.Uf[i]置为0。调整Ns链表顺序,将Ns.Numf小的靠前放置,如果Ns链表节点(Ns.Index=k)没有未知父节点,则从链表中去掉,并依据公式计算该函数节点的深度,存放在Dp[0][k]。
(5)在G[0][1~n]中逐个检索 fj的子节点,对于检索到的子节点 fk,若Dp[0][k]为-1,表明未计算出该节点深度,将 Dp[j][k]置为 Dp(fj)+1,在 G[1~n][k]中检索 fk的其他父节点,如果不存在深度未知父节点,则计算 fk深度存放于Dp[0][k]。否则,统计该节点的未知父节点信息,申请新的Ns链表节点,将未知父节点 fi对应的Ns.Uf[i]置1,插入Ns链表。检索完毕后,跳回执行步骤(3)。
此时,获取所有深度未知节点,可以形成一张子图G1,如果从G1中再计算出图中非循环调用节点的节点高度,并将G1中的高度已知节点剔除,可以形成一张循环调用子图G2,G2中的任何节点都可以找到一条调用序列回到节点自身。
3.2.2 循环调用节点深度计算
一个循环调用节点,可以存在多条循环路径。而一条循环路径中选择不同的节点作为深度值最小的点(下文称“基点”),将形成不同的深度矩阵。如果在子图G1中存在一条单纯循环路径与其他循环路径不相交,那么子图中将需要至少两个循环路径的基点来完成深度矩阵Matrix(D p)。解决循环调用路径中节点的深度的问题在于确定合理的基点。
要确定基点,首先要确定目标处理的循环路径,优先选择路径较长的单纯循环路径,以减小后续运算的规模。循环调用路径的基点必须具备深度已知父节点。函数调用图中,靠近根节点的节点一般入度较低、出度较高,而靠近叶子节点的节点一般入度较高,出度较低。函数调用图整体接近于梭形。因为根节点端要分支出多种逻辑情况,而叶子节点端函数处理最终会回归原子性的函数操作,如API,库函数。
由于当前是在计算函数的深度调用图,因此基点选取考虑以下条件:
(1)节点具备已知深度父节点,且对未知父节点的依赖度之和控制在一定范围内。
(2)节点的已知父节点平均深度较小。
(3)节点的出度较大。
(4)计算两个基点互相的依赖度,依赖对方较小的节点处于深度值较小的位置,也就是更接近根节点。
(5)在实际比对过程中,如果程序规模较大,可能出现从多个节点中筛选基点的情况。
在确定了基点 fi后,将不再考虑未知深度父节点对该节点的深度影响,对Dp[1~n][i]值不为正的点置-1,基点将通过已知深度父节点计算基点的深度值,并计入数组Dp[0][i],同时,由于基点忽略了未知深度父节点,基点入度将有所改变,将Dp[i][0]处填写已知深度节点的入度和。
同时,对于计算节点深度的公式进行修改,如公式(8)。
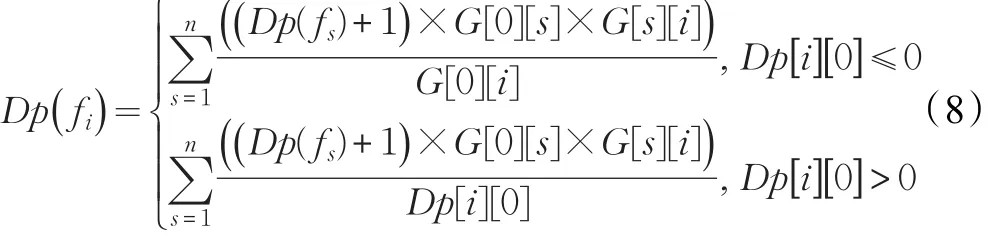
此后采用前文无循环调用节点的节点深度计算算法,继续完善深度矩阵,如果深度矩阵仍有节点深度未知,则说明仍有循环路径存在,继续确定循环路径基点,重复上述步骤,直至完成深度矩阵。
节点高度矩阵Matrix( )Hi的构建参看节点深度矩阵构建流程,以叶子节点为起始点,其高度初始赋值0,高度调用图存储数组Hi[n+1][n+1]。
3.3 基于节点价值的分析方法
通过节点的出入度,可以基本地反应节点的被调用和调用子节点情况。但是,节点在程序中的重要性并不能得以直观体现。补充定义如下。
定义7(节点价值)使用四元组表示,Val()fi={Fnum,Snum,T,Iv}。Fnum表示父节点数量,Snum表示子节点数量,价值类型T表示价值偏重,计算公式如公式(9),T>0.5表示为收敛倾向,T<-0.5表示为发散倾向,其他情况表示均匀倾向。Iv表示节点间接价值。

节点间接价值Iv计算流程:
(1)将 fi所有父节点与 fi节点归并为一个新节点fi',并将其父节点所有数据计入新节点 fi'。构建新的函数调用矩阵Matrix( )G1存储信息。
①对于任何 fi的父节点 fj,提取函数调用矩阵中的G[1~n][j]的值,并将每个值累加到新矩阵Matrix( )G1对应列 G1[1~n][i]中。
②对于任何 fi的子节点 fk,提取函数调用矩阵中的G[1~n][k]的值,并将每个值累加到新矩阵Matrix( )G1对应列 G1[1~n][i]中。
(2)计算节点 fi'的入度和SumI( fi')与出度和SumO( fi'),并求出函数调用原矩阵Matrix(G)的入读和SumI(G)出度和SumO(G )。节点 fi的间接价值Iv计算公式如公式(10)。

节点间接价值Iv能够反应节点服务的父子节点在整个调用图中的价值。即使存在两个节点价值相近,但是节点服务对象在函数调用网络的存在价值差异。
针对不同规模的两个程序,定义7中的父子节点数量会受函数总数量的影响,导致可比性较差。因此,在进行比较的过程中,对节点价值的描述需要进行调整。
在此,对定义7做出补充,基于相对深度(或高度)测算的节点价值,将定义其中的Fnum,Snum做出修改,用父子节点数量在同层次节点数量中占比来表示。节点是否为同层次,可以通过节点深度(或高度)上下取整来确定。向上或向下取整只能选择一个,并保证整个调用图计算过程中只选用此方向。
当两个程序同节点层次的节点数量相差较大时,使用占比数据已经无法满足需求,此时,可以采用Findex,SIndex替代Fnum,Snum,分别表示父子节点数量在同层次节点数量占比值的大小排序,通过纵向的大小关系来完成比对。
3.4 结合节点层次与节点价值的匹配方法
在此,对函数节点定义进行补充。
定义8(节点签名)为便于后续分析,对函数调用图中的函数节点三元组定义进行扩展,由N(fi)={BNum,ENum,SFNum,Dp,Hi,Val(fi)}表示,其中BNum表示节点 fi基本块数量,ENum表示函数控制流图CFG的边数,SFNum表示节点子函数数量,这三个变量可以参看文献[3]。Dp表示节点深度,Hi表示节点高度,Val(fi)表示节点价值。
3.4.1 初始匹配点与扩展匹配算法
传统的匹配算法是通过输入被比对程序的已知匹配点作为初始匹配节点开始,通过在匹配节点集的子节点集合中寻找新的匹配节点来扩大匹配节点集,直到匹配完成。如果程序主要调用方式为直接调用,且有明确的程序入口点,使用这种方法具备较高的效率。如果程序规模较大,存在大量间接调用,无明确入口点,匹配的效果受匹配点所处节点高度、节点价值影响较大。
在本文中,主要通过确定同一层次的节点加入待匹配节点集,通过比对待匹配集内不同节点的价值,基于节点价值与基本三元组信息完成匹配。每向下分析一层,将上层匹配节点从待匹配集合去除。
3.4.2 同程序内函数相似性
节点价值是用以描述函数的重要特征。当同程序内多个函数具备相似的父子节点关系时,不同节点的节点价值趋同和节点层次趋同将对跨程序逐函数匹配产生干扰。通过预处理,可以对此种情况加以利用。
定义9(公共父节点)对于函数调用图G,满足公式(11),则称 fi是 fj和 fk的公共父节点。对于函数调用图G,满足公式(12),则称 fi是 fj和 fk的公共子节点。
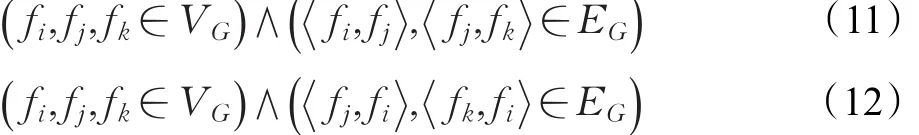
如果两个函数节点 fj和 fk的公共父节点数量在各自父节点数量中占比80%以上,则认为两函数具备相似的调用关系。通过这种方法,可以获取具备关联性的函数组合[fj,fk]。当函数组合中的某一节点的控制流图CFG结构信息有一定变动时,可通过组合中另一函数的匹配来提高匹配效率。
当两个函数的子节点具有相似性时,说明两个函数的功能具有一定相似性。考虑到子函数可能同时服务多个父函数,因此,衡量函数节点公共子节点的相似性,应当结合子函数调用次数。相似度计算公式如公式(13),表示 fj,fk的公共子节点对前者的相似度。
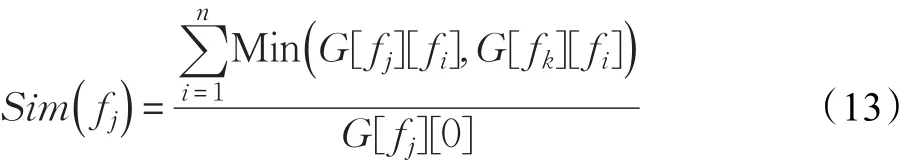
当几个函数的公共子节点相似度互相达到80%以上,则认为几个函数功能基本相似。如果其中某个子函数对父节点的依赖度主要集中在这几个父函数中,则认为该子函数具备核心功能。同时可以用公共子函数修正函数所处层级,将公共子函数的层次放在几个父函数层次之下。
3.4.3 二进制文件相似性度量流程
(1)选择二进制文件 A,B形成函数调用关系图(FCG)。
(2)检测两个文件中各自父子节点的相似函数,确定关联函数组集与近似功能函数集。
(3)进行二进制程序层次分析,确定函数高度矩阵和深度矩阵,同时利用近似功能函数集进行层次修正。
(4)完成二进制程序节点价值分析。
(5)进行关联函数组匹配,将两个二进制文件中的关联函数组优先测试匹配。
(6)以关联函数数组匹配点为输入,从根节点或叶子节点开始,逐层次进行节点匹配,方向为高度递增或深度递增,将每一层不匹配节点融入下一层次继续匹配。
4 实验结果分析
在Windows平台上使用Python语言,利用IDApython在IDA pro上进行函数调用关系的抽取。使用C#语言完成后续工作,包括函数调用关系图构建、节点层次分析、节点价值分析、二进制文件相似性分析。
4.1 验证性实验结果分析
实验主要验证文中方法能否有效检测二进制文件相似性以及函数匹配。通过实验,该方法能够有效检测出相似函数,针对规模较大的文件效果良好。
实验使用ELF文件Adventerprisek9-Mz 124-2 T与adventerprisek9-mz.123-11.T进行检测。其中,文件1节点数量147 011,文件2节点数量133 493,共检测出匹配节点115 019个。
4.2 对比实验结果分析
二进制文件比对工具Bindiff和PEdiff是经典的两款文件相似性比对工具,由于文件格式以及目标平台的不匹配,无法使用PEdiff进行匹配,因此,本文主要采用Bindiff进行匹配。比对文件与4.1节相同,结果如图1。

图1 Bindiff4.2比对耗时23 222 s
采用本文方法主要提取节点层次信息、节点价值信息,最后完成匹配,如图2~4。其中层次信息提取耗时7 860 s,节点价值信息提取耗时266 s,匹配耗时568 s。

图2 层次信息提取
图3 价值信息提取

图4 匹配耗时
通过比对Bindiff4.2的匹配结果与本文方法匹配结果,如图5,发现本文方法可以避免因函数结构相似导致的错误匹配。

图5 BinDiff4.2匹配函数0x8002652c结果
0x8002652c和0x80e6cc0c是BinDiff4.2匹配的两个函数,如图6、图7,相似度0.76,可信度0.78。两者结构一致,但是只通过特征字符串即可判别两个函数实际并不一致。利用本文的方法,可以得出函数0x8002652c所匹配的函数为0x80d0ae04,如图8。虽然函数结构具有较大差异,但函数语义一致。
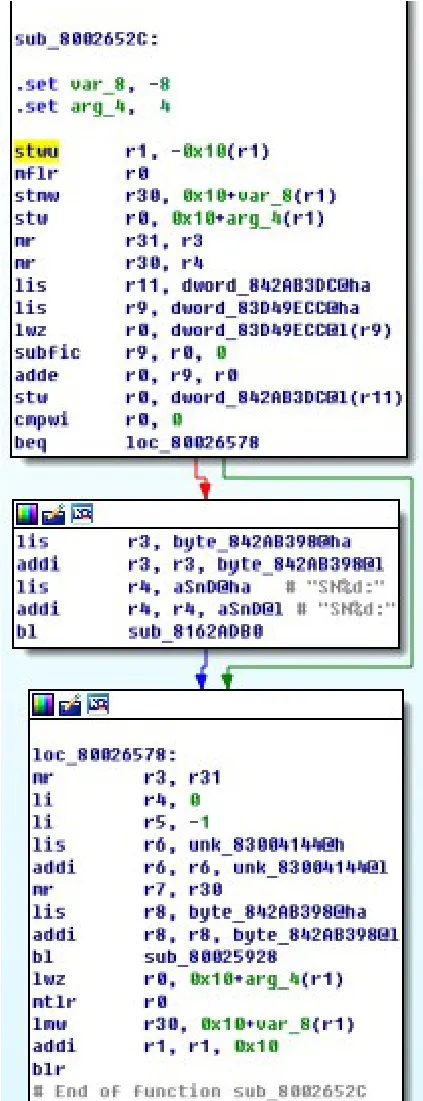
图6 函数0x8002652c
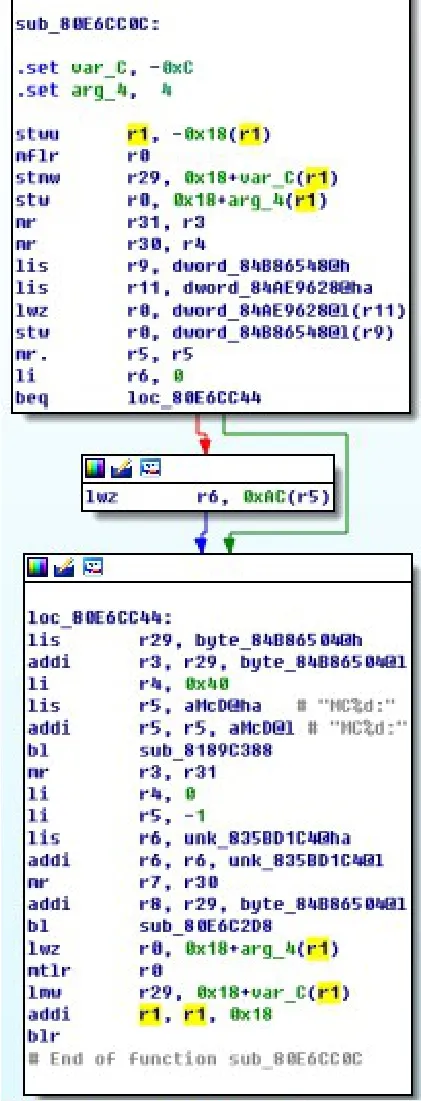
图7 函数0x80e6cc0c

图8 函数0x80d0ae04
根据上个函数在BinDiff中的相似度可信度排序可以确定,约有13 000个函数节点可信度低于此。在衡量本文方法不匹配点和Bindiff4.2结果不匹配点的过程中,如果以可信度低于0.78作为不匹配点不够客观。故Bindiff不匹配节点数量的衡量,取其衡量结果中相似度低于0.5的节点数量。
对于匹配率采用匹配节点数与节点总数较小值的比值作为结果。不匹配率采用不匹配节点数与节点总数较小值的比值作为结果。通过比对发现,Bindiff4.2中除了相似度匹配和不匹配节点,还有一部分节点被丢弃了,本文方法中也对不具备调用关系的节点进行了丢弃,此类孤立节点需要另行处理,本次前两个实验中,将被遗弃节点计入不匹配点。对于本文方法的匹配时间衡量,采用节点层次计算时间、价值计算时间、匹配值时间之和作为整个匹配过程的耗时。两种方法的匹配结果见表1、表2、表3。表1为大规模程序实验,表2为小规模程序实验,表3为版本大跨度实验。

表1 Bindiff4.2与本文方法对Adventerprisek9-Mz 124-2 T与adventerprisek9-mz.123-11.T匹配结果

表2 Bindiff4.2与本文方法对ds-121-5与ds-122-5匹配结果

表3 Bindiff4.2与本文方法对ik8o3s-122-5与ik9o3s3-123-1a匹配结果
受程序规模影响,以往进行二进制文件比对特别是补丁比对的实验,比对函数数量基本在千级以内,差异并不明显。实际,BinDiff在处理程序函数数量较高时,比如,函数规模达到10万级别,时间消耗明显。使用文中方法有效降低了比对时间,提高了效率,匹配率也接近Bindiff的匹配率,其中在小版本跨度大规模程序实验时,效果最好。
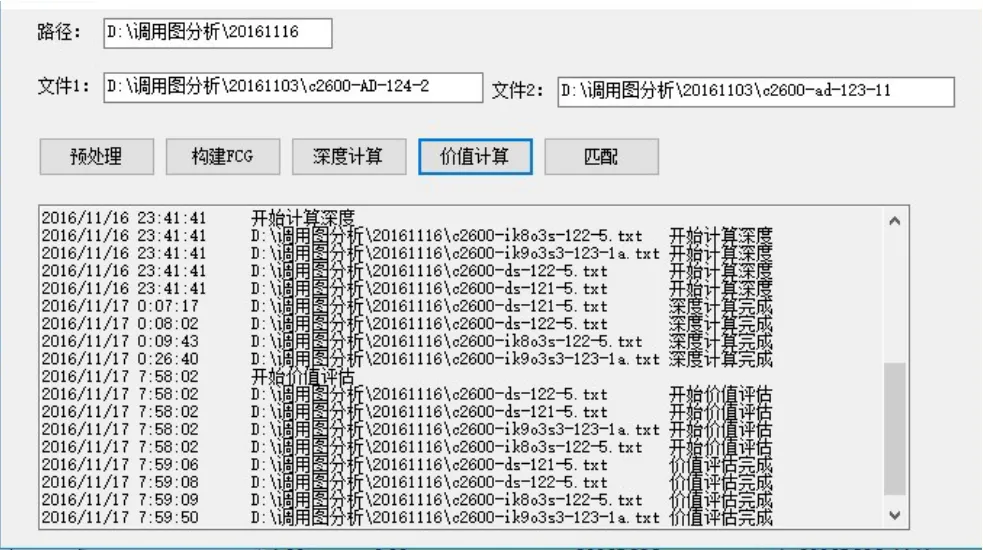
图9 ds-121-5、ds-122-5、ik8o3s-122-5、ik9o3s3-123-1a匹配过程
5 总结与展望
本文提出的基于节点层次和节点价值的相似性检测方法依靠函数调用图进行分析,根据需要分别测算了节点在调用图中的深度、高度,通过节点的父子节点种类,形成了关联函数组和近似功能函数,对节点的高度深度测算进行了修正。同时,针对节点在调用图中的价值,通过直接和间接关系分别在同层次和全局进行了评估。通过节点价值分析以及节点层次分析,提高了二进制文件函数匹配的效率。下一步将以此方法为基础,进一步优化,尝试完成对不同函数数量级的文件进行相似性比对,以期克服函数层次分析受结构影响的缺点,为在不同级别程序中寻找库函数提供支撑。
[1]韩锋.基于结构化图形的二进制文件比对技术研究[D].北京:北京林业大学,2013.
[2]Sabin T.Comparing binaries with graph isomorphism[EB/OL].Bindview.[2004].http://www.bindview.com/Support/RAZOR/Papers.
[3]Flake H.Structural comparison of executable objects[C]//IEEE Conference on Detection of Intrusionsamp;Malwareamp;VulnerablityAssessmentDIMVA 2004,Dortmund,Germany,2004.
[4]Dullien T,Rolles R.Graph-based comparison of executable objects(english version)[J].SSTIC,2005,5:1-3.
[5]曾鸣,赵荣彩,姚京松,等.基于特征提取的二进制代码比较技术[J].计算机工程与应用,2006,42(22):8-11.
[6]谢余强,曾颖,舒辉.改进的基于图的可执行文件比较算法[J].计算机工程与设计,2007,28(2):257-260.
[7]魏强,金然,王清贤.基于可信基点的结构化签名比较算法[J].计算机工程与设计,2007,28(24):5850-5853.
[8]傅建明,乔伟,高德斌.一种基于签名和属性的可执行文件比较[J].计算机研究与发展,2009,46(11):1868-1876.
[9]宋杨,张玉清.结构化比对算法研究及软件实现[J].中国科学院大学学报,2009,26(4):549-554.
[10]崔宝江,马丁,郝永乐,等.基于基本块签名和跳转关系的二进制文件比对技术[J].清华大学学报:自然科学版,2011(10):1351-1356.
[11]陈慧,郭涛,崔宝江,等.二进制文件相似性检测技术对比分析[C]//信息安全漏洞分析与风险评估大会,2011:79-84.
[12]王建新,杨凡,韩锋.二进制文件比对中的指令归并优化算法[J].计算机应用与软件,2013(12):40-42.
[13]刘春红,郭涛,崔宝江,等.二进制文件同源性检测的结构化相似度计算[J].北京邮电大学学报,2012,35(3):56-60.
[14]刘星,唐勇.恶意代码的函数调用图相似性分析[J].计算机工程与科学,2014,36(3):481-486.
[15]牟永敏,杨志嘉.基于函数调用路径的软件实现与设计一致性验证[J].中国科学:信息科学,2014,44(10):1290-1304.
[16]孙贺,吴礼发,洪征,等.基于函数调用图的二进制程序相似性分析[J].计算机工程与应用,2016,52(21):126-133.
XIAO Ruiqing1,LIU Shengli1,YAN Meng2,XIAO Da1,SUN Haobin1
1.State Key Laboratory of Mathematical Engineering and Advanced Computing,Zhengzhou 450001,China 2.Xi’an Newspaper Media Group,Xi’an 710002,China
Comparison technology of binary files based on hierarchical nodes.Computer Engineering and Applications,2017,53(21):144-150.
The existing methods of binary files comparison is mainly achieved by the comparison of structural directed graph,such as BinDiff,it has problems such as mismatch caused by structure similar and high time-consumption of analysis.A matching method based on node hierarchy and node value is proposed to solve this problem.By extracting the hierarchical and value information of the function node which in the function call graph,providing a node level estimation algorithm for nodes which hierarchical information is unclearly,it has matched nodes recursively in the end.Experiments show that this method avoids the mismatch caused by structural similarity,the time consumption is less than 1/2 of the time consumed by the structured matching tool BinDiff,and the reduction of matching nodes’number less than 15%.This method can effectively improve the cross-version similarity analysis efficiency of the embedded device firmware.
binary files comparison;hierarchical analysis;node value analysis;structural graphics
A
TP309
10.3778/j.issn.1002-8331.1612-0044
国家自然科学基金(No.61271252);国家重点研发计划(No.2016YFB0801505,No.2016YFB0801601)。
肖睿卿(1992—),男,硕士研究生,研究领域为信息安全,E-mail:Xiao_paper@126.com;刘胜利(1973—),男,博士,教授,研究领域为网络安全;颜猛(1973—),男,研究领域为网络安全;肖达(1981—),男,博士,副教授,研究领域为网络安全;孙豪彬(1988—),男,硕士研究生,助理工程师,研究领域为网络安全。
2016-12-05
2017-01-17
1002-8331(2017)21-0144-07
CNKI网络优先出版:2017-04-14,http://kns.cnki.net/kcms/detail/11.2127.TP.20170414.1850.040.html
