犹豫语言信息集成算法及其数据库选择应用
2017-11-28彭守镇林显宁吴桂明
彭守镇,林显宁,吴桂明
广东理工学院 信息工程系,广东 肇庆 526100
犹豫语言信息集成算法及其数据库选择应用
彭守镇,林显宁,吴桂明
广东理工学院 信息工程系,广东 肇庆 526100
针对犹豫模糊语言环境下的多属性群决策问题,建立了一种基于犹豫语言几何Bonferroni平均(HLGBM)算子的多属性群决策模型,该模型不仅充分考虑了每种属性的重要性,而且能够有效捕获属性间的内在联系。首先利用基于Archimedean T-范数和S-范数的犹豫语言运算法则,提出了一种新的HLGBM算子,并研究该算子的四种基本性质;其次,探讨了HLGBM算子的几类特殊形式,并提出了犹豫语言加权几何Bonferroni加权(HLWGBM)算子;最后基于HLWGBM算子构建了一种新的犹豫语言多属性群决策模型,并通过数据库选择实例验证决策模型是可行和有效的。
犹豫模糊语言集;Archimedean范数;几何Bonferroni平均;多属性群决策
1 引言
随着社会的快速发展,人类在认知问题时思维具有一定的局限性,再加上客观世界本身存在复杂性、模糊性和不确定性,导致在进行管理决策分析时,决策者常常不能给出精确的决策信息[1]。1965年Zadeh首次提出了模糊集的概念[2]。随后,Atanassov[3]针对模糊集的不足引入了直觉模糊集的概念,其利用隶属度、非隶属度以及犹豫度从三个方面精确地表达决策信息。针对专家在群决策问题中表现出犹豫不定和优柔寡断的情形,Torra[4]引入了犹豫模糊集的概念,其能够更为全面地表达决策信息。与区间模糊集不同,犹豫模糊集的隶属度是若干个实数值而不是区间值,这能够在处理群决策问题时更为有效地保证决策信息真实性[5]。
多属性群决策问题中一个重要课题是属性信息集成方式的构建[6-8]。在直觉模糊环境下,文献[9]定义了新的运算法则,并且建立了一系列直觉模糊信息集成算子方法。文献[10]将直觉模糊Bonferroni平均进行推广,引入了广义形式的直觉模糊加权Bonferroni平均和直觉模糊加权Bonferroni几何平均。Wei[11]将优先算子推广到犹豫模糊环境中,提出了一系列的犹豫模糊优先集成算子用以处理多准则决策问题。Jin等[12]针对文献[11]中算子的不足,提出了两个改进的犹豫模糊集成算子,同时证明其满足幂等性和有界性,最后构建了新的群决策方法。针对决策信息为区间直觉梯形模糊数的MAGDM问题,周晓辉和姚俭[13]提出了一种基于区间直觉梯形模糊几何加权Heronian平均算子和区间直觉模糊几何Heronian平均算子的决策方法。针对属性间存在优先关系的区间犹豫模糊多属性群决策问题,Jin等[14]基于信息集成算子构建了新的群决策模型。为了集成三角模糊数,刘金培等[15]提出了模糊Bonferroni平均算子和组合加权Bonferroni平均算子,同时研究了它们的一些性质。
分析发现,现有的大部分信息集成方法存在以下问题:(1)现有决策问题中决策者越来越偏好于运用语言变量表达定性决策信息;(2)在进行群决策过程中,决策者们提供的决策信息通常是不一致的。于是为了防止决策信息的丢失,需要保留所有的语言决策信息,因此犹豫模糊语言集[16]的概念被提出了;(3)几何Bonferroni平均[17]不仅能够处理复杂决策问题中属性信息之间存在的内在联系,还能够考虑到每种属性的重要性;(4)现有信息集成算子都是运用基于代数范数得到的,而代数范数只是Archimedean范数的一种运算形式[18],且Archimedean范数能够使得集成方法更加灵活。因此,有必要对犹豫语言环境下结合几何Bonferroni平均和Archimedean范数,深入研究考虑属性输入变量间存在联系的新算子形式。本文首先基于Archimedean范数定义了新的犹豫语言运算法则,然后结合几何Bonferroni平均提出了犹豫语言几何Bonferroni平均算子,并研究了算子的基本性质和几类常见的算子形式,最后基于提出犹豫语言加权几何Bonferroni平均算子构造了一种新的多属性群决策方法,并将其应用于实例中。
2 基础知识
本章首先介绍一些基础知识,包括几何Bonferroni平均、犹豫模糊语言集和Archimedean范数。为了讨论方便,令 N={1,2,…,n}。
2.1 几何Bonferroni平均
在信息集成过程中,几何Bonferroni平均不仅能够考虑输入属性信息间的内在联系,还能突出每种属性的重要程度。
定义1[11]对于一列非负实数ai(i=1,2,…,n),且参数 p,q>0,则几何Bonferroni平均(GBM)满足以下形式:

2.2 犹豫模糊语言集
令 S={s0,s1,…,s2τ}是一个离散语言集[19],其中 si为语言变量。语言集S需要满足的两个特征,即:(1)有序性:若 i≤j,则 si≤sj;(2)逆算子:neg(si)=s2τ-i。文献[19]基于离散语言集S引入了连续语言集={si|s0≤si≤s2τ,i∈[0,2τ]},其中 τ为一个充分大的正数。分析可知,语言变量间的计算是语言变量下标间的运算,则引入函数,使得同时存在函数I(⋅)的反函数 I-1(⋅):[0,1]→,满足对任意的 i∈[0,1],有I-1(i)=s2τi。
定义2[16]设S={s0,s1,…,s2τ}为一个给定的语言术语集,称定义在集合X上的犹豫模糊语言集(HFLS)为A={<x,hA(x)>|x∈X},其中 hA(x)记为犹豫模糊语言元(Hesitant Fuzzy Linguistic Element,HFLE),表示元素x属于集合A的可能语言隶属度集合,它是由S上几种不同的语言变量构成。
定义3[16]令h为一个HFLE,则称为HFLEh的得分函数。假设h1和h2为两个HFLE,当Δ(h1)>Δ(h2)时,那么 h1>h2;当 Δ(h1)=Δ(h2)时,那么h1=h2。
2.3 Archimedean范数
若二元函数T(x,y)满足单增、对乘性、结合律、存在单位元1、在定义域内连续,且对 ∀x∈(0,1),有T(x,x)<x,则称 T(x,y)为Archimedean T-范数。若二元函数S(x,y)满足单增、对乘性、结合律、存在单位元0、在定义域内连续,且有 S(x,x)>x,∀x∈(0,1),则称S(x,y)为 Archimedean S-范数[18]。
相关研究表明,严格Archimedean T-范数可由一个严格单调递减的加性算子 g:[0,1]→[0,+∞]表示为T(x,y)=g-1(g(x)+g(y)),其中 g(1)=0,g(0)=1。根据对偶原则,严格Archimedean S-范数可表示为S(x,y)=f-1(f(x)+f(y)),其中 f(t)=g(1-t),于是 f(t)严格单调递增,且 f(0)=0,f(1)=1[18]。
3 犹豫语言几何Bonferroni平均算子
本章首先运用Archimedean T-范数和S-范数在犹豫模糊语言环境下定义新的运算法则,然后基于提出的运算法则构建一种新的犹豫语言几何Bonferroni平均算子。
3.1 犹豫模糊语言运算法则
定义4设h,h1,h2为三个HFLE,定义运算如下:
(1)hc={ }
neg(γ)|γ ∈ h
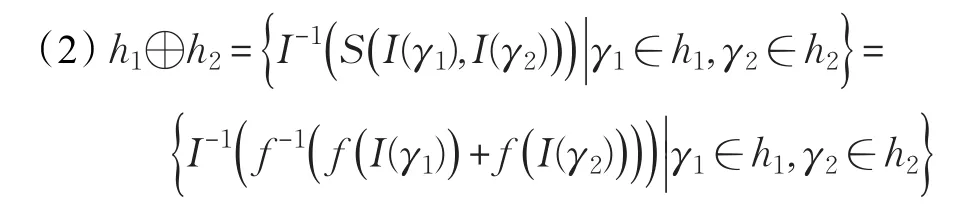

3.2 犹豫语言几何Bonferroni平均算子
由于决策者提供的属性信息通常以语言变量的形式给出,为了保持决策信息的全面性,将运用HFLE表示方案在属性指标下的决策信息。针对犹豫模糊语言环境下的多属性决策问题中需要将某一个方案在不同指标属性下的决策信息进行综合集结,并且能有效获取属性间的内在关系以及考虑每种属性的重要性,提出犹豫语言几何Bonferroni平均算子。
定义5令hi(i=1,2,…,n)为一列HFLE,且参数p,q>0,则犹豫语言几何Bonferroni平均(HLGBM)算子为:
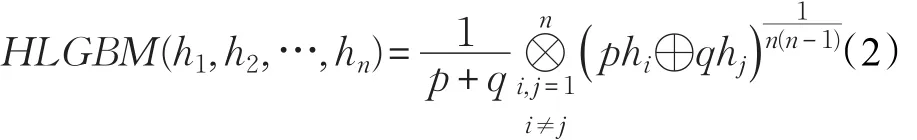
定理1 令hi(i=1,2,…,n)为一列HFLE,参数 p,q>0,则运用HLGBM算子得到的集成结果仍为HFLE,且
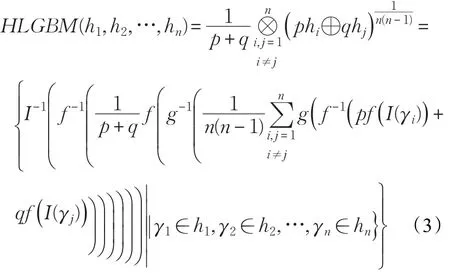
证明 首先证明公式(3)成立。对任意的HFLEhi和hj,运用定义4中的犹豫模糊语言运算法则,可得:


那么
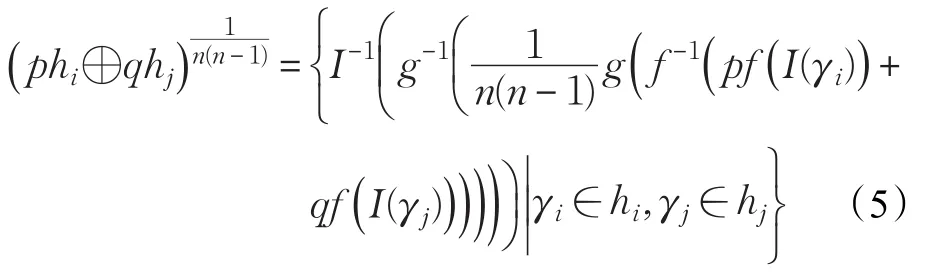
于是有:

因此,再依据定义4可得:

于是定理中的公式(3)成立。
现证明将一列HFLE通过HLGBM算子集成得到的结果还是HFLE。由2.3节可知g(t)和g-1(t)为严格单调递减函数,f(t)和 f-1(t)为严格单调递增函数,且g(1)=0,g(0)=1,f(0)=0,f(1)=1。
因为0≤I(γi)≤1,0≤I(γj)≤1,所以有:

于是

所以
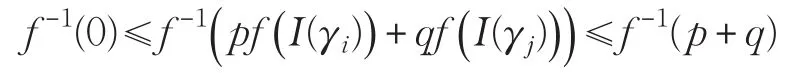
由于g(t)和g-1(t)为严格单调递减函数,因此
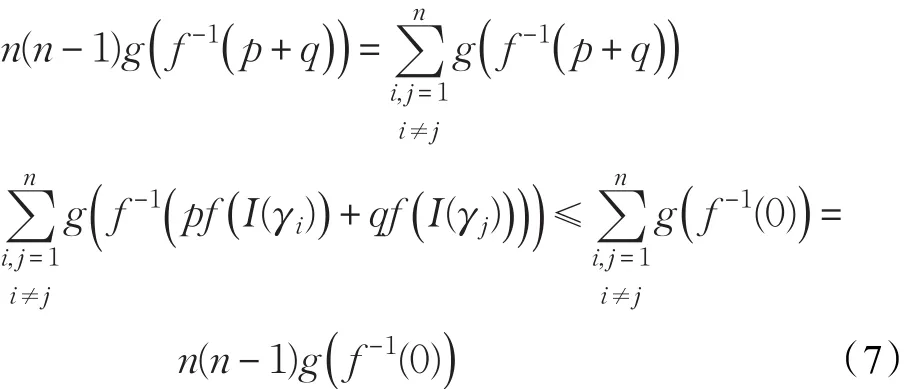
那么
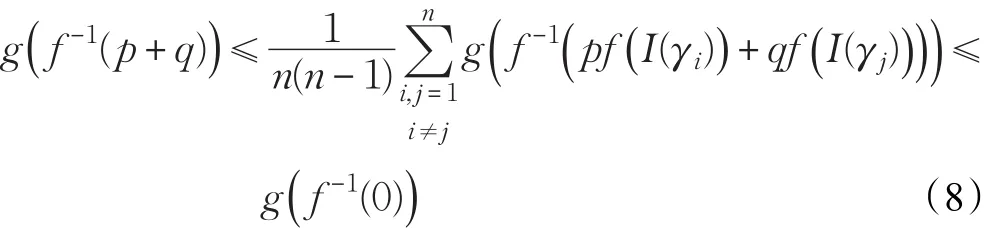
运用函数 g-1(⋅)对公式(8)进行作用,可得:

于是有:
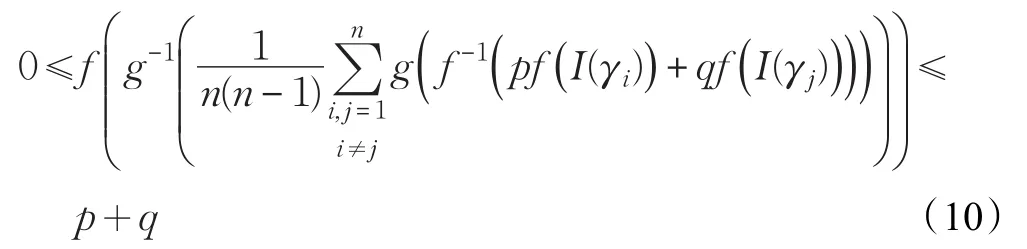
从而
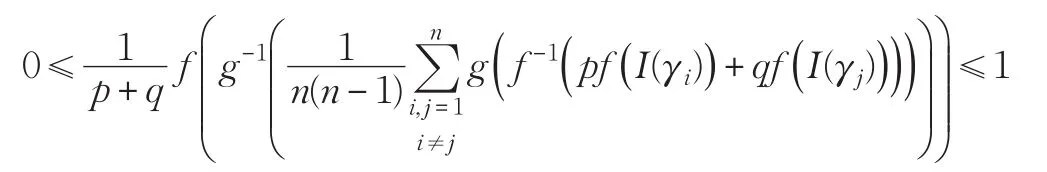
所以有:s0=I-1(0)≤
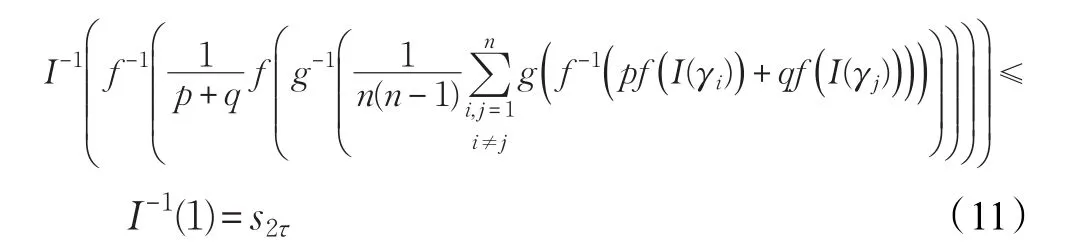
这表明HLGBM算子集成得到的结果仍是HFLE。于是
定理1得证。
4 HLGBM算子的基本性质及其常见算子形式
本章首先谈论HLGBM算子满足的一些基本性质,然后研究HLGBM算子的几种常见形式,最后提出HLGBM算子的加权形式。
4.1 HLGBM算子的基本性质
定理2(幂等性)设hi(i∈N)为一列HFLE,若对∀i∈N ,有 hi=h,那么
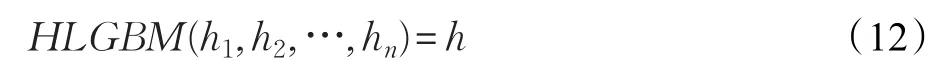
定理3(单调性)设 αi,βi(i∈N)为两组HFLE,若对∀i∈N ,有 αi≤βi,那么
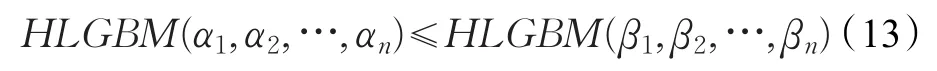
定理4(有界性) 设 hi(i∈N)为一组HFLE,若,那么

定理5(置换不变性)设hi(i∈N)是一组HFLE,若是 (h1,h2,…,hn)的一个任意置换,则有:

4.2 赋予g(t)不同的函数
(1)当 g(t)=-ln(t)时,有:


其中 νi=I(γi),i∈ N

4.3 参数 p,q取不同的实数
(1)当q→0时,可得:


(3)当 p=1且q→0时,可得:

(4)当 p=q=1时,可得:
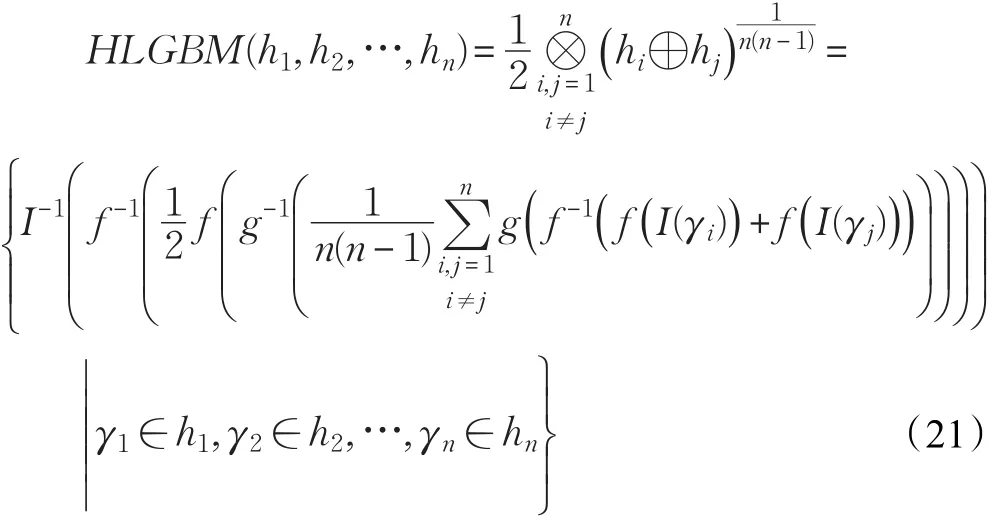
4.4 犹豫语言加权几何Bonferroni平均算子
针对现实决策问题中属性的重要性程度通常不相同,令hi(i∈N)为一组HFLE,其权重向量为w=(w1,w2,…,wn)T,且满足,参数 p,q>0,则称
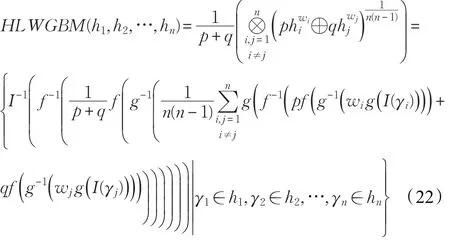
为犹豫语言加权几何Bonferroni平均(HLWGBM)算子。
5 基于HLWGBM算子的多属性群决策方法及案例分析
5.1 问题描述
考虑属性值为犹豫模糊语言信息的多属性群决策问题。假设 X={X1,X2,…,Xm}为一组备选方案,C={C1,C2,…,Cn}为属性指标集合,其权重向量为w=(w1,w2,…,wn)T且满足决策过程中决策者不仅要考虑到属性之间的联系,而且决策者提供的信息安全系统Xi在属性指标Cj下的决策信息需以语言变量的形式给出,从而,所有决策者提供的信息安全系统Xi相对于属性指标Cj的语言变量构成一个HFLEhij,最终备选方案集X在属性指标集C下的所有HFLE可以组成一个犹豫模糊语言决策矩阵H=(hij)m×n。
5.2 多属性群决策方法
在犹豫模糊语言环境下,利用本文提出的HLWGBM算子处理上述属性间存在相互联系的多属性群决策问题,详细步骤如下:
步骤1若Cj(j∈N)均为效益型属性,则决策矩阵不变;否则,对H=(hij)m×n进行如下标准化处理,得到标准犹豫模糊语言决策矩阵B=(βij)m×n:

步骤2运用HLWGBM算子:
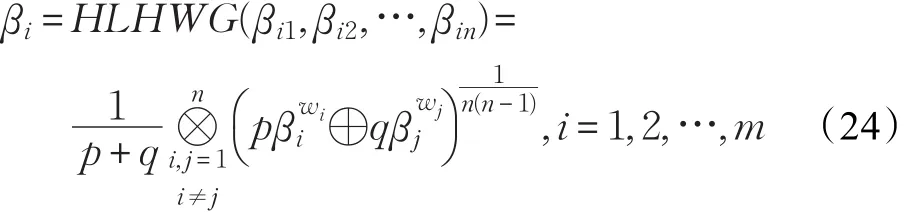
计算每种方案 Xl(i=1,2,…,m)的综合属性值 βi(i=1,2,…,m)。
步骤3依据定义3分别计算各备选方案综合属性值βi(i=1,2,…,m)的得分函数Δ(βi),并进行大小排序。
步骤4基于βi(i=1,2,…,m)的大小顺序对各备选方案进行优劣排序,并选择出综合性能最优的方案。
5.3 案例分析
某软件开发公司为了适应大数据环境下数据存储的海量需求,欲从市场上采购一套数据库。该公司采购部门根据自身需求在市场中挑选出四套符合条件的数据库Xi(i=1,2,3,4)以供选择。为了客观合理地选择出综合性能最优的数据库,采购招商部门邀请一组相关领域的专家学者对这四套数据库在如下四种指标下进行定性评估,即C1:存储量、C2:收益率、C3:使用寿命和C4:售后服务与技术,并且指标权重向量为w=(0.15,0.3,0.2,0.35)T。专家们依据自身的专业知识和经验技能,给出了每套数据库在各属性下的评估信息HFLE hij={γij∈ S={s0,s1,…,s8}},进而得到了表1所示的犹豫语言决策矩阵H=(hij)4×4。接下来将运用本文构建的数据库选择模型处理上述数据库选择问题,详细过程如下。
利用5.2节中建立的多属性群决策方法处理上述问题,具体过程如下:
步骤1由于四种属性指标下的属性值越大越好,即Ci(i=1,2,3,4)均为效益型,所以H不需标准化。


步骤3运用得分函数计算公式计算四套数据库的综合属性值hi(i=1,2,…,5)的得分函数为:

步骤4 因为 Θ(h3)>Θ(h1)>Θ(h2)>Θ(h4),所以这四套数据库的综合性能优劣排序为:
X3≻X1≻X2≻X4
于是综合性能最优的数据库为X3。
由上一节可知,在参数 p,q发生变化时会使得HLWGBM算子转化为不同的信息集成算子,这可能导致四套数据库的优劣排序稍有不同,从而出现不同的决策结果。因此,本文将对参数 p,q分别进行分析,探究参数变化对决策结果的影响。不失一般性,加性算子仍然取
(1)当q=0时研究参数 p对决策结果的影响。以参数p为自变量,以四套数据库综合属性值的得分函数值为因变量,可以得到如图1所示的变化趋势图。研究发现,当参数q=0时,随着参数 p的增加,四套数据库综合属性值的得分函数是逐渐递减的,且数据库的优劣排序会有所改变:当q=0,p∈[0,1.89]时,四套数据库的综合性能优劣排序为 X3≻X1≻X2≻X4;当 q=0,p∈[1.89,3.88]时,四套数据库的综合性能优劣排序为X3≻X1≻X4≻X2;当 q=0,p∈[3.88,10]时,四套数据库的综合性能优劣排序为X3≻X4≻X1≻X2。
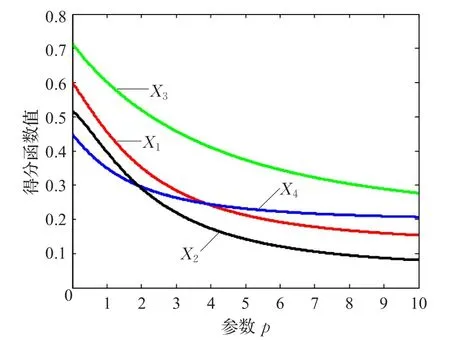
图1 四套数据库得分函数值随参数p的变化趋势
(2)当 p=0时研究参数q对决策结果的影响。以参数q为自变量,以四套数据库综合属性值的得分函数值为因变量,得到如图2的变化趋势图。由图2可知,当参数 p=0时,随着参数q的增加,四套数据库综合属性值的得分函数是逐渐递减的,且数据库的优劣排序会有所改变:当 p=0,q∈[0,0.1]时,四套数据库的综合性能优劣排序为X3≻X4≻X1≻X2;当 p=0,q∈[0.1,0.79]时,四套数据库的综合性能优劣排序为X3≻X1≻X4≻X2;当p=0,q∈[0.79,2.87]时,四套数据库的综合性能优劣排序为 X3≻X1≻X2≻X4;当 p=0,q∈[2.87,10]时,四套数据库的综合性能优劣排序为X3≻X2≻X1≻X4。

图2 四套数据库得分函数值随参数q的变化趋势
6 结束语
本文首先在犹豫模糊语言环境下利用Archimedean范数定义新的运算法则,并结合几何Bonferroni平均运算,提出了HLGBM算子,并探讨了算子的一些基本性质,研究了HLGBM算子的几种常用形式,引入了HLWGBM算子。最后,基于提出的HLWGBM算子构建了一种新的犹豫模糊语言多属性群决策方法,并将其应用于数据库的选择实验中。实验表明,提出的算子是可行有效的。在后续研究过程中,针对提出的犹豫模糊语言信息算子与现有算子间的大小和信息集成性能优劣的比较,将做进一步研究,同时将提出的决策方法应用于图像去噪、模式识别以及供应链等领域。
[1]王敬丰.C-POWGA算子及其在不确定多属性决策中的应用[J].计算机工程与应用,2015,51(9):57-61.
[2]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[3]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.
[4]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25(6):529-539.
[5]陈秀明,刘业政.多粒度犹豫模糊语言环境下未知权重的多属性群推荐方法[J].控制与决策,2016,31(9):1631-1637.
[6]Liu P D,He L,Yu X C.Generalized hybrid aggregation operators based on the 2-Dimension uncertain linguistic information for multiple attribute group decision making[J].Group Decision and Negotiation,2016,25(1):103-126.
[7]刘小弟,朱建军,李思峰.犹豫模糊信息下的双向投影决策方法[J].系统工程理论与实践,2014,34(10):2637-2644.
[8]Xu Z S.Intuitionistic fuzzy aggregation operators[J].IEEE Transactions on Fuzzy Systems,2007,15(6):1179-1187.
[9]Xu Z S,Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets[J].International Journal of General Systems,2006,35(4):417-433.
[10]Xia M M,Xu Z S,Zhu B.Generalized intuitionistic fuzzy Bonferroni means[J].International Journal of Intelligent Systems,2012,27(1):23-47.
[11]Wei G W.Hesitant fuzzy prioritized operators and their application to multiple attribute decision making[J].Knowledge-Based Systems,2012,31(7):176-182.
[12]Jin F F,Ni Z W,Chen H Y.Note on“Hesitant fuzzy prioritized operators and their application to multiple attribute decision making”[J].Knowledge-Based Systems,2016,96:115-119.
[13]周晓辉,姚俭.区间直觉梯形模糊几何Heronian平均算子及应用[J].计算机工程与应用,2016,52(9):39-43.
[14]Jin F F,Ni Z W,Chen H Y.Interval-valued hesitant fuzzy Einstein prioritized aggregation operators and their applications to multi-attribute group decision making[J].Soft Computing,2016,20(5):1863-1878.
[15]刘金培,林盛,陈华友.模糊Bonferroni平均算子及在多准则群决策中的应用[J].系统工程与电子技术,2012,34(1):115-119.
[16]Zhang Z M,Wu C.Hesitant fuzzy linguistic aggregation operators and their applications to multiple attribute group decision making[J].Journal of Intelligentamp;Fuzzy Systems,2014,26(5):2185-2202.
[17]Bonferroni C.Sulle medie multiple di potenze[J].Bolletino Matematica Italiana,1950,5:267-270.
[18]Xia M M,Xu Z S,Zhu B.Some issues on intuitionistic fuzzy aggregation operators based on Archimedean t-conorm and t-norm[J].Knowledge-Based Systems,2012,31:78-88.
[19]Zadeh L A.The concept of a linguistic variable and its application to approximate reasoning[J].Information Sciences,1975,8(2):99-249.
PENG Shouzhen,LIN Xianning,WU Guiming
Department of Information Engineering,Guang Dong Polytechnic College,Zhaoqing,Guangdong 526100,China
Hesitant linguistic information aggregation algorithm and its application to select database.Computer Engineering and Applications,2017,53(21):85-90.
For the Multi-Attribute Group Decision Making(MAGDM)problem under the hesitant fuzzy linguistic environment,based on Hesitant Linguistic Geometric Bonferroni Mean(HLGBM)operator,a novel MAGDM model is developed,which is considering the importance of each attribute and the interrelationships among them.Firstly,based on the hesitant linguistic operational laws with Archimedean T-norm and S-norm,this paper proposes the HLGBM operator,which is followed by the discussion of its desirable properties.Then,some special cases of the HLGBM operator are studied in detail and the hesitant linguistic weighted geometric Bonferroni mean(HLWGBM)operator is presented.Finally,a new model for MAGDM is investigated based on the HLWGBM operator,and applies the example for the selection of database to demonstrate the model’s practicality and effectiveness.
hesitant fuzzy linguistic set;Archimedean norm;geometric Bonferroni mean;multi-attribute group decision making
A
TP182
10.3778/j.issn.1002-8331.1705-0129
广东理工学院科技项目(No.GKJ2016006)。
彭守镇(1979—),男,讲师,主要研究方向为数据挖掘和决策算法;林显宁(1982—),男,讲师,主要研究方向为计算机技术和决策方法;吴桂明(1980—),男,讲师,主要研究方向为计算机网络安全和数据库应用。
2017-05-12
2017-06-29
1002-8331(2017)21-0085-06
