基于FPGA的进位存储大数乘法器的改进与实现

张晓楠 ，高献伟 ，，董秀则

1.西安电子科技大学 通信工程学院，西安 710071 2.北京电子科技学院 电子系，北京 100070

基于FPGA的进位存储大数乘法器的改进与实现

张晓楠1，高献伟1，2，董秀则2

1.西安电子科技大学 通信工程学院，西安 710071 2.北京电子科技学院 电子系，北京 100070

提出了一种基于FPGA的进位存储的大数乘法器的改进算法，该算法采用串并混合结构可以在一个时钟内完成多次迭代计算，减少了完成一次运算的时钟数，因此有效地提高了大数乘法器的速度。最后硬件结构设计在Altera Stratix II EP2S90F1508C3上实现，给出了192位、256位以及384位的乘法器性能分析，其中，192位可达到0.18 μs，256位达到0.27 μs，384位达到0.59 μs，速度上都提高了3.5倍左右。

大数乘法；串并混合结构；多次迭代；现场可编程门阵列

1 引言

乘法器是算术单元、数字信号处理器和其他算术运算的电路的重要功能单元。在很多领域都有重要应用，如密码体系、科学计算以及工程计算等方面。随着芯片集成度的不断提高和数据量的加大，特别是现代信息处理中对安全保密的高要求，对于乘法器，特别是大数乘法器的处理速度方面的要求也日益增大[1]。乘法器的处理过程大致相同，都是先生成部分积再相加。设计的关键是在于其运算速度的快慢。

为了加快大整数乘法，人们对大整数乘法的算法与实现进行了诸多研究。如参考文献[2]给出了利用Booth算法和Wallace Tree算法，通过减少部分积，并且把大数加法拆分为32位的加法来实现对于大数乘法的高速运算；文献[3]给出了一种43位浮点乘法器来进行高性能的乘法运算；文献[4]给出了一种高基（2H进制）的大数模乘硬件实现方法；文献[5]提出了一种并行行旁路（PRB）乘法器，通过对乘数进行重新编码并行输出部分积，从而使得乘法中的部分积减少，进而提高乘法速度。文献[6]和文献[7]的乘法器都是基于矩阵型乘法器的。本文提出了一种基于FPGA的进位存储的大数乘法器的改进算法，主要思路是在一个时钟完成多步迭代运算，降低完成一次运算的时钟数，通过仿真综合硬件面积和速率的综合考虑，得到最优的步数和速度。

2 进位存储乘法器结构

加法器是设计乘法器的的基础元件，加法器的应用主要是实现对部分积的相加，从而把乘法转换为加法运算。本文主要采用了进位存储加法器。

2.1 进位存储加法（CSA）

进位存储加法器[8]是一种简单的k个全加器全部并行的结构，没有任何的串行连接。如果对每位加法的进位保存下来，则两个或者两个以上的k位整数加法可以按位进行并行操作，得到两个整数，其中一个表示各个位的进位信息，另一个代表各个位的和信息。

假设要实现三个整数相加，输入分别为A,B,C，产生两个整数C'、S，得到2C'+S=A+B+C。其中和S的第 i位与进位 C′的第 i+1位可由 Si=Ai⊕Bi⊕Ci,Ci+1'=AiBi+AiCi+BiCi表示。即，一个进位存储加法器单元就是一个全加器单元。

例如：令 A=35,B=25,C=8，计算S和C′，A=35=（100011）2，B=25=（011001）2，C=8=（001000）2，所以S=（110010）2=50，C′=（001001）2=9，故 A+B+C=2C′+S=2×9+50=68。

2.2 进位存储乘法器设计

由于进位存储加法器相对于其他的加法器速度快很多，因此进位存储加法器应用到乘法器上应该会有效提高乘法器速度。进位存储乘法器的基本原理采用右移-加的乘法设计[9-10]。

算法 进位存储乘法器设计

输入 整数x，y(二者都是k位)。

输出 z=xy。

步骤1令 ps←0,pc←0,p←0。

步骤2对于i从0到k-1，重复执行

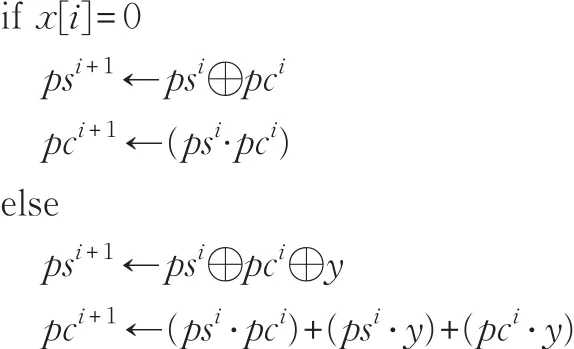
步骤3sum←ps+pc；

步骤4z←{sum,p}。

步骤5返回(z)。

算法的核心部分步骤2可表示为电路图图1形式。

从图1可看出该结构表示了进行一次迭代运算的过程，两个k位的数相乘需要经过k次的迭代运算，结果应是一个2k位的数，图1中的 p表示低k位，ps+pc共同表示了高k位，最终输出结果应为mult={ps+pc,p}。

图1 基于CSA的移位加乘法器的电路结构图

由于这种乘法器的实现形式属于每个时钟只进行了一次迭代运算，虽然在芯片面积上开销小，但速度欠缺，比如：完成一次192位的两个大数相乘运算大概需要浪费192个时钟，完成一次运算花费0.702 μs，大约1 s可以进行142万次乘法运算。

3 进位存储乘法器的改进及其硬件设计

一般来说，按照硬件实现的结构来分，大数相乘可以分为全串行结构、全并行结构和串并混合结构[11]。全并行结构一般要求在一个时钟周期内完成全部的计算过程，这样的实现方式虽然在时间上有很大提高，但代价是庞大的硬件开销，因此，一般只具有理论研究意义。全串行结构是在每个时钟周期只完成一次迭代计算，故需要很多个时钟周期，所以这种形式计算大数乘法虽然在硬件开销上相对于全并行结构少很多，但在时间上是不如全并行结构的计算速度。

综合考虑，最好的实现方案应当是：结合硬件开销和时间的最优匹配下的一种串并混合结构。

具体的实现原理：将进位存储乘法器算法（图1）中的一个时钟进行的一次迭代运算，共需要多个时钟才能完成一组大数乘法运算的这个过程，通过合理设计转化为一个时钟可以执行多步迭代运算，简单来说，就是将m位大数相乘需要m个时钟执行的m次迭代运，转化成一个时钟执行k步的迭代运算，即位数和步数之间的关系可由m=k×n+r表示。图2以192位，2步结构为例，说明了k步计算的核心结构，其中192-CSA结构代表了图1中的全加器和寄存器模块，图2中 p是由192 bit-CSA的输出依次从左向右顺序移入两位（此处是两步运算）。

4 大数乘法的硬件实现结果

实验的软件平台是基于QuartusII9.0，硬件平台选择ALTERA公司的1.2 v的StratixII系列的器件EP2S90F1508C3，该器件含有72 768个逻辑单元。

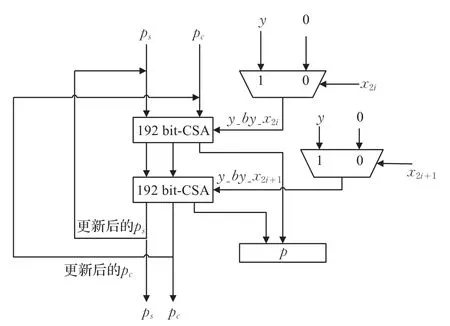
图2 192 bit的两步运算结构

实验证明，采用串并混合结构的大数乘法器，可以有效提高乘法运算的硬件实现速度。本文分别对192位、256位以及384位的大数乘法器进行了性能分析。表1给出了在不同步长k的条件下，192位的大数乘法运算的各项指标，即，所需要的时钟数（clk）、面积（LUTs）、器件的时钟频率 f（MHz）以及所耗费的时间t（μs）（进行一次运算所耗费的时间）。表1表明，随着步数k的增大，虽然占用逻辑资源LUTs数目在逐步增大，但计算一组大数乘法运算的时间总体上呈下降趋势。

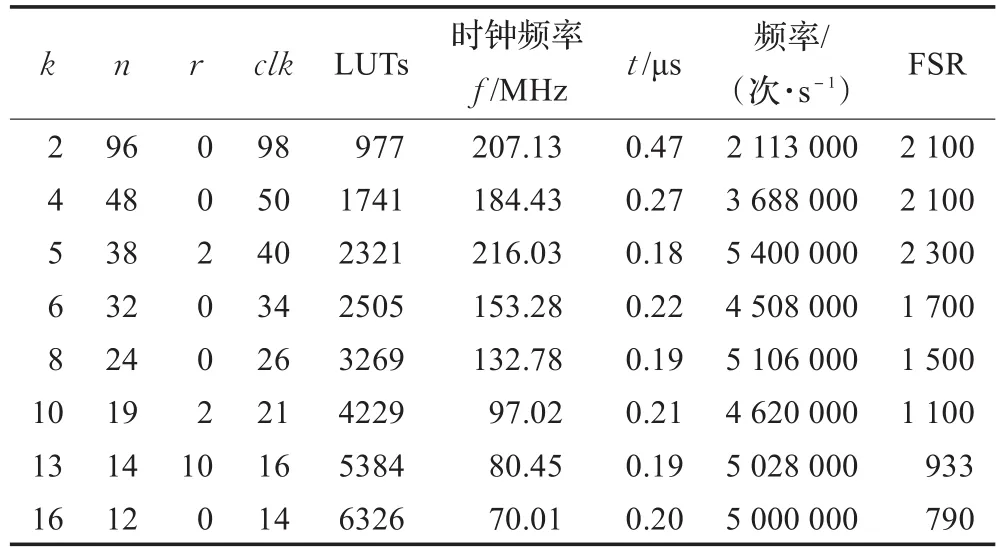
表1 m=192时，不同步长k下的乘法器性能分析

为了更清楚地分析该乘法器的性能，本文采用了一个新的性能指标——频率-面积比FSR（Frequency-Slices Ratio），其中

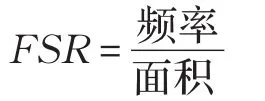
该指标不仅很好地诠释了完成一次乘法运算的次数、周期（频率）以及LUTs数目间的关系，而且通过该性能指标可以得到一个最优的占用逻辑资源与时间的折中方式，这有助于更好地衡量乘法器的性能。为了更加直观，特给出图3进行说明。从图3中可看出，FSR刚开始随着步数k的增大呈增长趋势，但当k继续增大，由于此时的面积开销大，故呈急速的下降状态，值得注意的是，图中的最高点应是时间与硬件资源开销的最优匹配，此时 k=5，频率/s/面积=2 326，频率 f=216.03 MHz，进行一次乘法运算所花费的时间为0.185 μs，1 s可进行大约5 400 750次运算。

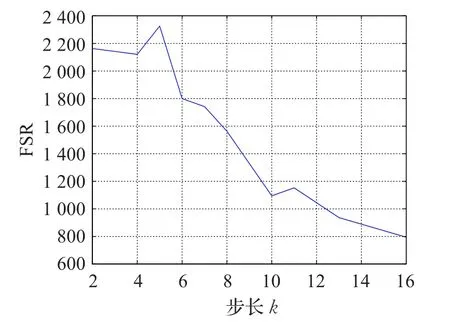
图3 步长与频率、LUTs之间的关系

同样，对位数m=256和m=384，进行了相同的性能分析，如表2和表3所示。

表2 m=256时，不同步长k下的乘法器性能分析

表3 m=384时，不同步长k下的乘法器性能分析

从表2可以看出，时间与硬件资源开销的最优匹配应为k=5时，此时频率 f=195.92 MHz，进行一次乘法运算所花费的时间为0.271 μs，1 s可进行大约3 841 568次运算。

通过表3可以得到，时间与硬件资源开销的最优匹配应为k=2时，此时频率 f=161.81 MHz，进行一次乘法运算所花费的时间为0.605 μs，1 s可进行大约165万次运算。

为了更好地分析改进的算法相对于未改进算法的优势，特别给出了表4进行了乘法器的性能比较。通过选择合适的步数得到了相应的速度，从表4中可以看出，在面积（LUTs）上，普通的CSA乘法器相对于改进后的CSA乘法器占用面积少，但是在速度上却低很多，为了更好说明改进后的乘法器的优势，表4中指标FSR很好地衡量了速度与面积之间的关系，这表明本文在提高速度的同时也兼顾了面积增大所带来的开销，例如：当m=192时，改进前的乘法器速度为1 425 000次/s，LUTs为597，改进后的乘法器速度为5 400 000次/s，LUTs为2 321，虽然改进后的LUTs增大很多，但从速度上看，提高了3.79倍多，指标FSR在改进前后差别不大，说明本文所改进的乘法器保证了速度与面积的合理平衡[12]。除此而外，表4也清楚地展示出这种串并混合结构的进位存储乘法器在速度上相对普通的提高很多，得到最终结论：192位乘法器速度提高了3.79倍多（5 400 750/1 425 103=3.79），256位乘法器速度提高了5.41倍多，384位乘法器速度提高了2.79倍多。

表4 全串行结构与串并混合结构的对比

5 总结

本文利用串并混合结构对进位存储乘法器做了改进，减少了完成一次运算的时钟数，从而有效地提高了乘法器的速度，此外，本文通过一个新的性能指标——FSR，很好地衡量了硬件资源与速率之间的关系，最后分别给出了192位、256位以及384位的硬件实现结果，通过FSR得到了最优的乘法器速度，相比普通的进位存储乘法器速度有很大改善。今后打算在素数域的模乘上应用此方法[13-14]，进一步改善模乘的速度，以便更好地应用于密码算法的硬件实现中[15]。

[1]杨军，余江，赵征鹏.基于FPGA密码技术的设计与应用[M].北京：电子工业出版社，2012.

[2]丁顺全，杨永福.一种快速大数乘法器的设计方法[J].红河学院校报，2009，7（2）：51-55.

[3]谷理想.一种高性能乘法器的设计与研究[D].江苏无锡：江南大学，2009.

[4]王金波，张文科.大数模乘硬件设计与FPGA高速实现[J].信息安全与通信保密，2005（7）：349-353.

[5]商丽卫，刘耀军.并行行旁路乘法器的设计与实现[J].微电子学与计算机，2012，29（8）：134-137.

[6]沈俊忠，肖涛，乔寓然，等.一种支持优化分块策略的矩阵乘加速器设计[J].计算机工程与科学，2016，38（9）：1748-1754.

[7]周磊涛，陶耀东，刘生，等.基于FPGA的Systolic乘法技术研究[J].计算机工程与科学，2015，37（9）：1632-1636.

[8]张荣花.素域上乘法器的FPGA设计与实现[D].西安：西安电子科技大学，2012.

[9]Deschamps J P，Imana J L，Sutter G D.Hardware implementation of finite-field arithmetic[M].[S.l.]：McGraw-Hill Inc，2009：66-74.

[10]Bessalah H，Messaoudi K，Issad M，et al.Left to right serial multiplier for large numbers on FPGA[C]//IEEE International Conference on Mechatronics，2009：288-293.

[11]高向强，冯春阳，闫鑫，等.一种面向64位 DSP处理器的可重构 ALU研究及设计[J].微电子学与计算机，2015（10）：1-6.

[12]Kang J Y，Gaudiot J L，Kang J Y，et al.A simple high-speed multiplier design[J].IEEE Transactions on Computers，2006，55（10）：1253-1258.

[13]廖望，万美琳.可扩展双域模乘器设计与研究[J].华中科技大学学报：自然科学版，2015，43（9）：51-54.

[14]Morales-Sandoval M，Diaz-Perez A.Scalable GF（p）montgomery multiplier based on a digit-digit computation approach[J].IET Computersamp;Digital Techniques，2016，10（3）：102-109.

[15]谢天艺，黄凯.素数域椭圆曲线密码加速器的VLSI实现[J].计算机工程与应用，2016，52（1）：89-94.

ZHANG Xiaonan1,GAO Xianwei1，2,DONG Xiuze2

1.School of Telecommunication Engineering,Xidian University,Xi’an 710071,China 2.Department of Electronics,Beijing Electronics Scienceamp;Technology Institute,Beijing 100070,China

Improvement and implementation of carry-save large numbers multiplication on FPGA.Computer Engineering and Applications,2017,53（21）：58-61.

This paper proposes an improved algorithm of carry-save large numbers multiplication on FPGA,which can complete multiple iterations of operation in a clock with a serial-parallel hybrid structure.To some extent,reducing clocks to complete a operation,the structure improves the speed of the large numbers multiplication effectively.Finally,the results of the implementation of this multiplier for several operands sizes（192 bit,256 bit,384 bit）on Altera Stratix II EP2S90F1508C3 show that the time of 192 bit is 0.185 microsecond,256 bit is 0.271 microsecond,and 384 bit is 0.595 microsecond.As a result,the paper’s design is about 3.5 times than the previous design in speed.

large numbers multiplication;serial-parallel hybrid structure;multiple iterations;Field Programmable Gate Array（FPGA）

A

TP312

10.3778/j.issn.1002-8331.1606-0358

北京市自然科学基金（No.4163076）；北京电子科技学院校内科研基金（No.2014TD1-DXZ）。

张晓楠（1992—），女，硕士，主要研究方向为各种密码算法的FPGA实现，E-mail：zhangxiaonan1010@163.com；高献伟（1974—），男，教授，主要研究领域为SOC与FPGA技术在通信中的应用等；董秀则（1975—），男，工程师，主要研究领域为SOC技术与信息安全技术。

2016-06-27

2016-09-05

1002-8331（2017）21-0058-04

CNKI网络优先出版：2016-12-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161221.0841.010.html