数学建模思想在经济学中的应用——以购房贷款问题为例

王熙 大连市第八中学

数学建模思想在经济学中的应用
——以购房贷款问题为例

王熙 大连市第八中学

经济学一向是与数学分割不开的，早在经济学发展的初期就开始应用数学理论思想研究经济学问题。其中，数学建模思想由于其适用性广、分析性强、准确性高等特点，在经济学中的应用尤为广泛。数学建模可以帮助经济学研究人员把复杂的问题简单化，将经济学的理论转化为数学模型，能够更直观地进行理论分析，使得经济学中收入与支出问题、国民收入问题、供给与需求问题等更容易加以探索，并从而利用该分析结果指导实际的经济活动。近几年房地产行业十分火热，因此探讨房贷按揭问题具有重要的研究意义。在本文中，笔者将从数学建模思想出发，浅谈数学建模思想在房贷按揭问题中的应用。

经济学 数学建模思想 房屋按揭

一、数学建模思想的概述

（一）数学建模思想的概念介绍及应用

当进行科学且客观地研究某类实际现象且通过严谨周密的话语来表达研究结果的方式，被我们称之为数学。数学建模思想属于数学研究中的实际应用性较强的思考方法，其通过运用数学的理论知识和函数图形，对问题加以抽象和简化确定出主要的函数参数、变量等条件，从而建立起某种关系并刻画出一定的数学模型。随着经济的发展，经济学问题变得更为复杂，而且还必须保证解决经济学问题时决策科学、定量分析、精确预测未来发展。在这种情况下导入数学建模思想是十分必要的，因此数学建模逐渐成为解决经济学问题的一种强有力的数学手段。

（二）数学建模塑造经济学模型的一般步骤

通过数学建模思想解决经济学问题的主要方法就是构建经济学模型。经过研究发现，建立经济学模型一般需要三个步骤：第一要对实际的经济学问题及其相关背景知识进行深入了解与分析，然后通过假设将所要研究的经济学问题加以抽象及形象化的方式确立未知变量和参数，并用数学理论知识和计算方法来明确变量及参数的关系，最后将实际的经济学问题数据与构建模型的理论数据进行比较，得出最终结果。

二、数学建模思想和经济学的有机结合——以购房贷款问题为例

（一）房贷按揭问题的可讨论性

随着房地产行业的兴起和中国“家”的观念，使得近年来购买房子的人数只增不降，而在这种情况下由于每个家庭或个人收入的不同，所能承担贷款的按揭数额也就不同。那么对于买房者而言，购房贷款数额的多少、选择何种购房贷款方案都是实实在在的经济问题。

（二）实际案例的分析

案例：某地居民决定利用贷款方式购买一套住房，借贷40万，并通过10年时间还完全部款项。现有等额本金还款法、等额本息还款法两种方式进行贷款。求：这两种不同的贷款方式每月所需还款金额、总共所支付的利息以及对比得出两种方案中的最优方案。

分析：先比较两种不同的贷款方式，第一种等额本息还款法是每月以相等的额度平均偿还贷款本息,直至期满还清,这种方案比较容易作出预算。第二种等额本金还款法是每期还给银行相等的本金,但客户每月的利息负担就会不同，从而致使所承担的利息应该是随本金逐期递减，这种方案较难作出预算。

两种方案通过简单的比较难以作出判断，因此这就需要我们分别构建两种不同还款方式的数学模型对问题进行分析。

（三）构建模型前的假设

在构建模型之前，需要增加除问题提供的已知条件外的假设及设定问题的前提条件，从而更加准确地构建模型。因此，针对房贷问题应增加几项假设和前提：还款人能够按时还款、居民借用贷款的利息在借款期间保持在6%不变、银行借款利息按照复利计息等。

（四）模型的建立与求解

建立模型离不开约定问题参数对应题设条件，其中，约定居民向银行贷款的本金为A；居民每月应缴纳款项为B；居民向银行还款的总额为C；居民承担的总利息D；银行贷款的月利率X、年利率Y；贷款期数m、总还款期数n；

等额本息还款法的模型建立及求解：

设：月均还款总额为E；ai（i=1～n）为居民在第i个月还款前所欠银行金额；bi（i=1～n）为居民在第i个月还款后所欠银行金额；

根据等额本息还款的计算法可知：

第1个月还款前所欠金额为：a1=A（1+X）

第1个月还款后所欠金额为：b1=a1-E=A（1+X）-E

第2个月还款前所欠金额为：a2=b1（1+X）=A（1+X）2-E（1+X）

第2个月还款后所欠金额为：b2=a2-E=A（1+x）-E（1+X）-E

同理类推可知：

到第n期还款后，居民所欠银行贷款全额还清，因此bn=0

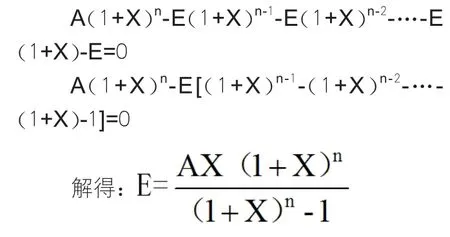
这就是居民每月平均还款总额

因此，居民总共的还款总额为：

总的利息负担为：

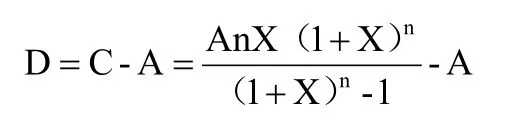
等额本金还款法的模型建立及求解：

根据上文所确定的参数假设，等额本金还款模型的建立可以直接利用上文参数，但与等额本息还款法不同的是：等额本金还款每期还款的本金相等，但是每期承担的利息不同，利息随本金的不断还款而不断递减。

设：居民第i个月应还款的金额为Xi（i=1～n）

根据等额本金还款的计算法可知：

第1个月应还款的金额为：E1=B+（A-B）X

第2个月应还款的金额为：E2=B+（A-2B）X

推理可知：

第n个月应还款的金额为：En=B+（A-nB）X

因此，居民总共的还款金额为：C’=E1+E2+…

总的利息负担为：

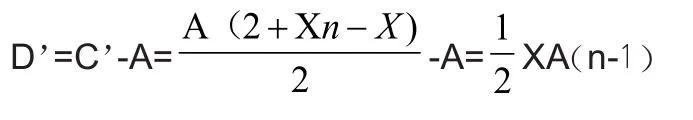
（五）对比数据结果选择方案

（1）等额本息还款法：

利用上文的模型代入已知条件可知：

总的还款期数n=120；贷款每月的利息率X=0.5%

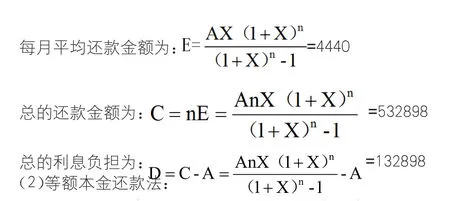
每月平均还款的金额：B=A÷n=3333，第一个月还款金额：5313

因此，居民总共的还款金额为：C’=E1+E2+…

（3）根据自身需求选择合适的购房贷款方案

对比两种方案还款方式可知，如果居民开头几期的还款能力较弱，那么首先推荐等额本息还款法，因为等额本息还款法每月还款金额是固定的且金额较等额本金还款法小。所以一般银行都是首推等额本息还款方案进行购房贷款，但是如果居民只考虑总的还款金额，那应该选择等额本金还款法，较等额本息还款法10年内少27796元。

三、结束语

想要深入有效的研究经济学问题，一定离不开构建好的数学模型。数学模型可以直观的将数据、走势以及数据之间的联系和差距反映给研究者，使研究者能够在面对问题时选择更好的方案，从而积极有效地解决问题。作为高中生来说，掌握数学基础知识不仅能够有效提高学习成绩，而且对以后从事经济学研究有很大的促进作用。

[1]石丽君.数学建模思想在高职金融数学课程上的应用实践①--以房贷按揭问题为例[J].科技创新导报.2015.

[2]张俊，毕公平，高慧朝，郝冰，罗林峰.房屋贷款中的数学建模问题[J].科技信息.2012.

[3]孙鲁予.住房商业性贷款中的数学模型研究[J].中小企业管理与科技旬刊 .2013