PM2.5与气象要素之间相关关系的回归分析
2017-11-27杜宇静李佩媛
杜宇静+李佩媛


摘 要 本文主要以2016年吉林市冬季和春季每日的PM2.5值与平均温度、风速和相对湿度的数据分别建立回归模型,并对模型进行多重共线性检验、自相关性检验、异方差性检验等,得到的结果为风速与PM2.5负相关,相对湿度与PM2.5正相关,并对冬季和春季两种情况作对比分析,最后根据得到的模型做预测分析,预测的结果较好。
关键词 PM2.5 回归分析 参数估计 显著性检验 预测
中图分类号:X513 文献标识码:A
0引言
PM2.5又称细颗粒物、细粒,对空气质量和能见度有非常大的影响,且能长时间悬浮于空气中。细颗粒物以自身直径小的优势,能进入呼吸道更深的部位,对人体健康的危害更大。很多人以为,PM2.5只是空气污染,其实它对整体的气候条件影响更糟糕,这就是我们看到蓝天白云的机会越来越少的原因。各种现象和研究说明,PM2.5同时影响着空气质量和天气气候;反而言之,在范圍较大的气候条件下,各气象因素也是可以影响空气中PM2.5的浓度的。近几年,人们已经对PM2.5的关注增大,对其环境污染方面的研究也逐渐增多。周兆媛研究京、津、冀三市空气污染与气象要素的相关关系。王琪等研究了北京地区PM2.5质量浓度分布及其气象条件影响关系,郑煜,蔺泽一等以哈尔滨冬季为对象进行相关性分析。
吉林市在我国东北地区,属于温带大陆性季风气候,四季分明。由于近年来全球气候变化加剧,吉林市的经济水平也在不断提高,吉林市的空气质量波动也在逐年增强,吉林市的污染情况在冬季尤为严重。本文分别研究了吉林市2016年冬季(2016.11.07-2017.02.02)和2017年春季(2017.02.03-2017.05.04)的空气污染中影响PM2.5浓度与气候因素的相关关系。
1模型的建立
本文选取吉林市2016年11月7日到2017年5月4日共计179天的数据作为原始数据。设因变量为PM2.5值(冬季:y1,春季:y2),自变量平均温度(冬季:x11,春季:x12), 风速(冬季:x21,春季:x22), 相对湿度(冬季:x31,春季:x32)。
1.1模型的建立
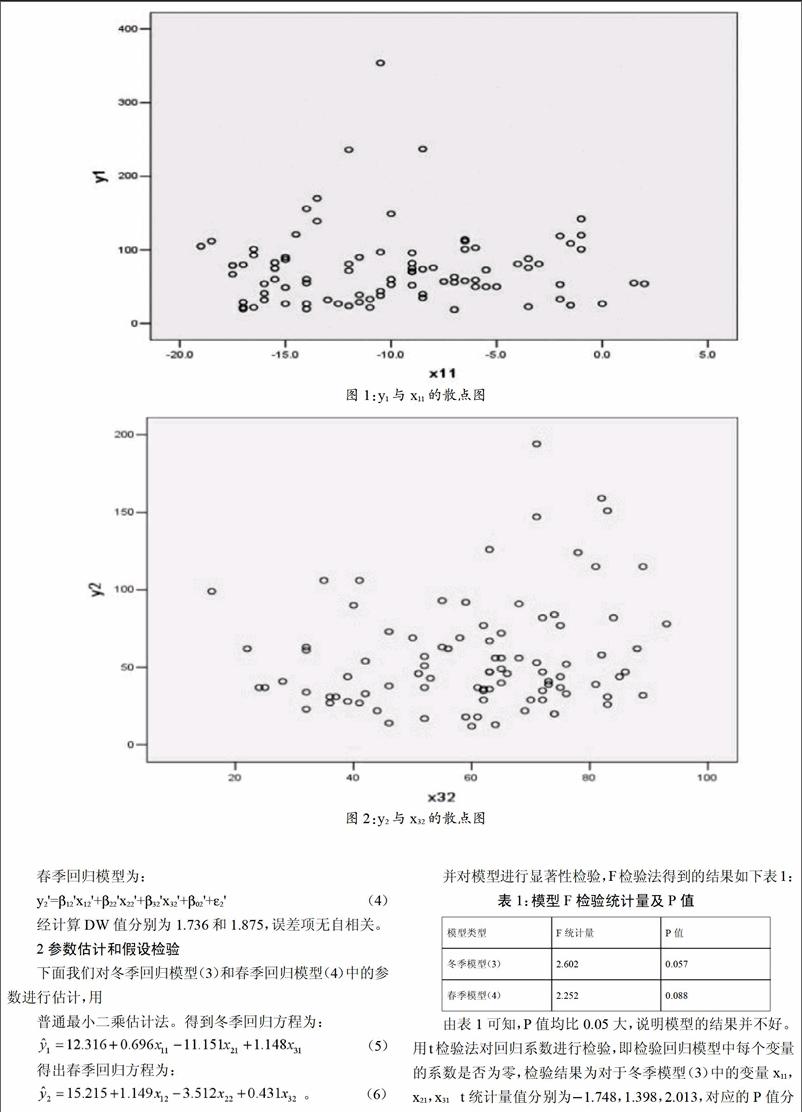
首先绘制散点图,然后判断因变量与自变量是否存在线性关系。下面图1和图2分别给出y1与x11、y2与x32散点图:
由散点图可以看出,平均温度和PM2.5值存在线性相关关系,同样风速和相对湿度与PM2.5值也存在线性相关关系。
多重共线性判定主要是检验自变量之间是否近似线性相关,这里用方差扩大因子法,计算共线性统计量VIF。冬季模型(1)中VIF值分别为1.021,1.035,1.055, 春季模型(2)中VIF值分别为1.938,1.266,1.8.13,VIF值均小于10,说明冬季模型和春季模型中的平均温度、风速和相对湿度之间不存在多重共线性。
建立模型时,某些因素会导致随机误差项产生不同方差,称为异方差性。利用等级相关系数检验法来判断回归模型的异方差性,此假设检验问题睥原假设为随机误差方差相等,通过计算得到冬季模型(1)中残差的绝对值与三个自变量之间的等级相关系数分别为0.114,0.072,-0.048,对应的P值分别为0.091,0.058,0.046。春季模型(2)中残差的绝对值与三个自变量之间的等级相关系数分别为0.000,-0.030,-0.005,对应的P值分别为0.099,0.051,0.035。因此可以判断不存在异方差性。
若模型中随机误差项之间不满足cov( i, j)=0,i≠j这个条件,则称随机误差项之间存在自相关现象。
经研究得出,随机误差项目有自相关性。另外,我们用DW检验法,对冬季回归模型(1)观测值的数目n=88,解释变量的数目k=4,查阅DW检验上下界表可知:dL=1.59,dU=1.73。计算得出DW值为1.019,满足0≤DW≤dL,可知误差项存在自相关。自相关系数 1=10.5DW=10.51.019=0.4905。
同理,可以判断春季模型(2)中的随机误差项之间存在自相关。我们可以用迭代法消除自相关性:
并对模型进行显著性检验,F检验法得到的结果如下表1:
由表1可知,P值均比0.05大,说明模型的结果并不好。用t检验法对回归系数进行检验,即检验回归模型中每个变量的系数是否为零,检验结果为对于冬季模型(3)中的变量x11,x21,x31 t统计量值分别为1.748,1.398,2.013,对应的P值分别为0.084,0.066,0.047,对于春季模型(4)的变量x12,x22,x32 t统计量值分别为1.579,1.301,1.765,对应的P值分别为0.118,0.197,0.081,变量x11、x12的P值相对较大,所以需要对模型进行改进。
将变量x11、x12从模型(5)(6)中去掉,分别得到改进的冬季的回归模型:
春季的回归模型:
经检验F值分别为3.772,3.014对应的P值分别为0.027,0.041,回归方程显著。
3预测和结论
预测是指在掌握现有信息基础上,依照一定的方法和规律对未来的事情进行预测,以预先了解事情发展的过程与结果。下面根据回归方程进行预测。经过计算2017年5月5日的预测值为52.1,而真实值为54,偏差为1.9,预测的结果相对较好,由预测结果可以看出建立的模型拟合度好。
从结果可以看出,吉林市冬季和春季PM2.5质量浓度有明显的季节区别,冬季较高,春季较低,这和吉林市冬季大范围取暖有必要的关系。此外,这两个季节PM2.5质量浓度的变化也受到了各季节不同的天气气候的影响。
吉林市冬季和春季PM2.5质量浓度的日变化与风速负相关,和相对湿度有正相关关系,这与郑煜等对哈尔滨冬季气象要素对空气质量指数的影响分析的结果相同。
两个季节中,平均温度、风速和相对湿度对PM2.5质量浓度的影响作用有所不同,风速的影响作用最大,而相对湿度的影响作用最小。综合作用下的效果:冬季模型和春季模型中,如果风速变大、相对湿度变小可以使PM2.5的质量浓度降低。
如果想通过改变一些气象因素的影响来降低PM2.5的质量浓度,可以采取以下个方法:减少降水量降低空气的相对湿度,相对湿度的降低可以使PM2.5质量浓度慢慢降低;可以采取一些倚靠大自然的方法来增加城市的空气流通情况,即风速对PM2.5质量浓度的影响,空气流通加快,城市的PM2.5质量浓度会降低;当然,也可以通过多个气象因素的互相作用来改变PM2.5的质量浓度。
参考文献
[1] 周兆媛,张时煌,高庆先,李文杰,赵凌美,冯永恒,徐明洁,施蕾蕾.京津冀地区气象要素对空气质量的影响及未来变化趋势分析[J].资源科学,2014(01).
[2] 王琪,孙巍,张新宇.北京地区PM_(2.5)质量浓度分布及其与气象条件影响关系分析[J].计算机与应用化学,2014(10):1193-1196.
[3] 郑煜,蔺泽一,张燕杰,张国财.哈尔滨冬季气象要素对空气质量指数的影响分析[J].黑龙江大学自然科学学报,2015(06):805-809.
[4] 何晓群,刘文卿.应用回归分析[M].中国人民大学出版社,2011.endprint
