完全多部图的符号罗马控制数
2017-11-27陈学刚
尹 凯,陈学刚
(华北电力大学数理学院,北京 102200)
完全多部图的符号罗马控制数
尹 凯,陈学刚
(华北电力大学数理学院,北京 102200)
设图G=(V,E)是一个简单无向图,若实值函数f:V→{-1,1,2}满足以下两个条件:(i)对于任意v∈V,均有∑u∈N[v]f(u)≥1成立;(ii)任意v∈V,若f(v)=-1,则存在一个与v相邻的顶点u∈V,满足f(u)=2,则称该函数为图G的符号罗马控制函数.定义图的符号罗马控制数为是图G的符号罗马控制函数}.通过对完全多部图中的顶点数进行分类,给出了当k≥3时,完全多部图K(n1,…,ni,…,nk)的符号罗马控制数的准确值.
完全多部图;符号罗马控制函数;符号罗马控制数
0 引言
文中所指的图均为简单无向图,文中符号和术语同文献[1].
设图G=(V,E)是一个简单无向图,V(G)和E(G)分别是图G的顶点集和边集.令顶点v的开邻域N(v)是指图G中所有与v相邻的点的集合.顶点v的闭邻域为N[v]=N(v)∪{v}.设S⊆V(G),若f是定义在图G顶点集上的任一实值函数,记作f(S)=∑v∈Sf(v).
完全多部图K(n1,…,ni,…,nk),其中k≥3.将其第i部顶点集合记作Vi={vi1,vi2,…,vink}.不妨设n1≤n2≤…≤nk.
若一个实值函数f:V→{0,1,2}满足条件:每一个使f(v)=0的顶点v至少相邻一个满足f(u)=2的顶点u,则称f(V)=Σv∈Vf(v)为图G的罗马控制函数.图的罗马控制数定义为是图G的罗马控制函数}.E.J.Cockayne等人在文献[2]中提出了上述概念,同时还研究了罗马控制数与图的其他控制数之间的关系以及相关性质,并给出了不同条件下罗马控制数的上下界.M.Chellali等人在文献[3]中又进一步对罗马控制数与其他控制数的关系进行了研究,并给出了罗马控制链.
图G=(V,E)为简单图,若实值函数f:V→{-1,1,2}满足以下两个条件:(i)对于任意v∈V,均有∑u∈N[v]f(u)≥1成立;(ii)任意v∈V,若f(v)=-1,则存在一个与v相邻的顶点u∈V,满足f(u)=2,则称该函数为图G的符号罗马控制函数.图G的符号罗马控制数定义为是图G的符号罗马控制函数}.若符号罗马控制函数f满足γSR(G)=∑v∈Vf(v),则称函数f为图G的γSR(G)-函数.Ahangar等人在文献[4]中提出了上述概念,并在文献[4-5]中给出不同条件下图G符号罗马控制数的上下界以及相关的临界图的刻画.S.M.Sheikholeslami等人在文献[6]中对符号罗马控制数已有的界进行了改进,得到了更好的上下界,并对不同条件下有向图符号罗马控制数的上下界进行了研究.文献[7-10]中还对其他控制参数进行了研究.
本文主要研究其中当k≥3时,完全多部图K(n1,…,ni,…,nk)的符号罗马控制数,并给出了完全多部图符号罗马控制数的准确值.文中为了证明方便,用G表示k≥3时的完全多部图K(n1,…,ni,…,nk),文中所指的均为k≥3的完全多部图.
1 完全多部图符号罗马控制数的值及证明
若函数f为完全多部图K(n1,…,ni,…,nk)时的一个γSR(G)-函数,令mi=f(Vi),其中
任意S⊆V(G),不妨设S={v1,…,vi,…,vk}.定义函数gi:S→{-1,1,2}如下:
(1)若k为奇数且k≥3,令g1(v1)=2,g1(v2)=-1,g1(v3)=-1,
(3)若k为偶数且k≥6,令g3(v1)=2,g3(v2)=-1,g3(v3)=-1,g3(v4)=2,g3(v5)=-1,
(4)若k∈{1,3},令g4(v1)=1,
(5)若k为奇数且k≥5,令g5(v1)=2,g5(v2)=-1,g5(v3)=-1,g5(v4)=2,g5(v5)=-1,
(6)若k为偶数,令g6(v1)=2,g6(v2)=-1,
(7)若k=2,令g7(v1)=1,g7(v2)=1.
(9)若k为奇数且k≥3,令g9(v1)=1,g9(v2)=1,g9(v3)=1,
(10)若k为奇数,令g10(v1)=-1,
(11)若k为奇数且k≥7,令g11(v1)=g11(v2)=2,g11(vi)=-1,其中3≤i≤7,
(12)若k为偶数且k≥4,g12(v1)=2,g12(vi)=-1,其中2≤i≤4,
(13)若k为偶数,令g13(v1)=g13(v2)=-1,
(14)若k为奇数且k≥3,令g14(vi)=-1,其中1≤i≤3,
其中4≤i≤k.
函数f={f1,f2,…,fk}表示对完全多部图K(n1,…,ni,…,nk)的第i部顶点集合采用函数 fi.
引理1:设f为完全多部图G=K(n1,…,ni,…,nk)的一个γSR(G)-函数,若对任意i∈{1,2,…,k},均有Vf-1∩Vi≠Ø,则γSR(G)≥3.
证明:对于任意1≤i≤k,有Vf-1∩Vi≠Ø.不失一般性,设f(v11)=f(v21)=…=f(vk1)=-1,

故(k-1)(m1+m2+m3+…+mk)≥2k.
由于γSR(G)=m1+m2+m3+…+mk,
引理2:设f为完全多部图G=K(n1,…,ni,…,nk)的一个γSR(G)-函数,若存在i∈ {1,2,…,k},满足
即任意f(vij)≥1,其中1≤j≤ni,则得证.
定理1:当n1=1时,完全多部图K(n1,…,ni,…,nk),其中k≥3,满足:
(1)γSR(K(n1,…,ni,…,nk))=2,其中n1=1;n2≥2.
(2)γSR(K(n1,…,ni,…,nk))=1,其中n1=…=nl=1;nk-1≥3.

证明:(1)设f为完全多部图G的一个γSR(G)-函数,若i∈{1,2,…,k},均有Vi≠Ø,由引理1得γSR(G)≥3.若i∈{2,…,k},均有则由引理2可得γSR(G)≥3>2.不妨设其中i=2,…,k.对于2≤i≤k,不失一般性,令f(v21)=f(v31)=…=f(vk1)=-1.因为f(N[vi1])≥1,所以:
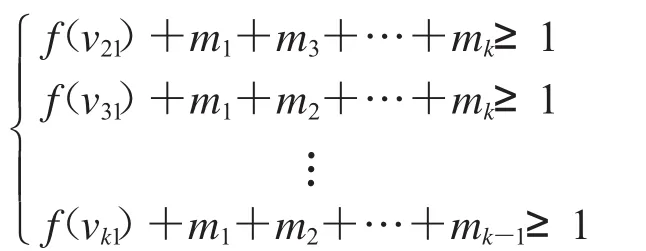
故(k-2)(m1+m2+m3+…+mk)≥2(k-1).
又因为γSR(G)=m1+m2+m3+…+mk,所以
另一方面,按如下方式定义f={f1,f2,…,fk}:其中2≤i≤k.易证该函数为完全多部图的符号罗马控制函数.故γSR(G)≤2.
(2)设f为完全多部图G的一个γSR(G)-函数,由定义知γSR(G)=f(N[v11])≥1.
另一方面:按如下方式定义f={f1,f2,…,fk}:
当l为奇数,且l≥3时:

易证该函数为完全多部图的符号罗马控制函数,所以γSR(G)≤1.综上,γSR(G)=1.
(3)设f为完全多部图G的一个γSR(G)-函数,
他撑开一把伞,把愁眉不展的母亲从医院接回来。母亲告诉他,罗素青的后事还没办,家里已经闹得不可开交。她写了遗嘱,出人意外地把遗产全部给了照顾她两年的保姆,没有给她的亲属留一分钱。她的亲人是她带大的一个侄子和两个侄女,现在他们愤怒了,不接受这个事实。
Vk,则f(N[vk1])≤-1,矛盾.因此
另一方面,按如下方式定义f={f1,f2,…,fk}:
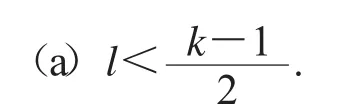
令fi=g8,其中1≤i≤l;fi=g13,其中l+1≤i≤2l;f2l+1=g7;

令fi=g8,其中1≤i≤l;fi=g13,其中l+1≤i≤2l-1;f2l=g2;

易证该函数为完全多部图的符号罗马控制函数,所以γSR(G)≤2.
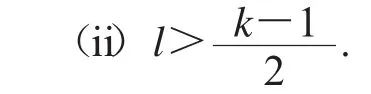
由定义γSR(G)=f(N[v11])≥1.
另一方面,按如下方式定义f={f1,f2,…,fk}:(a)k-l=1.
当l为奇数且l≥3时:

当l为偶数时:
若nk为奇数,令f1=f2=g8;
若nk为偶数,令f1=g8;f2=g4
(b)k-l>1.
当l为奇数且2l-k+1为奇数时:
令fi=g8,其中1≤i≤k-l;其
当l为奇数且2l-k+1为偶数时:
令fi=g8,其中1≤i≤k-l-1;fk-l=fk-l+1=g4;i≤l;fi=g13,其中l+1≤i≤k-1;
当l为偶数且2l-k+1为奇数时:
令fi=g8,其中1≤i≤k-l;其中l+1≤i≤k-1;
当l为偶数且2l-k+1为偶数时:
令fi=g8,其中1≤i≤k-l-1;fk-l=fk-l+1=g4;i≤l;fi=g13,其中l+1≤i≤k-1;
易验证上述情况中函数f均为该完全多部图G的符号罗马控制函数,因此γSR(G)≤1.
综上,γSR(G)=1.
(4)的证明由(3)的证明类似可得.
定理2:当n1=2时,完全多部图K(n1,…,ni,…,nk),其中k≥3,满足:
(1)γSR(K(n1,…,ni,…,nk))=2,其中n1=…=nl=2;存在ni,nj,满足ni≥3,nj≥3且ni≠4,nj≠4.
(2)γSR(K(n1,…,ni,…,nk))=3,其中n1=n2=…=nk-2=2;nk-1=3;nk=4.
(3)γSR(K(n1,…,ni,…,nk))=3,其中n1=…=nk-2=2;nk-1=4;nk=5,k≥4.
(4)γSR(K(n1,…,ni,…,nk))=2,其中n1=…=nk-2=2;nk-1=4;nk≥6,k≥4.
(5)γSR(K(n1,…,ni,…,nk))=2,其中n1=…=nl=2,l≥2;nl+1=…=nk-1=4,k-l≥3;nk≥5.
(6)γSR(K(n1,…,ni,…,nk))=3,其中n1=2;n2=…=nk-1=4;nk≥4.
(7)γSR(K(n1,…,ni,…,nk))=3,其中n1=n2=…=nk-1=2;nk≥2.
证明:
(1)设f为完全多部图G的一个γSR(G)-函数,若i∈{1,2,…,k},均有Vf-1∩Vi≠Ø,则由引理1可得γSR(G)≥3>2.若存在i∈{1,2,…,k},满足Vf-1∩Vi=Ø,则由引理2可得γSR(G)≥ni≥2.故γSR(G)≥2.
另一方面,按如下方式定义f={f1,f2,…,fk}:
令f1=g7;fi=g2,其中
易验证该函数为图G的符号罗马控制函数,所以γSR(G)≤2.
故γSR(G)=2.
(2)设f为完全多部图G的一个γSR(G)-函数,若i∈{1,2,…,k},均有则由引理1可得γSR(G)≥3.若则由引理2知γSR(G)≥3.若存在i∈{1,2,…,l},满足显然γSR(G)≥3.不妨设Vk=Ø且其中i=1,2,…,l.若存在i∈{1,2,…,l},满足不妨设则f(v11)=f(v12)=1.令显然γSR(G)≥3,故设又因为所以mk=f(Vk)=-1.同理可得mk-1=0.显然i∈ {1,2,…,k-2}时,mi为偶数,故m为偶数.
由定义γSR(G)=f(N[v11])+f(v12)≥2.若等号成立,则f(N[v11])=1,故m+mk-1+mk=0,m=1,与m为偶数矛盾.所以γSR(G)≥3.
另一方面,按如下方式定义f={f1,f2,…,fk}:
令f1=g6;fi=g2,其中2≤i≤k-2;fk-1=g4;fk=g6.易得f为图G的符号罗马控制函数,所以γSR(G)≤3.
故γSR(G)=3.
(3)类似于(2)的证明可得γSR(G)≥3.
另一方面,按如下方式定义f={f1,f2,…,fk}:
令f1=g6;fi=g2,其中2≤i≤k-2;fk-1=g6;fk=g5.易验证该函数为图G的符号罗马控制函数,故γSR(G)≤3.故γSR(G)=3.
(4)设f为完全多部图G的一个γSR(G)-函数,若任意i∈{1,2,…,k},有≤1成立,则由引理2可知γSR(G)≥2.若i∈{1,2,…,k},均有则由引理1可得γSR(G)≥3>2.
因此γSR(G)≥2.
另一方面,按如下方式定义f={f1,f2,…,fk}:
令f1=f2=g7;fi=g2,其中3≤i≤k-2;fk-1=g12;易验证该函数为图G的符号罗马控制函数,故γSR(G)≤2.
故γSR(G)=2.
(5)类似于(4)的证明可得γSR(G)≥2.
另一方面,按如下方式定义f={f1,f2,…,fk}:
令f1=f2=g7;fi=g2,其中3≤i≤l;fl+1=fl+2=g12;fi=g2,其中l+3≤i≤k-1;
易证该函数为图G的符号罗马控制函数,故γSR(G)≤2.
因此γSR(G)=2.
(6)设f为完全多部图G的一个γSR(G)-函数,若i∈{1,2,…,k},均有则由引理1可得γSR(G)≥3.若存在i∈{2,…,k},满足则由引理2得γSR(G)≥3.不妨设其中i=2,…,k.若易知γSR(G)≥3.若则f(v11)=f(v12)=1.对于i∈{2,…,k},不失一般性,令f(v21)=…=f(vk1)=-1,分以下情况讨论:

由于m1=2,且由定理2(2)中说明可知m2=m3=-1,故
由上述3种情况可得γSR(G)≥3.
故γSR(G)=3.
另一方面:按如下方式定义f={f1,f2,…,fk}:
令f1=f2=g6;fi=g2,其中3≤i≤k-1;易验证该函数为图G的符号罗马控制函数,故γSR(G)≤3.
综上,γSR(G)=3.
(7)设f为完全多部图G的一个γSR(G)-函数,
由情况1和情况2得γSR(G)≥3.
另一方面,按如下方式定义f={f1,f2,…,fk}:,易验证该函数为图G的符号罗马控制函数,所以γSR(G)≤3.
综上,γSR(G)=3.
证明:(1)若K(n1,n2,n3)=K(3,3,4),设f为完全多部图G的一个γSR(G)-函数,分以下情况讨论:
情况1:任意i∈{1,2,3},均有Vf-1∩Vi≠Ø.
由引理1可知γSR(G)≥3.若等号成立,可得m1+m2=m2+m3=m1+m3=2,即m1=m2=m3=1.不失一般性,设f(v11)=f(v21)=f(v31)=-1,则f(v12)=f(v13)=f(v22)=f(v23)=1,矛盾.故γSR(G)≥4.
另一方面:定义函数f={f1,f2,f3}:
令f1=g8;f2=g8;f3=g2.易证该函数为完全多部图的符号罗马控制函数,所以γSR(G)≤f(V)=g8(V1)+g8(V2)+g2(V3)=2+2+0=4.
故γSR(G)=4.
(2)若K(n1,n2,…,nk)≇K(3,3,4),设f为完全多部图G的一个γSR(G)-函数,若i∈{1,2,…,k},均有则由引理1可得γSR(G)≥3.若存在i∈{1,2,…,k},满足则由引理2可得γSR(G)≥ni≥3.故γSR(G)≥3.
另一方面,按照如下方式定义f={f1,f2,…,fk}:
①存在i∈{1,2,…,k},满足ni=4.
(i)n1=…=nl=3,其中l≥1.
令f1=g4;fi=g1,其中2≤i≤l


②任意i∈{1,2,…,k},均有ni≠4.
(i)n1=3,n2≥5.

(ii)n1=…=ni=…=nl=3,l≥2.

(iii)n1≥5.

易证上述情况下f均为完全多部图的符号罗马控制函数,故γSR(G)≤3.
综上,γSR(G)=3.
[1]BONDY J A,MURTY V S R.Graph theory with applications[M].Amsterdam:Elsevier,1976.
[2]COCKAYNE E J,DREYERJR P A,HEDETNIEMI S M,et al.Roman domination in graphs[J].Discrete Math,2004,278(1/2/3):11-22.
[3]CHELLALI M,HAYNES T W,HEDETNIEMI S M,et al.A Roman domination chain[J].Graphs Combin,2016,32(1):79-92.
[4]AHANGAR H A,HENNING M A,LWENSTEIN C,et al.Signed Roman domination in graphs[J].J Comb Optim,2013,308(4):2313-2318.
[5]AHANGAR H A,HENNING M A,LWENSTEIN C,et al.Signed Roman domination in graphs[J].J Comb Optim,2014,27(2):241-255.
[6]SHEIKHOLESLAMI S M,VOLKMANN L.Signed Roman domination in digraphs[J].J Comb Optim,2015,30(3):456-467.
[7]HENNING M A,VOLKMAN L.Signed Roman k-domination in graphs[J].Graphs Combin,2016,32(1):175-190.
[8]张立贤.图的参数控制研究[D].浙江:浙江师范大学,2015.
[9]张立贤,吕新中.图的逆罗马控制数[J].兰州文理学院学报(自然科学版),2015,29(1):5-11.
[10]曹惠萍.若干图类的全符号控制数的研究[D].大连:大连海事大学,2016.
Signed Roman Domination of Multi-Partite Graph
YIN Kai,CHEN Xuegang
(Institute of Mathematics and Physics,North China of Electric Power University,Beijing,102200)
A signed Roman domination function,of a simple undirected graph G=(V,E)is a function f:V→{-1,1,2}satisfying the conditions that(i)∑u∈N[v]f(u)≥1 for any v∈V,and(ii)every vertex v for which f(v)=-1 is adjacent to a vertex u for which f(u)=2.The signed roman domination number of G isis the signed roman domination of G}.In this paper,we compute the exact values of the signed roman domination numbers of complete multi-partite graph when k>=3,through classification the vertex of G.
complete multi-partite graph;signed roman domination function;signed roman domination number.
1001-4217(2017)04-0025-10
2017-02-26
尹凯(1992—),女,山西晋中,硕士研究生,研究方向:图论与组合优化.E-mail:huadianyinkai@163.com
中央高校基本科研业务费专项资金资助(2016MS66)
O 157.5
A
