一类分数阶微分方程边值问题的Lyapunov-type不等式研究
2017-11-27武忠文马德香
武忠文,马德香
(华北电力大学数理学院,北京,102206)
一类分数阶微分方程边值问题的Lyapunov-type不等式研究
武忠文,马德香
(华北电力大学数理学院,北京,102206)
一类包含 Caputo分数阶导数的边值条件情况下的 Caputo分数阶微分方程Lyapunov-type不等式被求出.首先,由Caputo分数阶导数的基本概念,把分数阶微分方程转化为积分方程,根据边值条件,求解出相应的格林函数.为了方便研究格林函数性质,我们从中提取出函数F(t,s).运用求导的方法,研究函数F(t,s)的性质,得到函数在整个区间的上下界.最后,在应用方面,对于一类分数阶微分方程特征值问题,求解了其特征值的存在区间;对于一类Mittag-Leffler函数,得到其零解不存在的区间.
分数阶微分方程;Lyapunov-type不等式;格林函数;Mittag-Leffler函数
0 引言
考虑下面边值问题
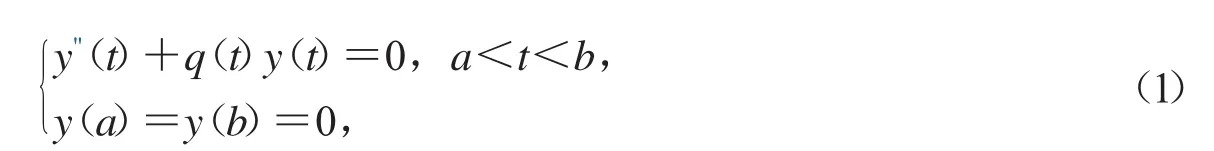
q(t)是一个实连续函数.如果式(1)存在非奇异解,则

文献[1]中得到了Lyapunov不等式(2).
文献[2]中,Ferreira研究了一类Caputo分数阶边值问题的Lyapunov型不等式:
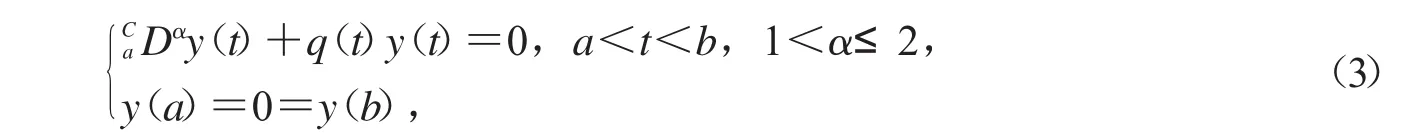
q(t)是一个实连续函数.如果式(3)存在非奇异解,则
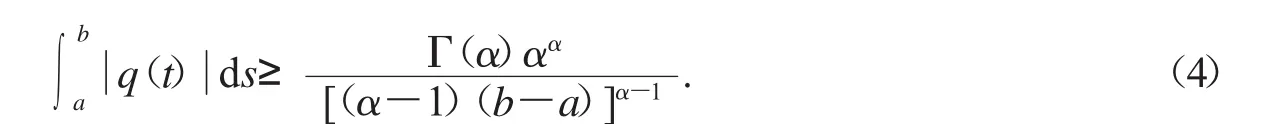
显然,令α=2,由式(4)推导出式(2).
文献[3]中,D.O’Regan和B.Samet研究了一类Riemann-Liouville分数阶边值问题的Lyapunov型不等式:
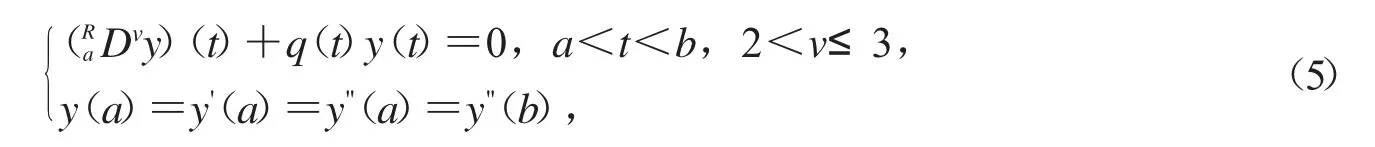
如果式(5)存在非奇异解,则
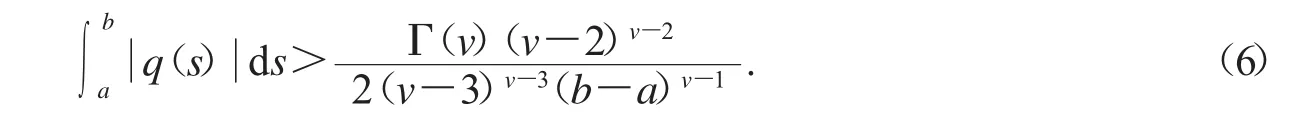
文献[4]中,Jleli和Samet研究了一类Riemann-Liouville分数阶边值问题的Lyapunov型不等式:
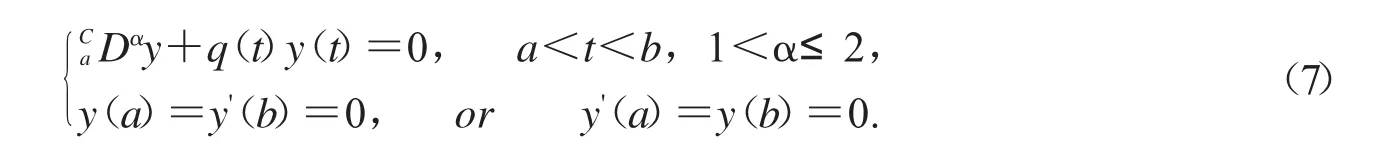
如果式(7)存在非奇异解,则
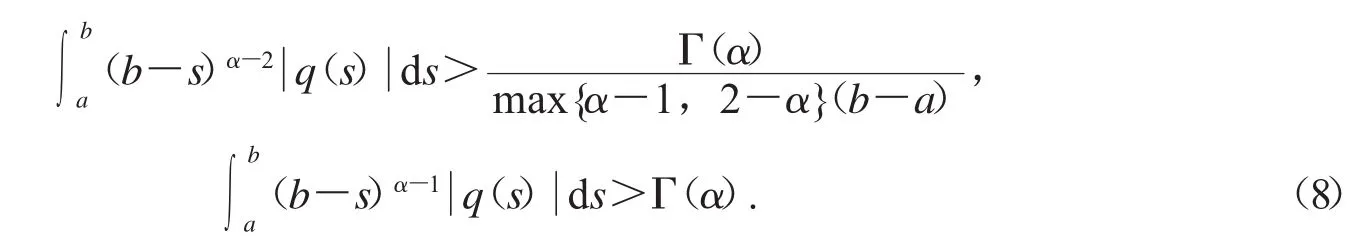
文献[5]中,Ji Rong和Chuanzhi Bai研究了一类Caputo分数阶边值问题的Lyapunov型不等式:
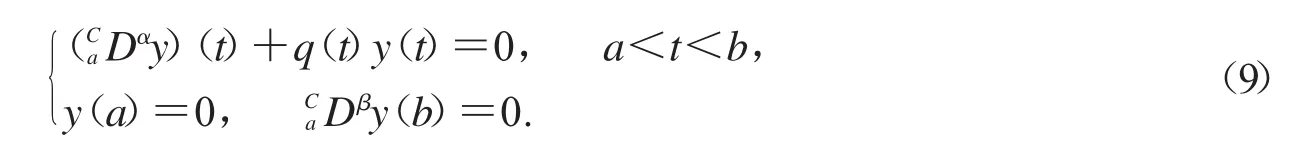
这里1<α≤2,0<β≤1,并且q:[a,b]→R是一个连续函数.若式(9)存在非奇异解,则
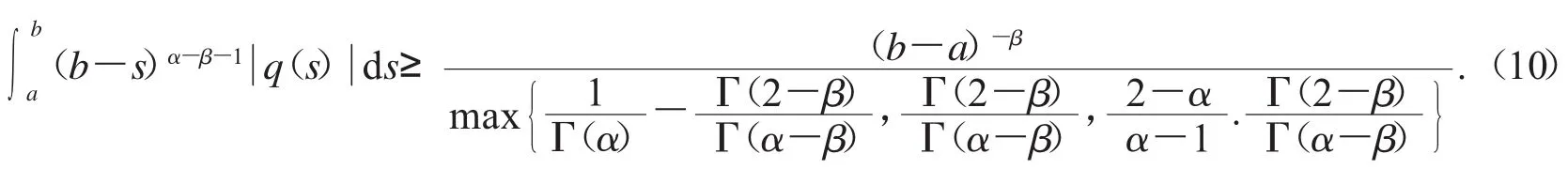
在文献[1-5]的影响下,我们将研究一类包含Caputo分数阶导数的边值条件情况下的Caputo分数阶微分方程:
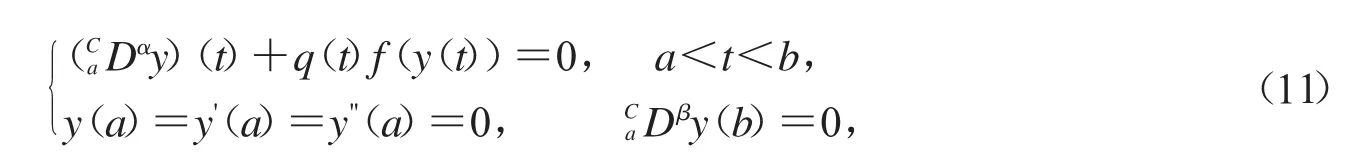
这里3<α≤4,1<β≤2,q:[a,b]→R是一个连续函数.
1 预备知识
定义1.1令α>0,Γ(α)是一个Gamma函数,定义为则函数y(t)的α阶Riemann-Liouville分数阶积分定义为
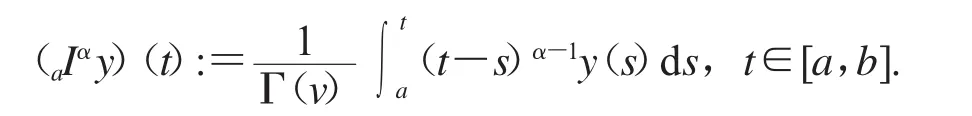
定义1.2令α>0,n=[α]+1,这里[α]是α的整数部分,则函数y(t)的α阶Caputo分数阶微分定义为
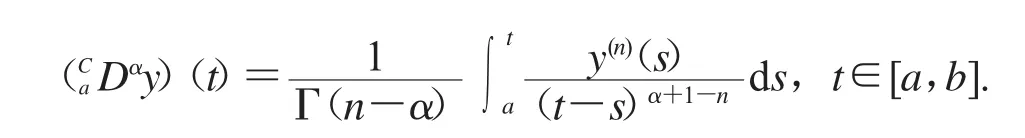
引理1.1令γ>α>0,f∈C[a,b],则
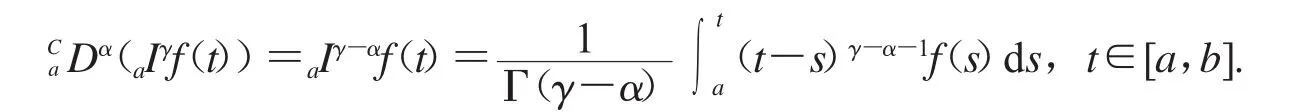
引理1.2令y∈C[a,b],且3<α≤4,则
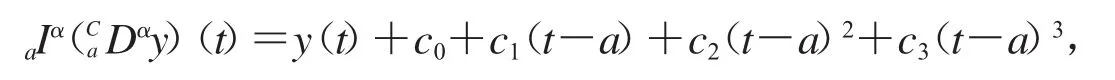
这里c0,c1,c2,c3是实常数.
引理1.3[6]假设K(x,t)在区间[a,b]×[a,b]上是连续的,且对于任意固定的t∈[a,b],K
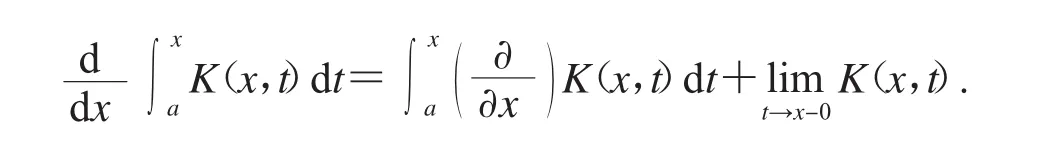
引理1.4 y∈C[a,b]是边值问题式(11)的解,当且仅当y满足下面积分不等式
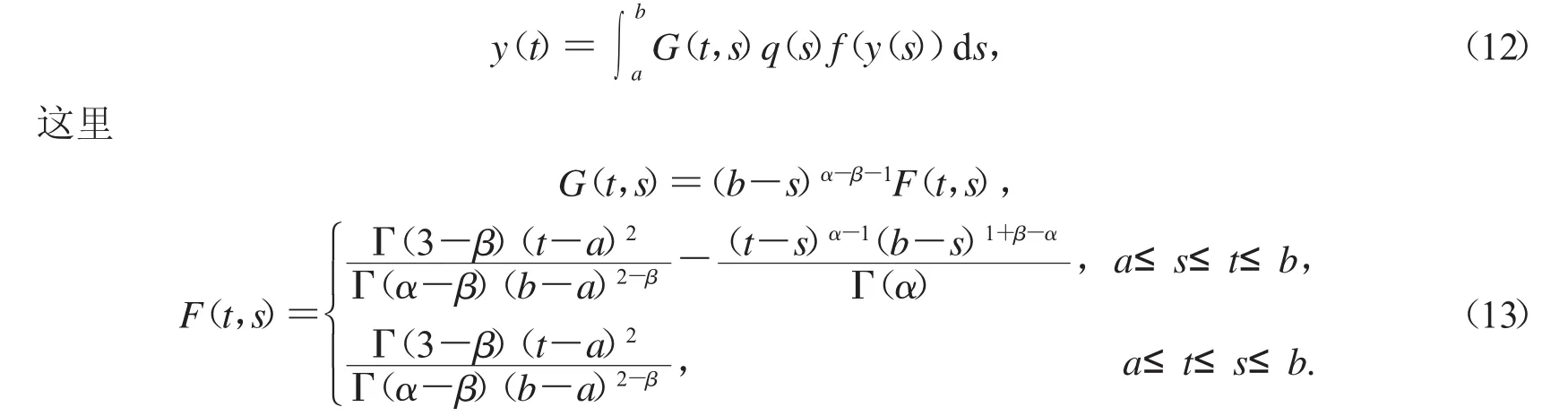
证明:对式(11)两边做积分运算,则由引理1.2,我们有
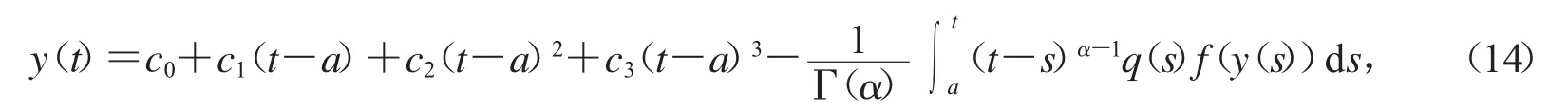
根据条件3<α≤4和y(a)=0,我们有c0=0.
因此
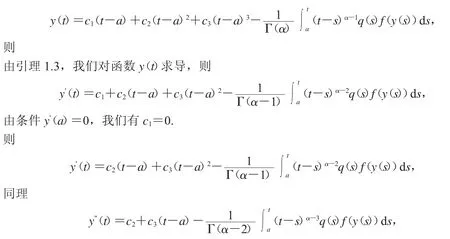
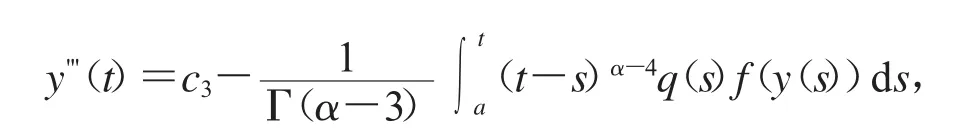
由条件yquot;(a)=0,我们有c3=0.因此,我们有
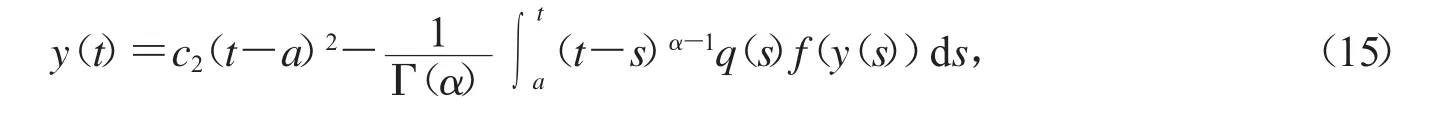
然后对式(15)两边求导,由定义1.2,我们有
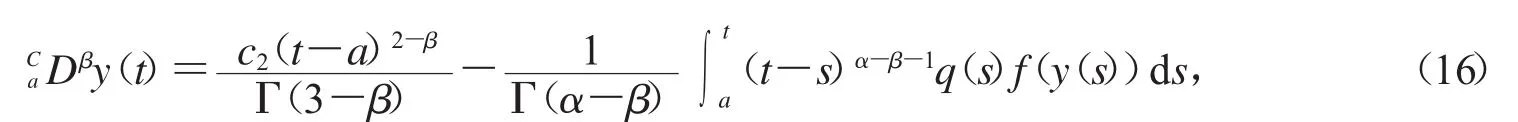
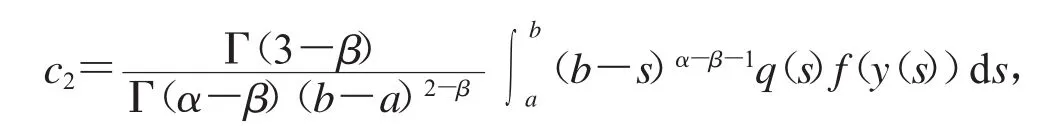
把上式代入式(14),我们有
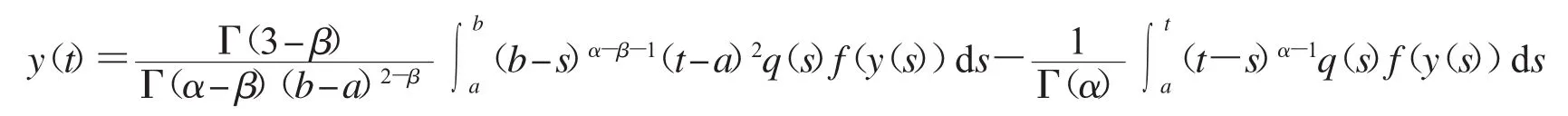
证毕.
引理1.5对∀(t,s)∈[a,b]×[a,b],我们有
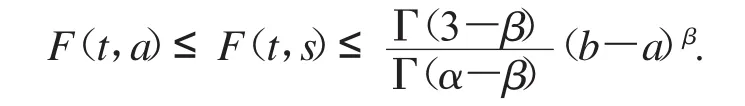
证明:当a≤s≤t≤b时,
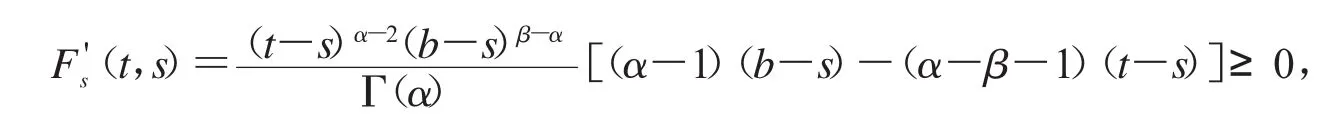
故对于s∈[a,t],我们有
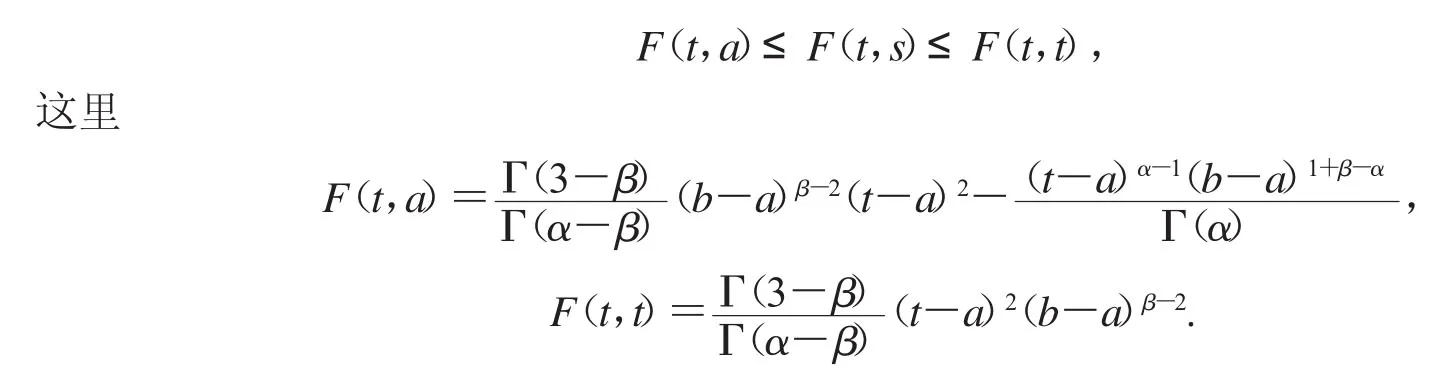
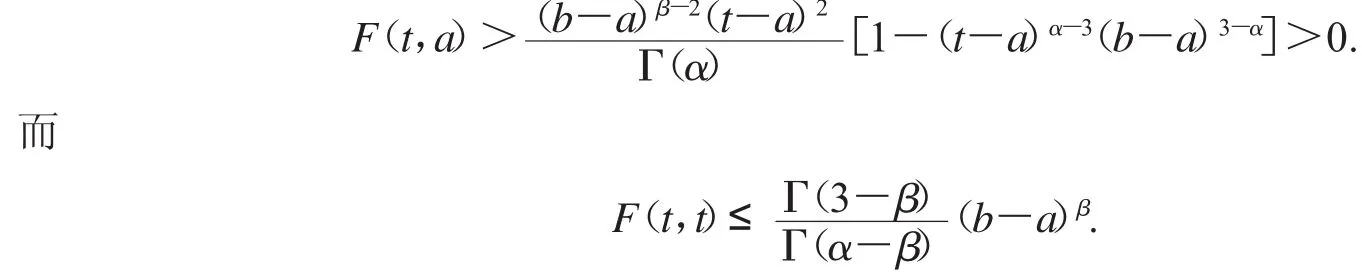
因此对于s∈[a,t],我们有
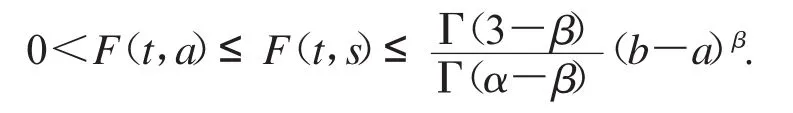
当a≤t≤s≤b时,F(t,s)≥0显然成立,且
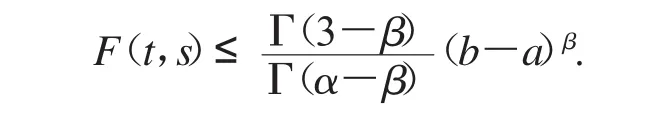
综上,对∀(t,s)∈[a,b]×[a,b],
成立,证毕.
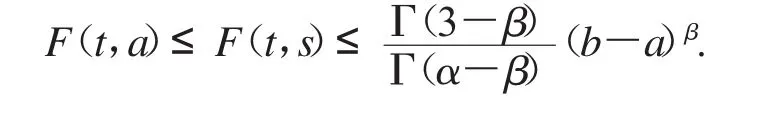
2 主要结论
这个部分将给出Lyapunov-type不等式及一些推论.
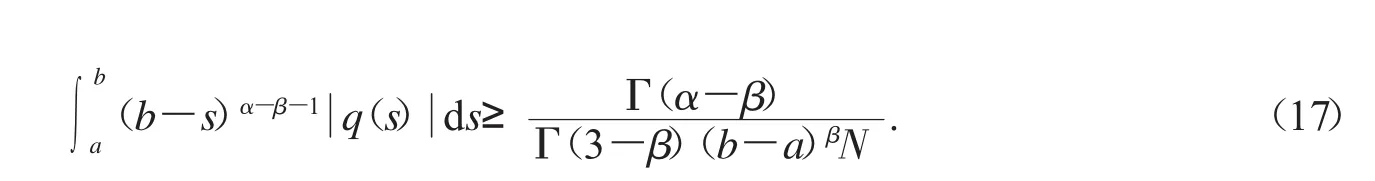
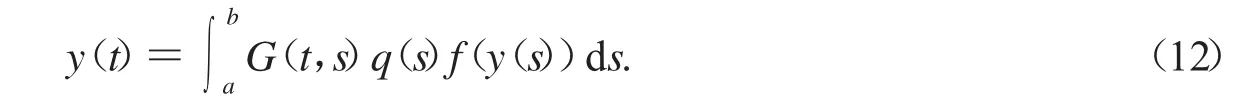
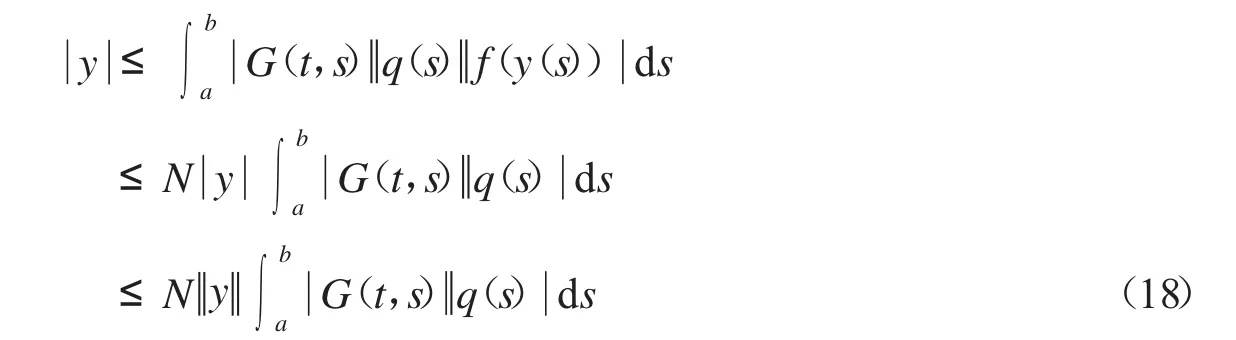
把引理1.5运用到式(18),我们有
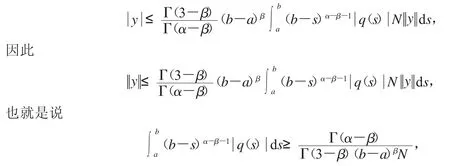
证毕.
除此之外,在式(11)中令f(y)=y,我们得到下面带线性项的分数阶边值问题.
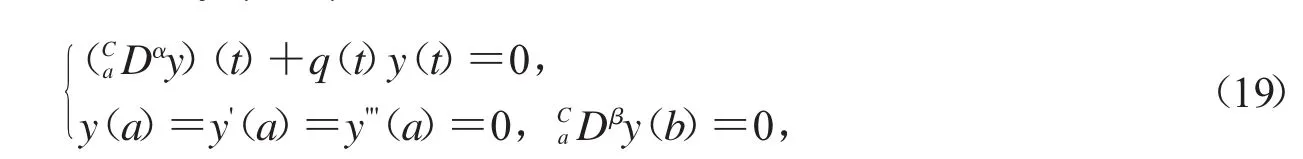
这里3<α≤4,1<β≤2,q:[a,b]→R是一个连续函数.
现在,我们令N=1,并且由定理2.1,我们得到如下推论.
推论2.1如果式(19)有一个非奇异解y∈[a,b],则
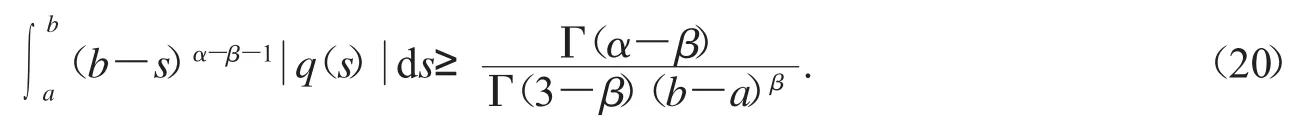
推论2.2若β=2,则由式(17)推导出下面Lyapunov-type不等式:
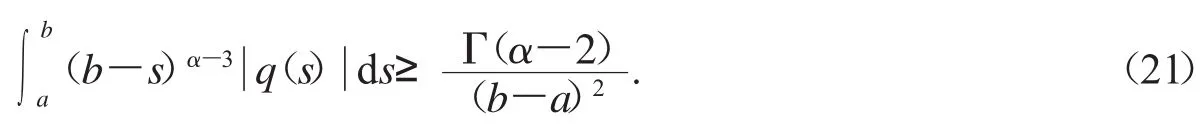
推论2.3若α=4,1<β≤2,由引理1.4,我们有
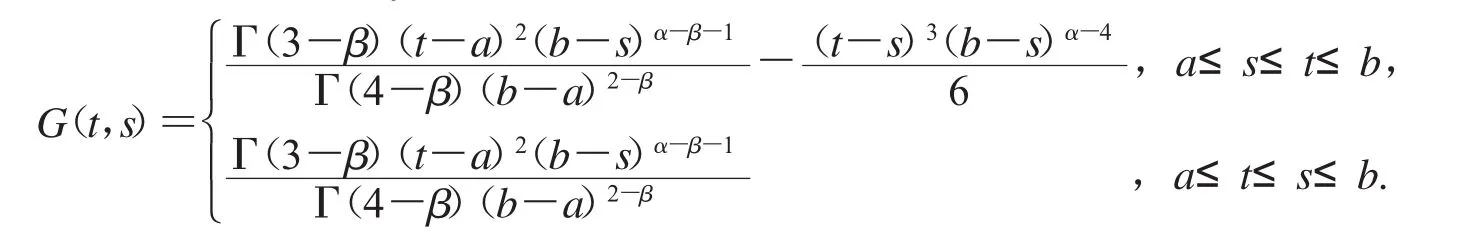
则由式(17)推导出下面Lyapunov-type不等式:
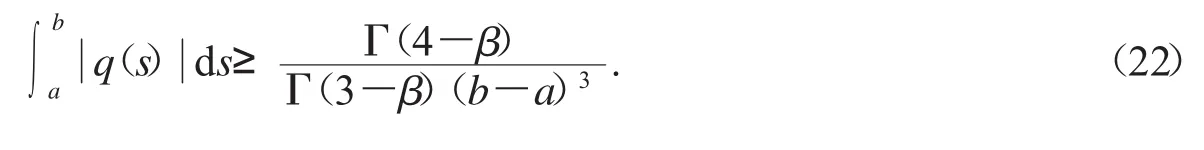
3 应用
3.1 特征值问题
在式(19)中令a=0,b=1,然后我们讨论下面特征值问题
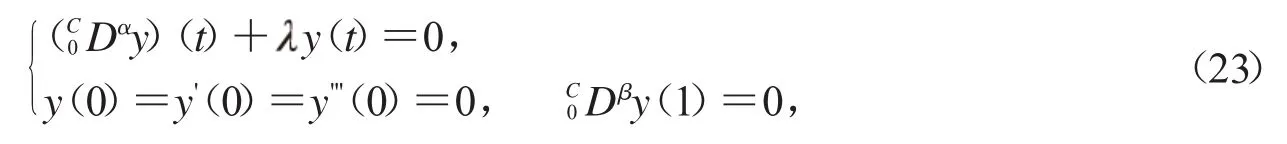
这里3<α≤4,1<β≤2.
由推论2.1,我们得到下面推论.
证明:假设y0(t)是式(23)中对应特征的一个特征函数.由推论2.1中的式(20),我们有矛盾.
3.2 对于某些Mittag-Leffler函数的实零点
现在,我们考虑下面含有两个参数的Mittag-Leffler函数
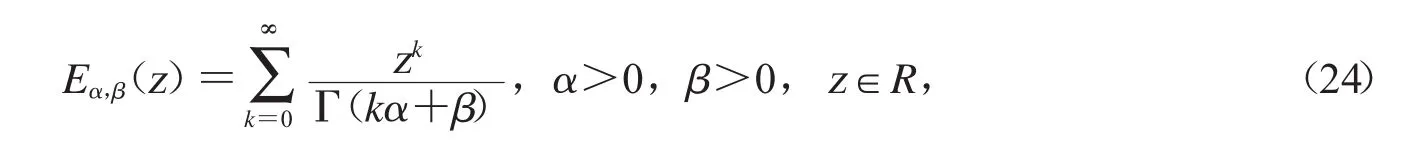
显然,对于任意的z≥0,都有Eα,β>0.因此,对于Eα,β的实零点,如果存在,一定是一个负实数.对于Mittag-Leffler函数,参数1<β≤2,3<α≤4时,我们将用推论2.1去求函数没有实零点的区间.
证明:由文献[7]中的定理1,式(23)中通解y(t)为
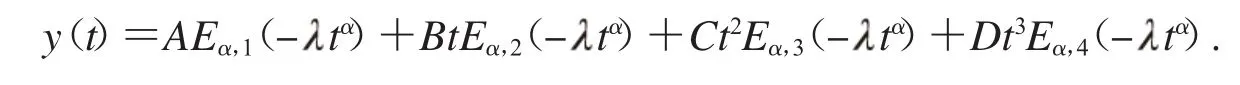
由式(23)中边值条件,我们有
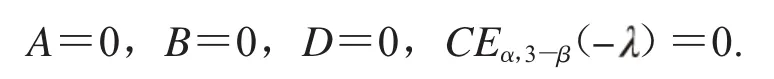
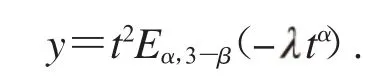
4 结论
对于下面非线性分数阶微分方程的边值问题,我们得到一个Lyapunov-type不等式
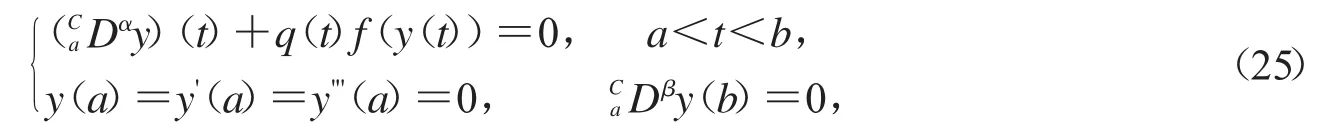
这里3<α≤4,1<β≤2,q:[a,b]→R是一个连续函数.
我们假设非线性项f是可控制的,故由上面定理,得到这些不等式.在证明这些不等式的过程中,得到格林函数的准确性质是很重要的.
下面特征值问题
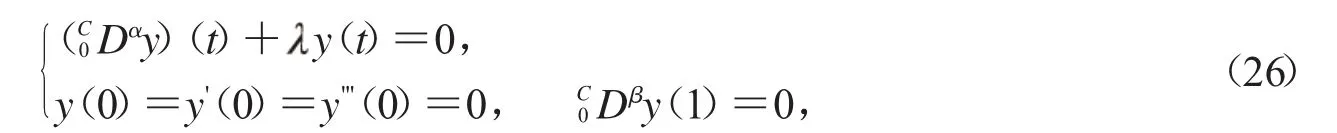
这里3<α≤4,1<β≤2.没有对应的特征函数y(t);另一方面,我们得到对于,Mittag-Leffler函数没有实零点.
[1]LYAPUNOV A M.Problème général de la stabilité du movement[J].Ann Fac Sci Univ Toulouse,1907,9:203-474.
[2]FERREIRA R A C.On a Lyapunov-type inequality and the zeros of a certain Mittag-Leffler function[J]. Journal of Mathmatics and Applications.2014,412(2):1058-1063.
[3]O’REGAN D,SAMET B.Lyapunov-type inequalities for a class of fractional differential equations[J]. Journal of Inequalities and Applications,2015,247:1-10.DOI:10.1186/s13660-015-0769-2.
[4]JLELIM,SAMETB.Lyapunov-type inequalities for a fractional differential equation with mixed boundary conditions[J].Mathematical Inequalities and Applications,2015,18(2):443-451.
[5]RONG J,BAI C.Lyapunov-type inequality for a fractional differential equation with fractional boundary conditions[J].Advances in Difference Equations,2015,2015:82.DOI:10.1186/s13662-015-0430-x [6]KILBAS A A,SRIVASTAVA M H,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterdam:Elsevier Science B V,2006:78.
[7]KILBASAA,RIVEROM,RODRIGUEZ-GERMAL,etal.Caputolinear fractional differential equation[C]// IFACProceeding,2006[2017-04-01].https://www.researchgate.net/publication/236221333.DOI:10.4203/ ccp.84.15.
[8]FERREIRA R A C.A Lyapunov-type inequality for a fractional boundary value problem[J].Fractional Calculus and Applied Analysis,2013,16(4):978-984.
[9]JLELI M,LAKHDAR R,SAMET B.A Lyapunov-type inequality for a fractional differential equation under a Robin boundary condition[J].Journal of Function Spaces,2015,2015(1):1-5.DOI:10.1155/ 2015/468536
[10]PODLUBNY I.Fractional differential equations[M].San Diego:Academic Press,1999.
[11]LIANG S,ZHANG J.Positive solutions for boundary-value problems of nonlinear fractional differential equations[J].Journal of Differential Equation,2009,71(11):5545-5550.
[12]白占兵.分数阶微分方程边值问题理论及应用[M].北京:中国科技出版社,2013.
[13]郭大钧,非线性泛函分析[M].济南:山东科技出版社,1985.
[14]MILLER K S,ROSS B.An introduction to the fractional calculus and fractional differential equations [M].New York:Wiley,1993.
[15]DUAN J S,WANG Z,LIU Y L,et al.Eigenvalue problems for fractional ordinary differential equations[J].Chaos Solitons Fractals,2013,46(1):46-53.
[16]YANG X,KIM Y,Lo K.Lyapunov-type inequality for a class of linear differential systems[J].Applied Mathmatics Computation,2012,219(4):1805-1812.
Lyapunov-Type Inequality for a Fractional Differential Equation with Boundary Value Problem
WU Zhongwen,MA Dexiang
(Department of Mathematics,North China Electric Power University,Beijing102206,China)
A Lyapunov-type inequality for a Caputo fractional differential equation under boundary condition involving the Caputo fractional derivative is established.Firstly,according to Caputo fractional derivative definitions,a fractional equation is transformed into its equivalent integral equation,according to the boundary value conditions to get the corresponding Green function.In order tofacilitate the studyofthe nature ofthe Green function,the function F(t,s)is extracted.Byusing the method ofderivative in mathematical analysis,the properties offunction F(t,s)is studied toget the upper and lower bounds ofthe function over the whole interval.Finally,as application,for a fractional differential equation eigenvalue problem,a bound of the eigenvalue is obtained.Then,for certain Mittag-Leffler function,an interval where has noreal zeros is gotten.
fractional differential equation;Lyapunov-type inequality;Green function;Mittag-Leffler function
1001-4217(2017)04-0048-08
O 175.1
A
2017-04-03
武忠文(1992—),女(汉族),安徽淮南人,硕士,研究方向:分数阶微分方程.E-mail:2672105752@qq.com
