聚焦集合知识中的易错点
2017-11-27江苏省南京市溧水区第二高级中学金志胜
■江苏省南京市溧水区第二高级中学 金志胜
聚焦集合知识中的易错点
■江苏省南京市溧水区第二高级中学 金志胜
编者的话:同学们在学习的过程中,难免会出现错解的现象。本期“易错题归类剖析”栏目推出的文章,注重剖析错解原因,注重补充知识缺陷,注重题目引申变换,希望同学们认真领会,学以致用,不再发生类似的错解。
集合作为一种数学语言和工具在数学问题中被广泛地应用。在实施集合语言等价转换过程中,有些同学由于不能深刻理解集合的意义、性质、表示法或考虑问题不全,而常造成错解。下面就常见的易错点进行归纳剖析,并给出提醒,希望对同学们的学习能有所帮助。
聚焦1——忽视集合中的代表元素的特征
例1 已知A={y|y=2x+1,x∈R},B={(x,y)|y=x2+1,x∈R},则有( )。
A.A∩B={(0,1),(2,5)}
B.A⊆B
C.B⊆A
D.A∩B=∅
错解:选A或C。
剖析:没有注意到集合中代表元素的特征,将数集与点集混淆,应把握集合的代表元素。集合A是数集,集合B是点集,根本没有相同的元素,因此,A∩B=∅,选D。
提醒:集合是由元素构成的,认识集合要从认识元素开始,集合里的元素可以是数、物、有序实数对、几何图形等;关键要弄清集合的代表元素和代表元素的属性。
跟踪练习1 已知函数y=f(x),x∈[a,b],那么集合{(x,y)|y=f(x),x∈[a,b]}∩{(x,y)|x=2}中元素的个数为( )。
A.1 B.0 C.0或1 D.1或2
易错点:没有弄清两个集合的代表元素,蒙出答案D。
正解:{x|y=f(x)}、{y|y=f(x)}、{(x,y)|y=f(x)}分别表示函数y=f(x)的定义域、值域、函数图像上的点的坐标组成的集合。本题中集合的含义是两个图像交点的个数,从函数值的唯一性可知,两个集合的交集中至多有一个交点,故选C。
聚焦2——忽视空集∅的存在性
例2 已知集合A={x|x2-5x+4≤0},B={x|x2-2a x+a+2≤0},并且B⊆A,求实数a的取值范围。
错解:由条件x2-5x+4≤0,可得A={x|1≤x≤4}。
设f(x)=x2-2a x+a+2≤0,则f(x)=0的两根在区间[1,4]内。由B⊆A得方

剖析:上述解法只注意到了B为非空集合,忽视了B=∅的情况。当B=∅时,仍满足B⊆A。①当B≠∅时,由错解可得2≤a≤。
②当B=∅时,可得一元二次方程x2-2a x+a+2=0的Δ=4a2-4(a+2)2<0,由此解得-1<a<2。
提醒:对于空集∅,在解题时必须注意它的三个特性:①对任意集合A,皆有A∩∅=∅;② 对任意集合A,皆有A∪∅=A;③ 空集是任何集合的子集,即∅⊆A,空集是任何非空集合的真子集 ,即∅A。解题时,若忽视空集∅的存在性,就会造成解题结果的残缺不全。
易错点:A∩B=A或A∪B=A中,易忽略A=∅的情形或集合的隐含条件,从而导致漏解。
正解:由A∩B=A,当A≠∅时,有A⊆

当A=∅时,有m+1≥2m-1,解得m≤2。
综上,有m≤3。
聚焦3——忽视集合转化的等价性
例3 已知集合A={x|a x2+2x+1=0}为一元集,求a的值。
错解:集合A为一元集,即方程a x2+2x+1=0有两等根,由Δ=4-4a=0,得a=1。
剖析:上述解法误认为所给方程为一元二次方程,忽视了对二次项系数的讨论。
当a≠0时,由Δ=4-4a=0,得a=1;当a=0时,可得也符合题意。所以a=1或a=0。
提醒:在进行集合转化时,要注意转化的等价性,否则就会产生增解或漏解。
跟踪练习3 (2 0 1 7年浙江温州高三模拟)已知集合M={(x,y)|x2+y2≤1},若实数λ,μ满足:对任意的(x,y)∈M,都有(λ x,μ y)∈M,则称(λ,μ)是集合M 的“和谐实数对”,则以下集合中,存在“和谐实数对”的是( )。
A.{(λ,μ)|λ+μ=4}
B.{(λ,μ)|λ2+μ2=4}
C.{(λ,μ)|λ2-4μ=4}
D.{(λ,μ)|λ2-μ2=4}
易错点:缺少“和谐实数对”的等价转化,实际上它可以转化为平面区域与直线、圆和双曲线的交点。
正解:分析题意可知,所有满足题意的有序实数对(λ,μ)所构成的集合为{(λ,μ)|-1≤λ≤1,-1≤μ≤1},将其看作点的集合,为中心在原点,(-1,1),(-1,-1),(1,-1),(1,1)为顶点的正方形及其内部,A、B、D选项分别表示直线、圆、双曲线与该正方形及其内部无公共点,选项C为抛物线,有公共点(0,-1),故选C。
聚焦4——求解否定型或正面较复杂的集合问题缺少“补集”思想的应用
错解:有些同学遇到本题往往不知所措,不知道从其反面逆向思维,导致无法解决。
剖析:从反面入手,利用元素和集合之间的关系进行切入,3∉P,则3∈∁RP,∁RP=3a+2≤a,所以a≤-1,即a的取值范围是(-∞,-1]。
提醒:已知全集U,若直接求其子集A有困难,则可先考虑其补集∁UA,再利用∁U(∁UA)=A而间接求出A。这种在正向思维受阻后改用逆向思维的思想,就是数学上的补集思想方法。从哲学意义上讲,它是通过两次否定实现一次肯定,体现了否定之否定规律。
跟踪练习4 已知集合P={x|4≤x<5,x∈R},Q={x|k+1≤x<2k-1,x∈R},当P∩Q≠Q时,求实数k的取值范围。
易错点:缺少“补集”思想的应用,直接求解无从下手。
正解:从反面入手,当P∩Q=Q,则Q⊆P。
当Q=∅时,满足Q⊆P,此时k+1≥2k-1,解得k≤2;
由上可知,当P∩Q=Q时,k≤2。
由补集思想可知,当P∩Q≠Q时,k>2,即所求实数k的取值范围是(2,+∞)。
聚焦5——忽视数轴和韦恩图可以形象地求解集合问题
例5 对某村家庭拥有洗衣机、电冰箱、电视机的情况进行调查统计,统计表如表1,那么该村中,拥有三种电器的家庭与全村家庭总数的比例应为多少?

表1
错解:本题所给的为三个集合之间的关系,比较错综复杂,难以下手。
剖析:利用韦恩图(图1)形象地表示出各数量间的关系,将文字语言翻译成集合语言,用“容斥原理”求解。设全村家庭总数为1 0 0,A={洗衣机}=7 2,B={电冰箱}=6 4,C={电视机}=8 0,A∩B={洗衣机和电冰箱}=5 2,A∩C={洗衣机和电视机}=5 6,B∩C={电冰箱和电视机}=5 2______。
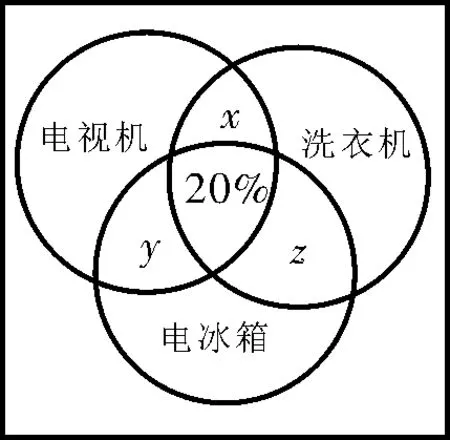
图1
由表1可知,n(A∪B∪C)=2,由“容斥原理”和表1,有n(A∪B∪C)=9 8,且9 8=7 2+6 4+8 0-5 2-5 6—5 2+n(A∩B∩C),解得n(A∩B∩C)=4 2,故拥有三种电器的家庭与全村家庭总数的比例应为4 2%。
提醒:韦恩图可以形象地反映三个集合之间的关系,即 “容斥原理”,三个集合并集个数n(A∪B∪C)=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)+n(A∩B∩C)。用此结论计数可避免重复和遗漏。数轴和韦恩图可以形象地反映变量范围和变量之间的关系,为数形结合法研究集合问题提供了方法和依据,同学们要自觉养成这种习惯。
跟踪练习5 某高级中学高三特长班有1 0 0名学生,其中学绘画的学生6 7人,学音乐的学生4 5人,而学体育的学生既不能学绘画,又不能学音乐,人数是2 1人,那么同时学绘画和音乐的学生有多少人?
易错点:所给的数量关系比较错综复杂,一时理不清头绪,不好找线索。
正解:利用韦恩图(图2)形象地表示出各数量间的关系,设学绘画的学生有x人,学音乐的人有y人,既学绘画又学音乐的人有



图2
所以,同时学绘画和音乐的有3 3人。
聚焦6——新定义集合计数中混淆分类和分步
A.4 B.8 C.9 D.1 6
错解:由A∩B=1,3{},从元素2,4中不取,取1个,取2个,则共有1+2+1=4(个),选A。
剖析:错解按求子集个数分类完成致错,由理解“理想配集”的意义,应从元素2和4所在集合的情形连续分步完成,元素1,3既属于A,又属于B,考虑元素2,有3种可能:(1)2∈A,2∉B;(2)2∉A,2∈B;(3)2∉A,2∉B。再考虑元素4,同样有3种可能,2和4需连续完成才能构成“理想配集”,所以符合条件的“理想配集”的个数为3×3=9,故选C。
提醒:求解集合元素个数题的关键是过好双关:第一关,分类讨论关,即对集合中的元素所具有的特点,分类进行讨论;第二关,统计关,即利用排列组合的公式,计算此集合中的元素的总的个数。在新定义的集合组成中要注意分类和分步的区别,一种方法能完成这件事用分类计数,一种方法能完成这件事的某一步用分步计数,分类时应把握分类的标准,分步时应清楚分步过程,本题还可对元素逐一列举完成求解,同学们不妨一试。
跟踪练习6 (2 0 1 7年福建泉州段考)若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)是集合A的同一种分拆。若集合A有三个元素,则集合A的不同分拆种数是____。
易错点:对新定义集合计数缺少特殊化和列举法尝试的意识。
正解:设A=1,2,3{ }。
①若A1=∅时,此时只有1种分拆。
②若A1是单元素集时,A共有6种分拆:{1}与{2,3},{1}与{1,2,3},{2}与{1,3},{2}与{1,2,3},{3}与{1,2},{3}与{1,2,3}。
③若A1是双元素集时,A共有1 2种分拆:{1,2}与{3},{1,3},{2,3},{1,2,3};{1,3}与{2},{1,2},{2,3},{1,2,3};{2,3}与{1},{1,2},{1,3},{1,2,3}。
④若A1=A={1,2,3}时,A共有8种分拆:{1,2,3}与∅,{1},{2},{3},{1,2}{1,3},{2,3},{1,2,3}。
综上,共有1+6+1 2+8=2 7(种)。
聚焦7——对新定义集合的属性探究不彻底
例7 设S为满足下列条件的实数构成的非空集合:①1∉S;②若a∈S,则问:集合S中至少有多少个元素?试证明你的结论。
错解:假设0为集合S中的元素,并把它当作条件做进一步分析。若0∈S,则1∈S,从而可得这是不可能的,所以集合S中至少有一个元素0。

提醒:本题是结论开放性问题,题目的特点是结论不确定,集合A的特点是它的元素随着实数a(a≠0,a≠1)的变化而变化。解题时,要注意在假设存在的条件下进行推理,若由此导出矛盾,则否定假设,否则,给出肯定的结论。同时,要对集合A中的元素的确定性和互异性加以归纳证明。
跟踪练习7 (2 0 1 7年广东揭阳模拟)非空数集A如果满足:①0∉A;② 若∀x∈A,有
∈A,则称A是“互倒集”。给出以下数集:
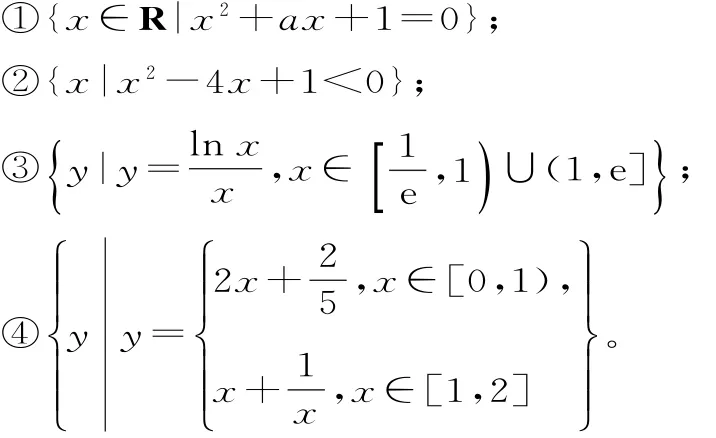
其中“互倒集”的个数是( )。
A.4 B.3 C.2 D.1
易错点:对新定义集合的属性应用不彻底。
正解:对集合①,当-2<a<2时为空集,所以集合①不是“互倒集”;

(责任编辑 王福华)
