数列常见思维误区辨析

■河南省商丘市第三高级中学 孟庆芬

数列常见思维误区辨析

■河南省商丘市第三高级中学 孟庆芬

数列是历年高考的重点内容,作为一种特殊的函数,这部分内容的易错点多,同学们容易陷入思维的误区,且不易察觉。下面对常见的易错题型进行剖析、找出错因,希望对同学们的学习有所帮助。

一、忽略数列的定义域为N*而致错

错因分析:上述解法仅考虑了函数y=f(x)在[1,+∞)是单调递增的情形,忽略了数列作为函数的一种,其定义域为N*的特殊性。其实,考虑数列的n∈N*,n的取值是离散的,只需要满足an=f(n)(n∈N*)在[1,7],[8,+∞)上分别递增,且a7＜a8即可。

总结:从函数观点看,数列是定义在正整数集N*或其子集上的函数,其图像是一列离散的点,数列的单调性可以借助函数的单调性进行考虑,但是要注意其特殊性,借助图像,避免出错。

二、忽略等比数列的隐含条件而致错

等比数列{an}中,S2=7,S6=91,求S4的值。

错解:因为{an}为等比数列,S2=7,S6=91,从而q≠-1,S2,S4-S2,S6-S4成等比数列,于是有(S4-S2)2=S2·(S6-S4),解得S4=28或S4=-21。

错因分析:错解忽略了数列S2,S4-S2,S6-S4的公比为原数列{an}的公比q的平方,所以S2,S4-S2,S6-S4这三项是同号的。

正解:因为{an}为等比数列,S2=7,S6=91,从而q≠-1,S2,S4-S2,S6-S4成等比数列,于是有(S4-S2)2=S2·(S6-S4),解得S4=28或S4=-21,又S4-S2=q2S2,故S4=28。

总结:等比数列有很多特殊性。(1)在定义中可以得出:0不会出现在等比数列中,公比q≠0。(2)等比数列的所有奇数项都同号,所有的偶数项都同号。做题时要充分考虑这些特性,以避免出错。

三、对前n项和的理解错误而致错

则a11=S11-S10=(7×11+1)k-(7×10+1)k=7k。

b11=T11-T10=(4×11+27)k-(4×10+27)k=4k。

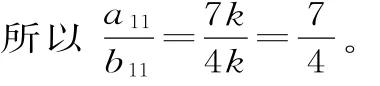
错因分析:“设Sn=(7n+1)k,Tn=(4n+27)k,k≠0”这种设法虽然可以成立,但是错在认为k是与n无关的常数。其实由等差数列的前n项和公式Sn=d≠0时,Sn是关于n的一元二次函数,且常数项为0。故应设Sn=(7n+1)kn,Tn=(4n+27)kn才与等差数列的前n项和的特点相符合。

正解:设Sn=(7n+1)kn,Tn=(4n+27)kn,k≠0。

a11=S11-S10=(7×11+1)k×11-(7×10+1)k×10=148k。

b11=T11-T10=(4×11+27)k×11-(4×10+27)k×10=111k。

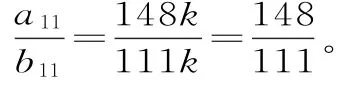
总结:正确把握等差数列前n项和的特点,从求和公式出发求解,才能正确解决这类问题。

四、利用an=Sn－Sn－1求数列的通项公式时忽视条件n≥2而致错

已知数列{an}的前n项和为Sn,且Sn=n2+4n+3,试判断数列{an}是否为递增数列,并说明理由。

错解:数列{an}是递增数列,理由如下:

因为an=Sn-Sn-1=2n+3,所以an+1-an=2(n+1)+3-(2n+3)=2＞0。故数列{an}是递增数列。

错因分析:求解本题时,应明确an=Sn-Sn-1成立的条件是n≥2,数列an{}的通项公式中的an应包含第一项a1,所以an+1-an＞0(n≥2)只能说明数列{an}是从第2项开始的递增数列,所以对于n=1时是否满足要求应该进行验证。

正解:数列an{}不是递增数列,理由如下:

因为a1=S1=8,an=Sn-Sn-1=2n+3(n≥2),当n=1时,2n+3=5≠8,所以an=当n=2时,a2=2×2+3=7＜a1,故数列{an}不是递增数列。

总结:数列的通项公式an与前n项和公式Sn的关系是Sn-Sn-1求an时,成立的条件是n≥2,应先求出通项公式,决定通项公式是否为分段形式,再判断函数的单调性。

五、对求和公式的适用条件把握不准致错

求和a-1( )+a2-2( )+a3-3( )+…+an-n( )。

错解:令 Sn=a-1( )+a2-2( )+a3-3( )+…+an-n( )。

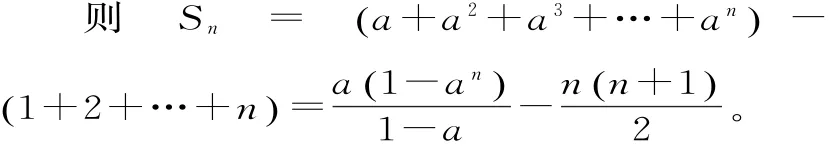
错因分析:错解中,计算a+a2+a3+…+an的和时,由于对数列a,a2,a3,…,an的性质不清楚,忽略了对a的分类讨论而导致出错。

正解:令Sn=a-1( )+a2-2( )+a3-3( )+…+an-n( )。

则 Sn=a+a2+a3+…+an(

)-1+2+…+n()。

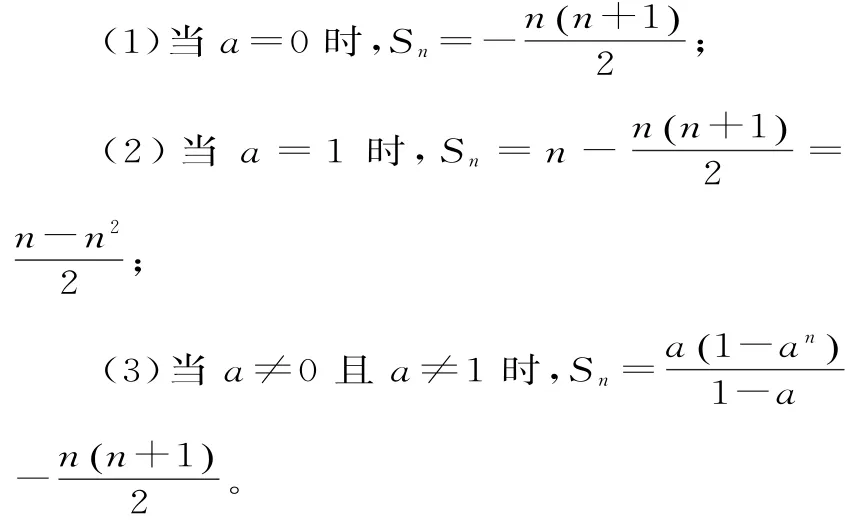
综上所述,得:

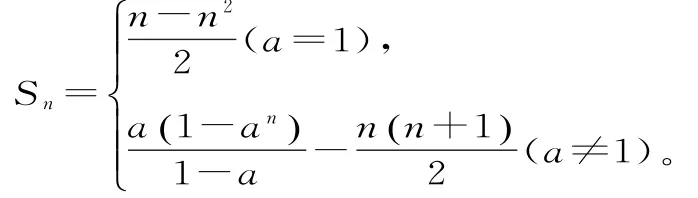
总结:利用等比数列的求和公式Sn=求数列的前n项和时,首先要确定数列是否为等比数列,若是等比数列,应对公比q进行分类讨论,最后结果化为最简形式。

(责任编辑 赵 平)