小议创新题的“三新”

■湖北省巴东县第三高级中学 廖庆伟

小议创新题的“三新”

■湖北省巴东县第三高级中学 廖庆伟

编者的话:“创新题追根溯源”栏目里的例、习题都非常新颖,有的是原创题,有的是改编题,每一道题都非常注重多解多变。当然,在注重数学阅读的高考大背景下,同学们还要把握核心考点,扩大知识视野,用扎实的基本功应对数学试题的万千变化。

数学中的创新题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的。

一、新定义

首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是破解新定义型集合问题的关键所在。

例1 设S,T是R的两个非空子集,如果存在一个从S到T的函数y=f(x)满足:①T={f(x)|x∈S};②对任意x1,x2∈S,当x1＜x2时,恒有f(x1)＜f(x2),那么称这两个集合“保序同构”。以下集合对不是“保序同构”的是( )。

A.A=N*,B=N

B.A={x|-1≤x≤3},B={x|x=-8或0＜x≤1 0}

C.A={x|0＜x＜1},B=R

D.A=Z,B=Q

解析:对于选项A,可构造函数f(x)=x-1,x∈N*,验证成立;对于选项B,可构造函数验证成立;对于选项C,可构造函数f(x)=,验证成立;选项D是错误的。

点评:本题以集合为媒介,通过新定义考查集合间的关系,考查同学们的理解能力,学习新知识、运用新知识的能力。

例2 设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”。若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为____。

解析:由题意知,y=f(x)-g(x)=x2-5x+4-m在[0,3]上有两个不同的零点。在同一直角坐标系下作出函数y=m与y=x2-5x+4(x∈[0,3])的图像,如图1所示,结合图像可知,当x∈[2,3]时,y=x2-5x+数y=m与y=x2-5x+4(x∈[0,3])的图像有两个交点。

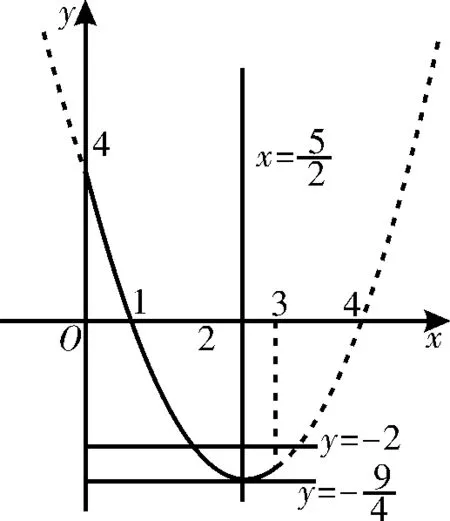
图1

点评:本题通过新定义的关联函数,考查二次函数的图像性质、函数的零点。考查学习新知识、运用新知识求解问题的能力。

例3 给出定义:若函数f(x)在D上可导,即f'(x)存在,且导函数f'(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f'(x))'。若f″(x)＜0在D上恒成立,则称f(x)在D上为凸函数。以下四个函数在上为凸函数的是____(把你认为正确的序号都填上)。

①f(x)=s i nx+c o sx;

②f(x)=l nx-2x;

③f(x)=-x3+2x-1;

④f(x)=xex。

解析:①中,f'(x)=c o sx-s i nx,f″(x)=-s i nx-c o sx=-2 ·上恒成立;②中,在区间上恒成立;③中,f'(x)=-3x2+2,f″(x)=-6x＜0在区间上恒成立。故①②③为凸函数。④中,f'(x)=ex+xex,f″(x)=2 ex+xex=ex(x+2)＞0在区间上恒成立,故④不是凸函数。故四个函数在上为凸函数的是①②③。

点评:本题通过新定义的凸函数,考查阅读理解能力以及用导数知识求解问题的能力。

二、新运算

通过题目引入的新符号,定义运算法则,把问题转化为已经学过的知识,再求解,这个新的运算法则不能用于其他问题的求解。

例4 对于任意两个正整数m,n,定义运算(用⊕表示运算符号):当m,n都是正偶数或都是正奇数时,m⊕n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m⊕n=m×n。例如4⊕6=4+6=1 0,3⊕7=3+7=1 0,3⊕4=3×4=1 2。在上述定义中,集合M={(a,b)|a⊕b=1 2,a,b∈N*}的元素有______个。

解析:m,n同奇同偶时有1 1组:(1,1 1),(2,1 0),…,(1 1,1);m,n一奇一偶时有4组:(1,1 2),(1 2,1),(3,4),(4,3),所以集合M的元素共有1 5个。

点评:集合M的元素个数要根据定义的运算法则,分别求m,n同奇同偶或一奇一偶时的元素个数,考查分类讨论思想。

例5 定义新运算⊕:当a≥b时,a⊕b=a;当a＜b时,a⊕b=b2,则函数f(x)=(1⊕x)x-(2⊕x),x∈[-2,2]的最大值等于( )。

A.-1 B.1 C.6 D.1 2

点评:本题通过定义新运算⊕:当a≥b时,a⊕b=a;当a＜b时,a⊕b=b2,求函数f(x)=(1⊕x)x-(2⊕x)的最大值,考查分段函数及函数的单调性。

三、新背景

通过一个新的背景建立恰当的数学模型,提炼数学规律。

例6 如图2所示的V e n n图中,A,B是非空集合,定义集合A#B为阴影部分表示的集合。若=3x,x＞0},则A#B为( )。

图2

A.{x|0＜x＜2}

B.{x|1＜x≤2}

C.{x|0≤x≤1或x≥2}

D.{x|0≤x≤1或x＞2}

解析:因为A={x|0≤x≤2},B={y|y＞1},A∪B={x|x≥0},A∩B={x|1＜x≤2},所以A#B=∁A∪B(A∩B)={x|0≤x≤1或x＞2},故选D。

点评:集合的交集、并集、补集运算可以借助韦恩图来表示运算对象与运算结果,这种表示方法称为集合基本运算的V e n n图法。

例7 四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图3所示。盛满酒后他们约定:先各自饮杯中酒的一半。设剩余酒的高度从左到右依次为h1,h2,h3,h4,则它们的大小关系正确的是( )。

A.h2＞h1＞h3＞h4B.h1＞h2＞h3＞h4

C.h3＞h2＞h4＞h1D.h2＞h4＞h1＞h3解析:观察图形可知,体积减少一半后,下部越细剩余酒的高度越高,最高为h2,最低为h4,应有h2＞h1＞h3＞h4。故选A。

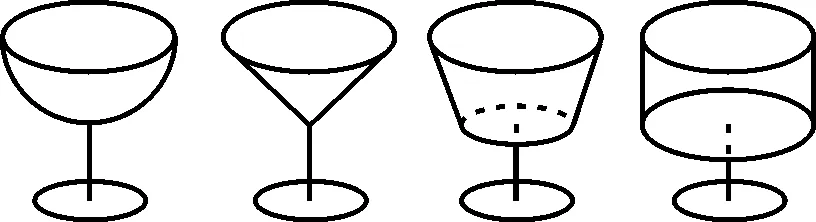
图3

点评:酒杯在我们日常生活中随处可见,2 0 0 7年江西高考题就以酒杯为背景考查分析探究能力。

(责任编辑 王福华)