基于Singer模型的高超声速飞行器轨迹跟踪与预测

魏喜庆 顾龙飞 李瑞康 王社阳

上海机电工程研究所，上海 201109

基于Singer模型的高超声速飞行器轨迹跟踪与预测

魏喜庆 顾龙飞 李瑞康 王社阳

上海机电工程研究所，上海 201109

目标运动轨迹预测有助于拦截弹在中制导准确飞往预测命中点，降低中制导修正偏差消耗的能量，对于高速高机动类目标的拦截至关重要。针对非弹道式高超声速飞行器的周期跳跃运动特点，提出了结合Singer模型的扩展卡尔曼滤波方法对目标运动状态进行估计。利用滤波估计值及双正弦和函数拟合加速度曲线，进一步递推目标运动轨迹。仿真结果表明，提出的方法对高超声速目标具有较好的弹道跟踪和预测精度。

高超声速飞行器；自适应；跟踪；轨迹预测

1 问题描述

对于高速大机动目标的拦截通常采用迎头拦截策略，其基本原理是拦截器接近目标时以反目标速度矢量的方向正面迎击目标，便于导引头截获和稳定跟踪目标，使拦截器能以较低的速度拦截高速目标；较小交会角能有效降低末制导对拦截器的过载需求。迎头拦截需要精确的预测目标轨迹，对于高速高机动类目标的拦截至关重要[1]。

由于高超声速飞行器具有较强的机动能力，因此对弹道跟踪和预报技术提出了挑战。目前，对目标轨迹预测有2种思路：采用动力学模型和采用运动学模型的轨迹预测方法。采用动力学模型的轨迹预测方法需要对目标进行动力学建模或进行特征参数拟合，并利用飞行约束条件进行弹道反设计，该方法在没有目标先验知识的条件下实现难度较大；而采用运动学模型的轨迹预测方法，对目标先验知识需求较小，但需要利用目标的持续跟踪信息[2-5]。

由于目标运动特征复杂，很难利用单一运动学模型准确描述目标的运动模型。为了预测目标轨迹，本文拟采用如下3个步骤：

1)将当前时刻的雷达观测值作为输入，利用自适应交互多模型算法对系统的状态量进行实时估计，从而获得当前时刻的状态估计；

2)利用函数逼近的方法对目标航迹进行拟合，得到目标模型；

3)利用估计的状态值作为初值外推预测目标航迹。

2 目标运动学建模

目标运动轨迹如图1所示，雷达在坐标原点实时测量目标的位置和角度信息。

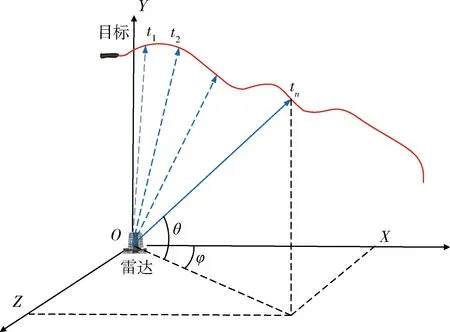
图1 目标运动示意图

目标运动学方程为：

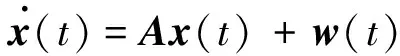
(1)

式中，x(t)=[rx(t)ry(t)rz(t)vx(t)vy(t)

vz(t)ax(t)ay(t)az(t)]T代表目标在惯性系下沿X，Y和Z轴的位置、速度和加速度，A为模型描述矩阵，w(t)为过程噪声。

量测方程为：

zk=h(xk)+vk

(2)

式中，h(xk)为地面雷达能测量到目标的位置、俯仰角和方位角，vk为量测噪声。

2.1 Singer模型

假定机动加速度a(t)为一阶时间相关过程，其时间相关函数为指数形式[6-8]：

(3)

对时间相关函数Ra(t)应用Wiener-Kolmogorov白化程序后，即动加速度a(t)可用输入为白噪声的一阶时间相关模型来表示[9-11]，即

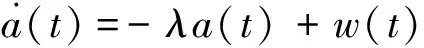
(4)

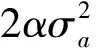
将Singer运动学模型在雷达测量坐标系下表示为：

(5)

2.2 量测模型线性化

地面雷达能测量到目标的位置、俯仰角和方位角，量测方程为

Ro=R+wR
θo=θ+wθ
φo=φ+wφ

(6)

其中，wR，wθ和wφ分别为量测噪声。雷达信息分解为雷达三轴测量方程为：

xo=Rocosθocosφo
yo=Rosinθo
zo=Rocosθosinφo

(7)

其中，xo，yo和zo均为虚拟测量值。以yo为例：

yo=Rosinθo=(R+wR)sin(θ+wθ)=
Rsinθ+Rcosθwθ+sinθwR+cosθwRwθ

(8)

其期望值和方差分别为：

E(yo)=Rsinθ

(9)

D(yo)=(Rcosθ)2D(wθ)+sin2θD(wR)+
cos2θD(wR)D(wθ)

(10)

xo，zo的概率特征求取方式相似，此处不做重复。

3 扩展卡尔曼滤波算法流程

目标运动学方程是连续系统，而量测是离散的，传感器每隔Ts时间接收到测量信息，因此实际系统采用离散卡尔曼滤波算法[12-13]。

初始化

(11)

P0=E[(x-x0)(x-x0)T]

(12)

1)时间预测

(13)

(14)

2)量测更新

(15)

(16)

(17)

假设雷达的采样周期为Ts，则

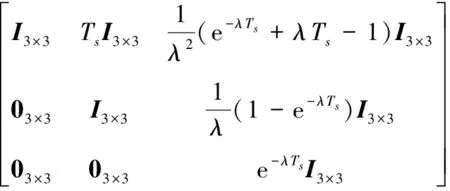
(18)

(19)

矩阵9个元素分别为：

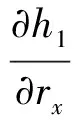
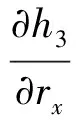
由于在扩展卡尔曼滤波算法中采用了Singer模型，因此能较好适用于带有幅值变化和频率衰减的模型状态估计。

4 仿真结果

假设雷达参数性能参数如表 1。

表1 雷达技术指标

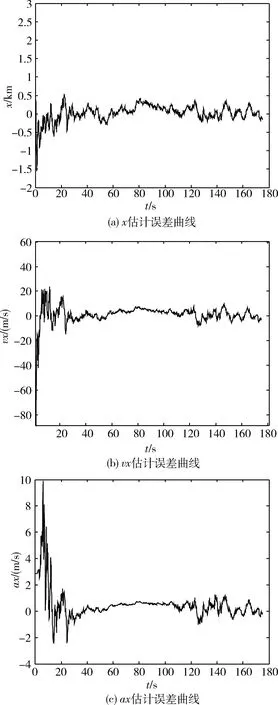
图2 X方向仿真曲线

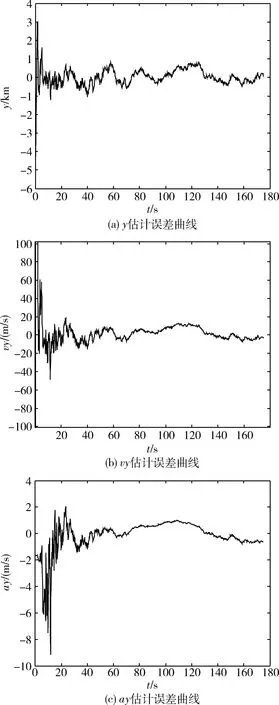
图3 Y方向仿真曲线

雷达采样频率在目标飞行的第1700s开始探测到目标，对目标持续跟踪200s后，开始预测目标轨迹。对目标X，Y或Z方向的跟踪滤波曲线分别如图2～4所示。由仿真曲线可以看出，滤波算法对位置、速度和加速度的估计较为精确；位置和速度的滤波过程收敛较快，对加速度的滤波过程在20s内实现收敛，且对于目标存在蛇形机动的情况具有较好的跟踪效果。

对目标加速度曲线进行分析，可知其符合幅值衰减的周期性运动规律。短周期内的加速度可用如下的正弦和函数近似描述：

其中，ai为振幅，bi为频率，ci为每个基波的初相，m为级数的项数。采用滤波器收敛后的估计值对加速度曲线拟合，为了达到理想拟合精度的同时简化计算复杂度，利用双正弦和函数逼近临近目标加速度曲线，形式如下：

f(t)=a1sin(b1t+c1)+a2sin(b2t+c2)

利用其预测X，Y和Z方向加速度曲线。在得到加速度预测值后，以跟踪滤波的最后时刻数据作为初值，利用常加速度模型即可递推得到目标轨迹的预测结果。误差曲线如图 5所示。

开始预测的第20s，40s，60s，80s，100s和120s目标轨迹预测误差如表 2所示。

表2 目标轨迹预测误差

5 结论

由仿真曲线可以看出融合singer模型的扩展卡尔曼滤波算法对位置的估计较为精确；对加速度的估计需要20s左右的收敛时间。利用跟踪数据进行弹道预测，轨迹预测误差随时间增加而增大，120s的预测误差为30.6km(3σ)。

由于目标的实际运动特性要复杂得多，采用轨迹预测存在较大的预测误差，这是临近空间高超声速目标弹道预测无法避免的问题。因此，需要雷达持续跟踪目标，实时更新模型，才能更有效提高预测精度。

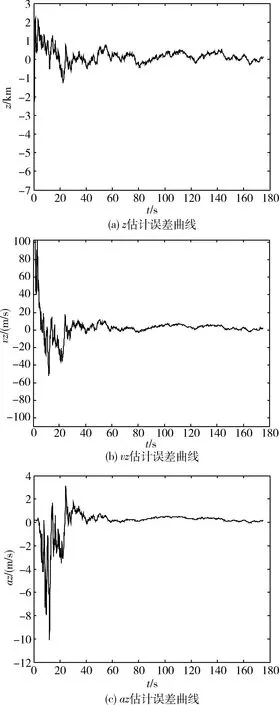
图4 z方向仿真曲线

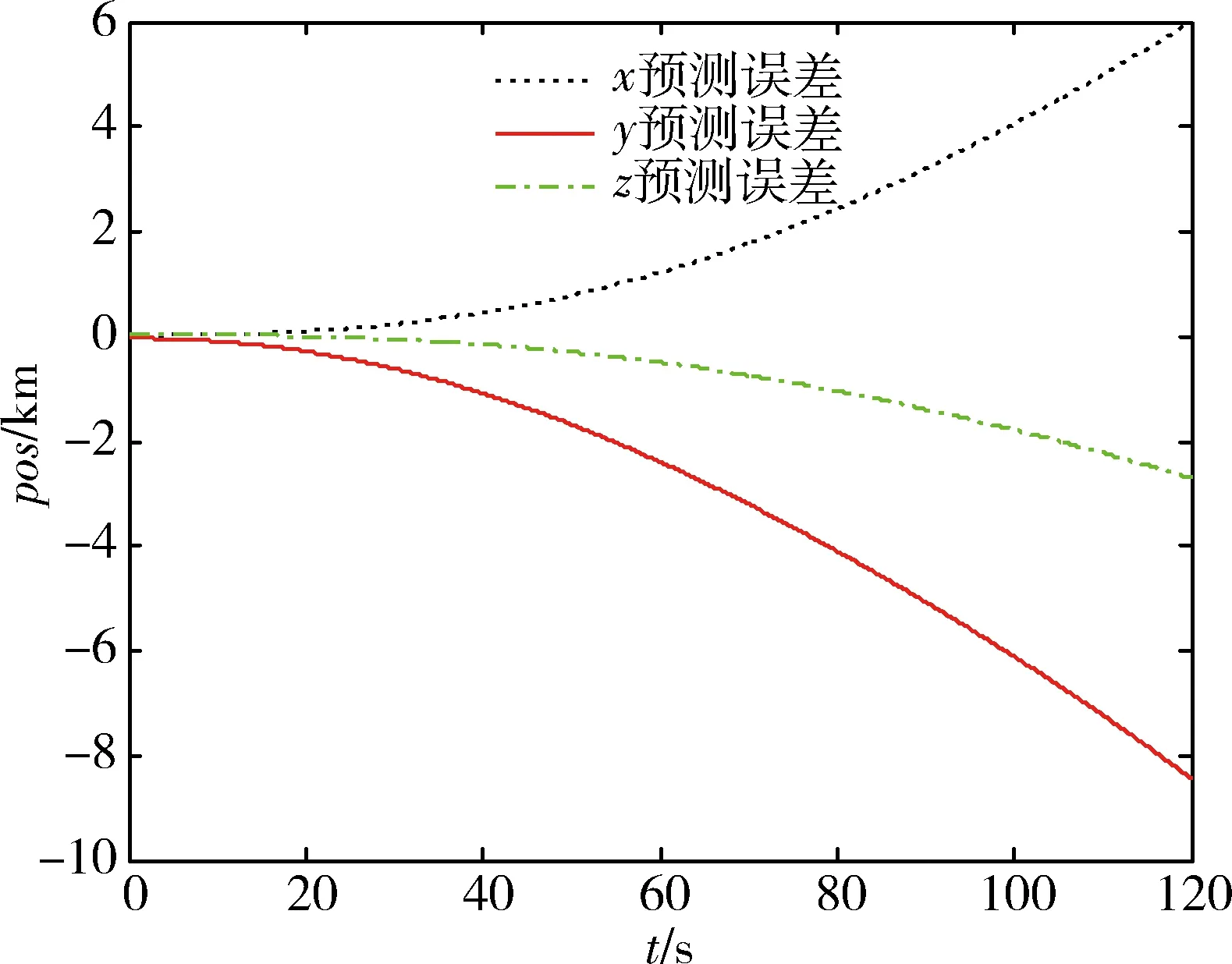
图5 轨迹预测误差曲线

[1] 张洪波, 谢愈, 陈克俊, 汤国建. 非惯性运动目标弹道预报技术探讨[J]. 现代防御, 2011, 39(6): 26-31. (Zhang H B, Xie Y, Chen K J, Tang G J. Investigation on Trajectory Prediction of Maneuverable Target[J]. Modern Defence Technology, 2011, 39(6): 26-31.)

[2] 王路, 邢清华, 毛艺帆. 助推-滑翔无动力跳跃飞行器轨迹预测[J]. 空军工程大学学报, 2015, 16(1): 24-27.(Wang L, Xing Q H, Mao Y F. A Track Forecasting Algorithm of Boost-Glide Unpropulsive Skipping Vehicle[J]. Journal of Airforce Engineering University, 2015, 16(1): 24-27.)

[3] 李昌玺, 毕红葵, 张兵, 肖松. 一种改进的高超声速目标跟踪算法[J].空军工程大学, 2012, 13(5): 50-54. (Li C X, Bi H Q, Zhang B, Xiao S. An Improved Tracking Algorithm for Hypersonic Targets[J]. Journal of Airforce Engineering University, 2012, 13(5): 50-54.)

[4] 秦雷, 李君龙, 周荻. 临近空间非弹道式目标HTV-2跟踪滤波与预报问题[J]. 航天控制, 2015, 33(2): 56-61.(Qin L, Li J L, Zhou D. The Problems of Tracking Filter and Prediction for Non-Ballistic Target HTV-2 in The Near Space[J]. Aerospace Control, 2012, 13(5): 50-54.)

[5] 雍恩米, 唐国金, 陈磊. 高超声速无动力远程滑翔飞行器多约束条件下的轨迹快速生成[J]. 宇航学报, 2008, 29(1): 46-51.(Yong E M, Tang G J, Chen L. Rapid Trajectory Planning for Hypersonic Unpowered Long-Range Reentry Vehicle with Multi-constraints[J]. Journal of Astronautics, 2008, 29(1): 46-51.)

[6] Li X R, Jilkov V P. Survey of Maneuvering Target Tracking: Part I. Dynamic Models[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1933-1964.

[7] 邓自立. 自校正滤波理论及其应用: 现代时间序列分析方法 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2003: 161-192.(Deng Z L. Self-tuning Filtering Theory and its Applications: Modern Time Series Analysis Method[M]. Harbin: Harbin Institute of Technology Press, 2003: 161-192.)

[8] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991: 10-24.(Zhou H R, Jing Z L, Wang P D. Maneuvering Target Tracking[M]. Beijing: National Defence Industry Press, 2003: 161-192.)[9] Zarchan P. Tactical and Strategic Missile Guidance [M]. Reston：Progress in Aeronautics and Astronautics, 2012: 439-471.

[10] 刘毅．自适应交互式多模型滤波在被动制导中的应用[J]．现代防御技术, 2009, 37(2): 41-45．(Liu Y. Adaptive Interacting Multiple Model Filter and Its Application in Passive Guidance[J]. Modern Defence Technology, 2012: 439-471.)

[11] Crassidis J, Junkins J. Optimal Estimation of Dynamic Systems [M]. Boca Raton: Chapman amp; Hall, 2004: 419-433.

[12] Kim S G，Crassidis J L，Cheng Y，et al. Kalman Filtering for Relative Spacecraft Attitude and Position Estimation [J]. Journal of Guidance, Control, and Dynamics. 2007, 30(1): 133-143.

[13] Goddard J S. Pose and Motion Estimation Using Dual Quaternion-based Extended Kalman Filtering [D]. Tennessee: The University of Tennessee,1997: 189-200.

TrajectoryTrackingandPredictionofHypersonicVehicleBasedonSingerModel

Wei Xiqing, Gu Longfei, Li Ruikang, Wang Sheyang

Shanghai Electro-Mechanical Engineering Institute, Shanghai 201109，China

Trajectorypredictionisthecriticaltechnologyforhypersonicvehicleinterceptorstoguidemissiletopredictiveimpactpointwithloweroverloadrequirement.TheextendedKalmanfiltercombinedwithSingermodelisproposedtoestimatenon-ballistichypersonictargetmotioninwhichtrajectoryhascharacterizedbycyclicjumpmotion.Trajectoryofhypersonicvehicleispredictedbyfittingaccelerationwithsumofsinefunctionsbyusingfiltereddata.Theexperimentresultsshowthatfairlygoodperformanceisachievedfortrajectorytrackingandprediction.

Hypersonicvehicle;Adaptive;Tracking;Trajectoryprediction

V448.2

A

1006-3242(2017)04-0062-05

2016-04-21

魏喜庆(1982-)，男，黑龙江鹤岗人，博士，高级工程师，主要研究方向为飞行器制导控制、非线性滤波；顾龙飞(1986-)，男，安徽马鞍山人，硕士，工程师，主要研究方向为飞行器制导控制；李瑞康(1982-)，男，江西瑞金人，博士，高级工程师，主要研究方向为飞行器制导控制；王社阳(1979-)，男，山西运城人，博士，研究员，主要研究方向为战术武器系统总体。