基于结构奇异值的不确定系统鲁棒性分析与评估

张亚婷 张惠平 郑总准 路坤锋

北京航天自动控制研究所，北京100854

基于结构奇异值的不确定系统鲁棒性分析与评估

张亚婷 张惠平 郑总准 路坤锋

北京航天自动控制研究所，北京100854

针对存在含有不确定性摄动的飞行器，提出一种基于结构奇异值的鲁棒性分析与评估方法。通过分析飞行器控制系统的不确定性摄动，基于线性分式变换方法，推导了飞行器不确定性摄动模型；基于μ分析方法，设计了一种控制律分析评估方法。并在系统鲁棒稳定的基础上，基于结构奇异值理论，分析了多输入多输出的不确定系统稳定裕度的计算方法。仿真结果表明，该方法有效保障了不确定性摄动系统控制律的鲁棒稳定性。

不确定系统；结构奇异值；控制律评估；鲁棒稳定性

新一代飞行器将在全空域全速域长时间飞行，未知的新环境存在更强的不确定性和更复杂的干扰因素，飞行器模型参数将大范围快速变化，同时通道间强烈交叉耦合，给控制系统的分析与评估带来了新的挑战。

通道间强烈的交叉耦合与飞行环境干扰因素的不确定，使控制系统表现为一个多输入多输出(MIMO)问题，必须寻求多变量系统稳定性判据分析系统稳定性。同时，气动参数、重心位置、质量、惯性矩和大气数据等的不确定造成了飞行器模型的不确定，这要求设计的控制律具有一定的鲁棒性。

结构奇异值是分析不确定系统鲁棒稳定性和性能的有效方法[1-3]，本文在描述飞行器控制系统不确定性的基础上，建立了一种基于结构奇异值的多变量稳定性判据，并进一步分析与评估系统控制律的有效性，为飞行器的稳定飞行提供理论依据。

1 系统不确定性分析与建模

控制系统的不确定因素分为2大类：模型不确定因素、与模型无关的不确定因素。其中模型不确定因素通常包括气动参数、重心位置、质量、惯性力矩、传感系统动态和大气数据等，可以归纳为惯性因素、气动参数、硬件变化及大气数据4种；与模型无关的不确定因素主要为通道间的交叉耦合等。上述不确定因素均可以使用数学方法建模描述。

线性分式变换(LFT)作为描述系统结构特征的有力工具，较好地解决了系统结构模型的问题，可以将所有不确定参数分离出来，使系统表达为一个标称模型加一个反馈的形式，如图1所示，其中飞行器模型为G，设计的控制器为K，不确定性为矩阵Δ，G与K组成标称模型。

图1 LFT结构框图

(1)

飞行器线性化数学模型如式(2)，模型系数中包含了惯性不确定、气动参数不确定、大气数据不确定及通道间交叉耦合影响。

(2)

按照飞行器的设计要求，将设计的控制律加入上述模型，则系统可表示为状态空间方程形式，如式(3)，其中：Ad(Δ)，Bd(Δ)，Cd(Δ)，Dd(Δ)为包含控制环节与不确定摄动的模型矩阵，Δ为不确定性矩阵。

(3)

进一步，将模型参数中不确定性摄动分离出来，考虑一种模型的仿射近似方案，如式(4)

(4)

为得到LFT模型，将摄动矩阵进行满质分解：

(5)

结合式(4)和(5)，得到不确定系统的LFT表达式为SΔ=Fu(M,ΔN)，其中：

(6)

2 控制律评估

线性分式变换模型将所有影响系统的不确定性构成一个不确定性矩阵Δ，这个矩阵具有对角或块对角形式，结合式(6)，则此时LFT系统SΔ=Fu(M,ΔN)的结构奇异值为：

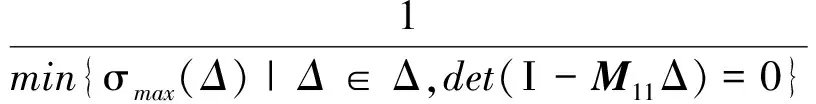
(7)

在不确定性的影响下，如果系统有一个极点逼近虚轴，μ的值就会迅速变大，理论上当极点刚好位于虚轴之上时，μ值等于1。因此，飞行器在不确定性摄动影响下，控制律评估步骤为：

1)在飞行特征点处，使用标称模型设计控制律；

2)考虑全部不确定性摄动的影响，将包含不确定性因素的飞行器模型描述为LFT形式；

3)沿s平面内的虚轴s=jω随频率的变化计算LFT的结构奇异值，判断μlt;1是否满足，满足则此特征点处控制律能够保障飞行器在不确定摄动影响下稳定飞行；不满足则返回重新设计控制律。

在所有特征点处计算LFT的结构奇异值，若μmaxlt;1均成立，则系统在不确定摄动的影响下鲁棒稳定，控制律能够保障稳定飞行。

3 稳定裕度计算

在系统鲁棒稳定的基础上，可以进一步分析计算不确定系统的稳定裕度。借鉴回差矩阵奇异值稳定裕度分析方法[4-5]的思路，令测量矩阵E=I+Δ，E=diag{k1ejφ1,k2ejφ2，…}，Δ为对角复数不确定摄动矩阵，Δ=diag{δ1,δ2，…}，加入测量矩阵的LFT系统模型如图2所示。当测量矩阵kmin≤ki≤kmax，闭环系统稳定时，系统幅值裕度为(kmin,kmax)；当φmin≤φi≤φmax，闭环系统稳定时，多回路系统的相角裕度为(φmin,φmax)。

图2 加入测量矩阵的线性分式系统

LFT模型中矩阵M∈Cn×n的结构奇异值μ定义为：

(8)

若Δ是空集，则定义μΔ(M)=0。μΔ(M)的倒数解释为LFT反馈系统稳定裕度的上确界，也就是导致反馈系统失稳的最小摄动的一个度量。

由于Δ=diag(kicosφi+jkisinφi-1)，结合μ的定义，若MIMO系统的μ≤β，即β=μmax，则Δ对角矩阵的每个对角元素的幅值小于等于β-1时，系统保持稳定。由于对角矩阵的最大奇异值就是其对角元素的最大幅值，因此有：

(9)

根据式(9)，取纵坐标为系统结构奇异值，横坐标为ki，对于不同的φi可以得到一组曲线，图3为结构奇异值最大值β与幅值-相位裕度的估计图，可以确定多变量控制系统幅值-相位同时变化时系统的稳定裕度。

图3 通用μ与幅值-相位裕度图

基于结构奇异值计算幅值裕度时，令φi=0；计算相位裕度时，令ki=1，则由式(9)可得多变量系统稳定裕度为：

(10)

4 仿真结果

某飞行器采用过载控制方式，输出为三通道过载偏差与弹体系角速度偏差，特征点处设计的控制矩阵为：

在标称系统的基础上，考虑惯性不确定、气动参数不确定、大气数据不确定及通道间交叉耦合影响，将控制律加入系统模型，计算参数摄动下LFT模型的结构奇异值，可得：当ω=[0.001, 20]时，此特征点在不确定参数摄动影响下的LFT模型结构奇异值曲线如图4所示，则系统存在不确定性参数摄动的情况下，μ值均小于1，即系统鲁棒稳定，所设计的控制律可以保障飞行器在存在不确定参数影响下稳定飞行。

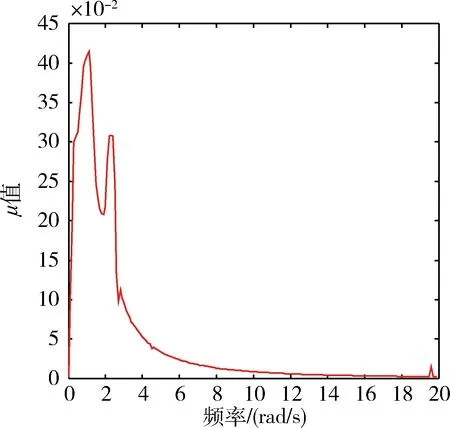
图4 参数摄动LFT模型奇异值曲线

标称系统结构奇异值曲线如图5所示，最大值为μ=2.78，由式(10)可得MIMO系统稳定裕度为：当系统增益和相位同时变化时，稳定裕度范围由图3确定；系统相位不变时，允许增益发生变化的最大范围为-8.9168dB～6.1455dB；系统幅值保持不变，允许相位发生变化的最大范围为：-20.7228°～20.7228°。

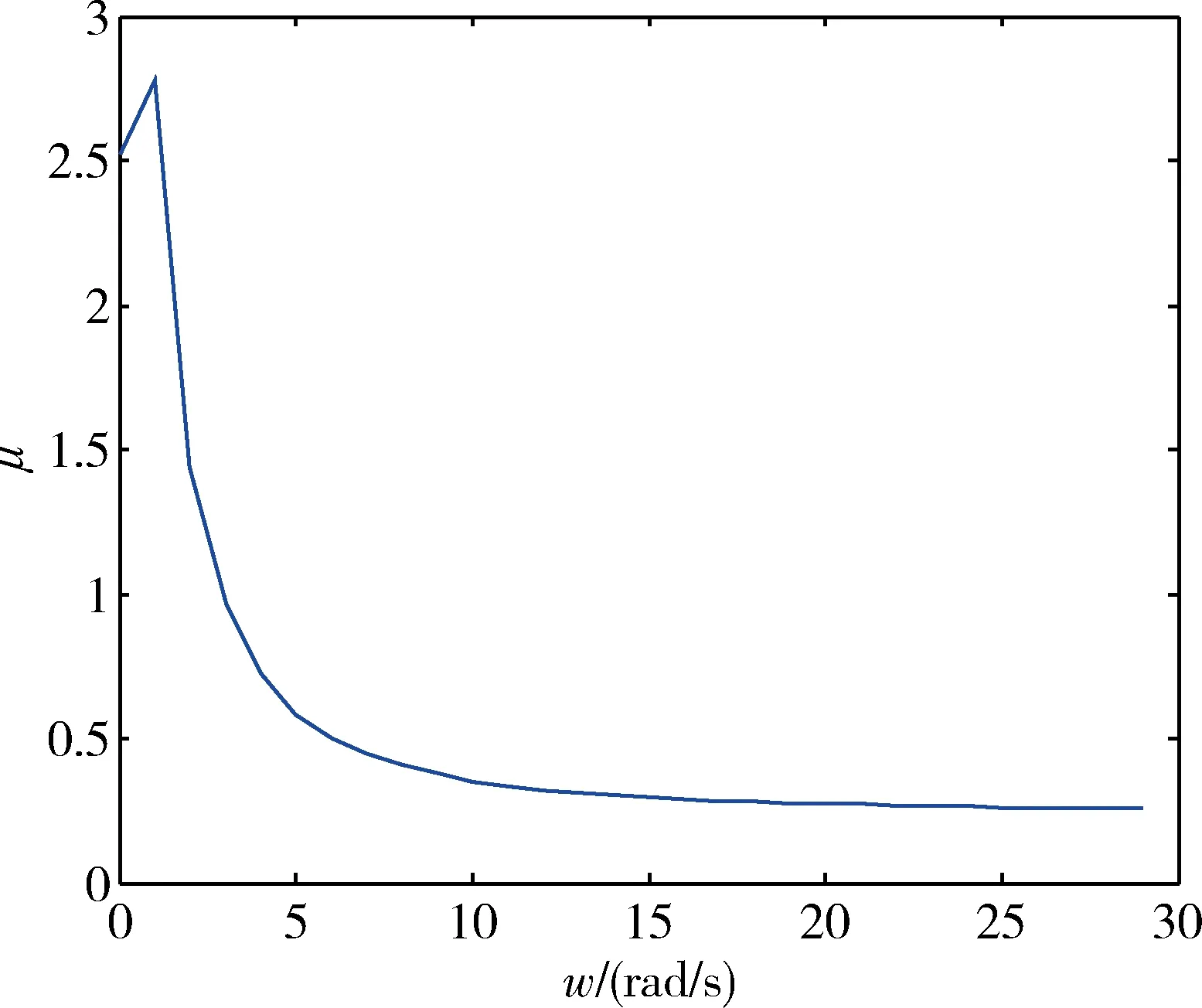
图5 标称系统结构奇异值曲线

应用控制律评估方法，对飞行器进行反复设计后，模型中加入惯性偏差、气动偏差和大气数据偏差等，仿真结果如图6～8所示。俯仰、偏航通道采用过载控制方法，加入偏差后，设计的控制参数能适应飞行器状态变化带来的影响，在摄动的影响下，控制系统能很好的跟踪制导过载指令，整个飞行过程比较平稳，控制律设计结果理想。

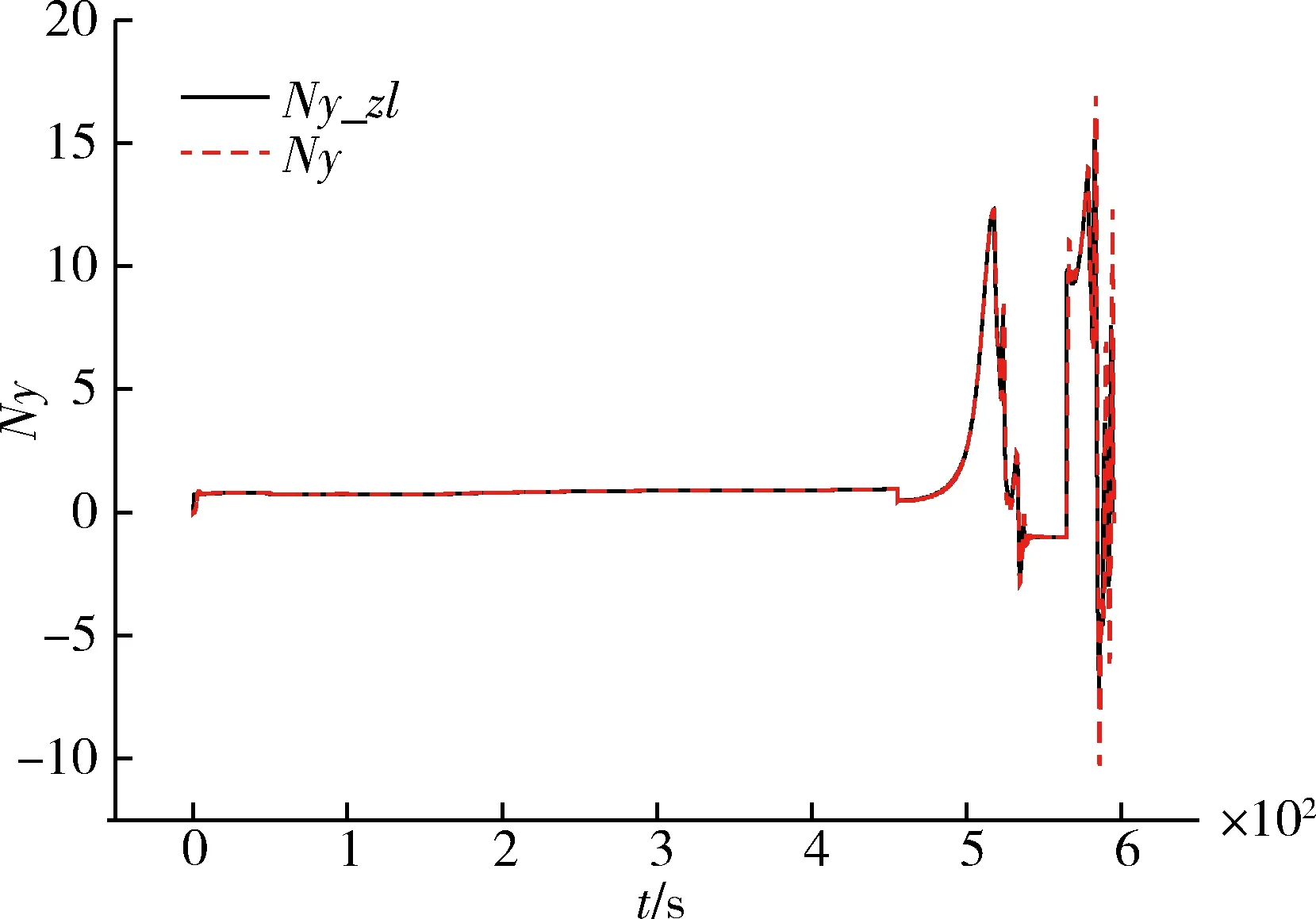
图6 法向过载曲线

图7 横向过载曲线

图8 角速度曲线

5 结论

针对含有不确定性摄动的飞行器控制系统，在线性分式变换与结构奇异值理论的基础上，提出了一种不确定性摄动影响下飞行器鲁棒稳定性分析与评估方法。仿真结果表明，基于结构奇异值的MIMO系统稳定性计算方法合理，基于μ分析的控制律评估方法能有效判断系统是否鲁棒稳定。同时，能计算多变量系统稳定裕度，可以为摄动系统的有效设计提供理论依据。下一步可以在模型辨识的基础上，研究飞行器控制律在线评估与自调整方法。

[1] Harald Pfifer, Simon Hecker. Generation of Optimal Linear Parametric Models for LFT-Based Robust Stability Analysis and Control Design[J]. IEEE Transactions on Control Systems Technology, 2011,19(1):118-131.

[2] Iordanov P I. Robust Analysis and Synthesis of Systems Subject to Parameter Uncertainty Using the Structured Singular Value[D]. Limerick: PhD Thesis, University of Limerick, 2003:20-62.

[3] Dimitry Gorinevsky, Gunter Stein. Structured Uncertainty Analysis of Robust Stability for Multidimensional Array Systems[J]. IEEE Transactions on Automatic Control, 2003,48(9):653-680.

[4] 李帆.不确定性系统的解耦控制与稳定裕度分析[D]．西安：西北工业大学博士学位论文,2001．(Li Fan. The Decoupling Control Study and Stability Margin Evaluation of Multivariable Uncertain Systems [D]. Xi’an: A Dissertation Submitted for the Degree of Ph.D of Northwestern Polytechnical University, 2001.)

[5] 吴斌，程鹏．多变量飞控系统的稳定裕度分析[J]．航空学报,1998,19(6):657-661．(Wu Bin, Cheng Peng. Stability Margin Analysis of the Multiloop Flight Control Systems [J]. Acta Aeronautica et Astronautica Sinica, 1998,19(6):657-661.)

RobustAnalysisandEvaluationofUncertainSystemsBasedonStructureSingularValue

Zhang Yating, Zhang Huiping, Zheng Zongzhun, Lu Kunfeng

Beijing Aerospace Automatic Control Institute, Beijing 100854, China

Accordingtotheaircraftinvolveduncertaintyperturbation,amethodofrobustanalysisandevaluationbasedonstructuresingularvalueisproposed.Themodelofuncertainsystemsisderivedbyanalyzinguncertaintyperturbationofaircraftcontrolsystemthroughthelinearfractionaltransformationmethod.Basedonμanalysismethod,amethodofcontrollawevaluationisdesigned.Andthestabilitymargincalculationmethodisanalyzedforuncertainsystemswithmultipleinputandmultipleoutputs,whichisbasedonthestructuresingularvalueprinciple.Thesimulationresultsshowthatthismethodcaneffectivelyguaranteetherobuststabilityofthecontrollawofuncertainsystem.

Uncertainsystem;Structuresingularvalue;Controllawevaluation;Robuststability

TJ765.2

A

1006-3242(2017)04-0011-04

2017-03-01

张亚婷(1989-)，女，陕西渭南人，硕士，助理工程师，主要研究方向为导航、制导与控制技术；张惠平(1979-)，男，宁夏固原人，硕士，研究员，主要研究方向为导航、制导与控制技术；郑总准(1983-)，男，福州人，博士，高级工程师，主要研究方向为导航、制导与控制技术；路坤锋(1983-)，男，石家庄人，博士，工程师，主要研究方向为导航、制导与控制技术。