备考与圆周运动相关的多过程问题——一浙江省高考物理试题为例

■浙江省龙湾中学 潘照萍

备考与圆周运动相关的多过程问题
——一浙江省高考物理试题为例

■浙江省龙湾中学 潘照萍

与圆周运动相关的多过程问题是近年来高考的热门考点之一,比如2016年高考全国Ⅰ卷理综第25题,2016年4月和10月浙江省新高考物理试题第20题都考查了与圆周运动相关的多过程问题。下面就以2016年浙江省新高考物理试题为例,谈谈与圆周运动相关的多过程问题的复习备考。

例题如图1所示,AB段是半径R=2L的四分之一圆形轨道,CDO段是半径r=L的半圆形轨道,半圆形轨道的最高点O处固定一个竖直挡板,小球碰到挡板后原速反向弹回,D为半圆形轨道的中点。两个轨道均光滑,如图连接固定。现将一个质量为m的小球从A点由静止释放,小球在竖直面内的轨道上运动。小球能不能到达半圆形轨道的最高点O位置?

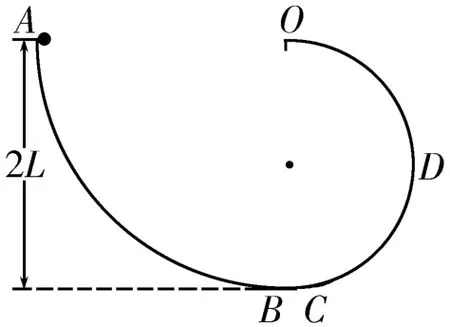
图1

解析:将小球从A点由静止释放,A与O点等高,如果不考虑小球脱离半圆形轨道,那么小球到达O点时的速度应恰好为零,但是小球恰好到达半圆形轨道最高点O的临界速度因此小球到达不了O点,而将会在半圆形轨道的DO段某处脱轨。

点拨:有的同学会误认为轨道光滑,A与O点等高,直接根据能量守恒定律判断小球到达O点时的速度恰好为零。这些同学错在没有考虑到小球在竖直面内圆形轨道上过最高点的临界条件。

变式1:如图2所示,将小球从A点的正上方距水平线OA高H处由静止释放,小球沿圆弧切线进入AB轨道,在竖直面内的轨道上运动,AB轨道粗糙,CDO轨道光滑。

问题1:当H=L时,小球恰好能够到达O点位置,求小球克服摩擦力做的功。

解析:选小球从初位置运动到O点为研究过程,由动能定理得

图2

点拨:求解小球克服摩擦力做的功,需要从功能关系的角度入手。

问题2:小球碰到挡板原速反向弹回后,能不能滑出A点?

解析:如果小球从A点滑到B点与小球反弹后从B点滑到A点的过程中克服摩擦力做功一样,那么小球刚好到达A点时的速度为零。小球在O点时的动能刚好等于小球在从A点滑到B点的过程中克服摩擦力做的功,即但是小球从A点滑到B点与小球反弹后从B点滑到A点的过程中克服摩擦力做功是不一样的。因为小球在轨道AB段上做圆周运动,需要向心力,根据能量守恒定律可知,小球反弹后从B点滑到A点比小球从A点滑到B点的过程中相同位置时的速度要小,所需的向心力就小,对应的摩擦力也小,摩擦力做功也少。因此小球滑到A点时的速度将大于零,即小球能够滑出A点。

点拨:小球在粗糙的AB轨道上运动时,受到的摩擦力大小与速度有关,这是一个难点。解这道题对我们深刻理解物体做圆周运动所需的向心力及物体克服摩擦力做的功很有帮助。

变式2:如图3所示,水平轨道BC与四分之一圆形轨道AB、半圆形轨道CDO平滑相连。已知H=1.4m,L=1m,m=1kg,小球与轨道BC间的动摩擦因数μ=0.4,小球与其他轨道间的摩擦忽略不计,取g=10m/s2。

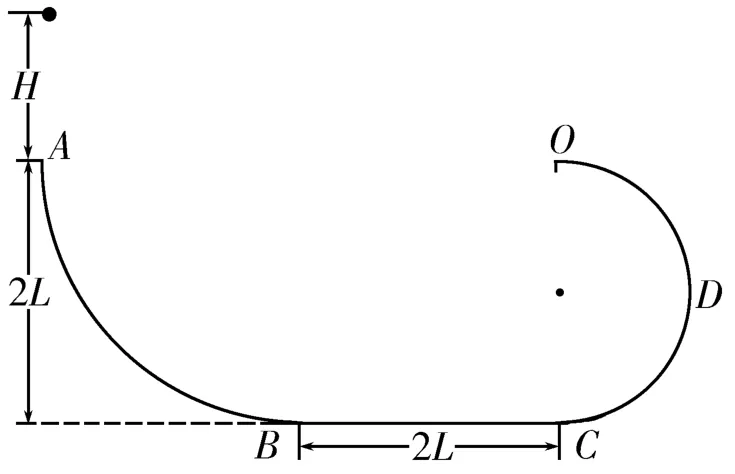
图3

问题1:小球第一次冲上轨道CDO,会不会脱轨?

解析:判断小球会不会脱离轨道CDO,需要看两个位置,即最高点O和半圆弧中间位置D点。如果小球能够到达O点或到不了D点,那么小球是不会脱轨的。如果小球能过D点,但是过不了O点,那么小球将在DO段某处脱轨。选小球从初位置运动到O点为研究过程,由动能定理得mgH-μmg·所以小球第一次冲上轨道CDO,不会脱轨。

问题2:小球全程会不会脱离轨道CDO?

解析:小球第一次到达O点,与竖直挡板碰后将原速反向弹回,计算出小球到达C点时的速度,就能够判断出小球会不会脱离轨道CDO。当小球恰好到达O点时,由解得当小球恰好到达D点(vD=0)时,由选小球从初位置运动到C点为研究过程,小球第二次冲上轨道CDO,要3次经过轨道BC,由mg(H+2L)-3μmg·2L=解得因此小球第二次冲上轨道CDO,到达D点时的速度为零,此后小球将沿轨道滑下并最终停在轨道BC上。小球全程将不会脱离轨道CDO。

点拨:在求解多过程问题时,如果我们不能一眼看出物体做往返运动的次数,那么可以一次一次地试探,直至找到其运动规律。

问题3:求小球在停止运动前,在水平轨道BC上经过的总路程。

解析:选小球从初位置到最终停止位置为研究过程,由mg(H+2L)-μmgs=0,解得s=8.5m。

问题4:小球最终静止时,到B点的距离是多少?

解析:因为小球在轨道BC上经过的总路程为8.5m,所以小球最终停在距离B点0.5m的位置。

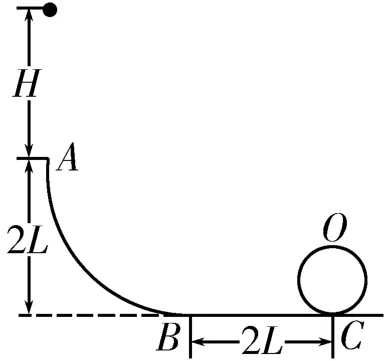
图4

变式3:如图4所示,将轨道CDO换成半径的螺旋圆形轨道CO,将小球与轨道BC间的动摩擦因数改为μ=0.8,小球与其他轨道间的摩擦忽略不计。

问题:若H=2L,且小球在轨道CO上运动时受到轨道的支持力不得超过其重力的9倍,试判断小球能否安全地通过轨道CO。

解析:判断小球能否安全地通过轨道CO,需要看两个位置,即轨道最高点O和最低点C。小球在轨道最低点C受到的支持力最大,最有可能超过其重力的9倍。选小球从初位置运动到C点为研究过程,由mg·所以小球能够过O点。由,解得N=10.6mg＞9mg,所以小球不能安全地通过轨道CO。

点拨:螺旋圆形轨道来自过山车模型,最低点C是错开的,只是没有画出来C'点。

变式4:在如图4所示轨道的基础上,依次与水平轨道CD、平滑轨道DE、半径的螺旋圆形轨道EF、平滑轨道EG平滑相连,如图5所示。轨道CD的长度为L,小球与轨道BC、CD间的动摩擦因数均为μ=0.8,不计小球与其他轨道间的摩擦,且轨道EF的最高点F与D、G两点等高。

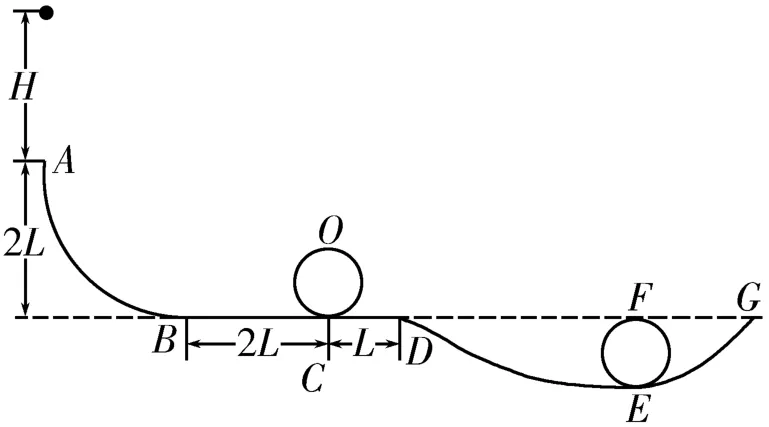
图5

问题:若H=2L,求小球过F点时对轨道的压力。

解析:因为圆形轨道EF的最高点F与D、G两点等高,所以vD=vF。选小球从初位置运动到D点为研究过程,由动能定理得解得,解得N=5.4mg。根据牛顿第三定律可知,小球在F点对轨道的压力为5.4mg,方向竖直向上。

变式5:在如图5所示轨道的基础上,再平滑地连上一段粗糙的斜面轨道GK,光滑的水平轨道KJ与轨道GK平滑连接,J端固定一根轻弹簧,如图6所示。斜面轨道的水平距离为与小球间的动摩擦因数也为0.8。不计小球在衔接点的能量损耗。

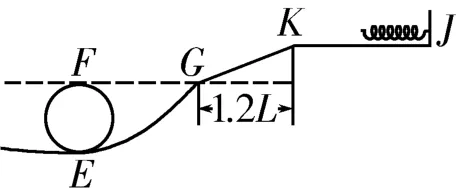
图6

问题1:若H=2L,小球能顺利滑上轨道GK,并平滑地滑上轨道KJ,求弹簧的最大弹性势能。

解析:因为D、F、G三点等高,所以vD=vF=vG。取小球从初位置运动到K点为研究过程,由动能定理得μmg·4.2L=Ek,解得Ek=0.14mg。小球在压缩弹簧时,弹簧的最大弹性势能等于小球在K点时的动能,即Ep=Ek=0.14mg。

点拨:引入一根轻弹簧,考查弹性势能等知识的题目在各地各类试题中经常出现。例如2016年高考全国Ⅰ卷理综第25题,2016年4月浙江省新高考物理试题第20题等。

问题2:小球经弹簧反弹后,平滑地通过K点,沿斜面轨道KG下滑,小球最终会不会停在斜面轨道KG上?若会,试求小球最终停在距离平面KJ多高的位置处。

解析:选小球从K点下滑到停在斜面上的位置为研究过程,设小球最终停在距离平面KJ的高度为h的位置处,由动能定理得

点拨:在与圆周运动相关的多过程问题中引入斜面模型,这在2016年浙江省新高考物理试题中连续两次都考到。其他省份的同学们也应该留意此类问题。

学习建议:与圆周运动相关的多过程问题,其实就是几个运动过程的拼接。同学们只要把直线运动、圆周运动和平抛运动等分别理清楚,就不会惧怕这类题目。同学们可以有针对性地整理一下往返运动、螺旋圆形轨道和斜面模型遵循的运动规律。对于竖直圆形轨道,一般会考查最高点和最低点的受力情况。另外,物体在竖直圆形轨道上的脱轨问题是难点,小球如果脱离轨道,肯定是在四分之一圆弧位置到最高点这段圆弧脱轨,我们可以把这段圆弧叫危险地带,把其余四分之三圆弧叫安全地带,如图7所示。

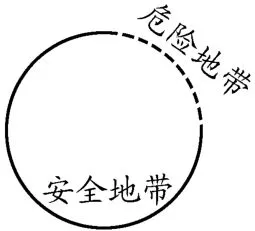
图7

(责任编辑 张 巧)