深度剖析牛顿第二定律的瞬时性

■湖北省武汉市黄陂区第一中学 李 辰

深度剖析牛顿第二定律的瞬时性

■湖北省武汉市黄陂区第一中学 李 辰

牛顿第二定律是解决力学问题的基础,也是历年高考的必考内容之一。它具有矢量性、同时性、瞬时性、独立性等特点。同学们在平时的习题练习中,往往会因为对“瞬时性”的理解不够深刻、掌握不够熟练而导致各种错误的出现。下面我们就来辨析一下这个容易让人感觉疑惑的“瞬时性”问题。

一、牛顿第二定律“瞬时性”的含义

根据牛顿第二定律可知,对于质量确定的物体而言,其加速度的大小和方向完全由物体受到的合外力的大小和方向所决定。物体的加速度和所受的合外力是瞬时对应关系,即同时产生、同时变化、同时消失,保持一一对应关系。

二、牛顿第二定律“瞬时性”的应用

1.在应用牛顿第二定律求解涉及弹簧或橡皮条类问题时,要根据弹簧或橡皮条的形变是连续的,导致其弹力的变化也是连续的这个特点,分析力在连续变化过程中的瞬时性。另外,还需要注意的是弹簧和橡皮条的弹力的大小和形变量有关,而且恢复原状需要较长的时间,从而致使其弹力不能突变。

2.在应用牛顿第二定律求解涉及刚性绳或接触面类问题时,要根据刚性绳或接触面的形变不需要时间,导致其弹力可以突变(变成零或其他值)这个特点,分析力在突然变化过程中的瞬时性。

例题如图1所示,天花板上用细绳吊起两个通过轻弹簧相连的质量相同的小球A、B,两小球均保持静止。当突然剪断细绳时,小球A与小球B的加速度分别为( )。

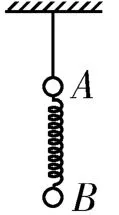
图1

A.a1=g,a2=gB.a1=2g,a2=g

C.a1=2g,a2=0 D.a1=0,a2=g

错解:剪断细绳时,以由小球A、B组成的系统为研究对象,系统只受重力作用,所以系统的加速度为g,即小球A、B的加速度均为g。答案为A。

错因分析:根据细绳和弹簧具有的不同特点可知,剪断细绳的瞬间,细绳对小球A的拉力突然消失,弹簧对小球A和B的作用力均不发生突变。因此,在细绳被剪断的瞬间,小球A和B的受力不同,具有的加速度自然也不相同,不能作为一个整体进行研究。

正解:分别以小球A、B为研究对象,它们在剪断细绳前的受力情况如图2所示。剪断细绳前小球A、B静止,小球A受细绳拉力T、重力mg和弹簧弹力F三个力作用,小球B受重力mg和弹簧弹力F'两个力作用。对小球A有T-mg-F=0,对小球B有F'-mg=0,又有F'=F,解得T=2mg,F=mg。剪断细绳时,细绳的拉力瞬间消失,而弹簧的形状不可瞬间改变,弹力还存在。因此,剪断细绳时,小球A受重力mg和弹簧弹力F两个力作用,小球B受重力mg和弹簧弹力F'两个力作用。对小球A有-mg-F=maA,对小球B有F'-mg=maB,解得aA=-2g(方向向下),aB=0。答案为C。

小结:牛顿第二定律反映的是力与加速度的瞬时对应关系。合外力不变,加速度不变;合外力瞬间改变,加速度瞬间改变。本题中在剪断细绳瞬间,小球A所受的合外力变化,加速度就由0变为2g,小球B所受的合外力不变,加速度不变。

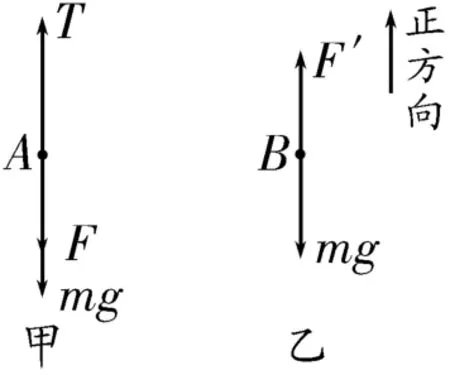
图2

跟踪训练

1.如图3所示,自由下落的小球下落一段时间后,与弹簧接触,从它接触弹簧开始到将弹簧压缩到最短,以下说法正确的是( )。

图3

A.小球刚接触弹簧瞬间,它的速度最大

B.从小球接触弹簧开始,它的加速度变为竖直向上

C.从小球接触弹簧到它运动至最低点,小球的速度先增大后减小

D.从小球接触弹簧到它运动至最低点,小球的加速度先减小后增大

2.如图4所示,物体甲、乙的质量均为m,弹簧和悬线的质量可以忽略不计。在悬线被烧断的瞬间,甲、乙两物体的加速度数值应是( )。

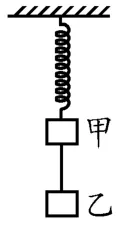
图4

A.0,gB.g,g

3.如图5所示,质量为m的小球用水平轻弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态。在木板AB突然向下撤离的瞬间,小球的加速度大小为( )。

图5

4.如图6甲所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,细线l1的另一端悬挂在天花板上,与竖直方向间的夹角为θ,细线l2水平拉直,物体处于平衡状态。

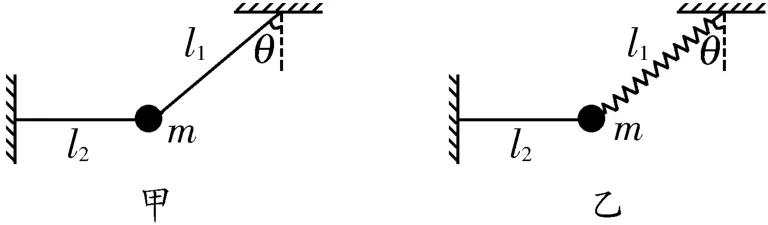
图6

(1)现将细线l2剪断,求剪断细线l2瞬间物体的加速度。

(2)若将细线l1改为长度相同、质量不计的弹簧,如图6乙所示,其他条件不变,求剪断细线l2瞬间物体的加速度。

参考答案:1.CD 2.B 3.A

4.(1)a=gsinθ,方向与细线l1垂直。(2)a'=gtanθ,方向水平向右。

(责任编辑 张 巧)