1 MW/60 MJ飞轮储能系统轴系动力学分析与试验研究
2017-11-24魏鲲鹏戴兴建
刘 佩,魏鲲鹏,戴兴建
1 MW/60 MJ飞轮储能系统轴系动力学分析与试验研究
刘 佩,魏鲲鹏,戴兴建
(清华大学工程物理系,北京100084)
为了解决钻机动力传动系统载荷波动大的问题,研制了1 MW/60 MJ飞轮储能系统实现动力调峰运行。分别采用传递矩阵法和有限元法对飞轮转子支承系统进行动力学建模,计算出飞轮轴系临界转速和振型;并使用有限元法对壳体等非转动部件建模并计算模态。进行飞轮升降速试验,实时监测降速过程中幅频特性和相频特性。对比数值仿真与试验结果一致,为飞轮储能系统的轴系设计与改进提供理论与试验依据。
飞轮储能系统;传递矩阵法;有限元法;模态分析
飞轮储能技术是通过电动/发电机将飞轮机械能与电能相互转化的技术,具有充电时间短、响应速度快、能量密度较高、使用寿命长、环保无污染等优点[1-2]。随着高强度复合材料、大功率电动/发电机、磁悬浮、真空和电力电子等技术的发展,飞轮储能技术目前已经在电网调频、电能质量控制、卫星储能/姿控、车辆制动能量回收、不间断电源和高功率脉冲电源等领域获得了广泛的应用[3-7]。近年来我国在飞轮储能关键技术方面有所突破,部分大学和科研机构已经完成飞轮储能系统试验装置或工程样机的研制[8-10]。
石油钻机的起、下钻工况中的载荷具有大幅度波动特性,飞轮储能系统的使用可以降低钻机动力功率配置[11]。在飞轮储能混合动力系统中,飞轮储能系统的工作方式是:钻机在下钻工况中,将下放钻具势能回收发电,供给飞轮储能系统以机械能形式存储;绞车启动提升时,飞轮储能系统将存储的机械能转化为电能,驱动混合动力系统的调峰电机,实现回收能量再利用。
本文以1 MW/60 MJ飞轮储能系统为研究对象,分析飞轮电机轴系的动力学特性以及机组外壳的动力学特性。分别使用传递矩阵法和有限元法对飞轮轴系进行动力学计算,分析其临界转速、振型等特性,并采用有限元法分析轴系和壳体振动模态。在飞轮储能系统充放电运行中,检测飞轮储能系统壳体振动,与动力学计算结果进行对比验证。
1 飞轮储能系统
飞轮储能系统要由飞轮、轴承、发电/电动 机、控制系统和机组外壳组成,其机械部分如图1所示。

图1 飞轮储能系统示意图
飞轮材料采用高强度合金钢,总质量5300 kg,极转动惯量1535 kg/m2,设计工作转速1200~2400 r/min,最高转速2700 r/min,总储能量60 MJ[12]。外壳等静止部件采用合金钢,总质量约3500 kg。
飞轮轴系上、下端使用滚动轴承作为径向支承,这是因为滚动轴承结构简单、可靠、易维护。飞轮轴系上端使用永磁轴承作为轴向支承,承担95%的转子重量,可大大降低轴承摩擦损耗。
电动/发电机定子部分安装在壳体上,其转子通过键槽结构固定于飞轮轴系上。
2 动力学计算
转子动力学主要包括计算临界转速和动力响应、分析稳定性、动平衡等内容。一般来说,转子系统的运动微分方程可以写为式(1)
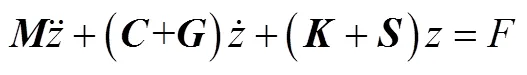
式中,是广义坐标矢量,是质量矩阵,是阻尼矩阵,是陀螺效应矩阵,是刚度矩阵对称部分,是刚度矩阵不对称部分,是广义外力。
考虑到实际问题需要求解的自由度数量较多,直接求取上述方程的特征值或响应是很困难的。实用的计算方法可以分为传递矩阵法和有限元法两大类,传递矩阵法状态向量的阶数确定,编程简单,运算速度快;有限元法表达式简洁、规范,模型更接近实际情况,随着计算工具运算能力的增强和成本的下降,在求解复杂系统问题时体现出较大优势。
2.1 传递矩阵法
飞轮电机轴系是质量连续分布的弹性体,其自由度有无穷多个。为了便于求解,选取轴的端部、轴颈中心、轴的截面突变处和飞轮中心为结点,如图2所示。使用集总质量法[13]沿轴线把转子质量及转动惯量集总到若干个结点上,各结点间通过无质量等截面的弹性轴段连接,将转子简化为具有若干个集总质量和集总转动惯量的模型。

图2 飞轮轴系简化示意图
传递矩阵法的计算原理:使用力学方法建立圆盘、轴段、支承等典型部件两端截面的状态矢量传递关系式,利用连续条件,建立转子任一截面状态向量与起始截面状态向量的传递关系,通过边界条件搜索满足剩余量条件的涡动频率,就可以得到转子的各阶临界转速[14]。
传递矩阵法中典型组合构件如图3所示,其传递矩阵为式(2)
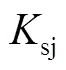
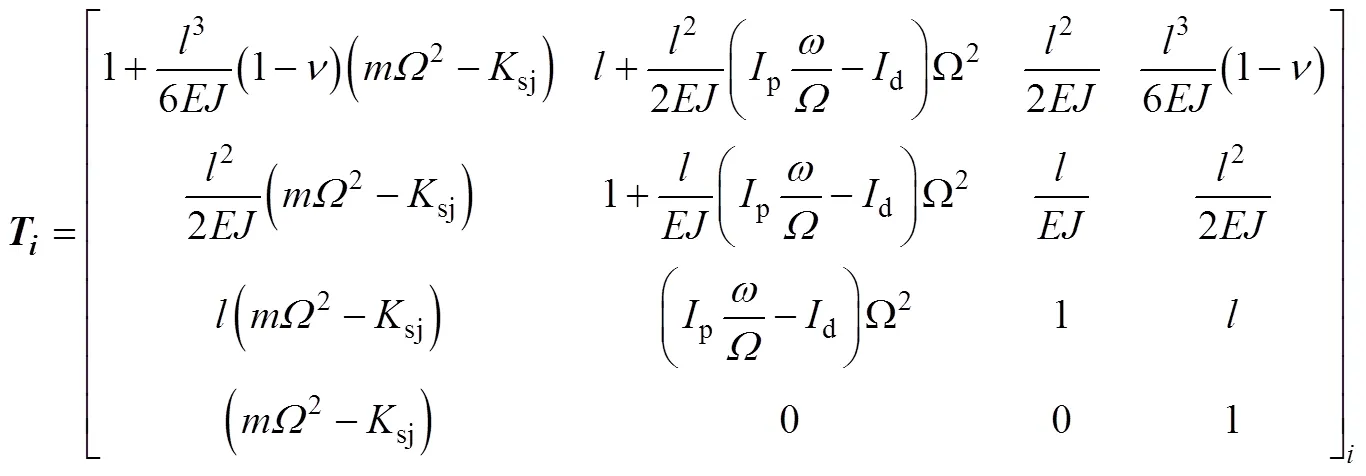
假设飞轮轴系的径向支承是各向同性而且不考虑阻尼,则弯曲振动时其挠曲线在同一平面,因此分析一个平面内的横向弯曲振动就可以得到轴系的临界转速和振型。
如图2所示,转子左、右两端均为自由端,取左端为起始截面。如表1所示,在飞轮储能电源工作范围内使用改进Riccati法[15]通过扫频计算得到不同支承刚度下转子的一阶、二阶临界频率。轴承刚度一般为5×107~2×109N/mm,包含轴承座刚度的轴系支承刚度计算范围取1×107~1×109N/m。刚度为1×108N/m时,绘制相应的剩余量曲线,如图4所示。
扫频范围为0~300 r/s,在此范围内轴系存在两个临界转速(表1)。求得临界转速后,可以得到起始截面状态矢量的比例解,通过转子任一截面状态向量与起始截面状态向量的传递关系,可求取各截面状态矢量的比例解,进而绘制对应振型,如图5所示。红、绿色曲线分别表示飞轮轴系一阶临界和二阶临界的振型图:一阶振型与0线没有交点,转子上端位移小,下端位移大;二阶振型与0线存在一个交点,交点位于大飞轮附近,转子上端位移大,下端位移小。
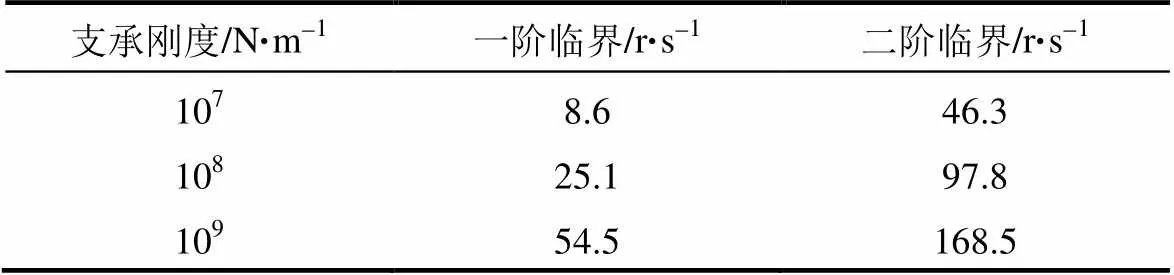
表1 临界转速计算
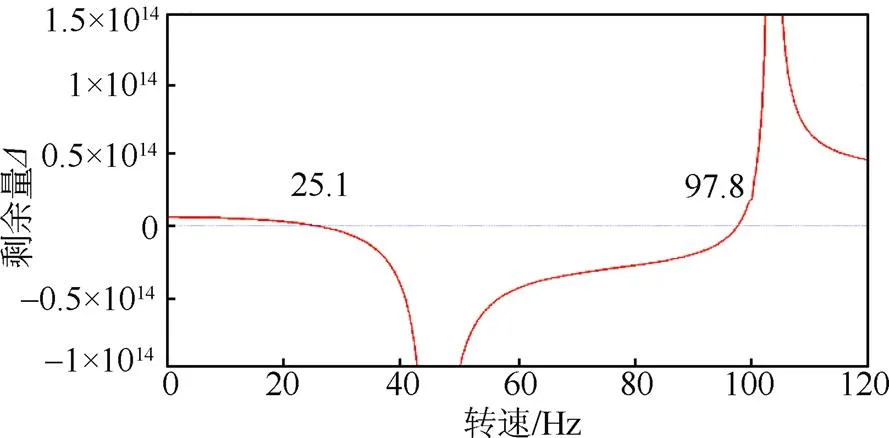
图4 剩余量曲线
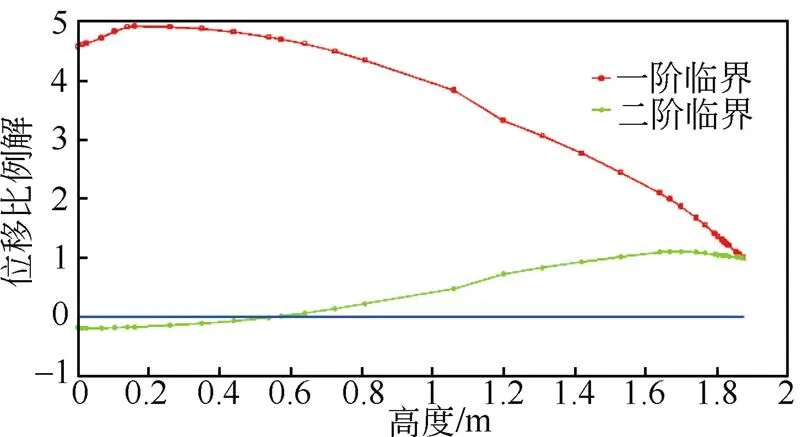
图5 临界频率振型图
2.2 有限元法
有限元法采用数值分析得到数值解,在满足工程需要的前提下模拟物理现象[16]。ANSYS求解需要将实体模型离散为有限元模型,选择合适的求解类型,分析计算结果并对模型进行修正和校验。
假设飞轮轴系为线性结构,进行模态分析。建立实体模型后使用可考虑陀螺效应的SOLID187实体单元对飞轮转子划分网格;使用COMBI214模拟支承特性。飞轮转子支承系统的有限元模型如图6所示,生成618818个节点,417246个单元。通过APDL 编程对轴系施加0~100 Hz转动频率,采用阻尼法提取前6阶模态频率与振型,并绘制坎贝尔图(图7),进而求得飞轮轴系的临界转速与振型。考虑实际工作情况,转子轴系自转与进动方向一致,因此正进动曲线与45°线的交点为临界转速。如表2所示,计算不同支承刚度下转子的一阶、二阶临界转速。
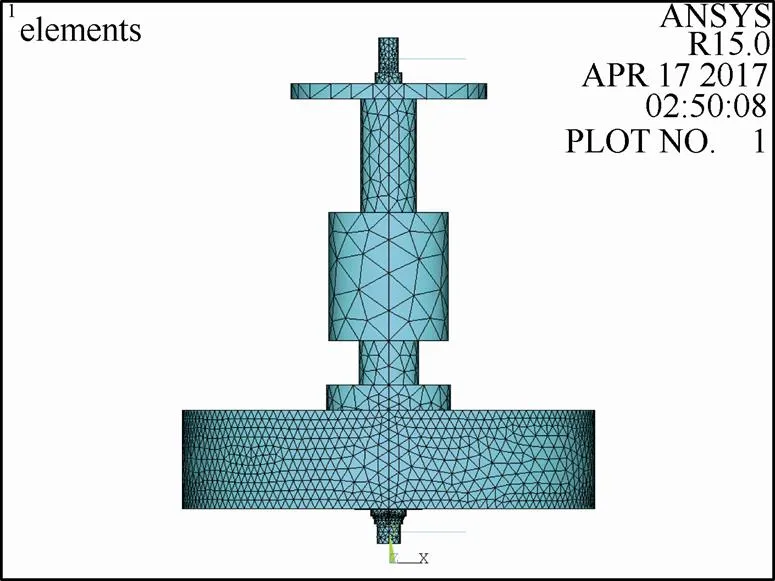
(a)
(b)
图6 飞轮轴系有限元模型
Fig.6 Finite element model of flywheel shafting
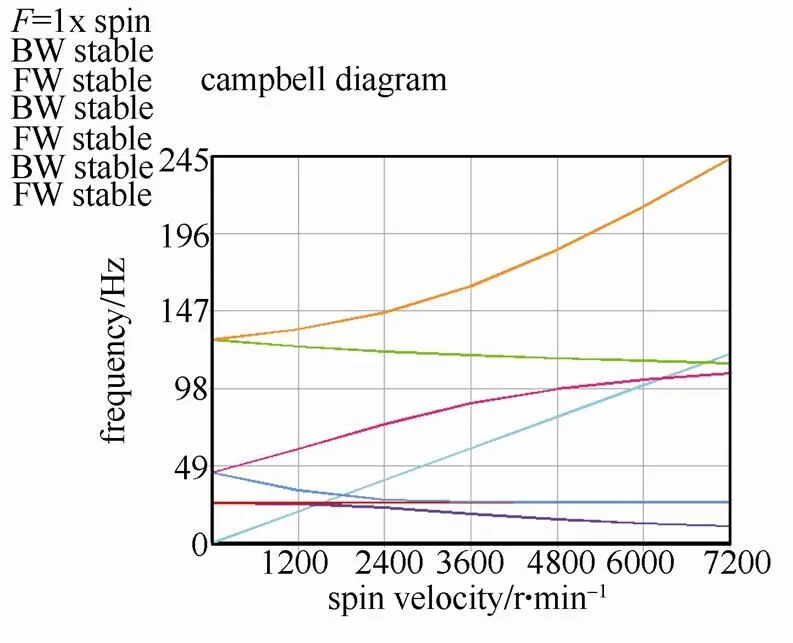
图7 飞轮轴系坎贝尔图
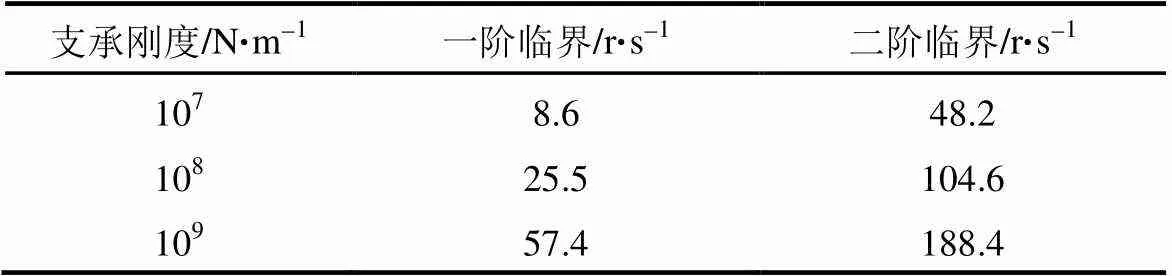
表2 临界转速计算
飞轮电机轴系一阶临界转速对应的振型与过飞轮轴线的剖面位移矢量如图8所示,观察剖面位移矢量图发现轴系上端位移小,下端位移大,飞轮振型与轴线没有交点,为平动模态。飞轮轴系二阶临界转速对应的振型与过飞轮轴线的剖面位移矢量如图9所示,观察剖面位移矢量图发现轴系上端位移大,下端位移小,飞轮振型与轴线存在一个交点,交点位于大飞轮上端,为摆动模态。
比较传递矩阵法和有限元法的计算结果,两者基本一致。

图8 飞轮轴系一阶临界振型

图9 飞轮轴系二阶临界振型
2.3 轴系和壳体的模态分析
飞轮电机轴系通过轴承安装在壳体上,旋转时激励壳体引发振动,因此需要对轴系和壳体建立有限元模型并提取模态。
使用SOLID187实体单元分别对轴系和壳体划分网格,使用COMBI214单元模拟轴系与壳体、壳体下端的支承特性,轴系上端轴向支承刚度设为1×109N/m,约束壳体底面所有自由度。建立轴系和壳体的有限元模型,生成1733386个节点,1134251个单元,如图10所示。
轴系非转动情况下,计算不同支承刚度下轴系和壳体的模态频率,如表3所示。

图10 轴系和壳体有限元模型

表3 模态频率计算
考虑到有限元模型为对称结构,将相同的频率合并为一个模态,则支承刚度为1×108N/m时,系统前3阶模态频率,分别为24.7 Hz、38.7 Hz、42.5 Hz,其模态振型分别如图11~图13所示。
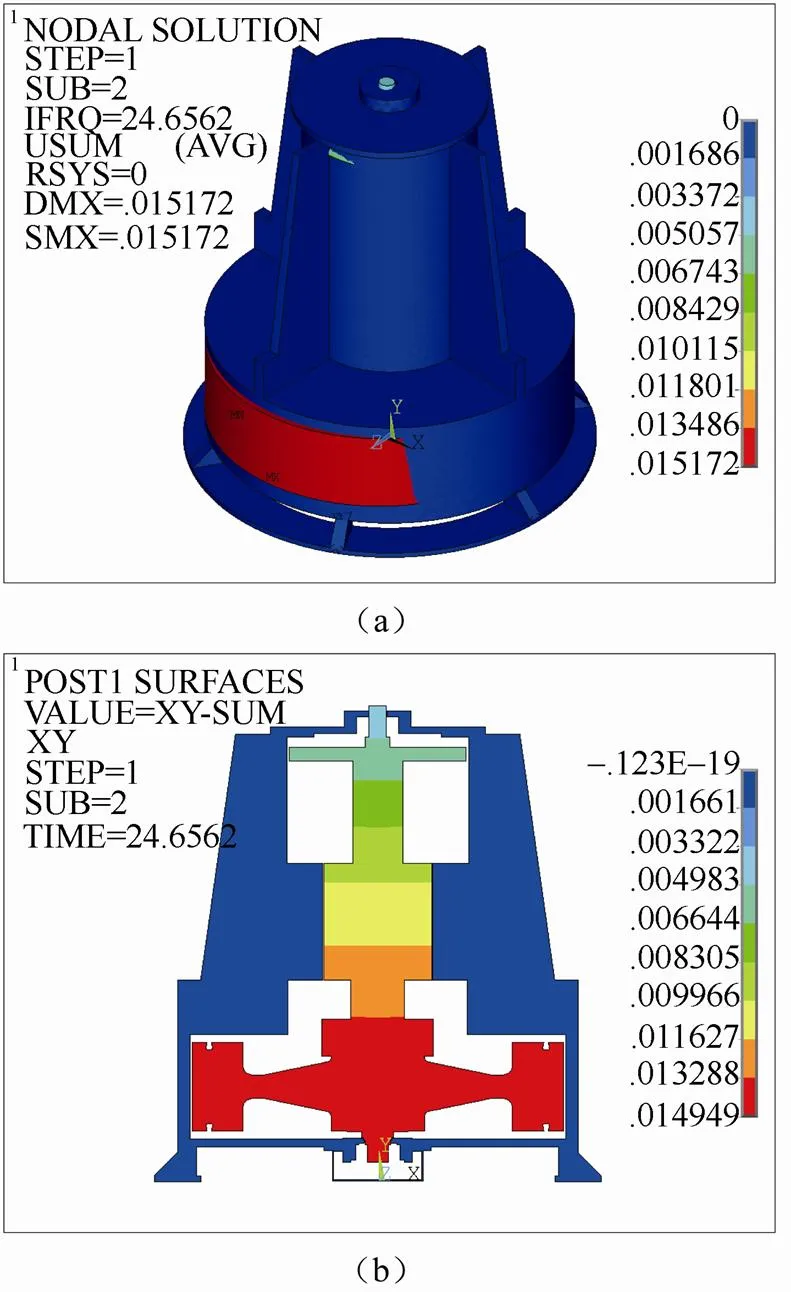
图11 一阶模态振型

图12 二阶模态振型
观察轴系和壳体的一阶模态振型,发现壳体位移与轴系相比较小,与壳体耦合计算轴系振型与单独计算的飞轮轴系一阶模态振型相似。
观察轴系和壳体的二阶模态振型,发现壳体位移与轴系相比较小,轴系位移整体较大,是由轴向支承引起的轴向振动。

图13 三阶模态振型
观察轴系和壳体的三阶模态振型,发现壳体位移与轴系相比较小,与壳体耦合计算的轴系振型与单独计算的飞轮轴系二阶模态振型相似。
3 试验研究
为掌握该飞轮储能系统的运行特性,验证动力学数值仿真结果,需通过升降速试验进行实时的振动测量。如图1所示,在壳体上端和壳体下端安装位移传感器测量壳体振动,通过测量数据了解飞轮储能系统轴系的振动状态。
检测两组飞轮储能系统降速过程中的幅频特性和相频特性(通过动平衡仪的同频分量检测),第一组为飞轮自2400 r/min降速至800 r/min处,第二组为飞轮自2100 r/min降速至200 r/min处,如图15所示。曲线A1、A2分别表示传感器A测得的第一组、第二组数据,B1、B2表示传感器B测得的第一组、第二组数据。
观察第一组实验数据,飞轮自2400 r/min降速至2100 r/min过程中,传感器A、B测得的振幅波动较小,相位基本同向且无明显改变。观察第二组实验数据,飞轮自750r/min降速至450 r/min过程中,传感器A、B测得的振幅随转速降低先增大后减小,期间两传感器的相位基本同向,530 r/min处振幅最大。
观察两组实验数据,飞轮自2100 r/min降速至1650 r/min过程中,传感器A、B测得振幅波动 较小,但是相位经历了同向-反向-同向过程。从 1650 r/min降速到1300 r/min过程中,传感器A、B测得振幅随转速降低先急剧增大后减小,且A处振幅远高于B处,相位经历了同向-反向-同向过程,表现出通过临界转速的特征,壳体的预测一阶模态频率(支承刚度取1×108N/m)位于此共振区间。
从1300 r/min降速到900 r/min时,传感器A、B测得振幅随转速降低先增大后减小,且A处振幅高于B处,相位基本同向。
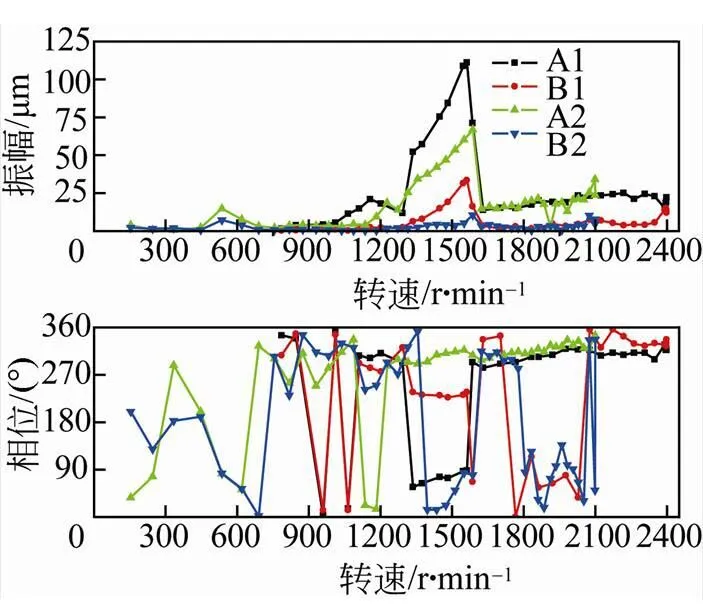
图14 幅频特性曲线
4 结 论
本文对1 MW /60 MJ飞轮储能系统轴系分别采用传递矩阵法和有限元法进行动力学建模,计算得到临界转速和振型;并用有限元法对非转动情况下轴系和壳体建有限元模型,提取了相应的模态频率与振型。
进行飞轮储能系统的充放电试验,实时检测飞轮降速过程的振动特性。在转速1300~1650 r/min内存在共振,试验结果与采用特定支承刚度计算预测结果一致。
进一步的研究包括支承刚度的理论和试验分 析方法,考虑使用合适的传感器直接测量轴系振动,更准确地了解轴系的振动特性,以便改进和优化 设计。
[1] SCHAINKER R B. Executive overview: Energy storage options for a sustainable energy future[C]//Power Engineering Society General Meeting. IEEE, 2004, 2: 2309-2314.
[2] BOLUND B, BERNHOFF H, LEIJON M. Flywheel energy and power storage systems[J]. Renewable & Sustainable Energy Reviews, 2007, 11(2): 235-258.
[3] ALEXANDER B X S. Rotor position and vibration control for aerospace flywheel energy storage devices and other vibration based devices[D]. USA: Dissertation Abstracts International, 2008.
[4] RAY P K, MOHANTY S R, KISHOR N. Frequency regulation of hybrid renewable energy system for large band wind speed variation[C]// International Conference on Power Systems, 2009: 1-6.
[5] MCKERAGHAN D. Flywheel energy storage—A UPS battery's best friend[J]. Battery Power Products & Technology Magazine, 2012, 6(3): 9.
[6] SUN X J, WANG X G, WANG D M. Research on the control of aircraft energy system based on flywheel battery[J]. Advanced Materials Research, 2013, (753/755): 2621-2627.
[7] TAJ T A, HASANIEN H M, ALOLAH A I, et al. Transient stability enhancement of a grid-connected wind farm using an adaptive neuro-fuzzy controlled-flywheel energy storage system[J]. Renewable Power Generation Iet, 2015, 9(7): 792-800.
[8] 戴兴建, 唐长亮, 张剀. 先进飞轮储能电源工程应用研究进展[J]. 电源技术, 2009, 33(11): 792-800.
DAI Xingjian, TANG Changliang, ZHANG Kai. Progress of advanced power system using flywheel energy storage[J]. Chinese Journal of Power Sources, 2009, 33(11): 792-800.
[9] 张维煜, 朱熀秋. 飞轮储能关键技术及其发展现状[J]. 电工技术学报, 2011, 26(7): 141-146.
ZHANG Weiyu, ZHU Huangqiu. Key technologies and development status of flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 141-146.
[10] 戴兴建, 邓占峰刘刚, 等. 大容量先进飞轮储能电源技术发展状况[J]. 电工技术学报, 2011, 26(7): 133-140.
DAI Xingjian, DENG Zhanfeng, LIU Gang, et al. Review on advanced flywheel energy storage system with large scale[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 133-140.
[11] 张超平, 戴兴建, 苏安平, 等. 石油钻机动力系统飞轮储能调峰试验研究[J]. 石油机械, 2013, 41(5): 3-6.
ZHANG Chaoping, DAI Xingjian, SU An’ping, et al. Experimental study of flywheel energy storage and peak regulation of rig power system[J]. China Petroleum Machinery, 2013, 41(5): 3-6.
[12] 汪勇, 戴兴建, 李振智. 60 MJ飞轮储能系统转子芯轴结构设 计[J]. 储能科学与技术, 2016, 5(4): 503-508.
WANG Yong, DAI Xingjian, LI Zhenzhi. Structural design of rotors and shafts of a 60 MJ flywheel energy storage system[J]. Energy Storage Science and Technology, 2016, 5(4): 503-508.
[13] 钟一谔, 何衍宋, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1987.
ZHONG Yi’e, HE Yanzong, WANG Zheng, et al. Rotordynamics[M]. Beijing: Tsinghua University Press, 1987.
[14] 闻邦春, 顾家柳, 夏松波. 高等转子的力学[M]. 北京: 机械工业出版社, 2000.
WEN Bangchun, GU Jialiu, XIA Songbo. Advanced rotordynamics[M]. Beijing: Mechanical Industry Press, 2000.
[15] 王正. Riccati传递矩阵法的奇点及其消除方法[J]. 振动与冲击, 1987(2): 77-81.
WANG Zheng. The elimination method for singularity of Riccati transfer matrix method[J]. Journal of Vibration and Shock, 1987(2): 77-81.
[16] 曾攀. 有限元分析及应用[M]. 北京: 清华大学出版社, 2004.
ZENG Pan. Finite element analysis and application[M]. Beijing: Tsinghua University Press, 2004.
Analysis and experimental study on the shaft of a 1MW / 60MJ flywheel energy storage system
LIU Pei, WEI Kunpeng, DAI Xingjian
(Department of Engineering Physics, Tsinghua University, Beijing 100084, China)
A 1 MW/60 MJ flywheel energy storage system was developed for smoothing load fluctuations of a drilling rig power system. This paper introduces the use of transfer matrix method and the finite element method to model the flywheel rotor-support system, and to calculate the critical speeds and vibration modes of the flywheel shaft. The finite element method was also used to calculate the modal frequency of protective casing of the system. An experimental study was performed on flywheel acceleration and deceleration processes to obtain real-time the amplitude-frequency characteristics. The numerical simulations were in agreement with the experimental results. The results provide basis for the design and improvement of flywheel energy storage systems.
flywheel energy storage system; transfer matrix method; finite element method; modal analysis
10.12028/j.issn.2095-4239.2017.0047
TH 133
A
2095-4239(2017)06-1257-07
2017-04-25;
2017-05-20。
国家科技支撑计划项目(2014BAA04B02)。
刘佩(1992—),男,硕士研究生,研究方向为飞轮储能系统转子动力学,E-mail:lp1033286826@163.com;
戴兴建,副研究员,研究方向为高速旋转机械及飞轮储能技术,E-mail:daixj@mail.tsinguahua.edu.cn。
