拟梯子的(2,1)-全标号

金 鑫，党雪娇，吕大梅

(南通大学 理学院，江苏 南通 226007)

拟梯子的(2,1)-全标号

金 鑫，党雪娇，吕大梅*

(南通大学 理学院，江苏 南通 226007)

图的一个(2,1)-全标号指的是从点集和边集到非负整数集的一个函数f，且使得：任两个相邻顶点标号相异；任两个相邻边标号相异；以及任两个关联的点和边标号差至少为2.本文研究了拟梯子的(2,1)-全标号,并完全确定了拟梯子的(2,1)-全标号数.

L(2,1)-标号;(2,1)-全标号；(2,1)-全标号数;拟梯子

0 引言

在通信波段分配问题的驱动下，诞生了距离2标号问题.Griggs和Robert[1]在此问题基础上，提出了图的L(2,1)-标号概念,并作了深入探讨，可见综述[2-4].

一个简单图G的L(2,1)-标号指的是从顶点集V(G)到非负整数集的一个函数f，且使得d(u,v)=1时,|f(u)-f(v)|≥2；当d(u,v)=2时，|f(u)-f(v)|≥1。不妨设最小标号为0。则图G所有L(2,1)-标号下的跨度max{f(v);v∈V(G)}的最小值就是G的L(2,1)-标号数，记为λ(G)。

1995年[5]，Whittlesty等对剖分图的L(2,1)-标号进行了研究。2002年[6-7]，Havet和Yu把剖分图的L(2,1)-标号称为图的(2,1)-全标号，并将之推广，进一步研究了图的(d,1)-全标号。接下来我们先给出(2,1)-全标号的定义。

一个图G的(2,1)-全标号指的是从点集及边集到非负整数集的一个函数f，且：任两相邻顶点标号相异；任两相邻边标号相异；以及任关联的点和边标号也相异。不妨设最小标号为0。则G所有(2,1)-全标号下的跨度max{f(v);v∈V(G)∪E(G)}的最小值为图G的(2,1)-全标号数，记为λT(G)。

文献[8-11]研究了拟梯子和拟Möbius梯子的一些标号.本文将研究拟梯子的(2,1)-全标号问题。下面我们给出拟梯子的定义。

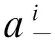
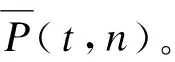
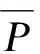
引理1.1[1]G是最大度为Δ≥2的图，则λ(G)≥Δ+1。

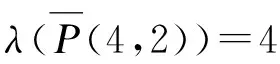
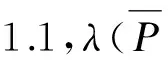
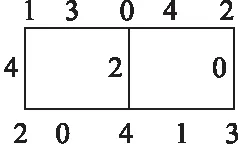
图1(a)

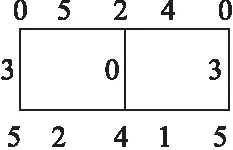
图1(b)

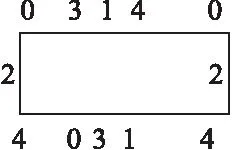
图2

图3

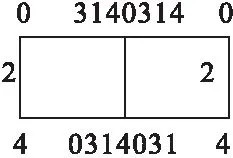
图4

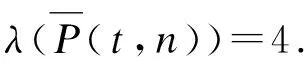
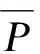
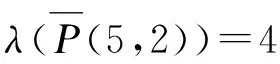
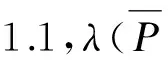
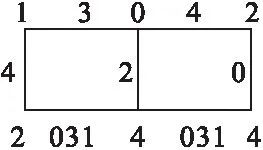
图5(a)

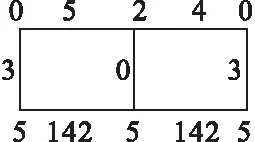
图5(b)

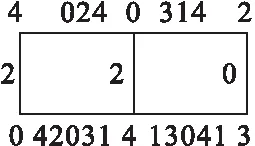
图6(a)

图6(b)

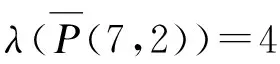
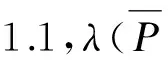
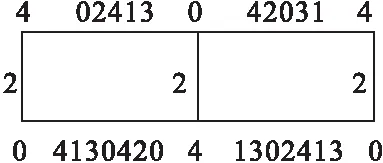
图7

图8

图9

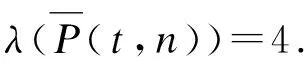
2 P(t,n)的(2,1)-全标号

由于拟梯子的(2,1)-全标号即其剖分图的L(2,1)-标号。则从第1节的结果，可得拟梯子的(2,1)-全标号数的结论。

定理2.1当t=2a=4或5≤t=2a+1≤7时，λT(P(t,2))=4,λT(P(t,n))=5(n≥3)；当t=2a≥6或t=2a+1≥9时，λT(P(t,n))=4。

[1] Griggs J R,Yeh R K.Labeling graphs with a condition at distance 2[J].SIAM J.Disc.Math,1992,5:586-595.

[2] Calamoneri T.The L(h,k)-labelling problem:a survey and annotated bibliography[J].Comput J,2006,49(5):585-608.

[3] Yeh R K.A survey on labeling graphs with a condition at distance two[J].Discrete Math，2006,306:1217-1231.

[4] Griggs J R,Jin X T.Recent progress in mathematics and engineering on optimal graph labellings with distance coditions[J].J Comb Optim，2007,14(2-3):249-257.

[5] Whittlesey M A,Georges J P，Mauro D W.On the lambda-number of Qnand related graphs[J].SIAM J.Discrete Math,1995,8:449-506.

[6] Havet F.(d,1)-total labeling of graphs[R].Workshop Graphs and Algorithms,Dijon(FRANCE),2003.

[7] Havet F,Yu M L.(d,1)-total labeling of graphs[R].Technical Report 4650,INRIA,2002.

[8] Wegner G.Graphs with given diameter and a coloring problem[R].Tech.Rep.University of Dortmund,Dortmund，1977.

[9] 杜娟,吕大梅,李冬冬,等.拟梯子的L(2,1)-标号[J].辽宁大学学报：自然科学版，2013,4:308-313.

[10] 丁海燕,吕大梅,王金华,等.拟Möbius梯子的L(2,1)-标号[J].辽宁大学学报：自然科学版，2014,4:293-299.

[11] 严冬梅,吕大梅.拟梯子的L(1,1)-标号[J].辽宁大学学报：自然科学版，2015,4:296-300.

[12] 吴飞， 吕大梅.点接拟梯子的L(1,1)-标号[J].辽宁大学学报：自然科学版，2016,1:1-6.

(责任编辑郑绥乾)

The(2,1)-total-labelingsofthesimilarityladders

JIN Xin,DANG Xun-jiao,LV Da-mei*

(DepartmentofMathematics,NantongUniversity,Nantong226007，China)

An(2,1)-total-labeling of a graph is a functionffrom the vertex set and edge set to the set of all nonnegative integers such that the labels are different for two adjacent vertices,and for two adjacent edges,and the difference of the labels between a vertex and an edge which are incident is at least 2.In this paper,we study the(2,1)-total-labeling of the similarity ladders,and completely determine the(2,1)-total-labeling number of the similarity ladders.

L(2,1)-labeling;(2,1)-total-labeling;(2,1)-total-labeling number;similarity ladder

O 157.5

A

1000-5846(2017)04-0306-04

2017-08-10

国家自然科学基金(11371207);江苏省自然科学青年基金(BK20140424);南通大学校级基金(14ZY009);南通大学大学生创新训练计划项目(2017067)

金鑫(1988-)，男，研究生，教师，从事运筹学与控制论研究.

*

吕大梅(1976-)，女，副教授，从事运筹学与控制论.