浅谈数列易错问题的解决策略

陈奇宜

(福建省福州民族中学，福建 福州 350000)

浅谈数列易错问题的解决策略

陈奇宜

(福建省福州民族中学，福建 福州 350000)

高中数列知识是数学学习的重要内容，也是高考的重要考试内容，但是许多学生在学习中经常会出现一些问题而导致解题错误.本文对数列易错问题进行了归纳总结.

高中数学；数列；易错问题；解决策略

数列知识是高中数学学习的重要内容，也是高考的重要知识点，许多学生在学习过程中经常会出现一些问题，导致解题错误.笔者结合高中数学教学实践，对数列学习中经常出现的易错问题进行了总结，以期对数列教学有所帮助.

一、对概念理解不准而导致错误

例1 数列{an}是递增数列，并且对于任意的n∈N+，都有an=n2+λn恒成立，求实数λ的取值范围( ).

错因数列是以正整数N*(或它的有限子集)为定义域的函数，因此它的图象只是一些孤立的点.正确解题时需要加强对概念的理解.

二、对公式使用条件考虑不全导致错误

例2 数列{an}的前n项和是Sn=3n+2n+1，求通项an.

错解an=Sn-Sn-1=3n+2n+1-3n-1+2n-1+1=2×3n-1+2.

正解a1=S1=6.当n≥2时，an=Sn-Sn-1=3n+2n+1-3n-1+2n-1+1=2×3n-1+2.把n=1代入上式，a1=2不适合公式.

三、审题不细心忽略细节导致错误

例3 已知a1=-24的等差数列，从第10项起开始为正数，求公差d的取值范围.

错因上述解法 在审题时忽略了“开始”一词的含义，题目强调了第10项是该等差数列的第一个正项，应有a9≤0，所以解题时应加上这个限制条件，解题过程才完整.

四、忽略公式的基本特征而导致错误

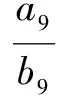
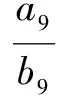
五、忽略题目隐含条件而导致错误

例5 有一个凸n边形，其各个内角的度数成等差数列，其中最小的度数是120°，公差为5°，求此凸n边形的边数.

错因由于凸n边形的每个内角的度数都小于180度，当n=16时，最大内角度数=120°+15×5°=195°>180°，不符合要求，应舍去n=16.

n2-25n+144=0，解方程得n=9或n=16.

当n=9时，最大内角度数=120°+8×5°=160°<180°;

当n=16时，最大内角度数=120°+15×5°=195°>180°，不符合要求舍去n=16.

∴凸n边形的边数是9.

六、忽略等比数列定义中的条件“公比q是常数”而导致错误

例6 已知一个数列{an}是首项为1的正项数列，并且(n+1)an+12-nan2+an+1an=0，n∈N*，求该数列的通项公式an.

总之，在数列题的求解中，应加强对概念和公式适用条件的理解和掌握，注意分析和总结常见易错的类型和原因，就能正确解答数列题目.

[1] 李芝举.高中数学解题方法浅谈[J].科技展望，2016 (07).

[2] 刘羿汎.探讨高中数学数列试题的解题方法与技巧[J].科学大众(科学教育),2016(11).

[3] 金姝萌.高中数学数列的解题常规方法分析[J].科技风,2016(24).

[责任编辑：杨惠民]

2017-07-01

陈奇宜(1978.6-)，男，福建省福州人，本科， 中学一级教师，从事高中数学教学.

G632

A

1008-0333(2017)28-0009-02