基于小波分析的跨海大桥斜拉索风致损伤识别

，，， ，

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014;2.浙江大学 建筑工程学院， 浙江 杭州 310012)

基于小波分析的跨海大桥斜拉索风致损伤识别

郭健1，徐洪东1，江定宇2，赵钦1，孙炳楠2

(1.浙江工业大学 建筑工程学院，浙江 杭州 310014;2.浙江大学 建筑工程学院， 浙江 杭州 310012)

海域环境下服役的斜拉索要承受强台风、环境腐蚀、重车过桥和温度效应等破坏荷载的作用，可能出现损伤破坏，降低拉索的强度和服役寿命.因此，如何有效快速地识别斜拉索是否发生了损伤，进一步识别出哪根索出现了损伤，这对于桥梁运营养护获得第一手的构件损伤信息是十分重要的.以浙江舟山跨海大桥中的金塘大桥为工程背景，建立了风荷载作用下的斜拉桥数值模型，基于小波分析方法研究了斜拉索损伤对桥面加速度测试信号的敏感性，实现了斜拉索损伤时刻的识别；构建了一种多尺度的损伤指标和损伤位置识别方法，进行了斜拉索损伤位置的识别，并分析验证了这种损伤识别方法的有效性和适用性.

跨海大桥；斜拉索；小波分析；风致损伤识别；损伤指标

跨海桥梁中经常采用大跨度斜拉桥的结构形式[1].如东海大桥、杭州湾跨海大桥和舟山连岛工程金塘大桥的主通航孔都采用了斜拉桥.从结构易损性分析的角度出发，海域环境下服役的斜拉桥要承受强台风、环境腐蚀、重车过桥和温度效应等破坏荷载的作用，斜拉索在复杂海域环境下将是易损构件，受到的损伤可能为索内钢丝疲劳断丝、索锚处损伤[2-4].这些损伤将降低结构的刚度和强度，从而引起更大的结构损伤积累，损伤积累到一定程度将可能导致结构的突发性失效[5]，如广州海印大桥的断索就造成桥梁进行换索.因此，斜拉索的损伤识别在跨海斜拉桥的运营中尤为重要，目前斜拉索损伤识别的研究方法，主要有：1) 基于动力指纹的分析方法.如Thabit等[6]以索振频率对损伤的敏感性来识别斜拉索损伤，但这种基于动力指纹分析方法的定位能力尚有不足之处；2) 基于人工智能的分析方法.如Arangio等[7]通过贝叶斯神经网络对斜拉索进行损伤识别，但这种基于人工智能的方法存在收敛性等问题；3) 基于统计的分析方法.如Sohn等[8]用一个统计过程技术来实现基于振动的索的损伤识别.但这种方法的理论模型需要较多实测的先验知识和先验验证；4) 基于系统识别的方法.这种方法主要是使用模型修正的方法，如Zhong等[9]以模型修正法对某座斜拉桥进行了损伤识别，但这种方法需要建立精确的有限元模型，且由于振动测试自由度不足以及测量信噪比高等原因，在应用上受到一些限制.

采用基于小波分析的方法来识别斜拉索的损伤.小波分析是近年来快速发展起来的一种时频域分析方法，能对稳态和非稳态信号进行多尺度分析.因小波具有多尺度分析的时频局部性等特征[10-11]，被广泛地应用于众多学科，在进行稳态和非稳态信号的特征提取、奇异性检测方面具有独特优势.研究中以浙江舟山跨海大桥的金塘大桥主通斜拉桥为工程背景，通过测试斜拉索与主梁连接处的加速度信号，基于小波分析研究加速度信号对斜拉索损伤的敏感性，构建斜拉索的损伤识别方法.

1 小波分析理论

小波分析是建立在传统的傅里叶变换的基础上发展起来的一种时频局部化分析方法，它的数学工具就是小波变换.传统的傅立叶变换，它的频域分辨率最高，但在时域无分辨率能力，只适用于分析平稳信号.而小波变换在时域和频域上同时具有良好的局部化性质，提供了一个灵活的时频窗，低频处时窗变宽，高频处时窗变窄，非常适合对含有稳态和非稳态成份的信号进行时频分析[12].因此小波分析非常适合对稳态和非稳态信号进行多尺度分析.

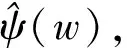
(1)

称ψ(t)为一个基本小波或母小波.将基小波ψ(t)经平移和伸缩后得到一组函数，称其为小波函数，即

(2)

式中：a为伸缩因子；b为平移因子.

对于任意函数f(t)∈L2(R)的连续小波变换，即

(3)

其重构公式为

(4)

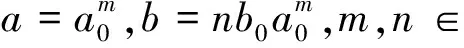
对ψ，a0，b0作某些特殊的选择，则ψm,n可以构成L2(R)的标准正交基.

2 面向损伤识别的数值模型

2.1 工程背景

浙江舟山跨海大桥中的金塘大桥是一座跨度为77 m+218 m+620 m+218 m+77 m=1 210 m的双索面五跨连续钢箱梁斜拉桥，采用半漂浮结构体系.如图1所示.主桥采用正交异性板板流线形扁平钢箱梁，梁高3.0 m，宽30.1 m.钢箱梁标准梁段为14 m，14 m梁段在横隔板处张拉斜拉索.斜拉索采用平行钢丝斜拉索，全桥共168根斜拉索.索塔为钻石形，采用C50海工耐久性混凝土.上塔柱高68.5 m，中塔柱高92.0 m，下塔柱高41.0 m.塔柱采用空心箱形断面.左塔在边跨和中跨各有21根索，分别为LB1～LB21，LZ1～LZ21；同样，右塔在边跨和中跨各有21根索，分别为RB1～RB21，RZ1～RZ21.

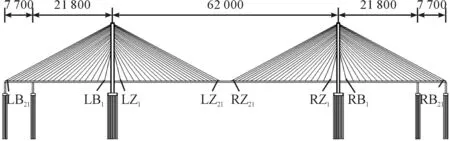
图1 大桥布置图Fig.1 Bridge layout

2.2 模型建立

为了选取合适的计算模型开展损伤识别研究，采用有限元分析软件ANSYS建立三种空间数值模型进行计算效率和计算精度的对比，分别为单主梁模型、三主梁模型和梁板组合模型.通过对比分析，单主梁模型与三主梁模型的静力计算结果差别很小，所显示出的结构动力特点更明显，而梁板组合模型的构造过于复杂，繁杂的建模细节易出现差错，并可能导致计算出现较大的误差.

基于数值建模的目标，并考虑静动力分析精度、计算效率因素，通过对比研究[13]，认为用于斜拉索损伤识别的大跨度斜拉桥有限元建模采用单主梁模型更适用，所建立的单主梁计算模型如图2所示.

图2 面向损伤识别的计算模型Fig.2 Numerical model of damage identification

在计算模型中，索塔采用三维变截面梁单元BEAM44来模拟，索塔横梁上的预应力以等效应力考虑，每个塔柱共划分161个单元；斜拉索采用三维杆单元LINK10模拟，弹性模量采用Ernst的等效弹性模量，斜拉索的初始应力换算成初始应变来施加，斜拉索通过一个横向刚臂和一个竖向刚臂与主梁相连；主梁采用等截面梁单元BEAM4模拟，共划分为365个单元，横隔板采用集中质量单元MASS21模拟，总共划分为366个单元；梁内压重块采用集中质量单元MASS21模拟，分配到对应的主梁节点上.索塔与钢箱梁之间设置了横向抗风支座和竖向支座，将桥面系下部与横梁在支撑位置处的节点在横向和竖向耦合；而在过渡墩和辅助墩的位置处，在中间梁对应位置处约束横向、竖向位移和绕纵向的转动.通过以上模拟，整个桥面系在纵向为半漂浮体系.

本桥位于I类地表，成桥状态下桥位处10 m高的100年一遇基本风速为40.16 m/s，颤振检验风速为81.8 m/s.100年一遇的主梁重心高度的基本风速介于47.59～48.34 m/s，在该风速下，大桥主要表现为抖振.因此在将风的作用转化为风荷载时，不考虑桥的自激力.数值计算中以AR(p)线性滤波器法生成主梁和桥塔上的风场.将作用在主梁上的风场离散为336个作用点的风速时程，将作用在桥塔上的风场离散为168个作用点的风速时程，各作用点按建立的有限元模型取计算节点位置.风荷载分为静力风荷载(平均风作用)和动力风荷载(脉动风作用).静力风荷载的施加是先计算结构相应节点上的平均风速，根据风洞实验得到的测力结果，计算桥塔上的阻力、斜拉索上的阻力以及主梁上的升力、阻力和扭矩，然后得到桥塔以及主梁上的静力风；动力风荷载的施加是将生成的风速时程代入Scanlan的准定常抖振力计算公式，求得抖振力后将抖振力施加于主梁节点上.施加风荷载后对结构做瞬态分析，采用Rayleigh阻尼，分析步长为0.2 s，计算时长为409.6 s.

2.3 数值分析与实测的频率特征对比分析

为了验证建立的有限元模型的有效性，将金塘大桥荷载试验实测的频率与有限元模型计算的前12阶频率进行比较，如图3所示.从图3中可以看出：通过有限元模型计算出的结构前12阶频率与实测频率相差不大，第1，2阶频率有微小偏差，第3，4，5阶频率基本重合，因此认为所建立的有限元模型还是十分接近实桥，能满足精度要求.同时，随着频率阶数的增大，计算模型的结构频率与实测频率间的误差有所增大，这主要是由于高阶振型与结构的局部振动特性相关，本计算模型对实桥局部细节的模拟还有误差.

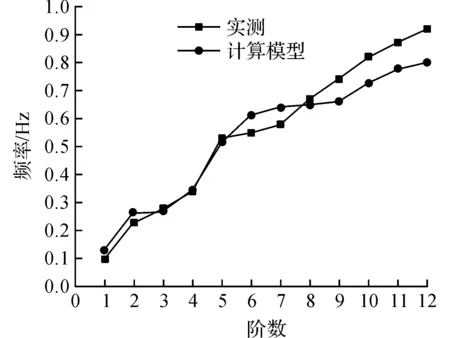
图3 计算模型频率与实测频率Fig.3 Comparison of frequency of calculation and test

3 敏感性分析及损伤指标构造

3.1 加速度信号的损伤敏感性分析

在桥梁结构监测中，桥面处的加速度信号一般比较容易获得，这里对计算模型中索梁节点处竖桥向(Z轴方向)的加速度进行数值采样，采样频率取200 Hz.计算中斜拉索的损伤模拟通过单元刚度的折减实现，假定损伤发生时刻为204.8 s，所取的损伤工况如表1所示.对加速度信号所做的小波分析的时程数据窗口在(204.8±60) s之间.

表1 索的损伤工况Table1 Damage condition of cable

在损伤工况1下，将计算模型中得到索梁连接节点处的所有加速度信号，用db6小波进行多尺度分析，以观察不同尺度的振动信息对索损伤的敏感性.取索损伤附近的节点350(LZ21与主梁的连接处)的加速度信号经小波分解和重构的结果如图4所示.

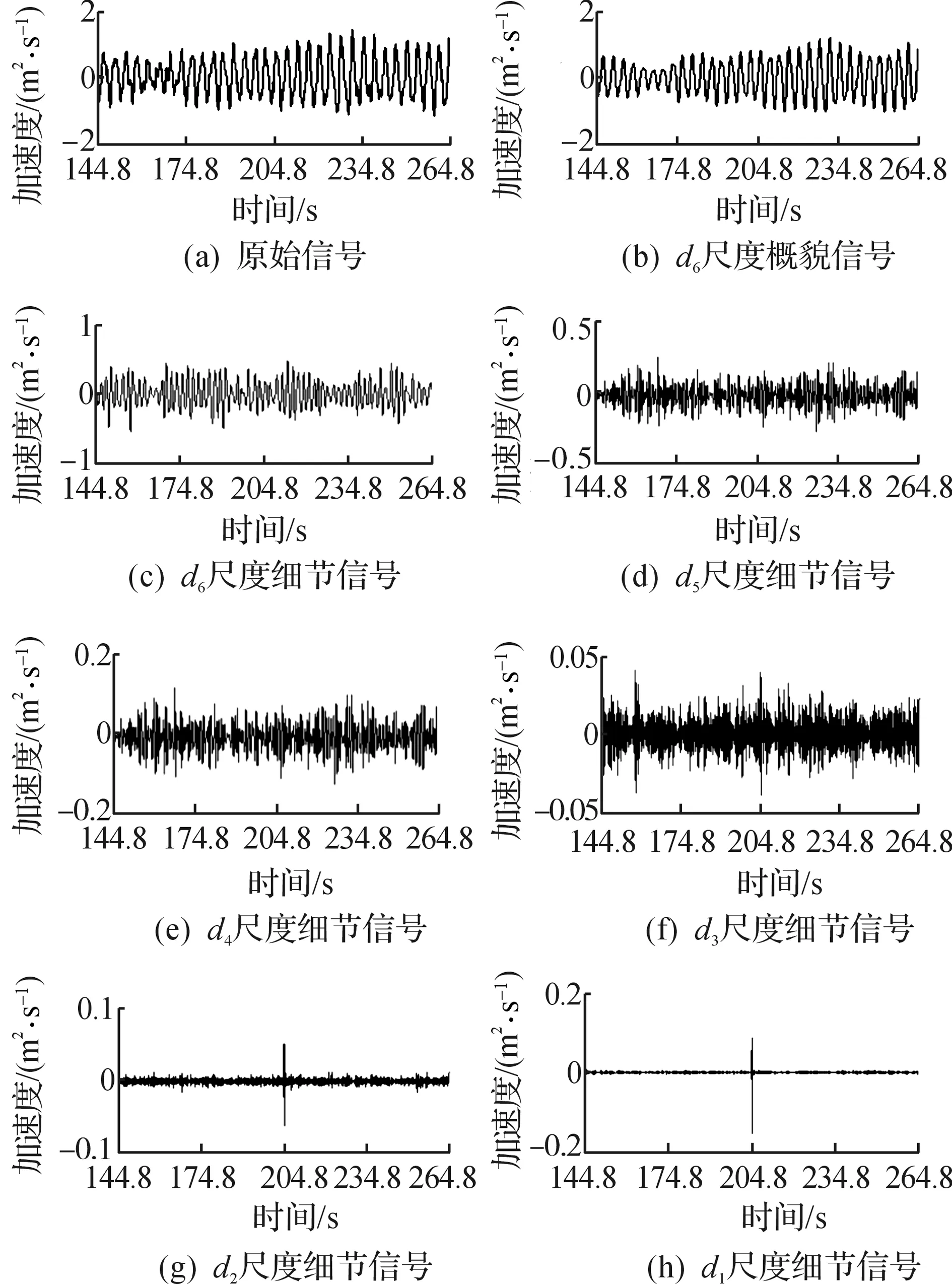
图4 节点350处加速度信号的小波分解Fig.4 Acceleration signal based on wavelet on 350

观察节点处的加速度信号在不同尺度上的小波分解信号，从图4可以看出：在加速度信号的不同尺度上所表现出的对损伤的敏感性不一样.图4中在d1尺度和d2尺度上都表现出了索出现损伤，发生损伤的时间点就是信号发生奇异性变化的时刻.

3.2 损伤指标构造

在线的健康监测系统中桥面加速度传感器一般可获取大量的连续观测数据，为了使小波变换的方法能用于快速分析连续监测数据，实现量化地反映损伤的发生.我们定义损伤指标为

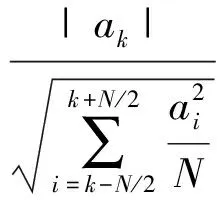
(5)

式中：ak为损伤发生的时间点τk上的信号；N为采集的信号数目，N=f0ΔT，ΔT为观察窗的宽度，取40 s；f0为采样频率，取50 Hz.

对图4中这样在索梁相接处的加速度小波分解信号用式(5)计算损伤指标λk时会发现，出现峰值的奇异点时刻和损伤出现的时刻并不完全重合，会出现微小的偏移，偏移量与小波基的选择有关.为了降低小波变换产生的偏移，更好地反映结构的损伤特性，选取损伤发生时刻附近范围内的最大值作为式(5)中的ak进行计算，即取max{ak-a,…,ak,…,ak+a}，a为需考虑的偏移量，这里取a=3.

4 斜拉索的损伤识别

4.1 损伤位置的识别方法

为了实现在大桥监测系统中索的自动损伤识别，需要在桥面各根索与梁的连接处布置加速度传感器，采集沿Z方向的加速度数据，在对每一个加速度数据进行小波多尺度分解后，再用式(5)分别计算每个加速度数据在d1和d2尺度上的损伤指标，以分析索的损伤信息.在数值计算中，拟定左塔与主梁跨中相连接的边索LZ21发生了损伤，以跨中为坐标原点，斜拉索LZ21与左塔、主梁的连接点在X方向(纵桥方向)上的坐标分别为-310 m和-8 m.LZ21发生不同程度的损伤时，Z方向的加速度信号在d1和d2尺度上的损伤指标沿主梁长度方向的分布规律如图5，6所示.

这里还需要设定损伤预警值的大小，把图5，6中的损伤指示程度分为比较清晰和非常清晰两级，通过大量索损伤的数值采样统计分析，可将预警指标设定为一级预警指标(d1=13，d2=12，如图中实线所示)和二级预警指标(d1=21，d2=19，如图中虚线所示).

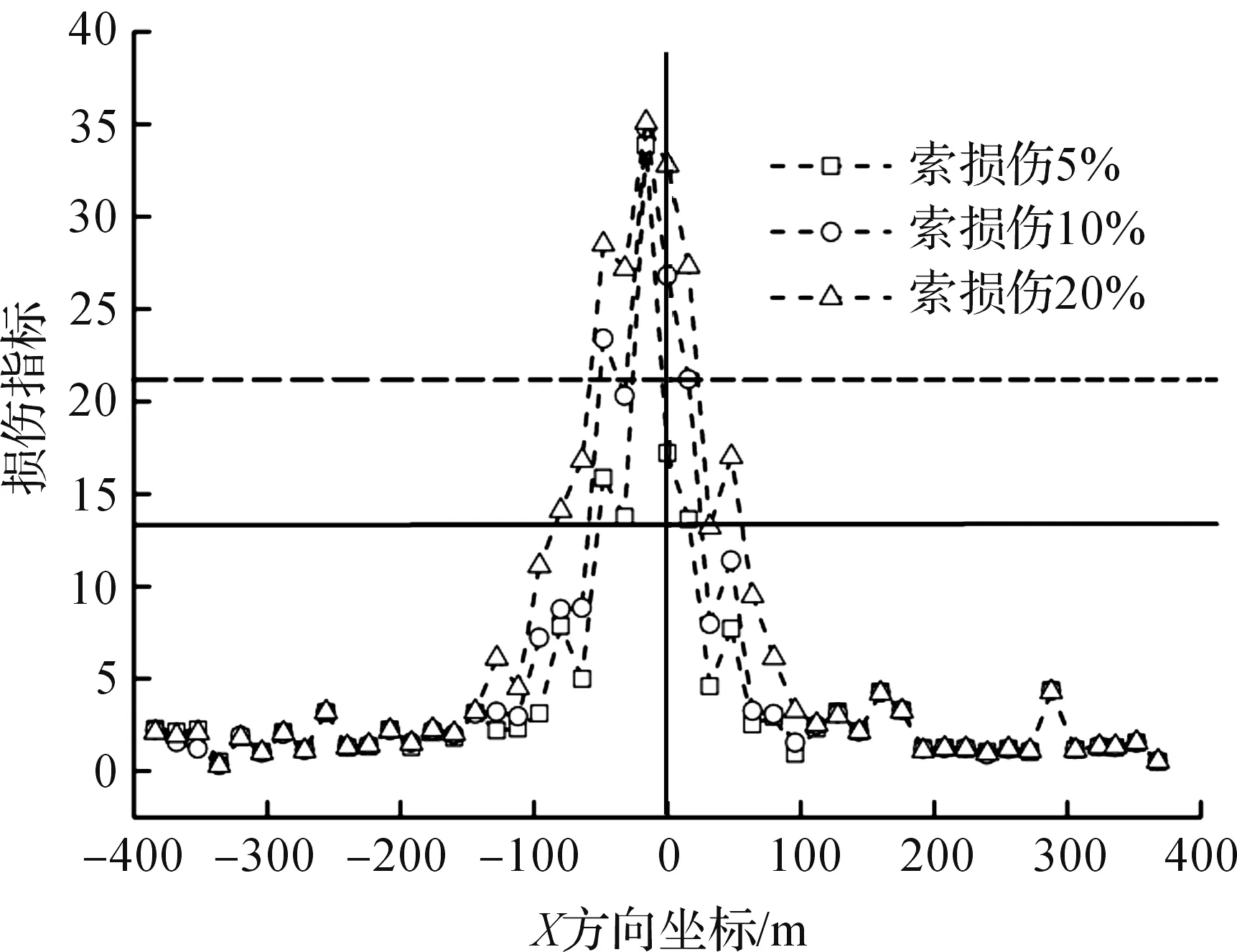
图5 d1尺度上的损伤指标Fig.5 Damage index on d1

图6 d2上尺度的损伤指标Fig.6 Damage index on d2

从图5，6中可以看出：随着损伤程度的增加，加速度信号在d1和d2尺度上的损伤指标在损伤索与主梁连接位置附近(约±100 m范围内)呈倒V形分布，峰值大，d1尺度增长较d2尺度更为显著，但d1尺度在损伤索与梁的连接位置处并无太大变化，这说明损伤索处的d1尺度上损伤指标对不同程度的索损伤是高度敏感的，并同程度的极大变化.同时也可以看出超越一、二级预警指标的个数与损伤程度是成正相关的.

考虑到加速度信号在d1尺度上的损伤指标在损伤索与主梁连接位置附近呈明显的倒V形分布，将损伤指标λk的峰值和与其相邻节点的值进行分析比较，如表2所示.从图6中可以看出：峰值和与其相邻节点的损伤指标能较明显地区别，由此认为Z方向d1尺度上的损伤指标可以作为损伤位置的判断依据.通过表2还可以看出：损伤指标峰值都较相邻左右节点的损伤指标值大，且损伤程度越小，损伤指标峰值与相邻节点的值相差越大.从而总结出对索损伤位置的识别标准，Z方向的加速度信号在d1尺度上损伤指标最大值处的斜拉索即为损伤索.

表2不同损伤工况下d1尺度上损伤指标λk的峰值及相邻节点上的值

Table2Damageindexλkofthepeakandadjacentjointond1scaleaboutdifferentdamagecondition

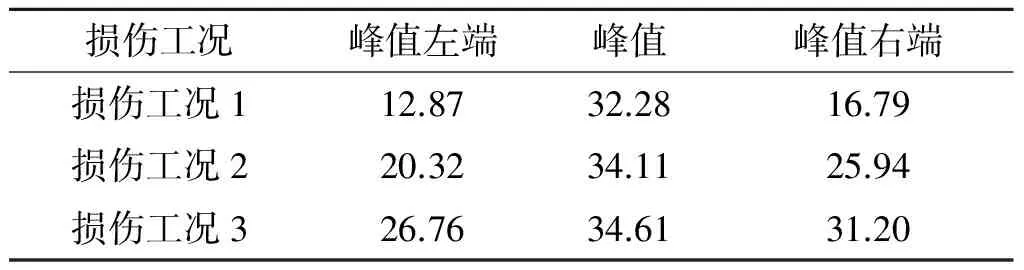
损伤工况峰值左端峰值峰值右端损伤工况112．8732．2816．79损伤工况220．3234．1125．94损伤工况326．7634．6131．20

4.2 损伤定位方法的适用性分析

上述分析是将位于大跨度斜拉桥跨中处的LZ21作为损伤索，这具有一定的特殊性.为了验证这种损伤定位方法对所有斜拉索的适用性，拟定了斜拉索LZ3和LZ11分别出现10%损伤时，应用构建的损伤指标λk来识别哪根索出现了损伤.d1尺度上的损伤指标值分别如图7，8所示.

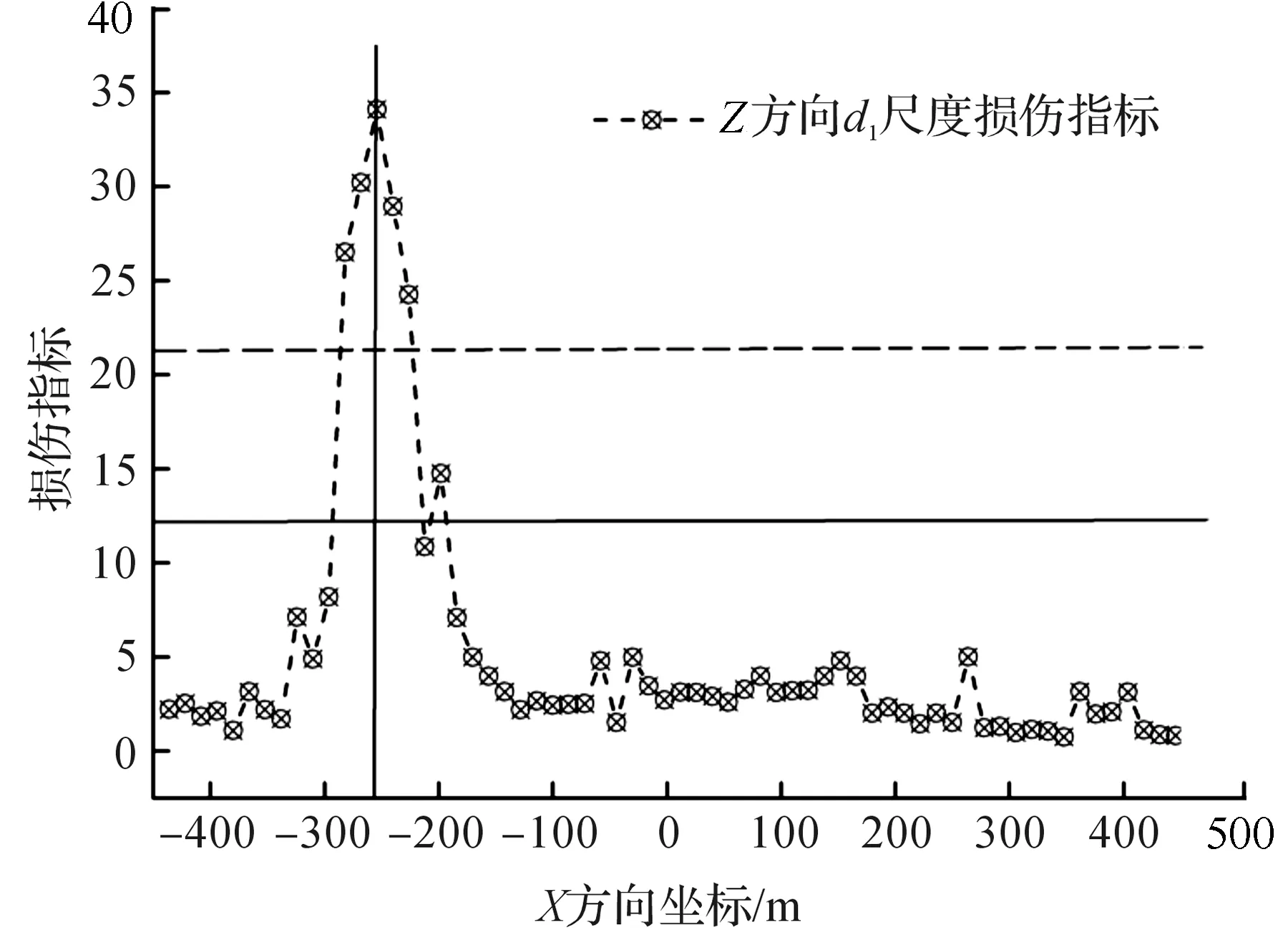
图7 斜拉索LZ3损伤10%Fig.7 10% damage of stayed cable LZ3

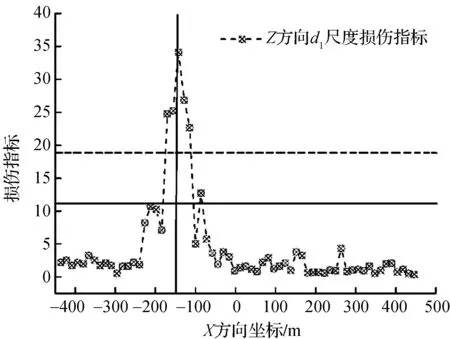
图8 斜拉索LZ11损伤10%Fig.8 10% damage of stayed cable LZ11

从图7，8可以看出：损伤指示明显，所建立的损伤识别指标和损伤定位方法适用性较好，均可识别出假定位置的斜拉索发生了损伤.但需要指出的是，对于桥塔和主梁边跨的支座附近位置处的斜拉索，上述损伤识别方法已不适用，这是因为在支座处，Z方向的主梁竖向位移和加速度都受到约束，失去了索的损伤信息.而支座处斜拉索的损伤风险也是最小的，可采用单独在这4根索上安装监测仪器来实现损伤识别.

4.3 损伤程度识别的方法思路

上述的损伤位置识别是通过分析Z方向d1尺度上损伤指标的峰值所对应的索梁节点位置来定位的.而从理论上讲，每根索的损伤程度与所有损伤指标λk中超越一、二级预警指标的个数及量值是正相关的，且具有一定的映射关系.因此，索的损伤程度识别就成为一个损伤模式识别的问题.按照模式识别的理论，通过统计更多的每一根索在不同损伤工况(更多损伤单元和损伤程度)下的损伤指标值及超越一、二级预警指标的数量，应用神经网络或其他非线性模式识别的算法，就可以实现索的损伤程度识别.这也是笔者下一步将要开展的工作.

5 结 论

斜拉索是斜拉桥的重要受力构件，其耐久性和安全性对于斜拉桥的正常使用和整体结构安全十分重要.笔者应用小波分析和数值分析，研究了风荷载作用下桥面加速度测试信号对斜拉索损伤的敏感性，并构建了一种基于小波多尺度分析的损伤指标和损伤定位方法，通过分析不同尺度上的损伤指标变化来识别大跨度斜拉桥拉索的损伤定位，并以多个索的损伤模拟，验证了方法的有效性和可行性.在得到初步损伤位置信息后，对于给定斜拉索的损伤程度判断即可结合不同的模式识别算法来进一步开展专项检测及识别.

[1] 张新军,虞周均,孙海凌.超大跨度斜拉桥空气静力稳定性研究[J].浙江工业大学学报,2014,42(2):182-189.

[2] SOHN H, FARRAR C R, HEMEZ F M. A review of structural health monitoring literature: 1996-2001[R].USA: Los Alamos National Laboratory Report,2003.

[3] 张清华.基于概率可靠度的结构损伤识别理论研究及应用[D].成都：西南交通大学，2006.

[4] 郭健,裘力奇,张新军,等.基于小波包分析的桥梁支座损伤识别试验研究[J].浙江工业大学学报,2016,44(6):695-698.

[5] 郭健,顾正维,孙炳楠，等.基于小波分析的桥梁健康监测方法[J].工程力学，2006,23(12)：123-134.

[6] THABIT A, FAHMY E, MOOTY M A. Damage identification using frequency sensitivity functions[R]. Canada: Canadian Society for Civil Engineering,2015.

[7] ARANGIO S. BONTEMPI F. Structural health monitoring of a cable-stayed bridge with Bayesian neural networks[J]. Structure and infrastructure engineering,2015,11(4):575-587.

[8] SOHN H, CZAMECKI J A, FARRAR C R. Structural health monitoring using statistical process control[J]. Journal of structural engineering,2000,126(1):1356-1363.

[9] 钟儒勉,宗周红,秦中远，等.基于多尺度模型修正的结合梁斜拉桥损伤识别方法[J].东南大学学报(自然科学版),2014,44(2):350-356.

[10] GUNSKI N, SHOKOUHI P . Wavelet transforms in surface wave analysis[J]. American society of civil engineers,2005,159(2):1-17.

[11] 兰秀菊,张丽霞,鲁建厦,等.基于小波分析和PSO-SVM的控制图混合模式识别[J].浙江工业大学学报,2012,40(5):532-536.

[12] 程正兴.小波分析算法与应用[M].西安：西安交通大学出版社,2001.

[13] 江定宇.大跨度桥梁的精细化损伤识别研究[D].杭州：浙江大学，2011.

Wind-induceddamageidentificationforstayedcablesofcross-seabridgesbasedonwaveletanalysis

GUO Jian1, XU Hongdong1, JIANG Dingyu2, ZHAO Qin1, SUN Bingnan2

(1.College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China;2.College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310012, China)

Stayed cables in sea environments have to bear strong typhoon, environmental corrosion, heavy vehicles, temperature effects, and other failure loads. As a result, damage may occur and the strength and service life of cables structures will reduce. Therefore, it is very important to effectively find the damage occurred in cables and to identify the damage cable for the operation and maintenance of bridges. A numerical model of cable-stayed bridges under wind loads is established based on the Jintang bridge in Zhoushan Zhejiang. Based on the wavelet analysis method, the sensitivity of cable-stayed damage to the acceleration test signal of bridge decks is studied and the damage moment is identified. A multi-scale damage index is proposed for identifying the damage locations of cables. The validity and applicability of the damage identification method are verified and analyzed.

cross-sea bridge; stayed cables; wavelet analysis; wind-indeced damage identification; damage index

2017-06-26

国家自然科学基金资助项目(50808160，51578506)；国家重点研发计划课题(2016YFC0802201)

郭 健(1973—)，男，甘肃兰州人，教授级高级工程师，博士，研究方向为桥梁工程，E-mail:Guoj@zjut.edu.cn.

TU4

A

1006-4303(2017)06-0671-06

(责任编辑：刘 岩)