基于吸引椭球体方法的鲁棒控制设计

苗润宁，张秀梅，崔 键

(山东科技大学 数学与系统科学学院，山东 青岛 266590)



基于吸引椭球体方法的鲁棒控制设计

苗润宁，张秀梅，崔 键

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

鲁棒控制理论已被广泛地应用在控制工程中, 而椭球体方法在解决控制系统的状态稳定性问题中具有传统算法所无法比拟的优势. 因此,针对一类离散时间非线性仿射系统提出了一种基于吸引椭球体的鲁棒控制设计方法. 在控制算法的设计过程中, 推广了传统的不变椭球体方法, 并给出一个等价的线性矩阵不等式(LMI)约束优化问题. 作为优化程序的结果, 得到了一个稳定的吸引椭球体, 该椭球体具有最小尺寸的特性. 最后, 通过数值仿真实例验证了所提出控制设计方法的有效性,这种分析方法为可实现的控制算法提供了理论基础.

鲁棒控制; 离散时间系统; 椭球体方法; LMI

基于李雅普诺夫的优化方法不仅为解决传统的稳定性问题提供了一种有用的理论工具, 而且在系统的鲁棒控制设计过程中有着广泛的应用[1-2]. 对带有有界扰动项的输入输出系统, 它的各种反馈控制问题在现代控制工程中已被公认为是具有挑战性的任务[3]. 最近, 各种动力学模型的鲁棒控制问题引起了众多研究者的关注. 因此, 相应的理论成果和应用程序得到广泛开发[4-5]. 作为非线性仿射模型的附加不确定性, 在稳定控制的设计过程中利用李雅普诺夫类型的方法是很直观的. 为了产生几乎稳定的轨迹, 主要工具之一就是椭球体方法[6]. 下面所要讨论的控制设计策略就是经典不变椭球体方法的一个推广.

在一些与闭环系统结构相关的假设下, 可以刻画一个吸引集合. 在现代控制工程中, 一般选择系统状态空间里具有椭球体形式的集合[7]. 在解决线性时不变系统的静态状态反馈控制器的综合问题时, 通过最小化相应的不变椭球体的尺寸, 最终简化为带有线性矩阵不等式(LMI)约束的优化问题. 选择必要的控制器参数，也就是增益矩阵, 可以最大限度地减小椭球体的尺寸. 本文利用李普希兹性质和李雅普诺夫函数等方法, 研究一类非线性离散时间仿射控制系统的鲁棒控制设计问题. 利用优化方法和Schur补引理等方法对系统的稳定性进行研究.

为便于阅读, 符号说明如下: MT表示任意向量或矩阵的转置; tr(M)表示方阵M的迹; M>0表示一个正定的对称矩阵; M≤0表示一个半负定的对称矩阵; Rk表示在2范数‖·‖意义下的k维欧式空间; R+表示正实数域; I表示单位矩阵; M⊗N表示集合M和N的克罗内克积.

1 系统描述与问题构建

考虑下面的非线性离散时间仿射控制系统:

(1)

假设1 系统(1)的右端项具有所谓的准李普希茨性质[8]:

(2)

假设2 (A,B)是可控的, (A,C)是可观的(可控性和可观性与系统(1)的线性化有关[9]).

假设3 矩阵BTB是可逆的.

现在, 系统(1)可重写为下面的等价形式:

(3)

系统(1)通常与一组可行的控制方程u(·)相关, 它的结构由下面的条件确定:

u(t)=Crxr(t)+Dry(t)

式中xr(t)∈Rn是一个“控制器状态”,Cr∈Rm×n和Dr∈Rm×k是增益矩阵. 控制器状态xr(t)满足

(4)

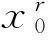
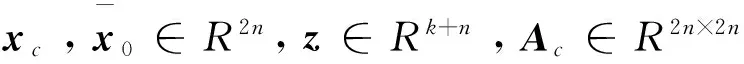
(5)

(6)

2 系统的鲁棒控制设计

2.1 吸引椭球体方法

为了扩展椭球体方法(吸引椭球体), 首先给出下面的引理.

引理1 如果函数γ: R+→R+满足下面的不等式:

Δγ(t)≤-αγ(t)+β

(7)

式中Δγ(t)=γ(t+1)-γ(t), 0<α<1 , β≥0, 则当t→时, γ(t)≤β/α.

证明 由已给条件可知

r(t+1)≤γ(t)-αγ(t)+β

则

r(t+1)≤(1-α)γ(t)+β≤(1-α)2γ(t-1)+(1-α)β+β≤

(1-α)3γ(t-2)+(1-α)2β+(1-α)β+β≤

⋮

(1-α)t+1γ(0)+(1-α)tβ+…+(1-α)2β+(1-α)β+β

即

引理2[9]对任意矩阵X,Y∈Rn×m和对称正定矩阵Λ∈Rn×n, 满足下列不等式:

XTY+YTX≤XTΛX+YTΛ-1Y

以及

(X+Y)T(X+Y)≤XT(I+Λ)X+YT(I+Λ-1)Y

在一维情况下, 引理2显然成立. 在主要定理证明过程中, 使用上述两个引理. 现在考虑以下的李雅普诺夫函数:V:Rn→R+,V(xc(t))=xc(t)TPxc(t).这个函数是在闭环系统(5)的轨迹xc(·)上考虑的, 令引理1中的常数α,β满足0<α<1,β>0, 则可得到(6)的一个等价表示:

(8)

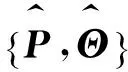
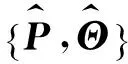
(9)

计算得出.

证明 即证明复合函数γ(t)=V(xc(t))满足不等式(7).

由引理2可知, 式中右端项包含下面的不等式:

所以

z(t,x)TΛ-1z(t,x)+αxc(t)TPxc(t)-αxc(t)TPxc(t)

所以

综上所述, 可得到

ΔV(xc(t))≤xc(t)TWxc(t)-αV(xc(t))+β

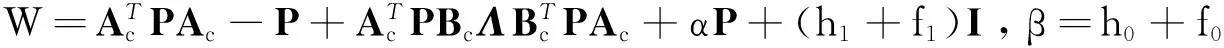
通过引理1, 得到当t→时,.由此可推断出, 当t→时,最终可得到(t)≤1+δ对所有的δ>0以及t>T(δ)成立, 其中T(δ)>0是一个足够大的数. 最后的不等式对R2n中的每一个初始点都是正确的. 所以, 由确定的吸引椭球体具有相应的最小化性质. 证毕.

定理1为本文的鲁棒控制方法提供了一个重要的理论依据. 与文献[10]中的不变椭球体方法相比, 提出的方法涉及一个特定的最小化问题, 并保证稳定不变集的一些最小尺寸性质.

2.2 优化问题的LMI表示

定理2 在定理1的假设下, 问题(9)中的双线性矩阵不等式约束可转化为下面的LMI约束:

(10)

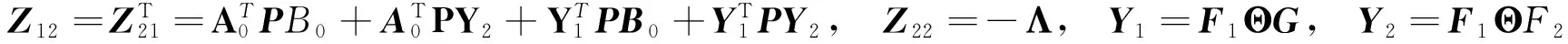
设优化问题为

(11)

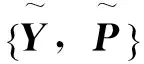
(12)

(13)

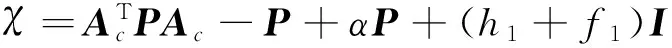
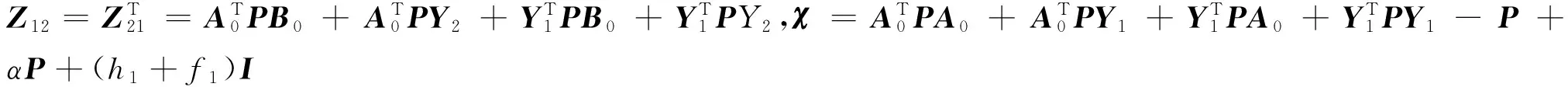
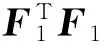
定理3 优化问题(11)的解也是优化问题(9)的一个最优解.

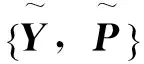
在本文中, 遵循鲁棒或实际稳定性的方法[11], 计算P使得相应的吸引椭球体ε的尺寸是最小的.

3 数值例子与仿真

考虑下面的非线性系统:

(14)

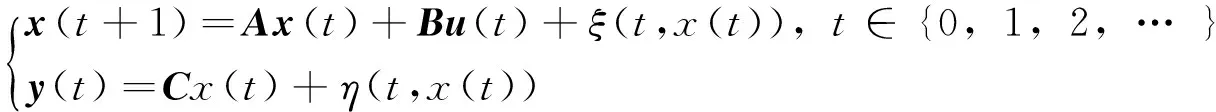
式中：ξ(t,x(t))=-Asign(x)+CT0.1sin(100t)-Ax(t),η(t,x(t))=0.1cos(100t),

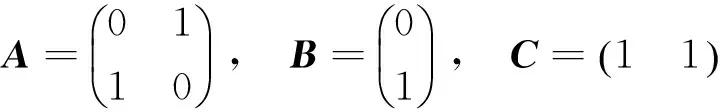
现研究两种情况: 一种是初始条件x0在ε内, 另一种是初始条件x0在ε外. 对第一种情形, 令x0=(-0.05, 0.01)T,在第二种情形中, 选择x0=(-4, 5)T,原仿射系统(2)的右端项通过下面的常数确定:f0=0.002,h0=0.038,f1=0.01,h1=0.01.

系统/控制器矩阵通过下面的矩阵确定:

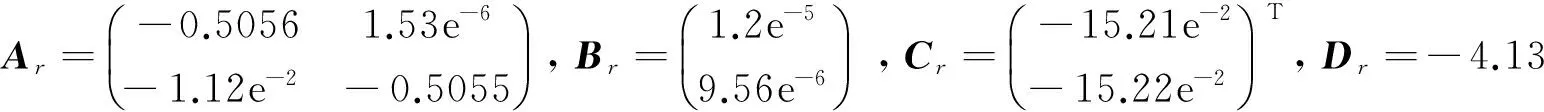
基于LMI-约束优化的标准MATLAB工具箱, 优化问题(11)的数值解为

这一实例证明了本文提出的鲁棒控制设计方法的数值有效性和潜在的实用性. 与一些可实现的鲁棒控制算法[7]相比,本文提出的方法是非线性规划中良好的计算方法，该方法在研究不确定系统的稳定性方面也存在明显的优势.

4 结束语

本文考虑了离散时间非线性系统的鲁棒控制设计问题, 针对一类非线性仿射控制系统, 基于吸引椭球体方法, 提出了一种新的鲁棒控制方法. 所得到的方法为设计闭环系统的稳定控制策略提供了理论依据, 该优化算法能够保证系统的稳定性(吸引区域的一些极小化属性), 数值算例验证了给定闭环系统鲁棒控制设计方法的有效性.

[1]SAKAIK,SHIBASAKIH,TANAKAR,etal.Adesignofarobustdiscrete-timecontroller[J].ISATransactions, 2015, 56: 155-164.

[2]KARAFYLLISI,JIANGZP.StabilityandStabilizationofNonlinearSystems[M].London:Springer, 2011.

[3]BASINM,RODRIGUEZ-GONZALEZJ,FRIDMANL.Optimalandrobustcontrolforlinearstatedelaysystems[J].JournalofTheFranklinInstitute, 2007, 344: 830-845.

[4]SONGMC,LINY.Arobustoutput-feedbackadaptivedynamicsurfacecontrolforlinearsystemswithinputdisturbance[J].ControlTheoryandTechnology, 2013, 11(2): 261-267.

[5]FRIDMANE,BLIGHOVSKYA.Robustsampled-datacontrolofaclassofsemilinearparabolicsystems[J].Automatica, 2012, 48(5): 826-836.

[6]AZHMYAKOVV.Onthegeometricaspectsoftheinvariantellipsoidmethod:Applicationtotherobustcontroldesign[C]//Proceedingsofthe50thConferenceonDecisionandControlandEuropeanControlConference.Orlando: 2011: 1 353-1 358.

[7]XUF,PUINGV,OCAMPO-MartinezC,etal.Set-theoreticmethodsinrobustdetectionandisolationofsensorfaults[J].InternationalJournalofSystemsScience, 2015, 46(3): 2 317-2 334.

[8]BLANCHINIF.SetTheoreticMethodsinControl(Systems&Control:Foundations&Applications)[M].Boston:Birkhauser, 2007.

[9]POZNYAKA.AdvancedMathematicalToolsforAutomaticControlEngineers:DeterministicTechniques[M].Amsterdam:Elsevier, 2008.[10]LOZADA-CASTILLON,POZNYAKA,CHAIREZI.Controlofmultiplicativenoisestochasticgeneregulationsystemsbytheattractiveellipsoidtechnique[J].InternationalJournalofControlAutomationandSystems, 2014, 12(5): 1 018-1 029.

[11]AZHMYAKOVV.Optimalcontrolofimpulsivehybridsystems[J].NonlinearAnalysis, 2008, 2(4): 1 089-1 097.

(编辑：郝秀清)

Robust control design via the attractive ellipsoid technique

MIAO Run-ning, ZHANG Xiu-mei, CUI Jian

(College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, China)

The robust control theory has been widely used in control engineering. And the ellipsoid method has the advantages which the traditional algorithms cannot match on solving the stability of dynamic systems. Therefore, this paper has concerned the robust control design through the ellipsoid approach. A new robust control design approach was proposed for a class of discrete-time nonlinear affine control systems. The design procedure was based on an extention of the conventional invariant ellipsoid method and a linear matrix inequality (LMI) constrained optimization problem was developed for the practical stability of the control systems. As a result of the optimization procedure, we obtained a stable attractive ellipsoid with some minimal properties (a minimal size ellipsoid). Finally, the effectiveness of the robust control design was illustrated by a numerical simulation,and this analytic method can provide a conceptual basis for the corresponding implementable control algorithms.

robust control design; discrete-time systems; ellipsoid method; LMI

2015-12-23

苗润宁，女， miaorunning@163.com

1672-6197(2017)01-0022-06

O231.2

A