材料力学中应力与应变的名称与正负定义

2017-11-22李依伦北京航空航天大学中法工程师学院北京100191北京航空航天大学航空科学与工程学院北京100191

力学与实践 2017年5期

李依伦李敏 ,1)(北京航空航天大学中法工程师学院,北京100191)(北京航空航天大学航空科学与工程学院,北京100191)

材料力学中应力与应变的名称与正负定义

李依伦∗李敏†,1)∗(北京航空航天大学中法工程师学院,北京100191)†(北京航空航天大学航空科学与工程学院,北京100191)

本文回顾了材料力学教材不同章节中应力与应变的名称，结合国标GB 3102.3-1993说明其与标准名称的关系；对比弹性力学的符号体系，给出材料力学符号体系的不同点以及转换方式.对于该问题的理解有助于讲授课程时规范名词定义，避免教材编写或讲授时符号定义的混乱.

应力，应变，材料力学

材料力学主要研究构件在外力作用下的受力、变形、破坏或失效的规律，主体内容围绕着内力、变形、应力与应变进行分析.由于材料力学课程的基础性与广泛性，国内存在众多版本的材料力学教材，其中在基本概念的名称与符号(本文中指正负号，下同)方面存在差异，部分教师对该问题不甚了解，容易在授课或答疑时造成误解.本文依据定义的对象与物理背景，讨论了应力和应变的名称与符号系统.

1 材料力学中应力与应变的名称

各位教师对于应力与应变的数学定义并无歧义，只是名称上 “各自为政”，例如有剪应力与切应力，线应变与正应变，剪应变、切应变与角应变等[15]，造成这种现象的原因一方面是教材编写中内容顺序与规范问题，另一方面与编写者的力学背景密切相关.

尽管材料力学教材的基本内容完全来自于西方，但在基本变形模式(与相应内力)的中文称谓方面并无乱象：轴向拉压 (轴力)、扭转 (扭矩)、弯曲(弯矩)、剪切 (剪力)均出自于对物理现象的描述，这些名称直观形象被广泛接受 (旧版教材中均提及4种基本变形模式，目前的新版教材中多将剪切归于连接件强度分析，剪力与弯矩均包含在弯曲模式中，所以只有3种基本变形模式).但应力与应变的定义涉及模型与方法，在同一外文单词的翻译上出现差异.

物体内部任意剖面上M 点应力的定义为

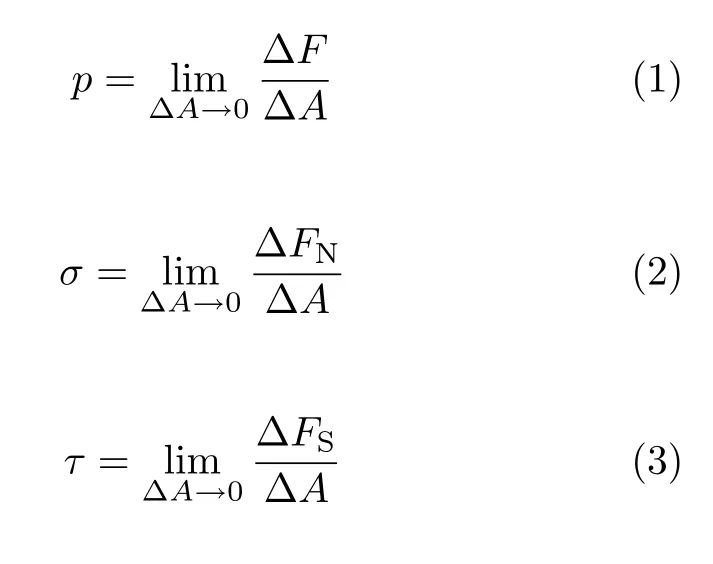
式中涉及内力∆F与作用面∆S如图1所示，由力的分解方向区分为作用面的法向分量∆FN与切向分量∆FS，由法向分量定义的内力集度σ称为正应力并无混乱，但切向分量对应的内力集度τ有剪应力与切应力两种名称.早期教材中均称为剪应力，其主要原因在于shear stress与shear deformation采用了同一单词.事实上，在扭转、弯曲基本变形模式中也存在该应力，应力的定义并不依赖于特定变形模式，所以采用变形模式的名称定义应力名称不甚合适.而切应力的名称体现了对应内力分量(或者应力分量)的方向，相对而言比较贴切.《中华人民共和国国家标准:力学的量和单位(GB 3102.3-1993)》规定的标准名称为切应力，这也是后期教材(包括改版教材)多采用切应力的原因.

相对于应力定义中出现的单一剖面模型，应变定义中有多种模型：一维、二维与三维(如图2∼图4)，不同的教材或者同一本教材的不同章节采用不同的模型，并给出不同的名称.

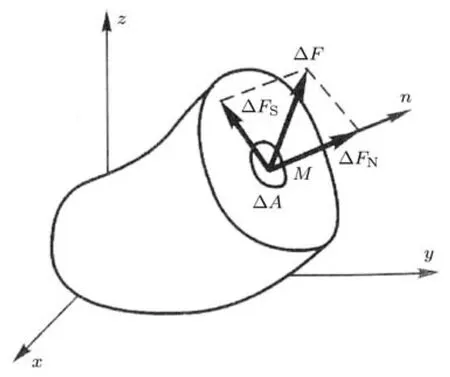
图1 应力定义示意图

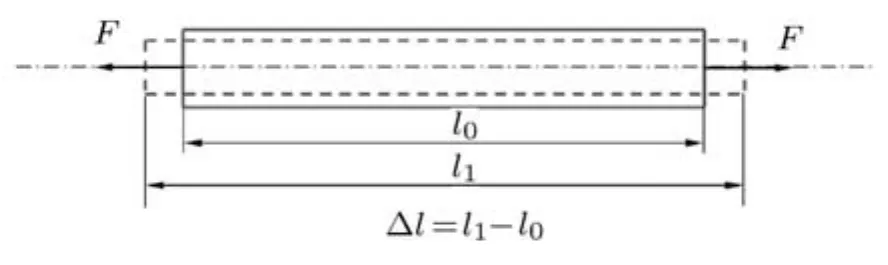
图2 应变定义一维模型示意图

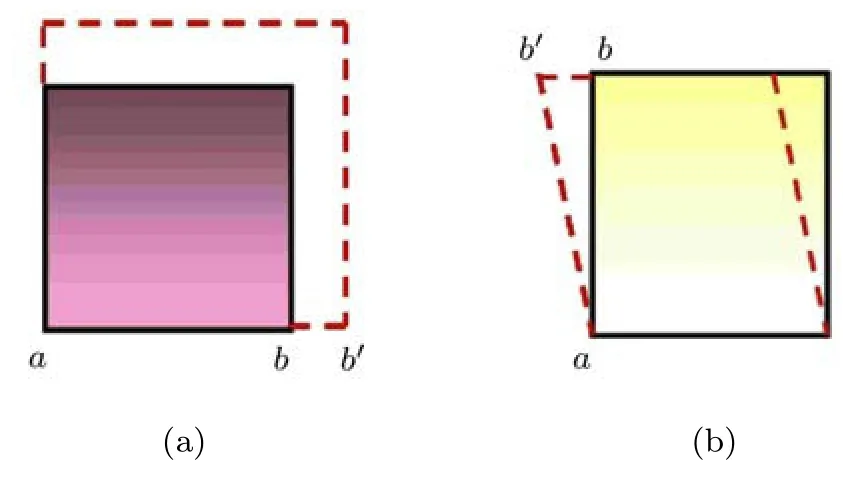
图3 应变定义二维模型示意图

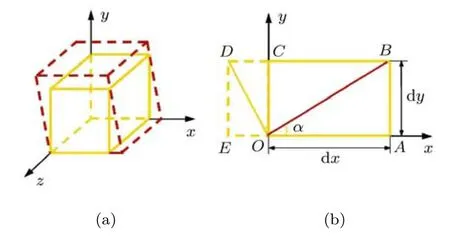
图4 应变定义三维模型示意图

长度的改变往往用一维(图2)或二维(图3(a))图像描述，其对象均为线段，由此定义的长度改变集度称为线应变形象合理 (在一维情况下还有称为拉应变与压应变的定义).同样的原因，如果使用二维模型 (图 3(b))描述形状改变，用夹角改变量表征，早期多称为角应变.如果对照应力的模式称为正应变与切应变，应该使用三维微元体(图4，其中图4(b)为平面应变状态下平行于xoy截面的简化分析模型)，因为在三维模型下才有面的法向位移与切向位移，由法向位移定义的应变称为正应变，由切向位移决定的应变称为切应变.

作为固体力学的基础课程，材料力学首次向学生展示变形体概念，物体的变形用尺寸的变化与形状的变化表征.针对三维微元体，其尺寸的变化常常用互垂三方向线段的变化表征，每个方向均为线段长度变化，而线应变是变化集度的表征；除尺寸的变化外，三维微元体形状变化使用原始互垂表面的歪斜衡量，这种变化就是互垂线段的夹角改变量.

在《中华人民共和国国家标准:力学的量和单位(GB 3102.3-1993)》中规定的应变名称为线应变(linear strain)与切应变(shear strain).线应变的定义式为 ε=∆l/l0，式中 l0是指定参考状态下的长度，∆l是长度增量；切应变的定义式为γ=∆x/d，式中∆x是厚度为d的薄层上表面对下表面的平行位移.

在名称上目前国内经典材料力学教材中有使用线应变的[12]，也有使用正应变的[3]，还有混合使用正应变与线应变的[4]；其他力学教材如经典弹性力学教材使用线应变[5]，工程力学教材使用正应变[6].国外教材使用正应变(normal strain)名称居多，包括其教科书与手册[58].切应变名称上没有差异.

从数学定义上几乎所有教材均不完全符合国家标准的定义方法，特别是切应变定义方法.事实上，国家标准中线应变与切应变的定义方法偏于宏观与近似计算而非概念表述.

鉴于目前国内外教材的现状，短期之内应变的名称与定义，特别是应变定义,完全统一至国家标准不现实.但从教学角度出发，教师了解名称与定义的出处与相互关系是有益的.

2 材料力学中应力与应变的符号

在大多数经典力学教材中采用弹性力学符号体系，为了说明材料力学符号体系的特点，先列出弹性力学的符号规定与对应图像.

2.1 弹性力学符号体系

弹性力学教材中规定应力正负的符号体系简单概括为 “正面正向与负面负向为正，反之为负”.此规定对于正应力与切应力均适用.

在弹性力学教材中较为常见的微元体应力状态如图5所示(图5(a)为可视面应力分布，图5(b)为隐藏面应力分布，由于单元无限小，因此没有增量项)，应力σij双下标中前者表示应力作用面，后者表示应力方向.作用面外法矢与坐标系正向一致为正面，否则为负面.由此规定可知,图5中无论正面与负面，其上标出应力的符号均为正.对于无限小的微元体，由此规定获得应力张量满足张量运算法则，与微元体力平衡一致，尤其是在描述切应力互等时，微元体中相关4个面的切应力不仅数量相等，符号也相同，即

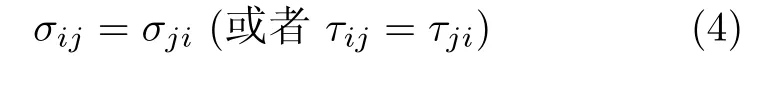
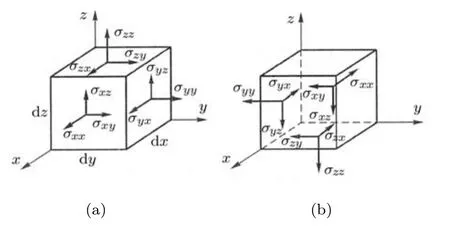
图5 应力符号规定与三维微体示意图

为了后续说明的简洁并与材料力学教材中应力应变状态分析相对应，图6给出了平面应力状态下的应力(图6(a)为微元体应力分布，图6(b)为平面示意图，图中为了与材料力学教材一致，使用τ表示切应力)，同样图中正面与负面的应力符号均为正.

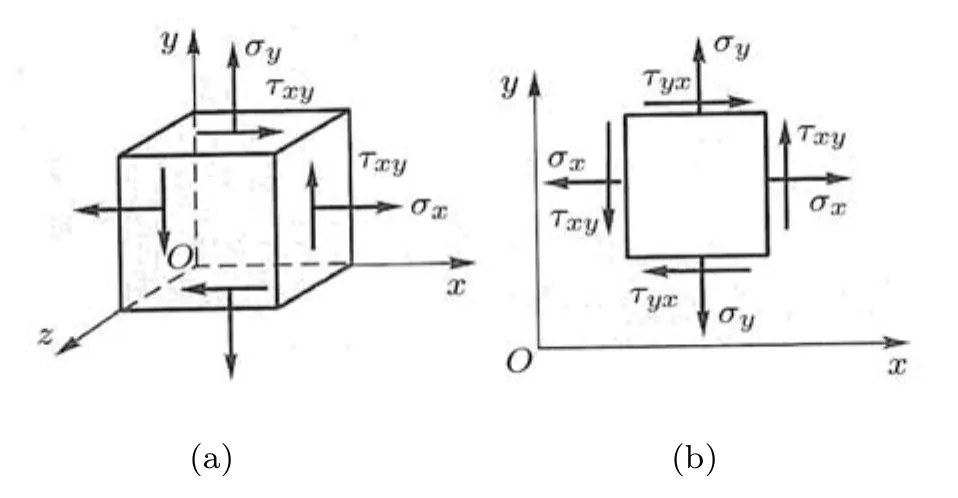
图6 平面应力状态下应力符号定义示意图

与图6完全对应的微元体变形与应变定义如图7所示(图7(a)为微元体变形，图7(b)为对应的切应变定义示意图)，正应变的符号跟随变形的符号：正面正向移动与负面负向移动为正，反之为负.这里单独给出切应变γxy的数学定义为

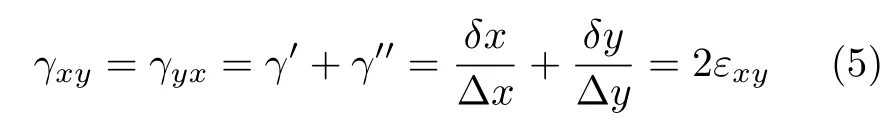
其中,γij就是材料力学中的切应变(在弹性力学中称为工程切应变)，而 εij是弹性力学中的应变，当i/=j时就是切应变.此图中γ′与 γ′′均为正，因为δx与 δy为正，尽管 γ′与 γ′′分别对应顺时针与逆时针转动.

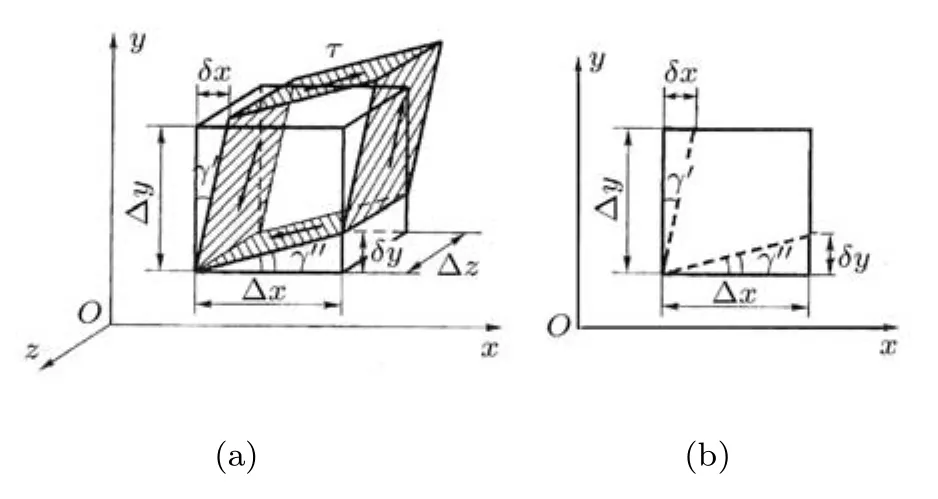
图7 平面应力状态下切应变与符号定义示意图

在Timoshenko经典教材中有如下的描述[9]：Shear strain in an element is positive when the angle between two positive faces(or two negative faces)is reduced.The strain is negative when the angle between two positive(or two negative)faces is increased.简言之，两正面或两负面夹角减少时切应变为正，否则为负.

2.2 材料力学符号体系

为了表达简洁并符合大部分材料力学教材的模式，此处仅给出微元体应力与应变的平面图形(图8为讲述广义Hooke定律中均出现的图形)，图8(a)为平面应力情况下的应力分布，图8(b)和图8(c)为对应的载荷分解与变形.

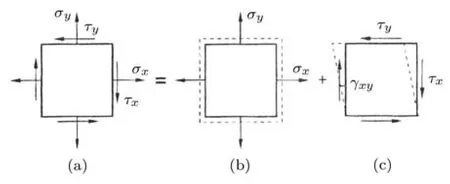
图8 平面应力状态下应力与变形示意图

在材料力学教材中应力的符号定义为：正应力拉正压负，切应力以使微元体顺时针转动为正，逆时针转动为负.图8中各面的正应力全为正，x面的切应力为正，y面的切应力为负.

与之对应的应变符号定义为：正应变伸长为正，缩短为负；切应变以直角变大为正，减小为负.图8中各面正应变为正，微元体切应变以左下角直角(或右上角直角)的变化表征，直角变大表示该点的切应变为正，也有教材描述为两正面(或两负面)直角变大为正.

事实上，在材料力学符号体系中其正负定义与坐标系并无直接关联.

对比图6∼图8可以发现，由弹性力学体系定义的应力与应变符号体系中，正应力与正应变的符号与材料力学符号完全相同，但是切应力与切应变符号不同：

•弹性力学体系中切应力符号遵循正面正向与负面负向为正，反之为负 (图 6中各面切应力均为正)；切应变以直角变小为正.

•材料力学体系中切应力以企图使微元体顺时针转动为正，逆时针转动为负(图8中x面的切应力为负)；切应变以直角变大为正.

因此引出的问题是：人们为什么在材料力学中采用此种特殊的符号规定？

2.3 符号差异的原因与转换

材料力学课程中提及符号体系始于截面法求内力，其不依赖于坐标系的符号规定意在协调两个分离体同一假想截面上的内力符号.仅就该作用而言，使用弹性力学正面正向负面负向符号规定可以获得同样的效果，至今仍然采用其特殊规定涉及另一内容--应力圆.

在材料力学发展史上，德国科学家同时也是优秀的工程师库尔曼(Culmann)与摩尔(Mohr)在图解法方面作出卓越贡献[6]：库尔曼在 1866年出版的《图解静力学》中证明,二维物体中一点的二向应力状态可用平面上的一个圆表示，这样可使问题的分析大为简化.摩尔对应力圆作了进一步的研究，1882年出版的《土木工程》给出了借助应力圆确定一点应力状态的几何方法，后人就称应力圆为摩尔应力圆，简称摩尔圆.图9是材料力学教材应力应变状态分析部分的应力圆常见图样.

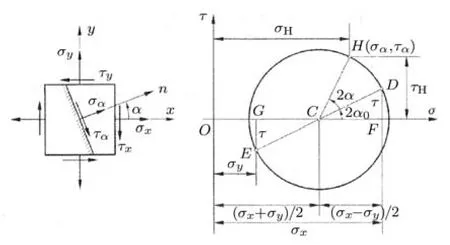
图9 平面应力状态下应力圆示意图

从图9可以看出一个简单的事实：无论x面与y面的应力如何分布，采用弹性力学的符号体系不可能获得应力圆--图9中D点(对应x面)与E点(对应y面)的切应力必须反号，而采用弹性力学符号规定，根据切应力互等，x面与y面的切应力或者全部为正，或者全部为负，符号不可能相反.

目前采用弹性力学符号体系的材料力学教材在讲述到该部分时，或者重新改回材料力学符号体系，或者采用符号转换规则.

如果采用符号转换,有两种方法：方法1：应力圆坐标系中横坐标(正应力σ)向右为正，纵坐标(切应力τ)向下为正；x面切应力保持正面正向、负面负向为正的模式，但y面切应力转为正面正向、负面负向为负；应力圆中方位角2α与单元体中方位角α同向，均以逆时针为正.方法2：应力圆坐标系中横坐标(正应力σ)向右为正，纵坐标(切应力τ)向上为正；x面切应力转为正面正向、负面负向为负，y面切应力保持正面正向、负面负向为正的模式；应力圆中方位角2α与单元体中方位角α反向，后者逆时针转动对应前者顺时针转动.

无论采用哪种方法，相互垂直两面中总有一面不能采用弹性力学符号体系.第一种方法尽管纵坐标向下为正，但应力圆中方位角与单元体中方位角同向，这种对应关系比较直观，所以相对而言采用第一种转换方法的教材较多.

除了应力圆的绘制与对应关系，如果采用弹性力学符号体系，在应力转轴公式(或应变转轴公式)的图像理解上与材料力学符号体系不同，下面以应力转轴公式为例说明.

采用材料力学符号体系，图 9所示应力分布下，α面(x轴正向逆时针转动α角)应力为

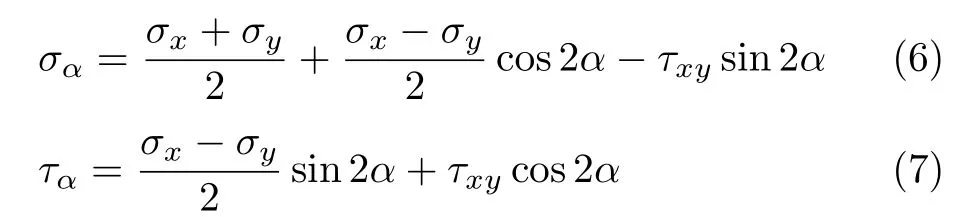
按照材料力学转轴公式的物理解释，式 (6)与式(7)表示平面应力状态下某一点应力不同方向的正应力与切应力分量.由此可以解释计算结果，例如 α =0◦,σ0° = σx,τ0° = τxy就是 x 面的应力情况；当 α =90◦,σ90°= σy,τ90°= −τxy就是 y 面的应力情况，其中切应力前的负号表示y面的切应力具有使微元体逆时针转动趋势.对照图9解析公式与图像完全符合.

采用弹性力学符号体系，图6所示应力分布下(注意x面与 y面的切应力全为正)，α面应力表达式为

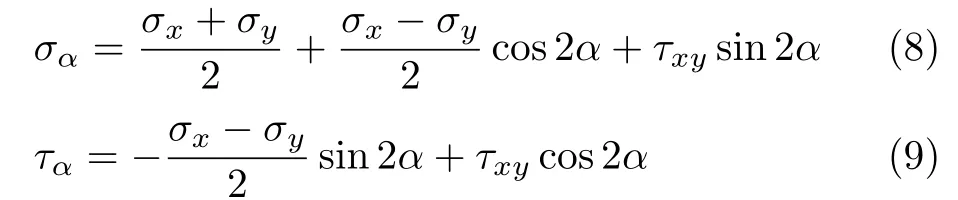
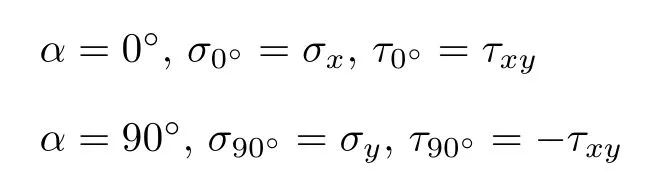
与之对应,根据式 (8)与式 (9)，同样考察两个方位0◦方位的结果与 x面一致，90◦方位的正应力与 y面一致，但切应力y面反号，该结果对照图6不易理解.

理解该问题应回归弹性力学符号体系的基础：弹性力学符号体系依赖坐标系的定义，此处应力转轴公式的物理含义解释为应力在不同坐标系下分量之间的转换关系.按照这种解释，0◦的结果表示新坐标系与旧坐标系一致时新的x面应力就是旧的x面的应力；90◦的结果表示新坐标系中 x面正应力与旧坐标系中y面正应力一致，新坐标系中x面切应力在数量上等于旧坐标系中y面切应力，但符号相反，因为新坐标系的x面正向与旧坐标系的y面正向相反.

平面应变状态下应变转轴公式有相同的问题，此处不再赘述.

3 小结

目前绝大部分院校对于材料力学课程的讲授依照归纳法的模式(从拉压、扭转与弯曲几种基本变形模式开始，然后归纳出应力应变状态与强度理论)，其优势是由简入繁、由浅入深，但由此也造成同一物理量名称的差异 -- 不同章节涉及同一物理量时对象不同或者简化模型不同，为了讲述的方便各自采用了“局部最优”的描述.相对而言，如果按照演绎法体系，应力应变名称均在三维微体模型上定义就能避免该问题，或者在课程后期总结时进行名称辨析对学生是有益的.

另一方面，除应力圆部分外，材料力学教材完全可以采用弹性力学符号体系，包括采用二阶张量矩阵的坐标转换法则给出应力转轴公式，以及采用三阶实对称矩阵特征值问题分析主应力 (特征值为主应力，特征向量为主方向)，对于从事力学理论工作的研究者，这种模式是简洁与优美的.但是材料力学的特色是分析方法与表现形式与工程应用密切相关，其中概念与结果的图像表征深入人心，应力圆部分也是重点内容.只要应力圆部分存在，材料力学教材就无法把弹性力学符号体系贯穿始终.至于如何选择是教师的偏好，但与前述问题类似，最终给学生一个解释以避免混乱还是有益的.

1 孙训方等编.材料力学(第5版).北京：高等教育出版社，2009

2 刘鸿文编.材料力学(第5版).北京：高等教育出版社，2011

3 单辉祖编.材料力学(第3版).北京：高等教育出版社，2010

4 范钦珊.材料力学(第3版).北京：高等教育出版社，2014

5 徐芝纶编.弹性力学(第4版).北京：高等教育出版社，2006

6 梅凤翔编.工程力学.北京：高等教育出版社，2005

7 Gere JM.Mechanics of Materials，第 5版.北京：机械工业出版社，2003

8 Young WC,Budynas RG.Roark’s Formulas for Strain and Stress.7th edn.New York:McGraw-Hill Companies Inc,2002

9 Timoshenko SP.History of Strength of Materials.New York:Dover Dublication,1983

O341

10.6052/1000-0879-17-068

2017-03-02收到第1稿，2017-04-12收到修改稿.