具有多种备选方案的露天矿统一运输调度优化①

田谦益

(闽南师范大学 计算机学院, 福建 漳州 363000)

具有多种备选方案的露天矿统一运输调度优化①

田谦益

(闽南师范大学 计算机学院, 福建 漳州 363000)

受客观条件限制，使得露天矿统一运输调度的优化存在多个复杂约束，需要多种备选方案的问题.提出了一种新型优化方法，该方法采用一种自适应的惩罚函数方法来处理约束，然后运用多元优化算法进行优化.该自适应惩罚函数参数少，简单高效，对问题依赖小.多元优化算法将搜索个体按其不同的功能组合成一个特殊的数据结构，利用该结构保存和共享寻优过程信息，实现搜索过程记忆，能以较大概率找到最优解，同时保留多个次优解.以某露天铁矿为工程应用实例研究，将该方法与GA、PSO-w、DMS-PSO-HS几种群智能算法的优化结果进行比较验证，结果表明本文提出的方法在露天矿统一运输调度优化中处理约束简单、高效，能够提供多种备选方案且最优解精度更高.对露天矿统一运输调度优化问题进行多个备选方案的研究具有理论依据和实际意义，采用该方法进行具有多个备选方案的露天矿统一运输调度优化是可行有效的.

露天矿，惩罚函数，多元优化算法，搜索元，过程记忆

露天矿通常存在多采掘点、多排卸点，从而形成物料流的多条通道.而露天矿的生产主要是大量物料的运移，运输成本一般占整个露天矿生产成本的50%以上，是影响矿山经济效益的重要因素[1].国内外露天矿运输设备与物料的匹配情况主要分为3种类型：统一运输、独立运输和组合运输，其中统一运输是指每台卡车可以运输任何物料、可以到任何装载点装车、到任意排卸点卸车, 实际上是把矿山车流规划问题简化为多个装载点和多个卸载点之间的车流规划问题, 这是目前应用成果的主要体现[2].

近年来已有不少学者将遗传算法、粒子群算法等群智能优化算法用于露天矿运输调度问题，取得了较好的结果[3-7].但这些方法都只能给出一个最优方案，而在实际露天矿独立运输调度中，野外环境较为恶劣，容易出现塌方使道路中断等类似事件，导致运输线路需要调整，原有的最优方案失效，从而增加运输成本.此时若能启用备选方案，就能适应外界环境变化，快速调整运输调度计划，减少因临时变化给生产带来的损失.因此，如何根据外界环境变化从多个备选方案中选择和确定矿石及岩石的合理调运方案，在满足多个复杂约束的条件下，使得运输成本在一定的运输网络中最小，是露天矿优化设计中需要解决的重要问题之一.为实现这一目的，本文采用一种新型方法来解决露天矿独立运输调度的优化问题.该方法采用一个参数少、效率高自适应惩罚函数来处理复杂约束，然后运用多元优化算法(multivariant optimization algorithm，MOA)进行优化.

1 露天矿运输调度模型

露天矿的生产主要是由电铲车装车、电动轮自卸卡车(以下简称卡车)运输来完成.卡车一旦调用,则在1 个台班内不熄火.以节约生产成本为目的,统一运输可归结为一个总运输成本最小的多变量带复杂约束的线性规划模型，模型见式(1)，表1给出了模型中的符号参数设定.

(1)

其中式(1)中，f(x) 为目标函数，表示一个台班内总运量的最小值；xij,xik为整数型决策变量，其中xij为从铲点i运往卸矿点j的运输车次，xik为从铲点i运往卸岩点k的运输车次.

2 多元优化算法在露天矿独立运输调度中的优化

表1露天矿运输调度系统模型参数设定

符号含义i(i=1，…，l)台班中的铲装点编号j(j=1，…，m)台班中设置的卸矿点的编号k(k=1，…，n)台班中设置的卸岩点的编号dij/dik为铲装点到卸矿/岩点的距离cij/cik单次铲点到卸矿/岩点的满载费用cji/cki单次卸点到卸矿/岩点的空载费用pi各铲点的岩石量qi各铲位的矿石量Mj台班卸矿点的产量要求Mk台班卸岩点的产量要求Qj各卸矿点的矿石品位要求T矿车满载量ai铲点矿石的平均品位am/ai为卸点要求品位上/下限t1装车时间t2卸车时间t3一个台班工作时间

2.1 多元优化算法

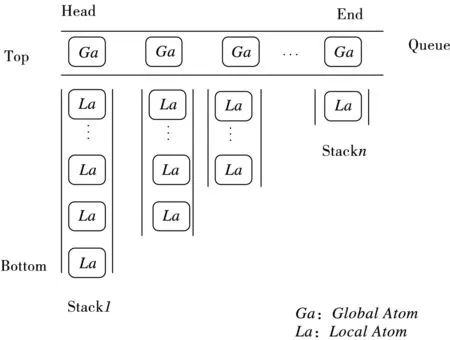
图1 MOA的数据结构

经典的群智能算法及其改进算法在解决不同问题时有着各自不同的优势，但都不同程度地存在着全局探索与局部开发相互制约，易陷入局部最优的问题.究其原因主要是一些复杂问题的全局最优解被大量的局部最优解所包围，具有较大欺骗性，而算法在寻优过程中信息利用不充分，导致算法陷入局部最优.只有算法合理地处理全局探索和局部开发之间的关系，同时充分利用寻优过程信息，才能找到全局最优解[9].多元优化算法采用一种新型的数据结构存储和充分利用寻优过程信息，MOA中的进行搜索的个体为搜索元，搜索元按照不同的功能分为两类，一类搜索元是全局搜索元(GlobalAtom，Ga)负责全局搜索，另一类搜索元是局部搜索元(LocalAtom，La)负责局部挖掘，全局搜索元以队列的形式排列，局部搜索元以堆栈的形式排列，构成一个特殊的数据结构体.该结构体如图1所示，顶部是由全局搜索元构成的队列，每个全局搜索元下挂一个局部搜索元构成的堆栈，每迭代一次，MOA对整个解空间进行全局搜索，找到具有开发潜力的区域；然后对各个有开发潜力的区域进行挖掘，找到该区域里的最优解，排在堆栈顶端，成为全局最优解，然后这些最优解再进行比较，将最优的全局最优解排在队列的最左端，这样每次迭代结束时，当前的全局最优解都出现在队列的最前端，下挂与其对应的多个局部最优解，保留了寻优过程信息.在整个迭代过程中，全局搜索和局部挖掘都同时存在，共享寻优信息，使算法不易出现过早收敛，提高算法寻优性能.

全局搜索元根据式(2)生成

(2)

式中d是问题的维度；maxi和mini分别为解空间第i维的上、下限；hi为一个介于mini到maxi之间均匀分布的随机数.局部搜索元根据式(3)生成

(3)

式中r为局部邻域半径,决定了局部邻域的范围；li,(i=1,…,d)为一个介于-1到1之间均匀分布的随机数.

2.2 多元优化算法优化露天矿独立运输调度模型

露天矿运输调度问题可以归结为一个带复杂约束的线性规划问题，复杂约束处理的好坏，直接影响到是否能找问题的全局最优解.在处理复杂约束的方法中，有基于罚函数的方法、基于搜索可行解的方法等[ 10-11].本文采用一种新型的罚函数的方法来处理复杂约束，先构造适应度函数如

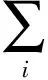
(4)

式中f(x)的是原问题的目标函数，φi(x)为第i个约束条件，且φi(x)≤0，K为惩罚函数.惩罚函数的好坏，决定了能否在迭代过程中正确权衡目标函数与约束条件之间的关系.因此，本文构造的惩罚函数如

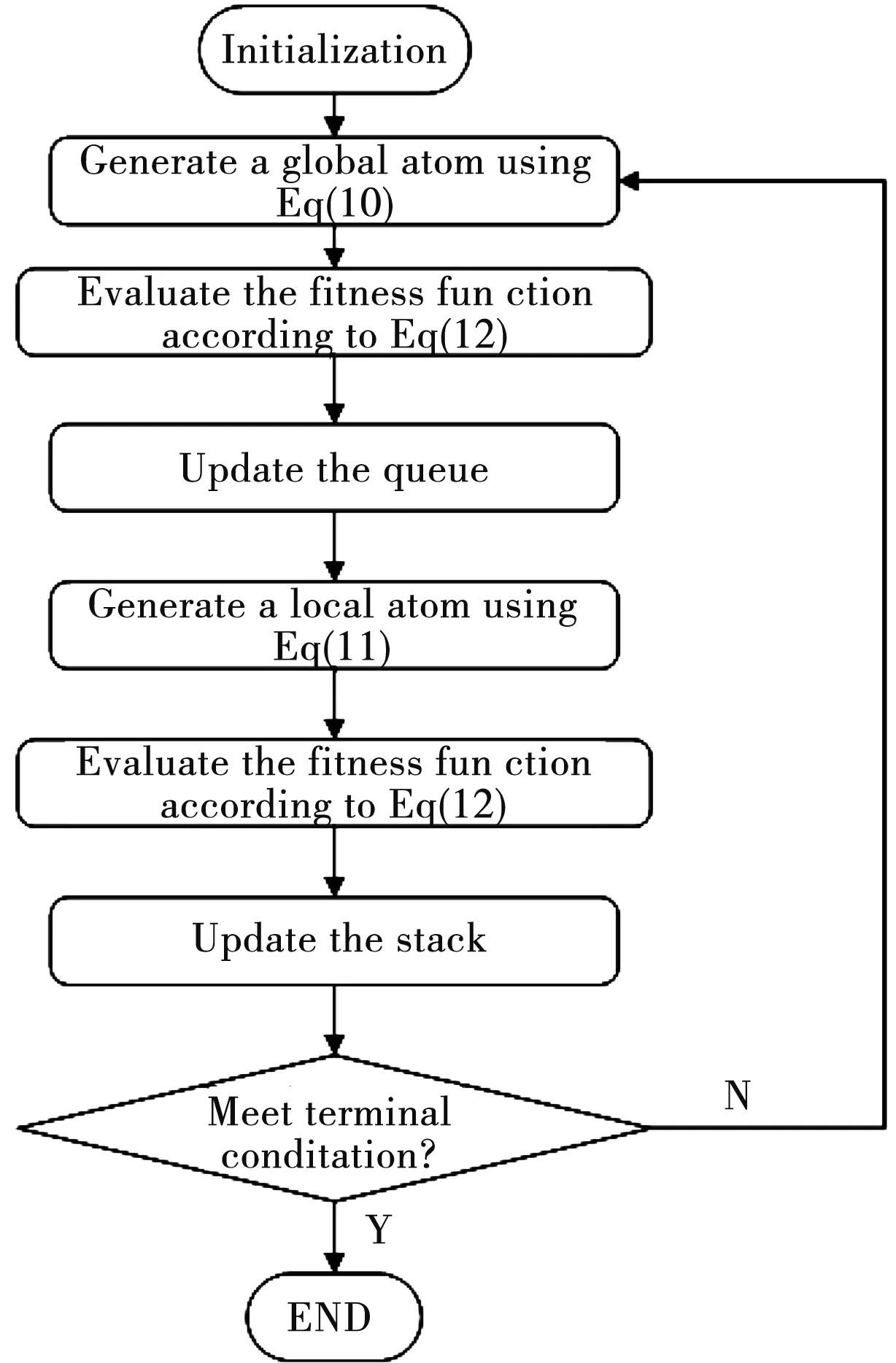
图2 用于露天矿运输调度优化的MOA算法流程图

(5)

表2 相关参数表

式(5)是一个关于μ的指数衰减函数，迭代初期，由于可行解的个数较少，甚至没有，则μ=0惩罚函数较大，也就是说惩罚力度较大，这时适应度函数的目的在于找到可行解；随着迭代次数的增加，可行解也逐渐增多，值也由0逐渐变大，惩罚力度变小，适应度函数逐渐将目标转向寻找目标函数；当μ=1，意味着解空间里全是可行解，此时惩罚函数最小.

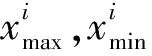
3 实例验证

现有某露天铁矿，具体参数见表2至表4，以总运量最小作为目标函数，建立该露天铁矿的运输调度模型.为验证算法的有效性，将MOA算法与精英保留策略的遗传算法(GA)[12]、自适应惯性权重粒子群算法(PSO-w)[13]和动态多群和声粒子群算法(DMS-PSO-HS)[14]进行比较，所有算法采用MATLAB2013a编程实现.所有的种群大小为135，最大迭代次数为300次，其中MOA算法数据结构为的上三角结构，局部区域搜索半径初始值设为2，随迭代次数线性减小.算法随机运行10次，所有实验结果都是取10次的平均值.

表3 各铲位矿石、岩石数量及矿石平均品位

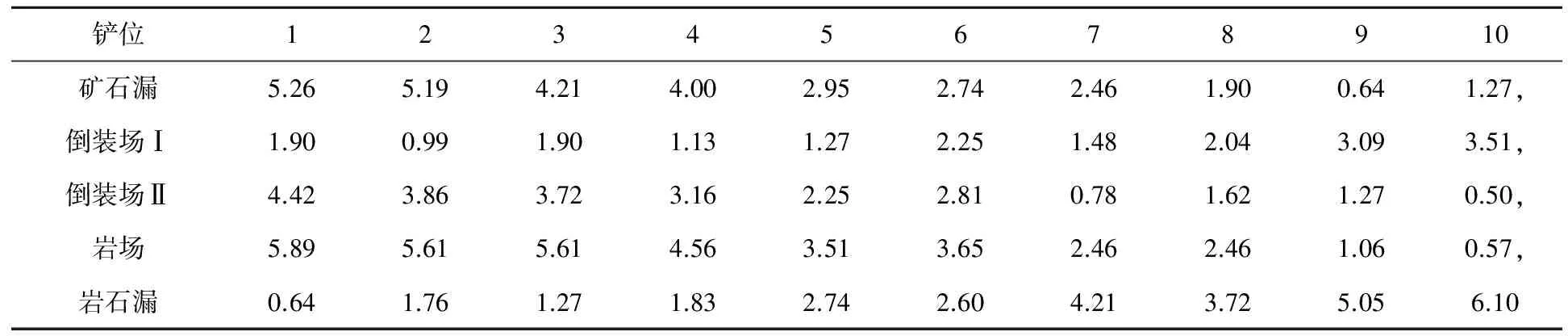
表4 各铲位与各卸点间的距离(km)

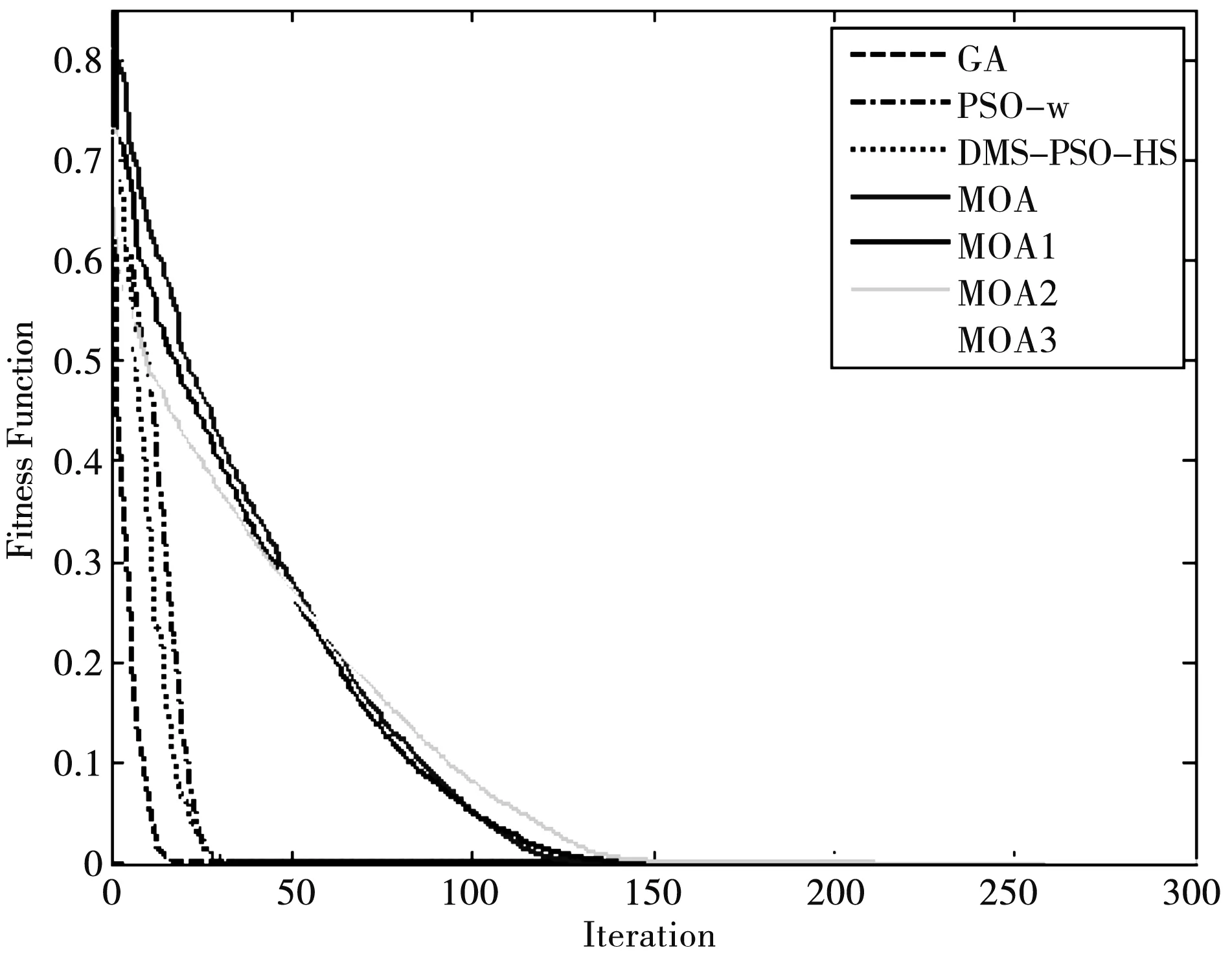
图3 适应度精度变化曲线图

图3为四种算法的优化过程适应度精度变化曲线图, 其中MOA1-MOA3表示由MOA算法得出的备选方案1至备选方案3.按照图1给出的MOA数据结构形式，MOA算法最多可以有14个备选方案，但由于越往后，总运量会越来越大，所以图中只给出了前3个备选方案和其他算法的最优方案进行比较.从图3可以看出GA、PSO-w和DMS-PSO-HS迭代次数在20次左右，适应度值就开始收敛，而MOA迭代约150次才开始收敛，MOA较其他3种算法的收敛速度会慢一些，但MOA的收敛精度却是最高的.

表5为寻优结果对比表，从表5可以看出，算法收敛精度由高到低依次是：MOA、DMS-PSO-HS、MOA1、MOA2、GA、PSO-w、MOA3，MOA算法的最优解收敛精度最高，，MOA算法的最优解收敛精度最高，这和从图3得到的结论是一致的，而且MOA算法得出的总运量也是最小的.此外MOA算法收敛速度和精度都优于文献[15]的结果.

表5 寻优结果对比

4 结论

实验结果表明，采用本文提出的方法进行露天矿统一运输调度的优化具有多重优势：(1) 自适应的惩罚函数参数少，结构简单，对问题依赖小，适应性强.(2) 能够提供多种备选方案.由于MOA算法特殊的数据结构特点，不仅能够保留算法找到的最优解，还能保留次优解的信息，充分利用过程信息.在实施露天矿运输调度时，如出现运输车辆出故障等某些条件临时发生变化又在可容忍范围之内时，可以考虑备选方案，以便能灵活、快速地调整运输调度计划，减少因临时变化给生产带来的损失.(3) 收敛稳定.MOA算法特殊的数据结构助于全局搜索和局部开发能力的平衡，而且在整个迭代过程中全局搜索和局部开发都同时存在，使得算法不至于过早收敛、跳出局部最优解的能力更强.(4) 精度高.MOA算法最优解的精度高于所选的其他几种群智能优化算法.虽然MOA算法的收敛速度不及其他几种算法，但在实际工程应用中，许多优化问题属于离线优化，这就意味着速度是次要的，而精度是第一位的.

本文提出的方法对露天矿统一运输调度优化是可行高效的，同时对露天矿统一运输调度优化问题进行多个备选方案的研究具有理论依据和实际意义.

[1] 宋子岭,白润才,魏春启.霍林河露天矿卡车调度决策方法及模型的研究[J].露天采煤技术,2001 (1)：38-41.

[2] 孙效玉,张维国.满足各种矿岩配车需求的露天矿车流规划模型[J].东北大学学报：自然科学版,2012, 33(10): 1 487-1 491.

[3] Rahmanpour M., Osanloo M. A genetic algorithm for pit limit and blending optimization[C]. //23rd International Mining Congress and Exhibition of Turkey, IMCET 2013,Turkey, 2013.

[4] 李勇,胡乃联,李国清.基于改进粒子群算法的露天矿运输调度优化[J].中国矿业,2013,22(4): 98-105.

[5] 胡乃联,李勇.李国清，等.用粒子群优化算法编制露天矿生产作业计划[J].北京科技大学学报,2013,35(4):537-543.

[6] V N Coelho a, M J F Souza a, I M Coelho, et al. Multi-objective approaches for the open-pit mining operational planning problem[J]. Electronic Notes in Discrete Mathemetics, 2012, 39: 233-242.

[7] Masoud Soleymani Shishvan a,c Javad Sattarvand. Long term production planning of open pit mines by ant colony optimization[J]. European Journal of Operational Research, 2015, 240: 825-836.

[8] Li Baolei, Shi Xinling, Gou Changxing, et al. Multivariant optimization algorithm for multimodal optimization [J]. Applied Mechanics and Materials, 2014, 483: 453-457.

[9] 李宝磊. 多元优化过程记忆算法及动静态条件下多模态寻优研究[D].云南昆明，云南大学，2015.

[10] 王军涛,尹国才,成岳鹏.智能算法在约束优化问题中的应用研究[J].北华航天工业学院学报,2013, 23(1):24-27.

[11] 甘敏,彭辉.一种新的自适应惩罚函数算法求解约束优化问题[J].信息与控制,2009,38(1):24-28.

[13] Shi Y, Eberhart R C. A modified particle swarm optimizer[C]. //Proceedings of IEEE World Congress on Computational Intelligence. NewYork, USA: IEEE, 1998.

[14] Zhao S Z, Suganthan P N, Pan Q K, et al. Dynamic multi-swarm particle swarm optimizer with harmony search[J]. Expert Systems with Applications, 2011, 38(4): 3 735-3 742.

[15] 霍晓宇,杨仕教,吴长振，等. 露天矿山运输调度系统粒子群优化[J]. 煤炭学报, 2012.37: 234-239.

VariousAlternativesforOptimizationofOpen-pit-mineIntegratedFleetHaulageDispatching

TIAN Qian-yi

(School of Computer Science, Minnan Normal University, Zhangzhou 363000，China)

By the condition limitation, the optimization of the open-pit-mine integrated fleet haulage dispatching has many complex constraints hard to deal with and yearns for various alternatives. A novel method of optimization that handles the complex constraints with an adaptive penalty function and optimizing with multivariant optimization algorithm is proposed. The adaptive penalty function is made up of simple and fewer parameters and is adaptable. The search individuals of multivariant optimization algorithm are constructed by a special data structure that is providing memory and information sharing according to different functions. Then the search individuals made full use of optimization process information, and implemented process memorise. At last the optimum could be found meanwhile various alternatives retention. A case study is performed by taking an open-pit iron mine as an engineering background. By comparing the optimization results of the algorithm with GA, PSO-w, DMS-PSO-HS, it was proved that the proposed method is simple and efficient to deal with the constraints, provides various alternatives and has advantages in the solutions’ quality for optimization open-pit-mine integrated fleet haulage dispatching. The various alternatives research of optimization open-pit-mine integrated fleet haulage dispatching has theory basis and practical significance. It is effective to optimize open-pit-mine integrated fleet haulage dispatching using the proposed method.

open-pit-mine，penalty function，multivariant optimization algorithm，search atom，process memorise

2017-05-28

福建省省属高校科研专项项目(JK2016025)；福建省教育厅产学研项目(JAT160283)；福建省中青年教师教育科研项目(JAS151296)资助

田谦益，E-mail：qytian@126.com.

TP183; TD561

A

1672-6634(2017)03-0088-05