人工蜂群优化及其在资源管理中的应用①

李俊青 王 永 桑红燕 高开周 韩玉艳 孟 涛

(1.聊城大学 计算机学院，山东 聊城 252059；2.山东师范大学 信息科学与工程学院，山东 济南 250014)

人工蜂群优化及其在资源管理中的应用①

李俊青1,2王 永1桑红燕1高开周1韩玉艳1孟 涛1

(1.聊城大学 计算机学院，山东 聊城 252059；2.山东师范大学 信息科学与工程学院，山东 济南 250014)

近年来，各种智能优化算法得到了广泛推广和应用，人工蜂群优化作为其中的一种典型算法被成功应用到工业界和制造业，譬如求解钢铁生产调度问题、供应链优化过程、交通问题等.本文首先对人工蜂群优化算法进行描述，并分析了该算法的收敛性.其次，对人工蜂群优化算法在各个领域的应用进行归类总结.最后，分析了讨论了人工蜂群优化如何应用于教学设计，以推动人工智能在教学改革中的应用.

人工蜂群优化，智能优化算法，收敛性，教学设计

0 引言

人工蜂群算法是由Karaboga等[1]于2005年提出的一种新的群体智能优化算法，是模拟蜜蜂寻找食物的过程而演化的仿生过程.自2005以来，ABC算法已被应用于求解许多优化问题[1-4].在基本ABC中，食物源(food source)和人工蜜蜂(artificial bees)是基本构成要素.人工蜜蜂又被分为三种[1-4]，即雇佣蜂(Employed bees)、跟随蜂(Onlooker bees)和侦察蜂(Scout bees).雇佣蜂的任务是在随机食物源周围进一步挖掘，以便找到更好的食物源；在雇佣蜂把挖掘后的信息带回后，守在蜂巢中的跟随蜂按照一定概率选择较好的食物，进一步搜索挖掘；当某些食物在经过一定周期后，未曾发生改变，则派出侦察蜂随机搜索新的食物源.

在2015世界机器人大会开幕时，习近平总书记明确指出，要将机器人和智能制造纳入优先重点领域，加强同各国科技界、产业界的合作，推动机器人科技研发和产业化进程，使机器人科技及其产品更好为推动发展、造福人民服务[5].人工蜂群优化算法作为人工智能领域中的典型算法已经越来越得到关注和推广.本文首先对人工蜂群优化算法进行描述，并分析了该算法的收敛性.其次，对人工蜂群优化算法在各个领域的应用进行归类总结.最后，分析了讨论了人工蜂群优化如何应用于教学设计，以推动人工智能在教学改革中的应用.

1 基本人工蜂群算法

1.1 ABC控制参数

ABC算法中基本控制参数包括：解集大小SN，解无更新而被丢弃的周期大小Ls，雇佣蜂数目Es，跟随蜂数目Os，侦察蜂数目Ss和终止条件[1-4].

1.2 初始解集

(1)

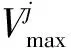
1.3 局部搜索策略

雇佣蜂和跟随蜂采用局部搜索进行食物源的搜索挖掘，基本ABC中局部搜索策略为：随机找到两个食物源i和k，计算两个食物源在第j维度的差值作为更新的部分，其具体计算公式

(2)

其中k∈{1,2,…,SN}∧i≠k.

1.4 全局搜索策略

守候在蜂巢中的跟随蜂通过轮盘赌注方法，选择较好的搜索空间继续进行食物源搜索，其计算公式如

(3)

其中fi表示第i个食物源目标值的大小.

2 基本ABC算法收敛性分析

2.1 算法的收敛准则

以下给出算法的收敛准则[6,7].

定义1 给定一个目标函数f，其解空间是从Rn到R，S是Rn的一个子集.在S中 某个点z，使得f的值最小化或者至少能够产生函数f的一个可接受的近似最优解.

假设1f(H(z,ξ))≤f(z),如果ζ∈S，则f(H(z,ξ))≤f(ξ).其中H是产生一个邻域解的函数.上述假设保证采用H函数产生的新的个体优于当前个体.

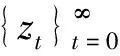
2.2 基本人工蜂群算法的收敛性分析

文献[6]证明了在基本人工蜂群算法中，存在以下定理：

定理2 蜂群状态序列{H(t);t≥0}是有限齐次Markov链.

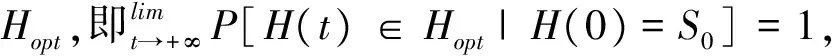
3 人工蜂群算法研究进展

3.1 针对连续优化问题求解

Karaboga和Basturk[1]针对多维数值优化问题，对比了ABC、DE、PSO和EA等多种算法，验证了ABC方法的有效性.Kang等[8]融合标准单纯形算法和ABC算法，用于求解反演分析问题(inverse analysis problem).Alatas[9]针对全局数值优化问题，给出了混沌ABC算法求解.Omkar等[10]给出了一种多目标ABC优化算法，用于求解组合结构的设计问题.Karaboga和Akay[11]针对约束优化问题，给出了改进的ABC算法.Akay和Karaboga[12]设计了一种改进的ABC算法，用于求解实参优化问题.研究表明，基本ABC算法主要应用于求解连续优化问题，如何采用ABC算法解决离散优化问题是一个研究热点.

3.2 针对算法改进

Banharnsakun等[13]改进了基本ABC算法中的跟随蜂策略，全局最好解用于在全体解中共享，以提高算法收敛能力.同时，每次迭代过程中，调整蜜蜂的搜索范围半径，提高了算法全局搜索的能力.Karaboga和Ozturk[14]针对ABC算法进行聚类分析，验证了算法的收敛能力.Ozturk等[30]结合遗传算子，改进了ABC算法的收敛能力和搜索性能.

3.3 针对优化调度问题求解

近年来，ABC算法被广泛用于求解各种优化调度问题，典型的应用包括资源有限的项目调度问题[15]、带有时间窗的旅行商问题[16]、低空航空器目标识别问题[17]、无人作战飞行器路径规划问题[18]、可靠性冗余分配问题[19]、设计和制造中的鲁棒优化问题[20]等.

在求解车间调度问题中，ABC算法也得到了一定应用.Huang和Lin[21]针对开放车间调度问题，给出了基于空闲时间过滤机制的ABC算法.Pan等[22]给出了自适应邻域结构的ABC算法框架；Sang等[23]研究了最小化总流经时间的批量流水线调度问题；Al-Salamah[24]则针对不同批次大小的单机批量调度问题，给出了基于约束二进制的ABC算法.针对柔性作业车间调度问题：文[25]设计了一种多目标ABC优化算法；进一步，Li等[26]给出了基于Pareto文档集的多目标ABC算法，用于求解带设备维修约束的FJSP问题；Gao等[27]则研究了带有订单插入的FJSP问题.晏晓辉等[28]则针对铜板带熔铸作业调度问题，给出了一种多目标ABC算法.Sundar等[39]针对无等待作业车间调度问题，给出了多种邻域结构的ABC算法.

4 人工蜂群优化在资源管理中的应用

4.1 人工蜂群优化在排课设计中的应用

排课是教学中的一项非常重要的工作，涉及学生、教室、教师等多种因素，包含诸多约束条件和目标，因而复杂的排课任务可以认为是一种NP难问题[30].解决此类问题的有效方法包括确定性算法，譬如分支定界方法、迭代搜索算法等.随着智能优化算法的推广和应用[30,31]，元启发式方法在排课系统中得到了越来越多的应用和推广，如粒子群优化算法[31]、离散型荧火虫算法[32]等.

通常，排课系统的主要约束包括：一位教师同一基本教学时间段只能在一个班级上课；一个班级在同一基本教学时间段只能上一位教师的课；一个教室在同一基本教学时间段只能有一个教师上课.另外，由于个别教师的特殊要求，还需要加入一些软约束条件，譬如，重要的专业课程最好安排在黄金时间段，教师不要连续长时间教授课程等.优化的目标是教师的满意度、学生的满意度达到最大化，同时满足各项约束条件.

采用人工蜂群优化算法设计排课系统，核心工作如下：(1) 编码问题.本文给出的方法是，建立两个向量，即课程向量和教师向量.课程向量以课程代号为编码基本元素，课程代号的有序排列作为排课系统的一个既定方案，如{C1,C2,C3,…,Cm}代表m门课的一个排列次序，即一个课程向量.教师向量以教师编号为编码基本元素，如{T1,T2,T3,…,Tn}，代表n位教师的一个排列次序，即一个教师向量.(2) 解码方案.解码的基本过程是，从课程向量中提取一门课，对应位置选择一位教师，从空闲教室中选择一个教室.但上述解码过程中，有可能存在非法编码问题，如对应的教师无法胜任所选的课程.此时，应该融合修复方案，即选择另外一个教师选择这门课程.(3) 进化策略.人工蜂群优化的关键进化过程主要取决于其局部搜索的过程，因而设计局部搜索策略对算法优化的过程影响较大.针对上述两向量编码方式，主要考虑采用三种局部搜索算子，即交换(swap)、插入(insert)、逆转(reverse).其中swap算子用于交换向量中任意选择的两个元素，insert用于把向量中任选的元素插入到不同的位置，reverse算子用于把向量中任选的两个不同位置的全部元素逆序排列.通过上述操作算子，蜂群中的一个解变成另一个解，进而更新并进化寻优.(4) 精英保留策略.通过进化，保留蜂群中最优的个体，使得系统进化朝理想的求解区域.(5) 跳出局部最优能力.由于优化算法的固有特性，往往无法跳出局部最优，即算法搜索到一定阶段后，易出现“早熟”的现象.针对这类问题，可以设计与禁忌搜索算法、模拟退火算法相结合的策略，进而提高算法全局搜索的能力.

4.2 人工蜂群优化在教学资源管理中的应用

目前，各类教学资源呈爆炸式增长，如何在大数据时代搜索合适的教学资源，进而更有利于教学开展，已经成为当前研究的热点.在大数据背景下，教学资源往往分布在各个节点，资源的分布性决定了资源共享需要考虑节点的分布性、资源的实时更新性、资源的有效性、资源的可用性，同时应满足用户需求最大化、经济指标最小化等目标，是一个多约束、多目标、动态的优化过程.基于此，人工蜂群优化适合于在教学资源共享、教学资源推荐等教学设计中应用和推广，搭建一种基于人工智能优化算法的教学资源共享、推荐平台，使得教学资源的使用、推荐过程实现自动化、智能化.

4.3 人工蜂群优化在新工科建设中的应用

新工科建设是工科类院校发展的方向，新工科建设特别强调学生的数据跟踪，譬如，大学生在大学阶段的课程成绩跟踪、毕业就业跟踪等.设计一种自动跟踪和优化平台，必定有力促进新工科建设.在云计算平台下，采用Hadoop、Map/Reduce管理和存储大数据，采用数据挖掘算法开展数据清洗、知识抽取及数据聚类，采用人工蜂群优化算法进行数据分析和优化，采用可视化技术进行数据展示，进而实现一种大学生学业、毕业、就业等大数据自动化跟踪平台.

5 结束语

人工蜂群算法近年来得到了广泛关注，在各个应用领域证明了该算法的有效性.在今后的推广和应用中，应注重以下几个方面的研究：(1) 目前对人工蜂群算法的改进，仅局限于针对连续优化问题的改进.如何改进ABC算法，使之更好地优化离散问题，亟待有效解决；(2) 应用ABC算法求解调度问题方面，如何结合问题特征，分析问题先验知识，设计自适应的算法框架，尚待进一步研究；(3) 针对离散优化调度问题，如何结合实际生产约束尚缺乏综合考虑，因而无法直接应用于求解现实调度问题.结合实际生产约束，挖掘问题特征、约束条件、目标特点，进而设计适合问题的优化算法框架，是进一步研究的热点；(4) 如何应用人工蜂群算法，提高教学改革的效果是进一步研究的热点.譬如，采用人工蜂群算法用于教学中的大数据分析、资源共享等.

[1] Karaboga D. An idea based on honey bee swarm for numerical optimization[R]. Technical Report TR06, Erciyes University, Engineering Faculty, Computer Engineering Department, 2005.

[2] Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687-697.

[3] Karaboga D, Akay B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108-132.

[4] Karaboga N. A new design method based on artificial bee colony algorithm for digital IIR filters[J]. Journal of the Franklin Institute, 2009, 346(4): 328-348.

[5] 习近平.将机器人和智能制造纳入优先重点领域[EB/OL]. http://news.sohu.com/20151124/n427789699.shtml.

[6] Rudolph G. Convergence analysis of canonical genetic algorithms[J]. IEEE Transactions on Neural Networks, 1994, 5(1): 96-101.

[7] 徐宗本. 计算智能中的仿生学理论与算法[M]. 北京: 科学出版社, 2003.

[8] Kang F, Li J, Xu Q. Structural inverse analysis by hybrid simplex artificial bee colony algorithms[J]. Computers & Structures, 2009, 87(13): 861-870.

[9] Alatas B. Chaotic bee colony algorithms for global numerical optimization[J]. Expert Systems with Applications, 2010, 37(8): 5 682-5 687.

[10] Omkar S N, Senthilnath J, Khandelwal R, et al. Artificial Bee Colony (ABC) for multi-objective design optimization of composite structures[J]. Applied Soft Computing, 2011, 11(1): 489-499.

[11] Karaboga D, Akay B. A modified artificial bee colony (ABC) algorithm for constrained optimization problems[J]. Applied Soft Computing, 2011, 11(3): 3 021-3 031.

[12] Akay B, Karaboga D. A modified artificial bee colony algorithm for real-parameter optimization[J]. Information Sciences, 2012, 192: 120-142.

[13] Banharnsakun A, Achalakul T, Sirinaovakul B. The best-so-far selection in artificial bee colony algorithm[J]. Applied Soft Computing, 2011, 11(2): 2 888-2 901.

[14] Karaboga D, Ozturk C. A novel clustering approach: Artificial Bee Colony (ABC) algorithm[J]. Applied Soft Computing, 2011, 11(1): 652-657.

[15] Shi Y J, Qu F Z, Chen W, et al. An artificial bee colony with random key for resource-constrained project scheduling[C].//Life System Modeling and Intelligent Computing. Springer Berlin Heidelberg, 2010: 148-157.

[17] Xu C, Duan H. Artificial bee colony (ABC) optimized edge potential function (EPF) approach to target recognition for low-altitude aircraft[J]. Pattern Recognition Letters, 2010, 31(13): 1 759-1 772.

[18] Xu C, Duan H, Liu F. Chaotic artificial bee colony approach to Uninhabited Combat Air Vehicle (UCAV) path planning[J]. Aerospace Science and Technology, 2010, 14(8): 535-541.

[19] Yeh W C, Hsieh T J. Solving reliability redundancy allocation problems using an artificial bee colony algorithm[J]. Computers & Operations Research, 2011, 38(11): 1 465-1 473.

[20] Cui Z, Gu X. An improved discrete artificial bee colony algorithm to minimize the makespan on hybrid flow shop problems[J]. Neurocomputing, 2015, 148: 248-259.

[21] Huang Y M, Lin J C. A new bee colony optimization algorithm with idle-time-based filtering scheme for open shop-scheduling problems[J]. Expert Systems with Applications, 2011, 38(5): 5 438-5 447.

[22] Pan Q K, Tasgetiren M F, Suganthan P N, et al. A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J]. Information Sciences, 2011, 181(12): 2 455-2 468.

[23] Sang H, Gao L, Pan Q. Discrete artificial bee colony algorithm for lot-streaming flowshop with total flowtime minimization[J]. Chinese Journal of Mechanical Engineering, 2012, 25(5): 990-1 000.

[24] Al-Salamah M. Constrained binary artificial bee colony to minimize the makespan for single machine batch processing with non-identical job sizes[J]. Applied Soft Computing, 2015, 29: 379-385.

[25] Li J Q, Pan Q K, Tasgetiren M F. A discrete artificial bee colony algorithm for the multi-objective flexible job-shop scheduling problem with maintenance activities[J]. Applied Mathematical Modelling, 2014, 38(3): 1 111-1 132.

[26] Li J Q, Pan Q K, Gao K Z. Pareto-based discrete artificial bee colony algorithm for multi-objective flexible job shop scheduling problems[J]. The International Journal of Advanced Manufacturing Technology, 2011, 55(9-12): 1 159-1 169.

[27] Gao K Z, Suganthan P N, Chua T J, et al. A two-stage artificial bee colony algorithm scheduling flexible job-shop scheduling problem with new job insertion[J]. Expert Systems with Applications, 2015, 42(21): 7 652-7 663.

[28] 晏晓辉, 朱云龙, 张浩. 基于 MOABC/D 的铜板带熔铸作业调度优化[J]. 计算机集成制造系统, 2013, 19(10): 2 528-2 535.

[29] Sundar S, Suganthan P N, Jin C T, et al. A hybrid artificial bee colony algorithm for the job-shop scheduling problem with no-wait constraint[J]. Soft Computing, 2017, 21(5): 1 193-1 202.

[30] 江浩, 江兵. 基于改进粒子群优化算法的贝叶斯网络结构学习[J]. 聊城大学学报:自然科学版, 2015(1):83-87.

[31] 郑亚强. 基于布谷鸟搜索算法优化的正交小波多模盲均衡算法[J]. 聊城大学学报:自然科学版, 2014, 27(1):102-106.

ResearchonArtificialBeeColonyAlgorithmandItsApplicationsinResourceManagement

LI Jun-qing1,2WANG Yong1SANG Hong-yan1GAO Kai-zhou1HAN Yu-yan1MENG Tao1

(1.School of Computer Science, Liaocheng University, Liaocheng 252059, China； 2.School of Information Science and Engineering, Shandong Normal University, Jinan 250014,China)

During recent years, varieties of intelligent optimization algorithms have been developed and applied in many types of areas. As one of the modern intelligent optimization algorithm, the canonical artificial bee colony has also been proposed and applied in many industrial and manufactural fields, such as the iron-steel production scheduling problem, the supply chain optimization problem, and the traffic problems. In this study, firstly, the canonical artificial bee colony algorithm was described, and then the convergence ability was analyzed. Lastly, the applications of the artificial bee colony algorithm were classified and summarized. Lastly, the application of artificial bee colony algorithm in the instructional design is discussed, and which will propose the development of the artificial intelligence in the education reformation.

artificial bee colony algorithm,intelligent optimization algorithm,convergence ability,instructional design.

2017-05-20

国家自然科学基金项目(61773192)资助

李俊青,E-mail:1141231492@qq.com.

TP 391.4

A

1672-6634(2017)03-0083-05