基于模糊C均值聚类的工业企业经济效益评价①

卢怡青 王 晴 朱家明

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

基于模糊C均值聚类的工业企业经济效益评价①

卢怡青1王 晴1朱家明2

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

基于模糊C均值聚类算法，以安徽省的16个城市为研究对象，通过Matlab软件进行求解分析，对安徽省工业企业的经济效益进行了评价.得出的结论是：合肥市和芜湖市企业经济效益较好，滁州市和安庆市企业经济效益属于中等水平，其余城市属于较差水平.同时，对评价结果进行了分析，在此基础上提出了合理的政策性建议.最后，对模糊C均值聚类算法提出了不断优化和拓展应用到其它领域的设想.

模糊C均值聚类，经济效益，聚类结果，Matlab

0 引言

李振强[1](2011)将因子分析法应用于工业企业经济效益综合评价中去，从而使得复杂的问题简单化，对于促进企业未来的客观发展具有积极的作用，但是缺点是浓缩后因子的意义不能完全确定，而且会有一些信息没有被提取；郑婉萍[2](2013)通过构建模糊综合评价体系计算出了工业企业经济效益的综合得分和排名，并进行了相应的比较和评价，证明了模糊综合评价方法适用于企业经济效益的评价；汪衍[3](2016)应用了集对分析理论，构建了企业经济效益的联系隶属度评价模型，应用集对联系隶属度刻画待研究对象的实测样本指标与评价标准间的同异反关系，再结合权重综合即可对工业经济效益水平进行评价.

模糊聚类分析法的实质就是通过运用模糊集理论对数据进行分析，从而对样本进行分类，使相似的样本归为一类，方便进行相关研究.模糊聚类算法有很多种，但其中模糊C均值聚类算法近年来在很多领域的应用越来越广泛且较成功.模糊C均值聚类算法是在Ruspini定义的集合的模糊划分概念的基础上，最早由Dunn提出的一种最为直观和简单的模糊算法.在1971 年Bezdek又对该种算法的收敛性进行了证明，该种算法的优势在于能够处理大规模数据集[4].

但是从目前的相关文献来看，将模糊C均值聚类算法应用于城市工业企业效益评价的相关研究还不是很多.所以，本文将构建基于模糊C均值聚类分析算法的工业企业经济效益评价体系，因为工业企业的经济效益好坏本身具有模糊性，难以直接对评价指标进行评价，但是模糊评价法能够将定性与定量相结合起来，为工业企业经济效益评价提供一种比较客观可行的方法.

1 模糊C均值聚类算法

模糊C均值聚类算法就是把N个向量xi(i=1,2,…,N)分成c个模糊类，并求出每类的聚类中心，使得非相似性指标的目标函数能够达到最小[5].目标函数的表达式为

(1)

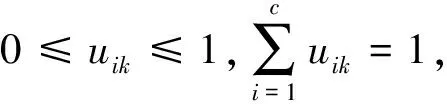
由拉格朗日乘数法构造新的目标函数，可求得使(1)式达到最小值的必要条件如(2)式所示[7].

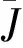
(2)

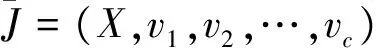
(3)

(4)

表1 2015年安徽省各个城市工业企业效益指标

2 实证分析

2.1 相关数据

为了将模糊C均值聚类算法应用于工业企业经济效益评价中去，本文选取了安徽省2015年16个城市工业企业的5个效益指标进行分析，选取效益指标分别是工业利润、亏损企业亏损额、净利润、工业利税和工业用电[9].相关数据详见表1.

2.2 模糊C聚类分析

采用模糊C均值聚类算法，利用MATLAB软件对表1的数据进行分析，求出各类的聚类中心[10].本文在分析时根据实际需要选择经济效益好坏分类数，采用三级评价，把各城市工业企业经济效益分为好、中、差三类.分析的具体结果详见表2.

(1) 三类聚类中心.(2) 对安徽省各城市工业企业经济效益进行类别划分，聚类结果详见表3.(3) Friedman 检验.Friedman检验是在多个配对样本来自的多个总体分布无显著差异的假设前提下，利用秩实现对多个总体分布是否存在显著差异的非参数检验方法[11].利用Matlab软件，对上述聚类的结果进行对各类别之间检验与其中任何两类合并后检验.检验结果表明其中两类合并后检验所接受的原假设比各类别之间的检验接受原假设要少，所以各类别之间的差异还是比较大的，而同一类中的个体差异较小.因此，聚类结果符合聚类的基本原则[12].

表2三类聚类中心

类别工业利润亏损企业亏损额净利润工业利税工业用电A0．58190．03410．54770．99170．1773B0．07100．02600．04500．14000．0723C0．31540．00790．30760．53060．1094

表3 聚类结果

2.3 聚类结果分析及政策性建议

本文所选取了安徽省16个城市的工业企业，对其经济效益进行评价.从聚类结果可以看出，安徽省的合肥市和芜湖市工业企业经济效益属于比较好的一类；滁州市和安庆市的工业企业经济效益属于中等水平一类；其它的12个城市的工业企业经济收益属于一类，和安徽省的其它城市相比经济收益较差.

合肥市作为安徽省的省会，近年来工业企业经济得到大力发展.电子信息、平板显示、汽车、装备制造和家电等属于合肥市的优势工业产业，所以企业要把握好发展的机遇，并在此基础上不断进行创新，推进传统工业企业改造升级，大力实施创新驱动发展战略.芜湖市是首批国家工业运行重点联系城市，其工业发展迅猛，发展质量效益大幅提升，规模企业不断扩大，企业如果要想获得更高的经济效益，要继续增强研发的能力，不断淘汰落后的工业产业，同时还需将工业与信息化进行更深一步的融合.

对于工业企业经济效益处于中等水平的滁州市和安庆市而言，要与经济效益发展较好的城市进行对比，找出在发展过程中存在的差距，根据本地的实际情况制定相关合理的发展政策，践行五大发展理念 坚持走绿色发展道路，不断提高工业企业经济效益.对于安徽省工业企业经济效益较差的城市来说，要加快园区发展和加强优势产业培育工作，主动把握和积极适应经济发展新常态，同时企业可以积极争取国家专项基金，加大节能环保改造，从而不断缩短与发展好的城市工业企业的差距，稳中求进[12].

3 结论和展望

3.1 结论

本文采用了模糊C均值聚类算法评价了工业企业的经济效益，以安徽省的16家城市为研究对象，将评价结果分成三类，最终得出的结论是：合肥市与芜湖时工业企业经济效益较好；滁州市和安庆市次之，属于中等水平；马鞍山等其它城市工业企业效益属于较差一类.在此基础上，又提出了适用于各个城市提高工业企业效益的政策性建议，如可以不断的进行改革创新；紧跟互联网时代的脚步，加快信息技术在企业生产经营各领域的应用；不断加快工业园区的发展等[13].模糊C均值聚类法给各城市工业企业经济效益的评价提供了新的思路，取得了较好的评价结果，具有积极的现实意义，为今后效益评价的研究提供了一定的参考[14].

3.2 展望

本文采用的模糊C均值聚类算法也存在些不足之处，该种算法容易出现陷入局部最小值，而得不到最优解的问题.所以，今后可以对模糊C均值聚类算法进行优化，提出一种更加有效的算法，如可以采用马氏距离度量取代原有的欧式距离度量，这样就可以避免了部分局部值[15].另外，由于本文是以安徽省的16个城市为研究对象，样本数不足够多，以后我们可以扩大研究范围，增加样本数，同时可以将经济效益评价结果细分，比如分成四类、五类等，从而使得企业效益评价结果更加明确.

在对数据进行挖掘分析时，模糊聚类分析法可以有效解决这一问题，因此人们对这一算法的关注度持续上升.接下来，我们要继续加强对模糊C聚类分析算法的研究，不断拓展，将其应用于更多的领域中.

[1] 李振强.浅析因子分析法在工业企业经济效益综合评价中的应用[J].经济视角：中旬刊,2011(10):112,177.

[2] 郑婉萍.我国各地区工业企业经济效益的模糊综合评价[J].科学决策,2013(12):40-54.

[3] 汪衍.基于联系隶属度的工业企业经济效益评价模型[J].中外企业家,2016(19):56-57.

[4] 崔西希.基于中智模糊C-均值聚类算法及其应用研究[D].西安：西安邮电大学,2017.

[5] 杨桂元.数学建模[M].3版,北京: 科学出版社,2014.

[6] 李凡.模糊C聚类综合评价法在企业财务信用评级中的应用[J].中国管理信息化,2011,(4):32-33.

[7] 秦国华.工业企业经济效益分析——以江苏省为例[J].当代会计,2017(5):78-79.

[8] 吴映程.工业企业的经济效益评价体系研究[J].中国管理信息化,2017,20(9):88-89.

[9] 刘莉.基于主成份分析法的西部地区工业企业经济效益综合评价[J].中小企业管理与科技：下旬刊,2012(1):169-170.

[10] 张萌.新型工业企业经济效益指标体系及其综合评价[J].企业导报,2016(9):16-17.

[11] 王国伟,闫丽,姚玉霞.基于熵权法加权的模糊C均值聚类算法研究[J].农业网络信息,2010(8):148-150.

[12] 李振强.浅析因子分析法在工业企业经济效益综合评价中的应用[J].经济视角：中旬,2011(10):112.

[13] 郑婉萍.我国各地区工业企业经济效益的模糊综合评价[J].科学决策,2013(12):40-54.

[14] 赵文睿.基于聚类分析的中国房地产企业信用评级实证研究[D].长春：吉林大学,2016.

[15] 熊拥军,刘卫国,欧鹏杰.模糊C-均值聚类算法的优化[J].计算机工程与应用,2015(11):124-128.

EvaluationoftheIndustrialEnterprises’EconomicBenefitBasedonFuzzyC-meansClustering

LU Yi-qing1WANG Qing1ZHU Jia-ming2

(1．School of Finance, Anhui University of Finance and Economics, Bengbu 233030, China; 2. School of Statistics and Applied Mathematics, Anhui University of Finance and Economics,Bengbu 233030, China)

Based on the fuzzy C-means clustering algorithm, 16 cities in Anhui Province were selected as the research object, and the economic benefits of industrial enterprises in Anhui Province were evaluated by Matlab software. The conclusion is that the economic benefits of enterprises in Hefei and Wuhu are better. The economic benefits of enterprises in Chuzhou and Anqing are medium and the other cities are the worst. At the same time, the evaluation results are analyzed, and on this basis, reasonable policy suggestions are put forward. Finally, put forward the idea of the fuzzy C-means clustering algorithm can be optimized and expand the application to other areas.

fuzzy C-means clustering,economic benefits,clustering results,Matlab

2017-03-05

国家自然科学基金项目(11601001)；国家级大学生创新创业训练计划(201610378418)资助

朱家明，E-mail:zhujm1973@163.com.

F014.35

A

1672-6634(2017)03-0075-04