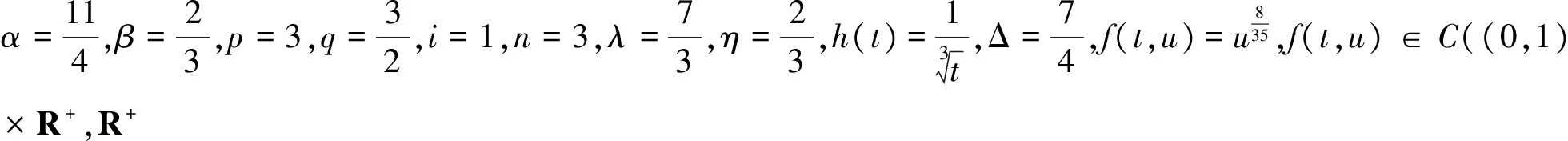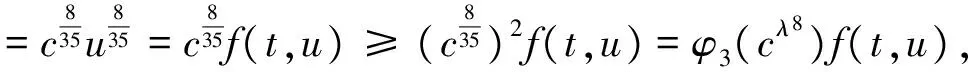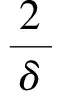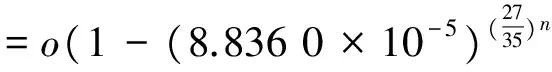含p-Laplacian算子高阶分数阶微分方程的唯一迭代正解①
2017-11-22仲秋艳张兴秋
仲秋艳 张兴秋
(1.济宁医学院 信息技术中心,山东 济宁 272067;2.济宁医学院 医学信息工程学院,山东 日照 276826)
含p-Laplacian算子高阶分数阶微分方程的唯一迭代正解①
仲秋艳1张兴秋2
(1.济宁医学院 信息技术中心,山东 济宁 272067;2.济宁医学院 医学信息工程学院,山东 日照 276826)
利用单调迭代技巧,得到了一类含p-Laplacian算子的高阶分数阶微分方程非局部问题迭代正解的唯一性结果,同时给出了解的迭代程序和误差估计.
分数阶方程, 单调迭代,p-Laplacian算子,正解,唯一性
0 引言
近年来,由于在复杂介质的电动力学、电磁学、聚合物流变学、分数控制系统与分数控制器、神经的分数模型以及分数回归模型等诸多方面的应用[1-3],分数阶微分方程的研究得到了广泛的关注和迅速的发展.文献[4-16],在不同的边值条件下,获得了分数阶非局部边值问题正解以及多个正解的存在性.
如何求出分数阶微分方程的正解在应用上具有重要的意义.本文主要目的是给出下列具有P-Laplacian算子和积分边值条件的分数阶微分方程(下称PFDE)
(1)
与文献[4-7]相比,本文具有以下特征:首先边值条件更加广泛;其次,微分方程含有P-Laplacian,这使得考虑的问题更加一般;最后,本文不但给出了解的存在性结果,而且给出了解的迭代程序及误差估计.显然,稍加修改,本文结果可用于含Riemann-Stieltjes积分的边值问题.
1 引理
有关分数阶微积分的基本定义和性质可在文献[1-4]找到,从略.

(2)
引理1[17]对y∈C[0,1],y≥0,(2)的唯一解为

其中
G(t,s)=G1(t,s)+G2(t,s),
(3)
(4)

(5)
显然,G(t,s)在[0,1]×[0,1]上连续.
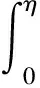
(a1)G(t,s)≥m1tα-1s(1-s)α-1-i,∀t,s∈[0,1];
(a2)G(t,s)≤M1tα-2s(1-s)α-1-i,∀t,s∈[0,1];
(a3)G(t,s)>M1tα-1(1-s)α-1-i,∀t,s∈[0,1];
(a4)G(t,s)>0,∀t,s∈(0,1);
2 主要结果
记e(t)=tα-1,本文使用以下条件.
(H)f∈C((0,1)×R+,R+),对于固定的t∈(0,1)以及c∈(0,1),f(t,u)关于u非减且存在常数0 f(t,cu)≥φp[c(1+η(c))]f(t,u), (6) 这里η(c)=m(c-r-1). 注1 如果c≥1,那么(6)式等价于 (7) 设E=C[0,1],令P={x∈C[0,1]∶x(t)≥0,t∈[0,1]}.则P是Banach空间E中正规常数为1的正规锥.定义E的子集D如下 D={u∈P∶存在正数lu<1 (8) 注意到e(t)∈P,易知D非空.定义算A如 (9) 定理1 设条件(H)满足.如果 (10) 那么PFDE(1)有唯一正解w*∈D,且存在常数 使得ke(t)≤w*(t)≤Ke(t),t∈[0,1], 证明首先证明算子A映D到D. 事实上,对任意u∈D,存在正数Lu>1>lu满足 lue(t)≤u(t)≤Lue(t),t∈[0,1]. (11) 由条件(H),引理2,(7),(10),(11)诸式得 (12) 及 (13) 这里, 令 于是 取 (14) 则0<δ<1.由(14)式得 [1+η(δ)]-1w0≤Aw0≤[1+η(δ)]w0. (15) un=Aun-1,vn=Avn-1,n=1,2,…, (16) 注意到f(t,u)关于u非减,由(6)和(7)两式得 (17) (18) 根据(15)-(18)诸式,我们有 u1=Au0≥δ[1+η(δ)]Aw0≥δw0=u0, (19) (20) 由(19)、(20)式,利用数学归纳法,我们有 u0≤u1≤…≤un≤…≤vn≤…≤v1≤v0. (21) 此外,由(17)式得 (22) 注意到u0=δ2v0,我们有 (23) 由于P为正规常数为1的正规锥,故对于任意正整数P,由un+p-un≤vn-un,我们有 (24) 即{un}是一个Cauchy列.于是un收敛于某w*∈D.显然 ‖vn-w*‖≤‖vn-un‖+‖un-w*‖, 结合(24)式,我们有vn→w*及un≤w*≤vn,故,un+1=Aun≤Aw*≤Avn=vn+1,n=1,2,…,令n→+∞取极限得w*=Aw*,即,w*∈D是A的一个不动点. 取初值w0=e(t), 则le≤Ae≤Le,这里 u1=Au0≥k[1+η(k)]Ae≥k[1+η(k)]le≥ke=u0, (25) v1=Av0≤K[1+η(K-1)]-1Ae≤K[1+η(K-1)]-1Le≤Ke=v0. (26) 根据(25)及(26)两式可知唯一解w*满足ke(t)≤w*(t)≤Ke(t),t∈[0,1]. (27) 下面在比条件(H)更强的条件下研究PFDE(1).列出以下条件: (H*)f∈C((0,1)×R+,R+),对于任意固定的t∈(0,1),c∈(0,1),f(t,u)关于u非减,且存在常数0<λ*<1使得对于任意(t,u)∈(0,1)×R+,f(t,cu)≥φp(cλ*)f(t,u). (H0)f∈C((0,1)×R+,R+),对于任意固定的t∈(0,1),c∈(0,1),f(t,u)关于u非减,且存在常数0<λ<1使得对于任意(t,u)∈(0,1)×R+,f(t,cu)≥cλf(t,u). (H1)f∈C(0,1)×R+,R+),存在常数0<λ1≤λ2<1使得对于任意(t,u)∈(0,1)×R+,cλ2f(t,u)≤f(t,cu)≤cλ1f(t,u),0 证由条件(H*),对任意c∈(0,1),(t,u)∈(0,1)×R+,我们有 f(t,cu)≥φp(cλ*)f(t,u)=φp(cc-1(1-λ*))f(t,u)≥φp[c(1+η(c))]f(t,u), 这里η(c)=m(c-r-1),m=1,r=1-λ*,于是,由定理1可证定理2. 注2 从定理2的证明过程可知,条件(H)弱于(H*).另外,由文献[12]注 3.4可知(H0)弱于(H1).文献[12],[14]利用条件(H0)研究微分方程解的存在唯一性,而文献[18-20]则利用条件(H1)研究某些整数阶微分方程正解存在的充要条件.易知当p>2时,(H*)弱于(H0). 考察下列分数阶微分方程 (28) [1] Samko S G, Kilbas A A, Marichev O I. Fractional Integral and Derivativs[C].//Theory and Applications. Gordon and Breach, Switzerland, 1993. [2] Podlubny I.Fractional Differential Equations[C].//Mathematics in science and Engineering.NewYork, London, Toronto: Academic Press, 1999. [3] Kilbas A A,Srivastava H M,TrujilloJ J.Theory and Applications of Fractional Differential Equationss[C]. //North-Holland Mathematics Studies. Elsevier Science B V Amsterdam, 2006. [4] Wang Yong-qing,Liu Li-shan,Wu Yong-hong. Positive solutions for a nonlocal fractional differential equation[J]. Nonlinear Anal, 2011, 74: 3 599-3 605. [5] Cabada A, Wang Guotao.Positive solutions of nonlinear fractional differential equations with integral boundary value conditions[J].J Math Anal App,2012,389:403-411. [6] Feng Mei-qiang, Zhang Xue-mei, Ge Wei-gao.New existence results for higher-order nonlinear fractional differential equation with integral boundary conditions[J].Boundary Value Problems,2011,2011:1-20. [7] Wang Lin,Zhang Xing-qiu.Existence of positive solutions for a class of higher-order nonlinear fractional differential equations with integral boundary conditions and a parameter[J].J Appl Math Comput, 2014, 44: 293-316. [8] Zhang Xing-qiu, Wang Lin Sun Qian. Existence of positive solutions for a class of nonlinear fractional differential equations with integral boundary conditions and a parameter[J]. Appl Math Comput, 2014, 226: 708-718. [9] Zhang Xin-guang, Liu Li-shan, Wu Yong-hong, et al. The iterative solutions of nonlinear fractional differential equations[J]. Appl Math Comput, 2013, 219: 4 680-4 691. [10] Li Shun-jie, Zhang Xin-guang,Wu Yong-hong,et al. Extremal solutions forp-Laplacian differential systems via iterative computation[J]. Appl Math Lett, 2013, 26:1 151-1 158. [11] Sun Yong-ping, Zhao Min. Positive solutions for a class of fractional differential equations with integral boundary conditions[J]. Appl Math Lett, 2014, 34: 17-21. [12] Zhang Xin-guang, Han Yue-feng. Existence and uniqueness of positive solutions for higher order nonlocal fractional differential equations[J]. Appl Math Lett, 2012, 25: 555-560. [13] Tian Yuan-sheng, Li Xiao-ping. Existence of positive solution to boundary value problem of fractional differential equations withp-Laplacian operator[J]. J Math Anal Appl, 2015, 47: 237-248. [14] 仲秋艳,张兴秋.一类具有p-Laplacian算子的奇异分数阶微分方程无穷点边值问题的正解[J]. 聊城大学学报:自然科学版,2016, 29(2):25-32. [15] Zhang Xing-qiu. Positive solutions for singular higher-order fractional differential equations with nonlocal conditions[J]. J Appl Math Comput, 2015, 49: 69-89. [16] Zhang Xin-guang, Liu Li-shan. A necessary and sufficient condition for positive solutions for fourth-order multi-point boundary value problems withp-Laplacian[J]. Nonlinear Anal, 2008, 68: 3 127-3 137. [17] 仲秋艳,张兴秋.含参数及p-Laplacian算子的奇异分数阶微分方程积分边值问题的正解[J].山东大学学报:理学版, 2016, 51(6): 78-84. [18] Wei Zhong-li. A necessary and sufficient condition for the existence of positive solutions of singular super-linearm-point boundary value problems[J]. Appl Math Comput, 2006, 179: 67-78. [19] Wei Zhong-li, Pang Chang-ci. The method of lower and upper solutions for fourth order singularm-point boundary value problems[J]. J Math Anal Appl, 2006, 322:675-692. [20] Wei Zhong-li.A class of fourth order singular boundary value problems[J].Appl Math Comput,2004, 153: 865-884. UniqueIterativePositiveSolutionforHigher-orderFractionalDifferentialEquationswithp-Laplacian ZHONG Qiu-yan ZHANG Xing-qiu (1.Department of Information Technology, Jining Medical College, Jining 272067, China; 2.School of Medical Information Engineering, Jining Medical College, Rizhao 276826, China) By means of monotone iterative technique, uniqueness results of positive solutions for a class of higher nonlocal fractional differential equations withp-Laplacian are obtained. The iterative sequences of solution and error estimation are also considered. fractional differential equations,monotone iterative technique,p-Laplacian, positive solution, uniqueness 2017-05-12 国家自然科学基金项目(11571296,11571197);山东省高校科技发展计划项目(J15LI16);山东省自然科学基金项目(ZR2015AL002)资助 张兴秋,E-mail:zhxq197508@163.com. O175.8 A 1672-6634(2017)03-0028-07
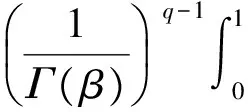
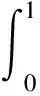


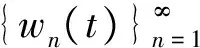


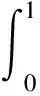
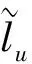

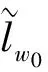





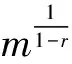

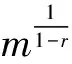
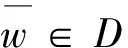

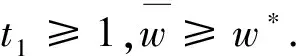

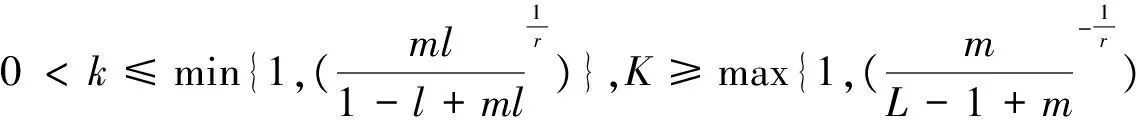
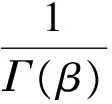
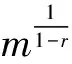
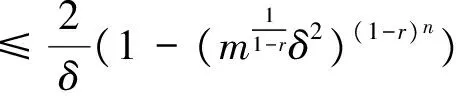


3 应用举例