直升机飞行动力学数学建模问题

陈仁良*,李攀,吴伟,孔卫红

南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016

直升机飞行动力学数学建模问题

陈仁良*,李攀,吴伟,孔卫红

南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016

直升机飞行动力学数学模型是飞行控制系统设计的基础,也是直升机飞行品质设计和评估的主要手段。直升机是一个多体系统,在直升机飞行动力学建模过程中,必须考虑旋翼、机体与升力面等的运动耦合、惯性耦合、结构耦合和气动耦合以及非定常、非线性特性,给出各个运动部件的物理模型及其数学表达形式,是对不同假设、子模型进行分析和综合的一个复杂的过程。鉴于此,简要回顾了单旋翼带尾桨直升机飞行动力学数学模型的研究现状,着重描述了直升机飞行动力学数学建模中的旋翼气动力建模、直升机气动干扰建模、旋翼/发动机建模以及直升机飞行动力学模型的集成与综合的研究现状与研究进展。最后,针对直升机飞行动力学的数学建模提出了今后的研究重点。

直升机;旋翼;飞行动力学;气动干扰;机动飞行

直升机飞行动力学数学建模是根据物理定律,采用直升机空气动力学等理论建立直升机运动、外力(矩)与操纵(控制)之间的关系。直升机飞行动力学数学模型是飞行控制系统设计的基础,也是直升机飞行品质设计和评估的主要手段。美国陆军最新颁布的“军用旋翼飞行器驾驶品质要求(ADS-33E-PRF)”明确规定新机型在各个研制阶段都需用直升机飞行动力学模型进行飞行品质的核查[1]。

直升机的飞行动力学数学建模比固定翼飞机要复杂许多,这是由直升机的特点决定的。

第一,旋翼不仅是直升机的升力面,也是直升机的操纵面,还是直升机的推进器[2]。除了偏航力矩来自尾桨,直升机操纵和推进所需的力和力矩都来自旋翼的气动力,即直升机的升力、操纵力(矩)和推进力是相互耦合的。对固定翼飞机而言,升力面是机翼,操纵面是升降舵、副翼以及方向舵,推进器是发动机(喷气、涡扇发动机)或螺旋桨(螺旋桨飞机),也就是说,固定翼飞机的升力面、操纵面和推进器是相对独立的。

第二,旋翼的空气动力现象非常复杂[3],直升机旋翼由大展弦比的柔性桨叶组成,依靠自身的旋转运动来产生升力。旋翼的空气动力现象具有两个显著的特点:一是桨叶附近在某些飞行状态下的分离流、激波等高度非线性的流动现象,其中分离流导致的非线性失速以及激波引起的波阻给旋翼气动分析带来了很大困难。二是桨叶后缘拖出的尾涡在桨尖附近迅速卷起,形成以桨尖涡为主导的旋翼尾迹,在悬停及小速度前飞状态,由于来流速度很小,桨尖涡滞留在桨盘附近,引起严重的几何形状畸变,在桨盘平面诱导强烈的非均匀入流,改变桨叶的气动载荷分布和桨叶的运动,从而影响直升机的平衡特性和操稳特性;反过来,桨叶气动载荷分布和桨叶运动的变化,又会影响旋翼尾涡的强度分布及几何结构的变化,旋翼尾迹、桨叶运动及桨叶气动载荷三者之间形成一个高度耦合的复杂动力系统。当直升机作机动飞行时,旋翼的整体运动以及桨叶上的分布哥氏力将改变三者的耦合动力学行为,是一个存在惯性、结构和气动耦合的复杂动力学系统。长期以来,旋翼的气动力建模一直是直升机飞行动力学建模的关键和核心。

第三,旋翼与其他气动部件之间的气动干扰是直升机飞行动力学数学建模中面临的另一个关键问题[4],尤其在悬停、小速度前飞状态下,旋翼尾迹冲刷到机身、尾翼和尾桨等部件,影响这些部件的空气动力,反过来机身等部件影响旋翼尾迹,引起旋翼气动力的变化。

与固定翼飞机相比,直升机各部件之间的气动干扰有其特殊性,这是由旋翼流场特性和直升机构型决定的。首先,旋翼流场本身包含了非定常性、非线性和三维效应等多种复杂空气动力学特征,流场中桨尖涡结构,涡桨干扰、桨叶局部区域的动力分离及前行桨叶桨尖部位周期性的跨声速运动,拖曳涡和脱离涡复杂的运动轨迹和形状等。其次,直升机的构型与固定翼飞机有本质的区别,气动干扰的原理和方式不同,直升机的旋翼和尾桨都产生旋转气流,不仅运动复杂,而且还会引起相互干扰,再加上与直升机其他部件的相互作用,使气流流动变得更加复杂。

直升机飞行动力学数学建模主要涉及旋翼、尾桨、机身、平尾和垂尾等部件的气动力建模以及旋翼/发动机耦合动力学建模,对于机动飞行而言,还需要建立旋翼桨叶的耦合动力学与运动学模型[5]。针对结构和气动力复杂、涉及多学科交叉的直升机进行飞行动力学数学建模,不仅要对数学建模方法进行选择和改进,而且要根据实际情况进行抽象和概括,通过综合与集成的方法使直升机复杂的系统构成有机的整体。

本文针对单旋翼带尾桨直升机飞行动力学数学建模中的关键问题开展讨论,重点讨论旋翼气动力建模、直升机旋翼与其他部件之间的气动干扰建模、旋翼/发动机耦合动力学建模以及直升机飞行动力学模型的集成与综合等问题,提出这些建模方法的现状及发展趋势,供相关人员参考。

1 直升机飞行动力学建模简要回顾

直升机飞行动力学数学模型经历了从简单的刚体六自由度动力学模型向复杂多自由度模型的发展过程,研究对象由直升机定常飞行向机动飞行研究的发展。

直升机刚体六自由度飞行动力学模型借鉴了固定翼飞机的飞行动力学建模方法,通过对刚体六自由度动力学模型的线化(平衡点处)得到直升机线性飞行动力学模型,然后借助完整的线性系统理论和方法研究直升机的飞行特性,能方便地给出直升机的一些基本操稳特征,服务于直升机总体设计和飞行控制系统设计[6-9],理论和实践证明,直升机飞行动力学的线性模型仅适用于机动性要求不高的运输型直升机,用于武装直升机的机动飞行时会引起较大的误差。

由于旋翼、机体、尾面、尾桨的气动耦合和直升机的运动、结构及惯性耦合,直升机的运动具有明显的非线性特性[10-14]。直升机的运动非线性问题早已引起诸多研究者的重视,已经发展了许多用于理论分析[15-18]、工程数值模拟[19-22]和地面实时仿真的直升机数学模型[23-27],文献[28-31]对此作了比较详细的分析和系统的归类。

现有两种形式的直升机飞行动力学非线性数学模型。第1种是描述直升机运动的微分方程组本身的非线性,与系统中各子系统(如旋翼模型、各部件的动力学模型)的线性和非线性没有直接的关系。建立这种模型的主要出发点是为直升机飞行控制系统设计提供相对准确、可靠的对象特性。其典型代表是ARMCOP模型[17-18]。该模型为低阶模型,采用静态入流模型,用叶素理论求出旋翼的周期平均力和力矩,适用于旋翼系统的设计与分析,自该模型建立以来,已有多种改进版本[20-21]。

第2种模型不仅包括运动微分方程组本身的非线性,还包含了模型中各子系统的非线性。直升机的飞行仿真是建立这种模型的主要出发点,美国Sikorsky直升机公司开发的GENHEL模型[22]为这一类模型的典型代表。该模型仍然假设机身为刚性,但除了机体运动的6个刚体运动自由度外,还加入旋翼运动自由度,包括桨叶挥舞、摆振运动自由度以及旋翼转速自由度,并采用经验公式修正桨叶扭转运动。旋翼气动力模型中采用静态非均匀入流模型,用叶素理论逐段积分计算桨叶的气动力,考虑旋翼下洗流对机身、尾翼与尾桨的下洗效应及机身对尾翼、尾桨的侧洗效应。机身和尾面气动力采用大范围迎角和侧滑角的非线性风洞试验数据。通过不断完善,该模型日趋成熟,已广泛用于地面实时数值仿真[23]、非线性方程并行处理方法研究[24]及高阶线性模型简化[25]等研究。值得指出的是,为了引入旋翼转速自由度,GENHEL模型建立了发动机/燃油调节系统模型以及发动机/燃油调节系统/旋翼动力学耦合模型。

GENHEL模型在中等飞行速度有较高的置信度,但在低速、大速度飞行及机动飞行状态的准确度有待进一步提高,原因是人们对旋翼流场以及旋翼/机身/尾面/尾桨之间气动干扰的复杂性认识有待进一步提高。文献[20]及文献[32-35]所建立的模型也存在上述现象,与GENHEL模型同时期的Takahashi模型[35]计算得到的稳定平飞状态旋翼总距配平结果与飞行测量数据[36]之间的误差在悬停、低速以及大速度飞行状态较大,如图1所示,图中V为前飞速度,δc为总距杆位置。对于机动飞行,则出现直升机异轴响应与飞行实测结果的反号问题。以UH-60A直升机悬停时施加横向压杆为例,不论是GENHEL模型,还是Zhao和Curtiss模型[34],或者Takahashi模型,得到的直升机俯仰角速度响应(异轴响应)均与飞行实测得到的结果方向相反,如图2和图3所示,图中t为时间,q为俯仰角速度。异轴响应的反号问题是直升机飞行动力学模型存在的普遍问题,除了UH-60A直升机,用上述模型对BO-105以及AH-64计算直升机动态响应时也出现了类似的现象[37-38]。

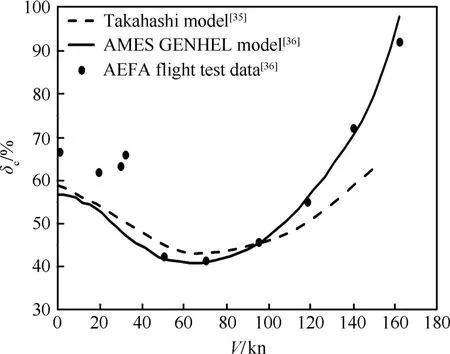
图1 总距预测结果与飞行试验数据的对比Fig.1 Comparison of collective pitch prediction with flight test data

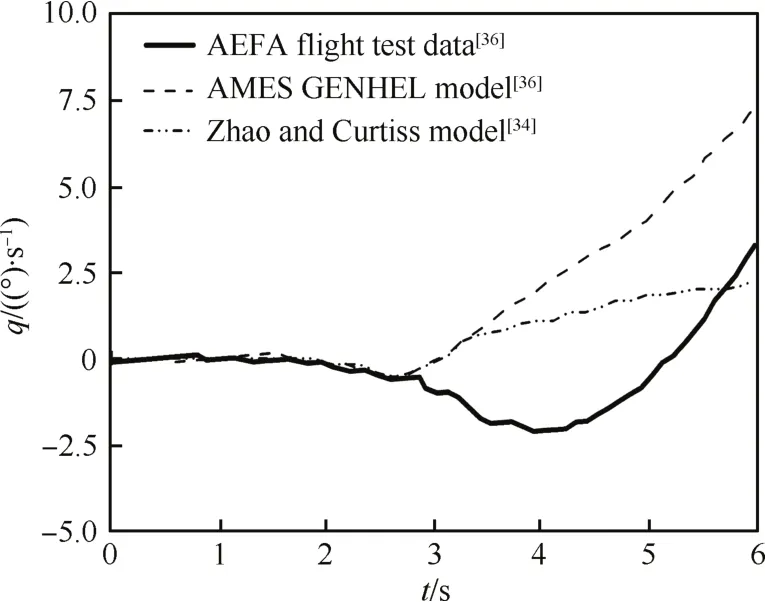
图2 GENHEL、Zhao和Curtiss模型与飞行试验数据的对比Fig.2 Comparison of models of GENHEL,Zhao and Curtiss with flight test data

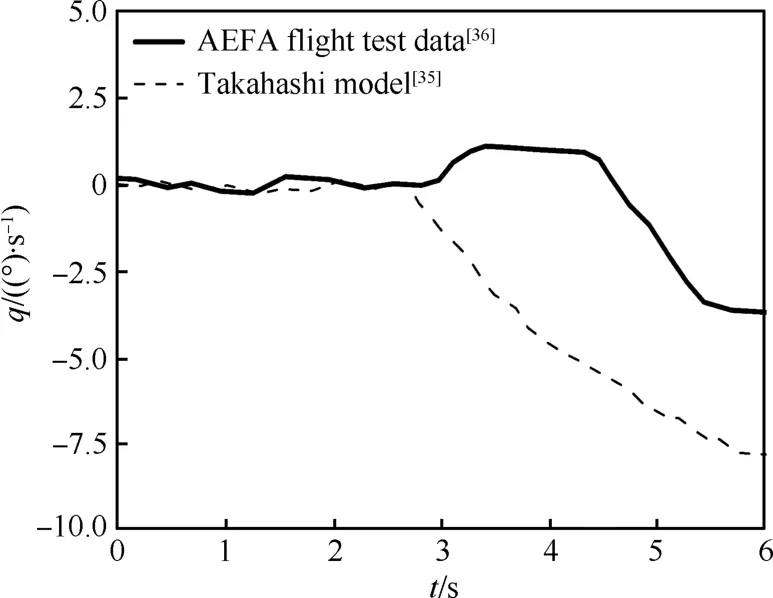
图3 Takahashi模型与飞行试验数据的对比Fig.3 Comparison of Takahashi model with flight test data

除了GENHEL模型,诸多学者出于不同的研究目的以及不同型号的建模需要,建立了许多直升机飞行动力学模型[39-49],这些模型的精度与GENHEL大致相当。

为了进一步提高直升机飞行动力学模型的置信度,国内外研究者围绕旋翼气动力模型、桨叶动力学模型、非定常旋翼尾迹模型以及二维翼型非定常气动力模型的综合与集成开展研究[50-55]。旋翼桨叶气动载荷计算计入翼型气动力非定常和动态失速特性的影响,桨叶动力学模型采用基于有限元分析的弹性桨叶模型,并将先进的旋翼自由尾迹模型应用到直升机飞行动力学机理建模中。

随着武装直升机的出现,直升机的机动飞行渐渐成为人们研究的热点。最初的研究是通过飞行试验来探索直升机在稳态机动过程中的基本特性和机动飞行的潜力,随后尝试机动性能及其极限的飞行研究[56-57],包括直升机的加减速性能、转弯性能以及俯冲拉起性能。这些飞行试验为后续理论研究提供了丰富的验证数据。

在理论研究方面,能量法是早期直升机机动飞行研究的主要方法,该方法基于能量守恒来计算直升机机动飞行的轨迹,由于能量法只关注能量转换,对能量转换的实际条件和具体情况难以细究,因而用能量法得到的结果可信度低[58-62]。20世纪80年代后期出现了约束轨迹的直升机机动飞行逆解方法[63-64],该方法由英国格拉斯哥大学的Thomson和Bradley提出[63],逆解方法针对特定的机动科目对其飞行轨迹进行数学描述,然后通过反求飞行动力学方程组来获得该机动科目的操纵量。该方法虽然成功运用在直升机机动飞行的研究中,并取得了相应的研究成果,但由于该方法是根据描述的飞行轨迹确定所需的操纵规律,属于求解直升机飞行动力学方程的逆问题,理论上存在多个求解结果,加上直升机飞行动力学模型的复杂性,在实际应用时尚有不少困难,如何研究直升机机动飞行的求解方法仍是以后研究工作的重点。

2 直升机飞行动力学数学建模方法的发展

直升机飞行动力学数学建模涉及旋翼气动力建模、直升机气动干扰建模、发动机建模以及机动飞行建模等方面,本节将阐述上述模型的建模技术及进展。

2.1 旋翼气动力建模

旋翼是直升机的升力面、操纵面和推进器,这就决定了它具有一系列复杂的空气动力特性。

在直升机的飞行动力学数学建模中,旋翼气动力建模的核心是如何建立二元翼型的气动力模型、旋翼尾迹模型和桨叶运动模型,三者相互作用、相互影响。旋翼气动力建模技术随着上述模型的发展而不断完善。

2.1.1 二元翼型的气动力模型

二元翼型的气动力模型可通过定常或非定常、线性或非线性的不同组合获得,选择何种组合与直升机的飞行状态有关。

即使直升机在定常飞行状态,旋翼桨叶剖面(翼型)一直在作周期性的俯仰和沉浮运动,其气动力具有非定常的特点。然而,桨叶剖面的非定常气动力计算并不是一件容易的事,即使采用精细化的计算流体力学(CFD)方法也难以得到直升机真实桨叶剖面的气动力。目前虽有很多方法,但结果却有较大差异[65-72]。对于飞行动力学建模而言,其研究的范畴大都属于低频响应,所以在很长一段时间内直升机飞行动力学数学建模中采用准定常线性模型计算二元翼型气动力。二元翼型的准定常非线性气动力模型通过大量的风洞静态试验得到不同迎角和不同马赫数下的二元翼型升力和阻力特性[22]。为了获得翼型的非线性特性,试验中翼型的迎角范围大大高于翼型的失速迎角,美国国家航空航天局(NASA)对一些常用翼型提供±180°迎角范围内的气动特性数据。马赫数的试验范围一般都在0～1.0的范围内进行,以研究不同马赫数对翼型气动特性的影响。实践证明,二元翼型的准定常线性模型对研究直升机定常飞行状态的平衡、操纵性和稳定性具有足够的精度,这也是直升机飞行动力学模型长期采用准定常线性模型的主要原因。但是对于作高速前飞和机动飞行的直升机来说,由于准定常线性模型无法考虑直升机重载大速度前飞和机动飞行时前行桨叶的压缩性和后行桨叶的动态失速特性,采用二元翼型准定常线性气动力模型与实际情况有较大的出入。准定常非线性气动力模型由于没有考虑二元翼型的动态失速而引起的升力动态过量会低估旋翼的载荷[73-74]。

为了弥补二元翼型准定常非线性气动力模型的不足,Leishman和Beddoes建立了翼型非定常/动态失速气动模型[75]。该模型将翼型气动力的计算分为附着流气动力、后缘分离气动力和动态失速(前缘分离)气动力三部分。在附着流状态,采用指数响应方法来计算翼型任意运动下的气动力。通过前缘压力来判断翼型是否产生前缘分离,判断的依据是垂直力系数是否大于前缘气流分离的临界垂直力系数,该系数是马赫数的函数,其大小可以通过静态翼型试验测量来确定。

2.1.2 旋翼尾迹模型

旋翼气动力和力矩与旋翼尾迹有着非常密切的关系,在直升机飞行动力学的旋翼气动力建模发展过程中采用了多种旋翼尾迹模型[76],从最简单的桨盘处均匀诱导速度模型到自由尾迹模型,以及此后发展出的高分辨率尾迹模型。

均匀诱导速度模型处理的是桨盘上的诱导速度分布与桨盘气动载荷分布之间的关系,它是一种特殊的尾迹模型,由动量理论得到[77]。在前飞状态,旋翼尾迹向后倾斜,桨盘诱导速度分布的非均匀性增加,在桨盘纵向和横向都存在明显的梯度变化,动量理论不再适用。为此,Coleman等[78]建立了反映尾迹倾斜效应的线性诱导速度模型。该模型在中等到大速度前飞状态能够给出合理的诱导速度分布,但在低速飞行状态,由于尾迹畸变严重,其准确性受到影响。此外,由于未考虑诱导速度的动态特性,上述模型仅适用于稳定飞行状态。

Carpenter和Friedovich[79]对动量理论进行了扩展,考虑了旋翼受到扰动时气流产生的附加惯性效应,建立了能反映诱导速度动态变化的动态入流模型,并以一阶常微分方程的形式给出。Pitt-Peters和Peters-He基于加速度势理论,建立了Pitt-Peters动态入流模型[34]及其广义形式的Peters-He有限状态(高阶)入流模型[42]。但上述模型成立的条件是来流速度须远大于旋翼桨盘平面的诱导速度,因此动态入流模型及有限状态(高阶)入流模型仅适用于低载荷旋翼或中等到大速度前飞状态的旋翼。

上述入流模型一般仅能给出桨盘平面处的诱导速度分布,由于缺乏旋翼尾迹到达机身等直升机部件处的详细信息,因而不适合于旋翼尾迹对机身、尾翼等的气动干扰计算。

为了将动态入流模型推广到旋翼桨盘平面以外的位置且能反映旋翼尾迹的畸变,Barocela[80]、Krothapalli[81]、Zhao[82-83]、Rosen和Isser[84-85]以及Keller[86-87]等提出预定弯曲曲率的旋翼涡管尾迹模型,并在此基础上,定义了一个尾迹弯曲参数Kre,以反映旋翼桨盘诱导速度梯度与尾迹弯曲曲率之间的比例关系,通过合理选择Kre值,能有效提高对旋翼和机体运动预测的准确性,但是为了使计算结果与飞行试验结果吻合,在悬停状态Kre需要取2.0,而在中速前飞状态需要取1.0。Bhagwat[88]、徐进[89]的研究发现Kre的取值与前飞速度、旋翼角速率以及旋翼拉力大小密切相关。事实上,人为预定的旋翼涡管尾迹模型(便于解析推导)并不能充分体现旋翼尾迹结构的所有畸变形式。

相比于动态入流模型,自由尾迹模型允许涡元随当地气流速度运动,能自动计入尾迹自诱导和机体非定常运动引起的尾迹畸变,因此更适合于尾迹畸变严重的悬停、低速飞行的旋翼非定常气动力计算以及直升机气动干扰的计算。

自由尾迹模型基于旋翼涡流理论[90],早期的自由尾迹模型多采用显式Euler时间推进格式,但其数值稳定性欠佳,其实用性受到影响。针对数值不稳定问题,有两类解决方法:第1类方法是引入尾迹周期性边界条件对尾迹的更新过程进行约束,该方法后来发展成经典的松弛类自由尾迹方法。第2类方法是采用高阶时间推进格式的预测-校正方法改善计算过程中的数值振荡,该方法已发展成为时间准确旋翼自由尾迹方法,目前已用于直升机的动态响应和机动飞行计算。

基于线涡离散的自由尾迹模型是目前较为成熟、应用广泛的一种方法。线涡离散的自由尾迹方法在保证精度的同时可以获得很高的计算效率,但线涡方法基于势流假设,且无法计入黏性,为了提高计算效率,研究者凭经验设定桨尖涡的卷起位置以及涡核模型,对这些经验参数的依赖直接限制了自由尾迹方法的适用性。为了寻求更为合理的尾迹模型,Lee和Na[91-92]基于涡团法建立了一种新的旋翼尾迹方法,该旋翼尾迹方法呈现出良好的数值特性,然而受自诱导速度计算效率低下的影响,该模型并未得到进一步发展。

近年来,得益于快速多极子算法(FMM)的发展[93],很多学者开始将其引入到高分辨率的一般涡方法研究中,并在近几年逐步应用于旋翼涡尾迹方法的研究。Brown等[94-95]基于有限体积法首先建立了适用于高精度旋翼尾迹特性研究的涡输运方法(VTM),He和Zhao[96-97]建立了高分辨率旋翼尾迹的黏性涡粒子方法(VVPM)。这些方法不仅继承了无黏自由尾迹方法的优点,同时还能捕捉尾涡黏性耗散以及尾迹结构变化的作用。

但上述方法在处理桨叶时一般采用升力线或升力面模型,因而无法捕捉桨叶近体流域的细节流动特征,限制了模型的整体精度,直接制约了VTM和VVPM方法优势的发挥。基于Navier-Stokes方程的旋翼CFD方法能精确捕捉桨叶气流分离与失速以及激波等流动细节特征,但受其固存的数值耗散问题的困扰,引起涡量的非物理过快衰减。为此,一些学者开始尝试将尾迹方法与旋翼CFD方法相结合,发展高分辨率旋翼尾迹方法与CFD的混合方法[98-99],使旋翼尾迹方法和CFD方法两者的优缺点形成互补,充分发挥CFD方法捕捉桨叶近体流场细节特征的优势和旋翼尾迹方法捕捉尾迹黏性耗散以及拓扑结构变化的特点。

2.1.3 桨叶运动模型

桨叶运动包括挥舞、摆振及变距运动,直升机飞行动力学建模主要关注桨叶的挥舞运动,旋翼作为直升机的操纵面和推进器也是通过桨叶的挥舞运动来实现的。

当直升机作定常飞行时,各片桨叶空气动力的周期特性基本相同,各片桨叶的运动轨迹基本一致,桨尖保持在同一平面内,可用桨盘的锥度角、后倒角和侧倒角来描述旋翼桨叶的挥舞运动,即桨盘平面方法,据此确定旋翼的气动合力方向及与机体运动的相互影响[17-18]。这种方法具有物理概念清晰、易于数学表达等优点。

当直升机作过渡飞行和机动飞行时,作用在桨叶上的气动力和惯性力均处于较大幅度的变化之中,各片桨叶的运动轨迹不尽相同,此时没有稳定的桨盘平面。若仍采用桨盘平面方法来描述挥舞运动并确定旋翼的气动力,则与实际情况有很大出入。目前有两种处理方法,一种是仍然假设各片桨叶具有相同的轨迹,但考虑其动态变化,即[17-18]

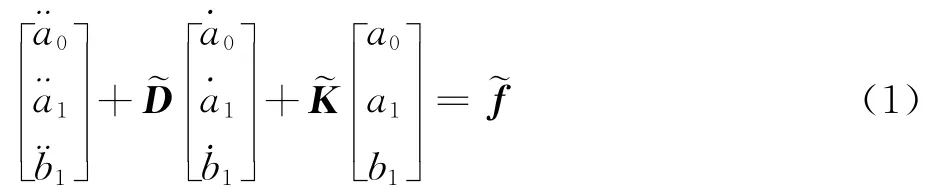
式中:a0、a1和b1分别为旋翼的锥度角、后倒角和侧倒角;~D、~K分别为桨叶挥舞运动的阻尼和刚度矩阵;~f为外激励。显然式(1)仅仅考虑了桨盘平面的动态变化,适用于小幅度的操纵响应。另一种方法是完全抛弃各片桨叶的桨尖保持在同一平面内的假设,在旋转坐标系下分别研究每片桨叶在旋转过程中的挥舞运动[22],能充分反映直升机作非定常飞行时机体角运动引起的哥氏力以及机体角加速度和加速度引起的附加惯性力。通过坐标转换可将桨叶旋转轴系下的挥舞运动转换到非旋转轴系桨叶的挥舞运动。显然,这种方法也适用于直升机的定常飞行,此时,各片桨叶具有相同的轨迹,回归到桨盘平面的情况。

桨叶的挥舞运动与旋翼的桨毂形式直接相关,影响桨叶挥舞的固有频率。对于中心铰旋翼,桨叶一阶挥舞运动的频率与旋翼转速相同,为了提高旋翼的操纵功效,现代直升机采用带挥舞铰偏置的铰接式旋翼或无铰旋翼,此时的桨叶挥舞运动可简化成如图4所示的形式[18],图中e为挥舞铰偏置量,Kβ为挥舞弹簧刚度,β为挥舞角。

图4简化方法适用于桨叶挥舞频率小于1.1Ω的桨毂,Ω为旋翼转速。对于X-2高速直升机,由于采用刚性旋翼,挥舞频率达到1.4Ω甚至更高,其一阶挥舞模态仍可以等效为一个含有弹簧约束的铰接式旋翼[2],为保证准确性,在等效时需满足两个方面的要求:首先确保刚性桨叶在等效后的挥舞频率与原挥舞频率相同;其次要让等效后的桨叶挥舞运动振型与原挥舞运动振型尽可能接近[68]。为了满足上述条件,可以采用如图5所示的等效桨叶刚性挥舞运动模型[71]。

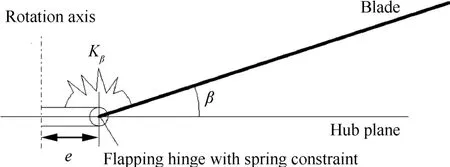
图4 铰接式或无铰旋翼的等效[18]Fig.4 Equivalent articulated or hingeless rotor[18]

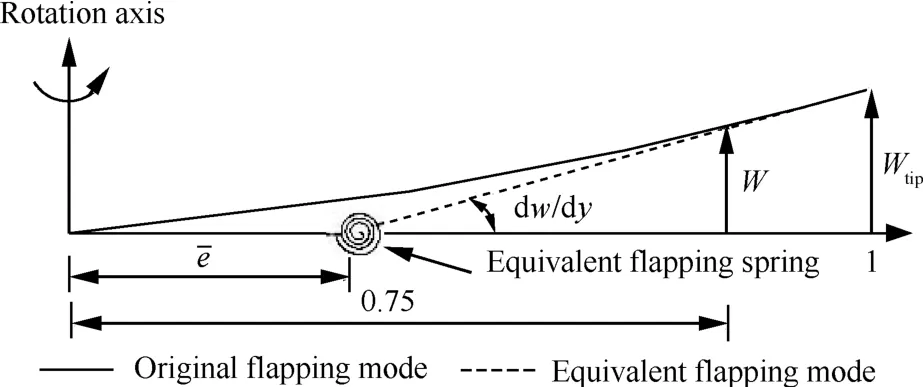
图5 刚性桨叶挥舞等效方法[71]Fig.5 Equivalent method for rigid blade flapping[71]

为了保证等效后的挥舞运动振型与原振型相似,无量纲等效挥舞铰外伸量¯e可表示为[71]式中:Wtip为原桨叶桨尖处的挥舞幅值;R为旋翼半径;W′0.75为原桨叶0.75(无量纲)处所对应的挥舞角。

为保证等效后挥舞频率不变,在等效挥舞铰处增加挥舞约束弹簧,其刚度可表示为[71]

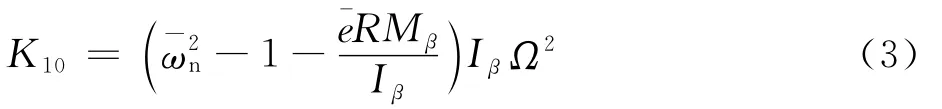
以上方法都是假定桨叶在挥舞运动过程中为刚性,是当前直升机飞行动力学建模的主流,随着直升机技术的不断发展,对直升机的速度和机动性提出了更高的要求,尤其对共轴刚性旋翼的高速直升机而言,将能够反映桨叶弹性变形的挥舞、摆振和变距运动耦合的弹性桨叶运动模型用于直升机飞行动力学模型对提高模型的置信度有重要作用。Du Val、He以及Turnour和Celi[39-40,44]建立了包含弹性桨叶的直升机飞行动力学模型,指出弹性桨叶运动与动态入流可有效改善对直升机异轴响应的预测精度。文献[100-101]建立了基于有限元分析的弹性桨叶模型,并与旋翼非定常自由尾迹模型和翼型非定常/动态失速模型集成,提高了悬停、低速飞行以及机动飞行状态旋翼载荷预测的准确性。建立弹性桨叶的运动模型并集成到直升机飞行动力学模型中是今后直升机飞行动力学数学建模的发展趋势。

2.2 旋翼/机身/尾桨/尾面气动干扰模型

在直升机飞行动力学建模过程中遇到的棘手问题之一是旋翼、机身、平尾、垂尾和尾桨之间存在的气动干扰问题。旋翼尾迹对机身和尾面的冲击改变其表面的流场和压力分布,引起机身和尾面上气动力和力矩的变化,影响直升机的平衡;而机身造成的气流阻塞引起旋翼、尾桨的尾流变化,导致旋翼、尾桨空气动力的变化。

直升机各部件之间的气动干扰问题一直是直升机界面临的一个广泛而棘手的难题。图6为直升机由悬停转入前飞时旋翼对平尾的气动干扰示意图,当直升机由悬停转入前飞时,旋翼尾迹向后偏斜,冲击到平尾产生抬头力矩,随着前飞速度的增加,旋翼尾迹上抬离开平尾,此时平尾产生低头力矩,影响直升机的配平操纵,并可能诱发直升机的动不稳定,使操纵响应的轴间耦合复杂化,严重损害直升机的操纵品质。在UH-60黑鹰直升机的研制过程中,其竞争机型YUH-61直升机因旋翼、机身间距太小引起旋翼机身气动干扰而导致严重振动,如图7所示。AH-64阿帕奇直升机在研制过程中都曾多次更改平尾的布局方式,但仍无法满足飞行品质规范的要求,最后不得不采用复杂的联动平尾方案以解决这一干扰问题,如图8所示。

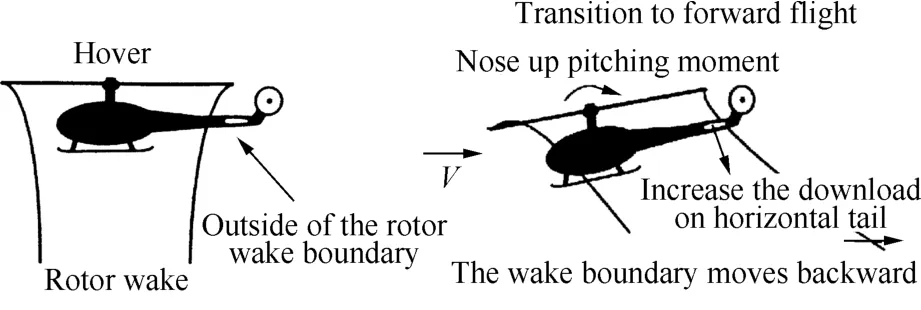
图6 旋翼尾迹对平尾的气动干扰Fig.6 Aerodynamic interference of rotor wake with horizontal tail

图7 YUH-61与UH-60旋翼、机身间距对比Fig.7 Comparison of rotor and fuselage spacing of YUH-61 and of UH-60

图8 AH-64直升机定型前后的平尾布局Fig.8 Layout of horizontal tail before and after the setting of AH-64

20世纪70年代,YUH-61A直升机旋翼/机身严重的气动干扰问题引起了美国直升机界对气动干扰问题的高度重视。波音直升机公司启动了持续7年之久的UTTAS计划,通过大量而全面的试验,研究者揭示了许多由气动布局引起的部件间气动干扰的机理,积累了大量的试验数据,推动了气动干扰问题的深入研究。

旋翼对直升机其他部件的下洗或侧洗效应主要影响这些部件的当地动压、迎角和侧滑角。由于旋翼尾迹随时间和空间都在发生变化,用理论分析方法来计算这些影响是一项非常艰巨的工作,一般通过风洞试验来确定。图9是某直升机平尾处动压[7],图中ˉqv为动压比(平尾当地动压与自由来流动压之差与自由来流动压的比值),vh为悬停诱导速度,从图中可以看出,某型直升机的平尾在一定的前飞速度范围内受旋翼等部件的干扰,当地动压高于自由来流动压。

旋翼尾迹在机身等部件上引起的下洗或侧洗可以表示为[8]式中:vi为旋翼桨盘处的诱导速度;k为旋翼对机身等部件的下洗或侧洗因子,它是旋翼尾迹角(定义悬停时的旋翼尾迹角为0°,大速度前飞时接近90°)及旋翼/机身相对位置的函数,不同的部件对应不同的k值。

图10给出了下洗因子k与旋翼尾迹倾斜角Χ的关系[8],从图中可以看出,当尾迹倾斜角在0附近时下洗因子近似为0,表示大速度前飞时,可以不考虑旋翼尾迹的影响。当旋翼尾迹倾斜角为90°时,下洗因子为2,即在悬停状态,旋翼在机身处的下洗速度为旋翼桨盘处的2倍,这与动量理论的结论一致。

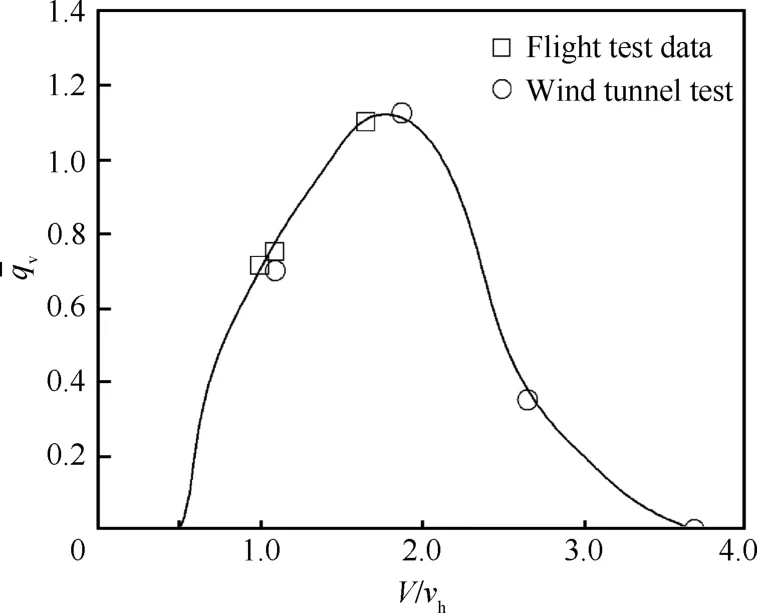
图9 某型直升机平尾动压[7]Fig.9 Aerodynamic pressure at horizontal tail[7]

图10 旋翼下洗因子与尾迹角的关系[8]Fig.10 Relationship between rotor downwash factor and wake angle[8]

上述方法仅仅提供了旋翼在机身、平尾、垂尾和尾桨上引起下洗速度的处理原则,在具体建模时,应根据直升机飞行状态和直升机各部件的气动布局确定哪些部件受旋翼尾迹的影响,哪些部件不受旋翼尾迹的影响。在研究直升机的过渡飞行和机动飞行时,还应考虑飞行过程中某一部件在旋翼尾迹区内和尾迹区外的动态变化情况,这些都给数学建模造成了困难。

20世纪80至90年代,随着旋翼自由尾迹研究的不断深入,人们开始从理论上研究直升机气动干扰问题,通过建立有效的旋翼机身气动干扰的理论预测模型[102-109],以期能够确定由气动干扰引起的在旋翼和机身上的非定常气动载荷。

为验证理论预测模型的正确性,美国佐治亚理工学院[110-114]和马里兰大学[115-117]在1989—1991年期间分别利用简单的几何旋成体作为机身建立了旋翼/机身组合模型,进行了大量的旋翼机身气动干扰风洞试验研究,测量了各种不同状态下旋翼/机身的干扰速度场和机身表面压力分布,这些试验结果成为了后人理论分析方法验证的基准。

随着基于无黏涡丝法的非定常旋翼自由尾迹方法的数值稳定性问题取得突破[118],气动干扰理论模型用于直升机飞行动力学建模,Horn[52]和Ribera[53]等将时间精确自由尾迹分析方法与已有直升机飞行动力学模型集成,美国CDI公司的Wachspress等[119]则将时间精确自由尾迹分析方法移植到著名的CHARM[53]直升机动力学综合分析软件,并通过与倾转旋翼机直升机模式模型试验结果[117]的对比表明自由尾迹模型能提高直升机气动特性预测的准确性。欧洲阿古斯塔直升机公司的D'Andrea[54]采用时间精确自由尾迹分析方法和非结构化面元网格技术发展了用于直升机气动干扰分析的ADPANEL方法,并成功用于倾转旋翼机的直升机飞行模式和固定翼飞机飞行模式的分析[120]。由于旋翼自由尾迹方法允许尾迹以当地气流速度自由运动,不仅能自动捕捉尾迹自诱导畸变,同时也能准确反映旋翼角运动诱导的尾迹结构畸变,因此更符合实际情况。采用前面所述的高分辨率旋翼尾迹方法建立直升机的气动干扰分析方法并集成到直升机飞行动力学模型中是今后直升机飞行动力学数学建模的发展趋势。

2.3 发动机/燃油调节系统的建模

直升机旋翼由发动机驱动,旋翼系统和发动机系统之间存在着复杂的交联耦合[121]。对作定常飞行的直升机来说,直升机的飞行状态和旋翼的工作状态相对稳定,直升机的需用功率变化不大,即发动机的负载几乎是恒定的,此时发动机的动态特性对直升机飞行特性的影响不大。但在过渡飞行和机动飞行状态,驾驶员需要不断地对直升机进行操纵,除了直升机的飞行状态发生变化、旋翼的需用功率也会不断变化,要求发动机的工作状态随之发生变化,满足旋翼需用功率不断变化的要求,如果此时忽略发动机的动态特性,其结果是不合理的[122]。为了满足上述要求,需要对旋翼、发动机以及它们之间的耦合进行建模,以考虑发动机机动特性对直升机飞行特性的影响[123]。图11给出了直升机旋翼、发动机之间的耦合逻辑关系[124]。

发动机动力学特性的研究长期独立于直升机飞行动力学的研究之外,对发动机研究者而言,认为发动机的负载(直升机的需用扭矩)是恒定的,忽视直升机旋翼的动力学特性对发动机的影响。例如,Ballin根据气动热力学定律,建立了T-700涡轴发动机部件级实时仿真模型[125]。之后Ahmet等在上述实时仿真模型的基础上,采用分段辨识的方法,建立了T-700涡轴发动机的简化线性模型[126]。同样,直升机飞行动力学的研究也忽视发动机系统对其飞行特性的影响,认为发动机能随时满足直升机对功率的需求。例如,Chen于20世纪70年代末建立的ARMCOP模型仅适用于旋翼系统的设计与分析,并没有包含发动机动态特性模型[127]。

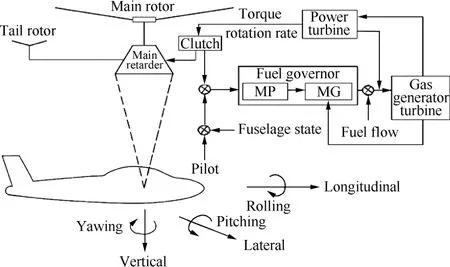
图11 直升机旋翼、发动机耦合关系[124]Fig.11 Coupling between helicopter rotor and engine[124]

Peter等提出了用于直升机飞行动力学研究的发动机/燃油调节系统的简单模型,该模型将压气机、油门控制、燃气涡轮、动力涡轮及燃油调节器等发动机部件的动力学特性用一个二阶环节来代替,虽然结构简单,使用方便,但二阶环节忽略了与发动机有关的许多细节问题,直接影响旋翼与发动机之间的耦合作用[128]。Sikorsky公司的GENHEL模型首次对T-700发动机及燃油调节控制进行建模,形成了包含发动机动力学特性的直升机旋翼/发动机一体化模型。但是,GENHEL模型中的发动机模型并不是全状态变量模型,它忽略了发动机燃气涡轮进口压力和动力涡轮进口压力对发动机动态特性的影响,仍是简化的发动机模型[129-130]。尽管如此,该模型仍是当前直升机飞行动力学最合适的发动机/燃油调节系统模型。

2.4 复杂非线性系统的集成与求解

直升机由多个系统组成,这些系统的动力学特性各不相同,且存在各种非线性因素,因此,直升机飞行动力学模型是由多个非线性子系统组成的复杂动力学系统。目前复杂非线性系统的求解方法尚不健全,如何求解复杂动力学非线性系统是直升机飞行动力学数学建模过程中必须事先考虑的。

第一,直升机机体运动是一个具有低频特性的动力学系统,且纵横向运动耦合很严重,因而,描述直升机机体运动的微分方程组是非线性的。旋翼、机身、平尾、垂尾和尾桨之间的气动干扰使非线性问题变得更加复杂,旋翼的下洗或侧洗使得机身、平尾、垂尾和尾桨的气动力变得不连续,给数学计算带来很多难题。

第二,旋翼尾迹模型本身在数值稳定性和收敛性以及计算效率方面还存在不足,悬停和低速飞行状态的计算结果并不令人满意。原因是描述直升机运动的非线性微分方程属于连续系统,而描述尾迹运动的差分方程是离散系统,两者相互嵌套,要求有一种成熟的、高效的和相互耦合的求解方法。Theodore[131]和Ribera[53]为了将Bagai[132]和Bhagwat[88]的自由尾迹模型集成到FLEXUM模型中以及Spoldi[50]和Horn[52]等为了将CDI公司的CHARM自由尾迹模型集成到GENHEL模型中,只能采用简化的自由尾迹模型,并采用松耦合的形式处理尾迹模型和旋翼动力学模型的耦合关系,以提高整个飞行动力学模型的求解效率。当然,上述研究对尾迹模型和已有的飞行动力学模型在集成方法、耦合求解以及实时仿真等方面做了一定的研究,并初步指出了旋翼自由尾迹模型对于提高直升机飞行动力学模型置信度的潜力。

第三,翼型气动力非定常和动态失速特性影响旋翼桨叶的气动载荷,虽然Leishman-Beddoes模型[75]、ONERA模型[73-74]以及Johnson模型[3]等在桨叶载荷计算、旋翼气弹分析等领域已经得到了广泛的应用,但桨叶非定常气动特性着重考虑尾迹中脱体涡的影响,当旋翼尾迹模型与翼型非定常气动力模型用于直升机飞行动力学建模时,应避免重复计入旋翼脱体涡引起的非定常效应。

第四,对于桨叶动力学模型,桨叶各自由度之间以及桨叶与机体之间的惯性耦合使得旋翼/机身耦合的动力学方程通常表示成隐式常微分方程的形式,与传统的飞行动力学模型以显式微分方程表示的形式完全不同,需要寻求新的数值求解方法。Turnour和Celi[44]通过解析推导的方式将旋翼/机体耦合动力学方程中与加速度有关的惯性耦合项分离出来,重新表示成标准的一阶常微分方程。这种方法虽然过程非常复杂,容易出错,但具有通用性。

第五,发动机/燃油调节系统的引入是为了使直升机飞行动力学模型适合于直升机机动飞行的研究。与定常飞行相比,机动飞行状态下的直升机飞行动力学模型的非线性程度进一步恶化,同时使得发动机/燃油调节系统的非线性因素更加严重,这种强非线性系统的相互耦合给系统的求解工作带来了许多困难。

可以预见,随着旋翼气动力模型、直升机气动干扰模型的复杂程度不断提高,直升机飞行动力学模型的集成及其相应的求解难度不断增加,如何在直升机飞行动力学模型的复杂度和求解效率上进行综合与集成是当前乃至未来高置信度直升机飞行动力学数学模型需要解决的问题。

2.5 机动飞行逆解

直至今天,直升机机动飞行研究的主要手段仍然是逆解方法,虽然逆解方法本身仍在不断完善发展[133-142],但是,逆解方法有两个方面有待完善。第一,由于逆解方法是通过预先设定的飞行轨迹,用优化方法来确定完成机动科目所需的座舱操纵,为此需事先对某一机动科目的轨迹给出数学表达式,由于飞行品质规范ADS-33E-PRF[1]所定义的23种机动科目,有相当一部分科目没有固定的飞行轨迹,无法对其轨迹进行数学描述,需寻求一种通用的机动科目描述方法。第二,逆解方法通过反求直升机飞行动力学方程组来获得实现某一机动科目的操纵量,在数学上是根据输出求输入,解不唯一,故需通过约束优化方法进行反复迭代,得到约束条件下的一种最优解,因此,逆解方法的计算效率比较低。

针对逆解方法面临的问题,文献[143]提出了一种直升机机动飞行科目的逆解新方法,该方法综合运用直升机飞行动力学模型、飞行控制以及导航策略,确定实现机动飞行科目所需的座舱操纵。其中,机动飞行科目用若干导航参数进行数学描述,与轨迹描述相比,机动科目的数学表达方式更简单通用,可以实现ADS-33E-PRF中定义的所有机动科目的描述。完成机动飞行科目所需的操纵通过直升机飞行动力学模型与飞行控制来确定,该过程只需要按照规范对机动科目的性能要求对飞行动力学模型进行一次求解就可以得到所需的操纵量,不需要反复迭代优化,所以计算效率得到显著提升。

直升机机动飞行的逆解方法能获得满足飞行品质规范规定的性能指标要求所需的操纵,但得到的操纵只是实现该机动飞行科目众多操纵方法之一,能否被驾驶员接受,是否满足驾驶员的评定等级要求尚未涉及,是有待进一步研究的内容。

3 结 论

直升机飞行动力学数学建模发展至今已取得了很大的进步,但直升机飞行力学的发展以及现代直升机对飞行性能和飞行品质的要求是一个需要长期、深入研究的课题,从目前的技术现状而言,直升机飞行动力学数学建模的发展趋势可总结如下:

1)提升旋翼气动力模型的置信度仍是直升机飞行动力学建模的关键。经过多年的发展,旋翼流场由最初的滑流模型发展到高分辨率旋翼尾迹模型,但高分辨率旋翼尾迹模型在处理桨叶时一般采用升力线或升力面模型,尚未涉及桨叶近体流域的细节流动特征,限制了旋翼气动力模型的整体精度。当前的旋翼气动力模型能有效预测前进比≤0.35的气动力,但对于前进比＞0.35的旋翼,由于对翼型动态失速以及反流区的流动细节认识尚未完全掌握,旋翼气动力模型的正确性有待提高。

2)现有的分析方法对直升机气动干扰的正确预测还相当有限,不仅与旋翼尾迹的分析精度有关,还需对直升机各部件之间气动干扰的特殊性进行有效处理,尽管有不少直升机气动干扰的分析方法,但尚需开展进一步的研究工作,在确保分析计算精度的前提下提高计算效率。

3)对直升机飞行动力学模型的复杂度和求解效率进行综合与集成是当前乃至未来高置信度直升机飞行动力学数学模型需要解决的问题。如何协调机体运动、旋翼旋转运动、旋翼尾迹运动及其相互耦合效应,并将这些运动和耦合效应引起的飞行器各部件非定常气动载荷、惯性载荷集成,其中描述机体运动、旋翼运动的非线性微分方程以及描述旋翼尾迹的运动方程相互嵌套,既要解决上述系统之间的信息交换,还需解决时间推进上的协调机制,是直升机飞行动力学模型集成及其数值求解方法面临的关键问题。

4)直升机机动飞行的逆解方法能获得满足飞行品质规范规定的性能指标要求所需的操纵。由于逆解方法是根据动力学系统的输出求输入,逆解得到的操纵只是实现该机动飞行科目众多操纵方法之一,能否被驾驶员接受,是否满足驾驶员的评定等级要求有待进一步研究。

5)近年来,新构型旋翼飞行器不断出现,飞行动力学建模面临新的问题,如倾转旋翼机旋翼动态倾转过程中的旋翼尾迹畸变及对机翼的干扰、共轴刚性旋翼复合式高速直升机的桨叶动力学特性与常规直升机桨叶动力学特性的显著不同以及由此引起的操纵问题。可以预见,随着直升机技术的不断发展,今后还会有其他的新型旋翼飞行器问世。如何针对新构型旋翼飞行器的构型特点建立高置信度的飞行动力学数学模型,是直升机飞行动力学数学建模应关注的新问题。

[1] BASKETT B J.Aeronautical design,performance specification,handing qualities requirements for military rotorcraft:ADS-33E-PRF[S].Alabama:AMCOM,2000.

[2] 高正,陈仁良.直升机飞行动力学[M].北京:科学出版社,2003:24-42.GAO Z,CHEN R L.Helicopter dynamics[M].Beijing:Science Press,2003:24-42(in Chinese).

[3] JOHNSON W.Helicopter theory[M].New Jersey:Princeton University Press,1980:23-902.

[4] SHERIDAN P F,SMITH R F.Interactional aerodynamics-a new challenge to helicopter technology[J].Journal of the American Helicopter Society,1980,25(1):3-21.

[5] PADFIELD G D.Helicopter flight dynamics:The theory and application of flying qualities and simulation modelling[M].2nd ed.Oxford:Blackwell Science Ltd,1996:23-500.

[6] PROUTY R W.直升机性能及稳定性和操纵性[M].高正,陈文轩,译.北京:航空工业出版社,1998:24-27.PROUTY R W.Helicopter performance stability and control[M].GAO Z,CHEN W X,translated.Beijing:Aviation Industry Press,1998:24-27(in Chinese).

[7] BLAKE B B,ALANSKY I B.Stability and control of the YUH-61A[J].Journal of the American Helicopter Society,1977,22(1):2-10.

[8] KISIELOWSKI E,PERLMUTTER A A,TANG J.Sta-bility and control handbook for helicopters:DCR-186[R].Pennsylvania:Dynasciences Corp Blue Bell Pa,1967.

[9] 佚名.军用直升机飞行品质规范背景材料和使用说明[M].北京:航空工业出版社,1986:15-128.YI M.Military helicopter flight quality specification background materials and instructions[M].Beijing:Aviation Industrry Press,1986:15-128(in Chinese).

[10] DOWELL E H,TANG D.Nonlinear aeroelasticity and unsteady aerodynamics[J].AIAA Journal,2002,40(9):1697-1707.

[11] STURISKY S H,LEWIS W D,SCHRAGE D P.Development and validation of a comprehensive real time AH-64 apache simulation model[C]//Proceedings of the 48th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1992:1267-1280.

[12] ANDERSON W D.Rexor rotorcraft simulation model[M].Florida:Eustis Directorate,1976:22-54.

[13] JOHNSON W A.Comprehensive analytical model of rotorcraft aerodynamics and dynamics:NASA-TM-81182/81183/81184[R].Washington,D.C.:NASA,1980.

[14] HILBERT K B.A mathematical model of UH-60 helicopter:NASA-TM-85890[R].Washington,D.C.:NASA,1984.

[15] PHILIPS J D.A mathematical model of SH-3G helicopter:NASA-TM-84316[R].Washington,D.C.:NASA,1980.

[16] HACKETT W E,GERNETT T S,BOREK B V.Mathematical model for the CH-47B helicopter capable of real time simulation of the full flight envelope:NASA-CR-166458[R].Washington,D.C.:NASA,1983.

[17] CHEN R T N.A simplified rotor system mathematical model for piloted flight dynamics simulation:NASA-TM-78575[R].Washington,D.C.:NASA,1979.

[18] CHEN R T N.Effects of primary rotor parameters on flapping dynamics:NASA-TP-1431[R].Washington,D.C.:NASA,1980.

[19] JOHNSON W A.Comprehensive analytical model of rotorcraft aerodynamics and dynamics.Part 1:Analysis s development:AD-A0900513[R].Washington,D.C.:AD,1980.

[20] TALBOT P D,TINLING B E,DECKER W A,et al.A mathematical model of a single main rotor helicopter for piloted simulation:NASA-TM-84281[R].Washington,D.C.:NASA,1982.

[21] SHERIDAN P F,ROBINSON C,SHAW J DR.Mathematical modeling for helicopter simulation of low speed,low altitude and steeply descending flight:NASA-CR-199385[R].Washington,D.C.:NASA,1982.

[22] HOWLETT J J.UH-60A black hawk engineering simulation program:NASA-CR-166309[R].Washington,D.C.:NASA,1981.

[23] BALLIN M G.Validation of a real-time engineering simulation of the UH-60A helicopter:NASA-TM-88360[R].Washington,D.C.:NASA,1987.

[24] SARATHY S,MURTHY U R.An advanced rotorcraft flight simulation model:parallel implementation and performance analysis:AIAA-1993-3550[R].Reston:AIAA,1993.

[25] KIM F D,CELI R,TISHLER N B.High order state space simulation models of helicopter flight mechanics[J].Journal of the American Helicopter Society,1993,38(4):16-27.

[26] LEWIS M S,AIKEN E W.Piloted simulation of one-onone helicopter air combat at NOE flight levels:NASATM-866686[R].Washington,D.C.:NASA,1985.

[27] HEFFLEY R K.Minimum-complexity helicopter simulation mathematical model:NASA-CR-177476[R].Washington,D.C.:NASA,1988.

[28] TALBOT P D,CORLISS L D.A mathematical force and moment model of a UH-1H helicopter for flight dynamic simulation:NASA-TM-73254[R].Washington,D.C.:NASA,1977.

[29] HE C J,LEWIS W D.A parametric study of real time mathematical modeling incorporating dynamic wake and elastic blades[C]//The 48th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1992:1181-1196.

[30] DAVIS J M.Rotorcraft simulation with aeroelastic rotor and improved aerodynamics representation:USAAMRDLTR-74-10[R].Maryland:ARL,1974.

[31] CHEN R T N,LEBACQZ J V,AIKEN E W.Helicopter mathematical models and control law development for handling qualities:NASA-CR-249[R].Washington,D.C.:NASA,1988.

[32] MILLER D G,WHITE F.A treatment of the impact of rotor-fuselage coupling on helicopter handling qualities[C]//Proceedings of the 43rd Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1987:631-644.

[33] PITT D M,PETER D A.Theoretical prediction of dynamic inflow derivatives[J].Vertica,1981,5(1):21-34.

[34] ZHAO X,CURTISS H C.A linearized model of helicopter dynamics including correlation with flight test[C]//Proceedings of the Second International Conference on Rotorcraft Basic Research.Maryland:College Park,1988:51-83.

[35] TAKAHASHI M D.A flight dynamic helicopter mathematical model with a single flap-lag-torsion main rotor:NASA-TM-102267[R].Washington,D.C.:NASA,1990.

[36] BALLIN M G.Validation of a real-time engineering simulation of the UH-60A helicopter:NASA-TM-88360[R].Washington,D.C.:NASA,1987.

[37] VON G W.Dynamic inflow modeling for helicopter rotors and its influence on the prediction of Cross-coupling[C]//Proceedings of the American Helicopter Society Aeromechanics Specialist Conference.Fairfax Virginia:AHS,1995:21-31.

[38] CHAIMOVITCH M,ROSEN A,RAND O,et al.Investigation of the flight mechanics simulation of a hovering helicopter[C]//Proceedings of the 48th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1992:1237-1256.

[39] DUVAL R.A real-time blade element helicopter simulation for handling qualities analysis[C]//Proceedings of the 15th European Rotorcraft Forum.Amsterdam:ERF,1989:766-785.

[40] HE C,DUVAL R.An unsteady airload model with dynamic stall for rotorcraft simulation[C]//Proceedings of the 50th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1994:931-948.

[41] HE C.Development and application of a generalized dynamic wake theory for lifting rotors[J].Building Service Engineering,1989,22(22):95-101.

[42] PETER D A,BOYD D,He C.Finite-state induced-flow model for rotors in hover and forward flight[J].Journal of the American Helicopter Society,1989,34(4):5-17.

[43] KIM F D,CELI R,TISCHLER M B.Forward flight trim calculation and frequency response validation of a high-order helicopter simulation model[J].Journal of Aircraft,1993,30(6):854-863.

[44] TURNOUR S R,CELI R.Modeling of flexible rotor blades for helicopter flight dynamics applications[J].Journal of the American Helicopter Society,1996,41(1):52-66.

[45] TURNOUR S R,CELI R.Effects of unsteady aerodynamics on the flight dynamics of an articulated rotor helicopter[J].Journal of Aircraft,1997,34(2):187-196.

[46] 杨超,洪冠新,宋寿峰.直升机飞行动力学放射非线性系统建模[J].北京航空航天大学学报,1997,23(4):471-476.YANG C,HONG G X,SONG S F.Affine nonlinear mathematical model for helicopter flight dynamics[J].Journal of Beijing University of Aeronautics and Astronautics,1997,23(4):471-476(in Chinese).

[47] 陈仁良.直升机飞行动力学数学建模及机动性研究[D].南京:南京航空航天大学,1998:25-56.CHEN R L.A mathematical model of helicopter flight dynamics and investigation of maneuverability[D].Nanjing:Nanjing University of Aeronautics and Astronautics,1998:25-56(in Chinese).

[48] 孙传伟.直升机飞行动力学模型与飞行品质评估[D].南京:南京航空航天大学,2001:20-66.SUN C W.Helicopter flight dynamics model and flight quality evaluation[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2001:20-66(in Chinese).

[49] 李建波,高正.直升机机动飞行仿真的气动建模及试验研究[J].航空学报,2003,24(2):116-118.LI J B,GAO Z.Aerodynamic modeling and experiment for simulation of helicopter maneuver flight[J].Acta Aeronautica et Astronautica Sinica,2003,24(2):116-118(in Chinese).

[50] SPOLDI S,RUCKEL P.High fidelity helicopter simulation using free wake,lifting line tail,and blade element tail rotor models[C]//Proceedings of the 59th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,2003:1880-1886.

[51] WACHSPRESS D A,QUACKENBUSH T R,BOSCHITSCH A H.First-principles free-vortex wake analysis for helicopters and tiltrotors[C]//Proceedings of the 59th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,2003:1763-1786.

[52] HORN J F,BRIDGES D O,WACHSPRESS D A,et al.Implementation of a free-vortex wake model in real-time simulation of rotorcraft[J].Journal of Aerospace Computing,Information,and Communication,2006,3(3):93-107.

[53] RIBERA M.Helicopter flight dynamics simulation with a time-accurate free-vortex wake model[D].Maryland:University of Maryland,2007:33-158.

[54] D'ANDREA A.Development of a multi-processor unstructured panel code coupled with CVC free wake model for advanced analysis of rotorcrafts and tiltrotors[C]//American Helicopter Society 64th Annual Forum.Fairfax Virginia:AHS,2008:120-139.

[55] 李攀.旋翼非定常自由尾迹模型及高置信度直升机飞行动力学建模研究[D].南京:南京航空航天大学,2010:20-99.LI P.Study on unsteady free wake model of rotor and high reliability helicopter flight dynamics modeling[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:20-99(in Chinese).

[56] RICHARD B,LEWIS W D.Huey cobra maneuvering investigations[C]//The 26th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1970:158-178.

[57] RODGER L,FINNESTEAD M W,WILLIAM J.C.Engineering flight test:AH-1G helicopter(Hueycobra)performance:AD-882220[R].Washington,D.C.:AD,1971.

[58] GEORGE M,DONALD Y.BROADHURST G,et al.Utility tactical transport aircraft system(UTTAS)maneuver criteria:AD-902707[R].Washington,D.C.:AD,1972.

[59] WOOD T L,LIVINGSTON C L.An energy method for prediction of helicopter maneuverability:AD-A021266[R].Washington,D.C.:AD,1971.

[60] WELLS C D,Wood T L.Maneuverability-theory and application[J].Journal of the American Helicopter Society,1973,18(1):10-22.

[61] WOOD T L,FORD D G,BRIGMM G H.Maneuver criteria evaluation program:AD-782207[R].Washington,D.C.:AD,1974.

[62] WOOD T L,WAAK T.Improved maneuver criteria evaluation program:AD-A080408[R].Washington,D.C.:AD,1979.

[63] THOMSON D G,BRADLEY R.An investigation of the stability of flight path constrained helicopter maneuvers by inverse simulation[C]//13th European Rotorcraft Forum.Arles.France:ERF,1987:121-141.

[64] 曹义华.直升机的机动飞行研究[D].南京:南京航空航天大学,1990:22-95.CAO Y H.Research on helicopter maneuver flight[D].Nanjing:Nanjing University of Aeronautics and Astronautics,1990:22-95(in Chinese).

[65] EVERSMAN W,TEWAI A.A reduced cost rationalfunction approximation for unsteady aerodynamics:AIAA-1990-1166[R].Reston:AIAA,2013.

[66] TYLER J C,LEISHMAN J G.Analysis of pitch and plunge effects on unsteady airfoil behavior[J].Journal of the American Helicopter Society,1992,37(3):68-82.

[67] YEN J G,YUCE M.Correlation of pitch-link loads in deep stall on bearingless rotors[J].Journal of the American Helicopter Society,1992,37(4):4-15.

[68] MELLO A F,RAND O.Unsteady frequency domain analysis of helicopter non-rotating lifting surfaces[J].Journal of the American Helicopter Society,1991,36(2):70-80.

[69] SHIN C,LOURENCO L,DOMMELEN L V.Unsteady flow past an airfoil pitching at a constant rate[J].AIAA Journal,1992,30(5):1153-1161.

[70] BEDDOES T S.A synthesis of unsteady aerodynamic effects including stall hysteresis[J].Vertica,1976,1(2):113-123.

[71] GRAY L.Wind tunnel test of thin airfoils oscillating near stall:USAAVLABS-TR68-89[R].Maryland:ARL,1968.

[72] AZUMA A,OBATA A.Induced flow variation of helicopter rotor operating in the vortex ring state[J].Journal of Aircraft,1968,5(4):381-386.

[73] TRAN C T,PITOT D.Semi-empirical model for the dynamic stall of airfoil of airfoils in view of the application to the calculation of the responses of a helicopter blade in forward flight[J].Vertica,1981,5(1):35-53.

[74] TRUONG V K.A 2-D dynamic stall model based on a half bifurcation[C]//Proceedings of the 19th European Rotorcraft Forum.Cernobbio:ERF,1993:23-23.

[75] LEISHMAN J G,BEDDOES T S.A generalized model for airfoil unsteady aerodynamic behaviour and dynamic stall using the indicial method[C]//Proceedings of 42nd Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1986:243-265.

[76] CHEN R T N.A survey of nonuniform inflow models for rotorcraft flight dynamics and control applications[J].Vertica,1990,14(2):147-184.

[77] LEISHMAN J G.Principles of helicopter aerodynamics[M].2nd ed.New York:Cambridge University Press,2006:78-198.

[78] COLEMAN R P,FEINGOLD A M,STEMPIN C W.Evaluation of the induced-velocity field of an idealized helicopter rotor:NACA-ARR-L5E10[R].Washington,D.C.:NACA,1945.

[79] CARPENTER P J,FRIEDOVICH B.Effect of a rapid blade-pitch increase on the thrust and induced-velocity response of a full-scale helicopter rotor:NACA-TN-3044[R].Washington,D.C.:NACA,1953.

[80] BAROCELA E B,PETER D A,KROTHAPALLI K R,et al.The effect of wake distortion on rotor inflow gradients and off-axis coupling:AIAA-1997-3579[R].Reston:AIAA,1997.

[81] KROTHAPALLI K R,PRASAD J V,PETER D A.Helicopter rotor dynamic inflow modeling for maneuvering flight[C]//Proceedings of the 55th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1999:498-509.

[82] ZHAO J,PRASAD J V,PETER D A.Investigation of wake curvature dynamics for helicopter maneuvering flight simulation[C]//Proceedings of the 59th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,2003:1887-1901.

[83] ZHAO J.Dynamic wake distortion model for helicopter maneuvering flight[D].Atlanta:Georgia Institute of Technology,2005:18-37.

[84] ROSEN A,ISSER A.A model of the unsteady aerodynamics of a hovering helicopter rotor that includes variations of the wake geometry[J].Journal of the American Helicopter Society,1995,40(3):6-16.

[85] ROSEN A,ISSER A.A new model of rotor dynamics during pith and roll of a hovering helicopter[J].Journal of the American Helicopter Society,1995,40(3):17-28.

[86] KELLER J D.An investigation of helicopter dynamic coupling using an analytical model[J].Journal of the American Helicopter Society,1996,41(4):322-330.

[87] KELLER J D,CURTISS H C.A critical examination of the methods to improve the off-axis response prediction of helicopters[C]//Proceedings of the 54th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1998:1134-1147.

[88] BHAGWAT M J.Mathematical modelling of the transient dynamics of helicopter rotor wakes using a time-accurate free-vortex methods[D].Maryland:University of Maryland,2001:22-97.

[89] 徐进.直升机大机动飞行中旋翼非定常空气动力研究[D].南京:南京航空航天大学,2007:25-95.XU J.Study on unsteady aerodynamic force of rotor in helicopter maneuvering flight[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007:25-95.

[90] CRIMI P.Theoretical prediction of the flow in the wake of a helicopter rotor:BB-1994-5-1[R].New York:Cornell Aeronautical Laboratory,1965.

[91] LEE D J,NA S U.Predictions of airloads and wake geometry for slowly starting rotor blades in hovering flight by using time marching free vortex blob method[C]//Annual Forum,52nd.Fairfax Virginia:AHS,1996:532-540.

[92] LEE D J,NA S U.Numerical simulations of wake structure generated by rotating blades using a time marching free vortex blob method[J].European Journal of Mechanics/B Fluids,1999,18(1):147-159.

[93] GREENGARD L,ROKHLIN V.A fast algorithm for particle simulations[J].Journal of Computational Physics,1987,73(2):325-348.

[94] BROWN R E.Rotor wake modeling for flight dynamic simulation of helicopters[J].AIAA Journal,2000,38(1):57-63.

[95] BROWN R E,LINE A J.Efficient high-resolution wake modeling using the vorticity transport equation[J].AIAA Journal,2005,43(7):1434-1443.

[96] HE C,ZHAO J.Modeling rotor wake dynamics with viscous vortex particle method[J].AIAA Journal,2009,47(4):902-915.

[97] ZHAO J,HE C.A viscous vortex particle model for rotor wake and interference analysis[J].Journal of the American Helicopter Society,2010,55(1):1-14.

[98] CAO Y H,YU Z Q,SU Y,Combined free wake/CFD methodology for predicting transonic rotor flow in hover[J].Chinese Journal of Aeronautics,2002,15(2):65-71.

[99] WHITEHOUSE G R,TADGHIGHI H,Investigation of hybrid grid-based computational fluid dynamics methods for rotorcraft flow analysis[J].Journal of the American Helicopter Society,2011,56(3):032004-1～032004-10.

[100]ZHAO J,HE C,Rotor blade structural loads analysis using coupled CSD/CFD/VVPM[C]//American Helicopter Society 69th Annual Forum.Fairfax Virginia:AHS,2013:40-62.

[101]LI P,CHEN R L.A mathematical model for helicopter comprehensive analysis[J].Chinese Journal of Aeronautics,2010,23(3):320-326.

[102]SMITH C A,BETZINA M D.Aerodynamic loads induced by a rotor on a body of revolution[J].Journal of American Helicopter Society,1986,31(1):29-36.

[103]LORBER P F,EGOLF T A.An unsteady helicopter rotor-fuselage aerodynamic interaction analysis[J].Journal of the American Helicopter Society,1990,35(3):32-42.

[104]CROUSE G L,LEISH MAN J G,BI N.Theoretical and experimental study of unsteady rotor/body aerodynamic interactions[J].Journal of the American Helicopter Society,1992,37(1):55-65.

[105]MAVRIS D N,KOMERATH N M,MCMAHON H M.Prediction of aerodynamic rotor-airframe interactions in forward flight[J].Journal of the American Helicopter Society,1989,34(4):37-46.

[106]KOMERATH N M,MAVRIS D M,LIOU S G.Prediction of unsteady pressure and velocity over a rotorcraft in forward flight[J].Journal of Aircraft,1991,28(8):509-516.

[107]QUACKENBUSH T R,LAM C M G,BLISS D B.Vortex methods for the computational analysis of rotor/body interaction[J].Journal of the American Helicopter Society,1994,39(4):14-24.

[108]AFFES H,XIAO Z,CONLISK A,et al.The three-dimensional boundary layer flow due to a rotor-tip vortex[C]//23rd Fluid Dynamics,Plasmadynamics,and Lasers Conference.Reston:AIAA,1993:3081-3081.

[109]BERRY J D,ALTHOFF S L.Inflow velocity perturbations due to fuselage effects in the presence of a fully interactive wake[C]//The 46th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1990:1111-1120.

[110]NORMAN T R,YAMAUCHI G K.Full-scale investigation of aerodynamic interactions between a rotor and a fuselage[C]//Proceedings of the 47th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1991:461-486.

[111]LIOU S G,KOMERATH N M,MCMAHON H M.Velocity measurement of airframe effects on a rotor in lowspeed forward flight[J].Journal of Aircraft,1989,26(4):340-348.

[112]LIOU S G,KOMERATH N M,MCMAHON H M.Measurement of the interaction between a rotor tip-vortex and a cylinder[J].AIAA Journal,1990,28(6):975-981.

[113]BRAND A G,MCMAHON H M,KOMERATH N M.Surface pressure measurements on a body subject to vortex wake interaction[J].AIAA Journal,1989,27(5):569-574.

[114]RAJAGOPALAN R G,MATHUR S R.Three dimensional analysis of a rotor in forward flight[J].Journal of the American Helicopter Society,1993,38(3):14-25.

[115]LEISHMAN J G,BI N.Measurement of a rotor flowfield and the effects on a fuselage in forward flight[J].Vertica,1990,14(3):401-415.

[116]LEISHMAN J G,BI N,SAMAK D K.Investigation of aerodynamic interactions between a rotor and a fuselage in forward flight[C]//The 45th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,1989:591-601.

[117]LEISHMAN J G,BI N.Investigation of rotor tip vortex interactions with a body[J].Journal of Aircraft,1993,30(6):879-888.

[118]BHAGWAT M J.Mathematical modelling of the transient dynamics of helicopter rotor wakes using a time-accurate free-vortex method[D].Maryland:University of Maryland,2001:22-95.

[119]WACHSPRESS D A,QUACKENBUSH T R,BOSCHITSCH A H.Rotorcraft interactional aerodynamics calculations with fast vortex/fast panel methods[C]//The 56th Annual Forum of the American Helicopter Society.Fairfax Virginia:AHS,2000:51-71.

[120]LIGHT J S.Results from an XV-15 rotor test in the national full-scale aerodynamics complex[C]//Annual Forum,53rd.Fairfax Virginia:AHS,1997:231-239.

[121]KENNETH W.Integrated flight-propulsion control specifications:accounting for two way coupling:AIAA-1994-3613[R].Reston:AIAA,1994.

[122]ROCK S M,NEIGHBORS K.Integrated flight/propulsion control for helicopters[J].Journal of the American Helicopter Society,1994,39(3):34-42.

[123]WARMBRODT W.Development of a helicopter rotorpropulsion system dynamics analysis:AIAA-1982-1087[R].Reston:AIAA,1982.

[124]BAILEY F J,Jr.A simplified theoretical method of determining the characteristics of a lifting rotor in forward flight:NACA Report 716[R].Washington,D.C.:NACA,1941.

[125]BALLIN M G.A high fidelity real-time simulation of a small turboshaft engine:NASA-TM-100991[R].Washington,D.C.:NASA,1988.

[126]AHMET D,ZHEN G,JONATHAN S L.A simplified dynamic model of the T700 turboshaft engine:NASA TM-105805[R].Washington,D.C.:NASA,1992.

[127]CHEN R T N.A simplified rotor system mathematical model for piloted flight dynamics simulation:NASA-TM-78575[R].Washington,D.C.:NASA,1979.

[128]PETER D T,BRUCE E,TINLING W,et al.A mathematical model of a single main rotor helicopter for piloted simulation:NASA TM-84281[R].Washington,D.C.:NASA,1982.

[129]THADDEUS T K.UH-60 black hawk engineering simulation model validation and proposed modifications:NASA CR-177360[R].Washington,D.C.:NASA,1987.

[130]KIM F D.Analysis of propulsion system dynamics in the validation of a high-order state space model of the UH-60:AIAA-1992-4150[R].Reston:AIAA,1992.

[131]THEODORE C R.Helicopter flight dynamics simulation with refined aerodynamic modeling[D].Maryland:University of Maryland,2000:22-99.

[132]BAGAI A.Contributions to the mathematical modeling of rotor flow-fields using a pseudo-implicit free-wake analysis[D].Maryland:University of Maryland,1995:20-88.

[133]THOMSON D G,BRADLEY R.An investigation of the stability of flight path constrained helicopter maneuvers by inverse simulation[C]//13th European Rotorcraft Forum.Arles:ERF,1987:122-142.

[134]HESS R A,GAO C,WANG S H.A generalized technique for inverse simulation applied to aircraft flight control[J].Journal of Guidance,Control and Dynamics,1991,14(5):920-926.

[135]曹义华,高正.直升机机动飞行的数学模拟[J].飞行力学,1990,3(1):22-32.CAO Y H,GAO Z.Mathematical simulation of helicopter maneuver flight[J].Flight Dynamics,1990,3(1):22-32(in Chinese).

[136]陈仁良,高正.直升机机动飞行的逆模拟[J].空气动力学学报,1999,17(3):339-345.CHEN R L,GAO Z.The inverse simulation of helicopter maneuver flight[J].Acta Aerodynamica Sinica,1999,17(3):339-345(in Chinese).

[137]THOMSON D G,BRADLEY R.The principles and practical application of helicopter inverse simulation[J].Simulation Theory and Practice,1998,6(1):47-70.

[138]THOMSON D G,BRADLEY R.Mathematical definition of helicopter maneuvers[J].Journal of the American Helicopter Society,1997,42(1-4):307-309.

[139]LEACOCK G R,THOMSON D G.Helicopter handling qualities studies using pilot modeling and inverse simulation[C]//American Helicopter Society 54th Annual Forum.Fairfax Virginia:AHS,1998:1325-1336.

[140]CELI R.Optimization-based inverse simulation of a helicopter slalom maneuver[J].Journal of Guidance,Control and Dynamics,2000,23(2):289-297.

[141]CAMERON N,THOMSON D G,SMITH D J.Pilot modeling and inverse simulation for initial handling qualities assessment[J].Aeronautical Journal,2003,107(1744):511-520.

[142]李建波,高正.基于逆仿真的直升机机动飞行科目数学模型及其应用[J].南京航空航天大学学报,2003,35(1):1-5.LI J B,GAO Z.Mathematical modeling and its application for helicopter maneuver flight based on inverse simulation[J].Journal of Nanjing University of Aeronautics&Astronautics,2003,35(1):1-5(in Chinese).

[143]吴伟.直升机飞行动力学模型辨识与机动飞行研究[D].南京:南京航空航天大学,2010:90-108.

WU W.Study on the identification of the flight dynamics model of helicopter and maneuvering flight[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:90-108(in Chinese).

A review of mathematical modeling of helicopter flight dynamics

CHEN Renliang*,Ll Pan,WU Wei,KONG Weihong

National Key Laboratory of Science and Technology on Rotorcraft Aeromechanics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

The mathematical model of helicopter flight dynamics is the basis for the design of the flight control system,and is also the tool for the design and assessment of helicopter flight quality.As the helicopter is a multi-body system,the mathematical modeling of helicopter flight dynamics should consider the coupling between motion,inertia,structure and aerodynamics,as well as the unsteady and nonlinear characteristics,so as to give the physical meaning and mathematical expression of each motion part.Therefore,the mathematical modeling of helicopter flight dynamics is a complicated process of analyzing and synthesizing different hypotheses and subsystem models.The paper reviews briefly the development of the flight dynamic modeling of the helicopter with a main rotor and a tail rotor.The emphasis is put on the modeling of main rotor aerodynamics,and aerodynamic interaction among the rotor,fuselage and tail rotor.lntegrated modeling of the main rotor and engine,as well as the research on maneuver flight,is also the focus of the paper.Suggestions for future research on helicopter flight dynamic modeling are also provided.

helicopter;rotor;flight dynamics;aerodynamic interaction;maneuvering flight

2016-11-07;Revised:2017-02-19;Accepted:2017-03-27;Published online:2017-04-19 11:24 URL:www.cnki.net/KCMS/detail/11.1929.V.20170419.1124.002.html

National Natural Science Foundation of China(11672128)

V212.4

A

1000-6893(2017)07-520915-17

10.7527/S1000-6893.2017.520915

2016-11-07;退修日期:2017-02-19;录用日期:2017-03-27;网络出版时间:2017-04-19 11:24

www.cnki.net/KCMS/detail/11.1929.V.20170419.1124.002.html

国家自然科学基金(11672128)

*通讯作者.E-mail:crlae@nuaa.edu.cn

陈仁良,李攀,吴伟,等.直升机飞行动力学数学建模问题[J].航空学报,2017,38(7):520915.CHEN R L,Ll P,WU W,et al.A review of mathematical modeling of helicopter flight dynamics[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):520915.

(责任编辑:鲍亚平)

*Corresponding author.E-mail:crlae@nuaa.edu.cn