高阶谐波控制对旋翼桨-涡干扰载荷和噪声的影响

王亮权,徐国华*,史勇杰,夏润泽

南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016

高阶谐波控制对旋翼桨-涡干扰载荷和噪声的影响

王亮权,徐国华*,史勇杰,夏润泽

南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016

直升机小速度平飞和斜下降飞行时会产生严重的桨-涡干扰(BVI)噪声。基于修正Beddoes尾迹/桨叶动力学耦合方法和Farassat 1A公式,建立了一个新的能够计入高阶谐波控制(HHC)影响的旋翼桨-涡干扰气动载荷和噪声计算模型。在该模型中,高阶谐波控制引起的桨尖涡附加位移通过对高阶入流进行时间积分推导得出,而单一阶次的谐波输入引起的各阶谐波响应通过传递函数来确定,传递函数则由桨叶的动力学特性计算。首先对HARTⅡ旋翼斜下降飞行状态的桨-涡干扰气动载荷进行了计算模拟,验证了所建立方法的可靠性。然后,着重研究了在典型的三阶谐波桨根激励下,不同输入相位对HARTⅡ旋翼桨-涡干扰气动载荷和噪声特性的影响。结果表明:桨叶的动力学特性尤其是扭转特性对高阶谐波控制效果影响显著,且高阶谐波输入的相位选择对桨-涡干扰噪声的控制至关重要,若控制相位选择不当,反而会增大旋翼噪声。

高阶谐波控制;直升机;旋翼;桨-涡干扰;气动载荷;噪声

直升机在小速度平飞和斜下降飞行时,桨叶尖部逸出的桨尖涡形成的尾迹停留在旋翼附近,使得桨尖涡很容易与后续的桨叶相互靠近甚至直接碰撞,产生所谓的桨-涡干扰(Blade-Vortex Interaction,BVI)现象[1]。由于桨尖涡的干扰,会使得桨叶诱导速度发生剧烈扰动,从而改变桨叶剖面上的迎角和气动载荷。在直升机飞行中,桨-涡干扰发生时桨叶与桨尖涡迅速靠近而后立即远离,在桨叶上形成频率很高的非定常载荷脉冲,这是桨-涡干扰噪声的声源。桨-涡干扰噪声不仅会严重增大军用直升机的声可探测性,也会限制民用直升机在城市的大规模使用。因此,研究旋翼桨-涡干扰噪声的抑制方法在理论和实际应用中都具有重要的价值。

国外对降低桨-涡干扰噪声已经开展了不少研究,Hardin和Lamkin[2]首先从理论上探讨了桨-涡干扰噪声的抑制方法,指出了桨尖涡强度、桨叶剖面上的升力、桨-涡干扰距离等参数对BVI强度的影响。随后,直升机界提出了多种控制BVI噪声的概念,包括高阶谐波控制(Higher Harmonic Control,HHC),单独桨叶控制(Individual Blade Control,IBC)和后缘小翼等[3]技术。高阶谐波控制和单独桨叶控制的机理相似,二者区别在于高阶谐波控制的激励器安装在旋翼自动倾斜器下方,各片桨叶桨根处受到的激励完全相同;单独桨叶控制的激励器则位于自动倾斜器上方,各片桨叶可分别施加激励。高阶谐波控制由于其控制律相对简单,成为了近年来的研究热点。

高阶谐波控制技术最早被国外学者用于直升机座舱振动水平抑制上,在 OH-6A、SA-349、S-76A等直升机上进行的飞行实测表明,H HC最高可以将座舱振动水平降低90%[4-6]。Giovanetti和Hall将HHC技术用于复合式直升机的性能优化,发现HHC能减小直升机高速前飞时的需用功率[7]。Splettstoesser等则在德国-荷兰DNW风洞中进行了BO-105直升机缩比模型的吹风试验[8],结果表明,HHC同样具有控制旋翼BVI噪声的潜力,适当的高阶谐波控制可以将BVI噪声降低4～6 d B。2009年,Boyd基于CFD/CSD耦合方法进行了HARTⅡ旋翼高阶谐波控制降噪模拟的尝试[9],为避免在捕捉桨尖涡时出现显著的非物理耗散,使用了总量高达6 900万的网格节点,以致消耗了大量的计算资源。国内有关HHC的研究较少,杨一栋和袁卫东对H HC的抑振效果进行了初步的仿真验证[10],冯剑波等利用自由尾迹方法进行了HHC主动控制研究[11],分析了不同控制相位下的BVI噪声抑制效果,但其研究是直接给桨距附加一个高阶谐波输入量,并未考虑由于桨根激励引起的桨叶真实弹性变形。

使用数值方法进行HHC对BVI噪声控制效果的模拟研究,是涉及到气动、动力学和噪声的多学科问题,其研究是富有挑战性的。由于HHC是在桨叶根部施加激励,通过桨叶的动力学响应来获得其控制效果,因而进行桨叶动力学建模是必要的。另一方面,为了有效地计算4～60倍桨叶通过频率的桨-涡干扰非定常载荷[12],需要所使用的气动模型具有良好的桨尖涡捕捉精度。2011年,Wall建立了一套所谓的修正Beddoes尾迹模型[13],该模型在性质上可归入预定尾迹类,具有解析表达式,能够像自由尾迹模型那样计入涡线的畸变和收缩,且不存在CFD所面临的数值耗散问题。修正Beddoes尾迹、自由尾迹、CFD 3种气动模型单步计算的耗时比约为1∶103∶106,修正Beddoes尾迹在计算效率方面具有突出优势,同时具有与自由尾迹相当的精度。Wall将该模型用于桨-涡干扰的研究,取得了良好的模拟结果[12]。

鉴于此,本文拟基于修正Beddoes尾迹/桨叶动力学耦合模型,并结合Farassat 1A公式,建立一套高效且能够计入高阶谐波控制输入影响的旋翼桨-涡干扰噪声模拟方法。与先前HHC侧重于减振研究不同的是,本文深入研究HHC对桨-涡干扰噪声特性的影响机理,并得到了如下结论:高阶谐波控制主要通过改变桨-涡垂直干扰距离影响桨-涡干扰噪声。

1 数值计算方法

为开展高阶谐波控制对旋翼桨-涡干扰气动载荷和噪声的影响研究,本文在修正Beddoes尾迹模型的基础上,推导建立了能够计入高阶谐波影响的气动模型,随后结合桨叶动力学模型确定各阶谐波之间的耦合效应,开发出一套适用于旋翼高阶谐波控制模拟的气动/动力学分析代码,并将其用于HHC状态下的噪声模拟。

1.1 基于修正Beddoes尾迹的旋翼气动模型

1.1.1 修正Beddoes尾迹模型

基于修正Beddoes尾迹模型确定旋翼尾迹形状,桨盘平面内的诱导入流分布为[14]

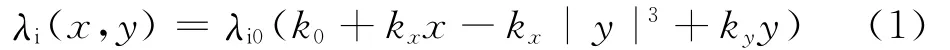
桨盘平面外的诱导入流分布为

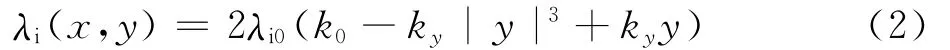
式中:

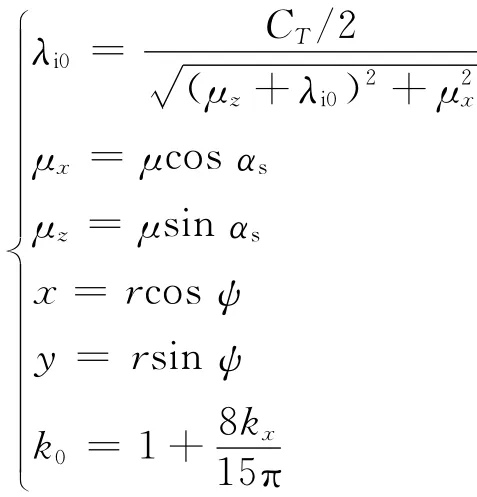
其中:CT为旋翼拉力系数;μ为前进比;αs为旋翼迎角;坐标系为右手系,坐标原点位于桨盘中心,x轴正方向沿着来流方向,y轴正方向指向90°桨叶方位角;kx和ky分别为旋翼纵向和横向入流分布系数;ψ为方向角。

对于从桨尖附近脱出的桨尖涡,以旋翼半径R为无量纲参数,令其坐标为(xv,yv,zv),有[15]

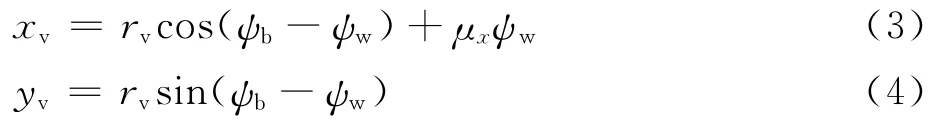
式中:ψb和ψw分别为桨叶所处方位角和桨尖涡涡龄角;rv为桨尖涡在桨叶上的逸出位置。

对式(1)和式(2)中的诱导速度场进行时间积分,并与旋翼轴向来流分量叠加,可得到桨尖涡的轴向位移为

式中:∫λidψ为诱导速度场引起的桨尖涡轴向位移。从桨盘前半区域(90°＜ψb＜270°)脱出的桨尖涡均会通过桨盘区域,而从桨盘后半区域(0°＜ψb＜90°和270°＜ψb＜360°)脱出则不会受到桨盘诱导速度场的影响,在进行积分计算时需要分别考虑。

图1为直升机小速度前飞时旋翼桨尖涡尾迹形状示意图,所计算的飞行状态对应的CT=0.003 3,μ=0.19,αs=-6.3°。从图中可以看出,此时桨尖涡的轴向(z方向)运动速度小,桨尖涡在运动4圈后仍然停留在桨盘附近,前行侧桨尖涡相对后行侧的卷起效应更明显。在桨盘平面内涡线与桨叶相交的位置,会发生强烈的桨-涡干扰,进一步带来严重的BVI噪声。

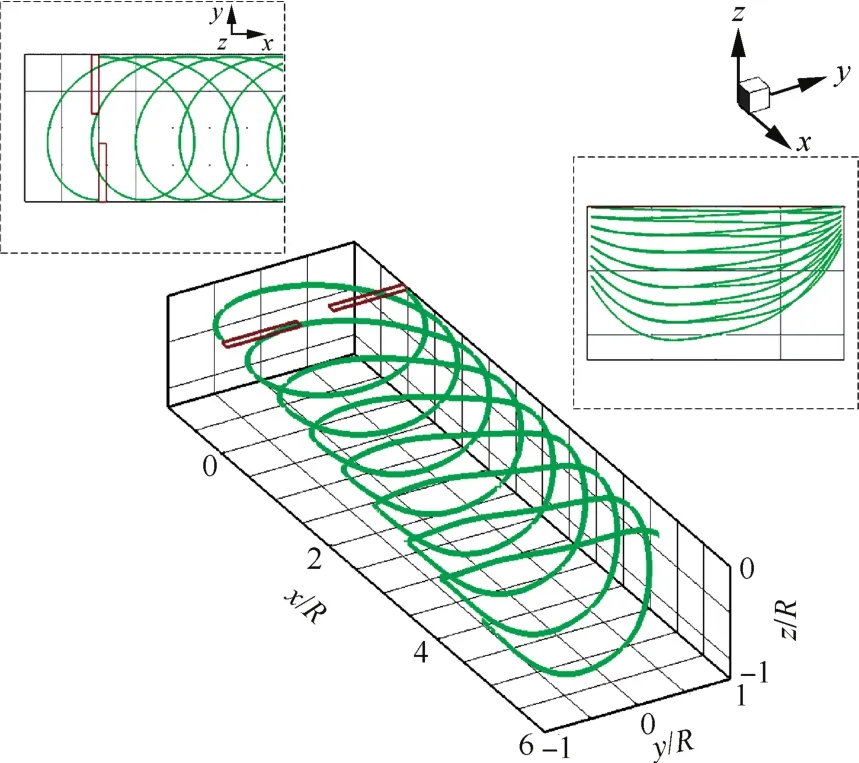
图1 修正Beddoes尾迹示意图Fig.1 Schematic of modified Beddoes wake

1.1.2 桨叶附着涡环量求解方法

将桨叶离散为N个单元,附着涡环量Γi位于桨叶1/4弦线处,而控制点位于3/4弦线。由尾随涡组成的旋翼近尾迹从桨叶后缘脱出,尾随涡强度等于相邻两个桨叶单元的附着涡环量之差,近尾迹经过约30°方位角卷起为桨尖涡,形成远尾迹,桨尖涡强度由桨叶上的最大附着涡环量确定。对控制点施加物面法向无穿透边界条件,形成关于附着涡环量的线性方程组AΓ=B,即

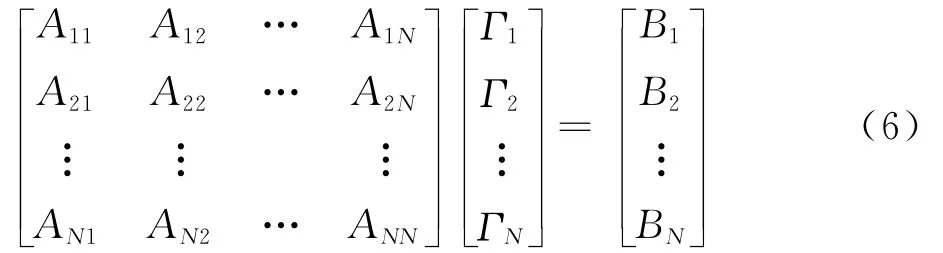
式中:A为附着涡、近尾迹和远尾迹引起的诱导速度影响系数矩阵,影响系数通过Biot-Savart定律计算;B为桨叶微段上的自由来流速度和由于旋转、挥舞等运动引起的相对速度。桨尖涡诱导产生的速度Vθ采用文献[16]中的模型:

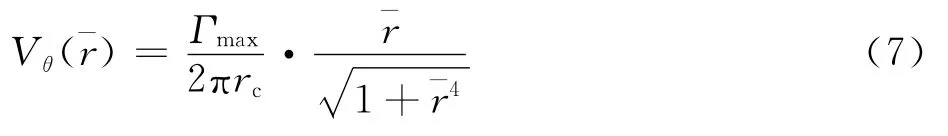
式中:Γmax=max(Γ1,Γ2,…,ΓN)为桨尖涡强度;rc为涡核半径;r-为流场中某一点与涡核中心的相对距离。

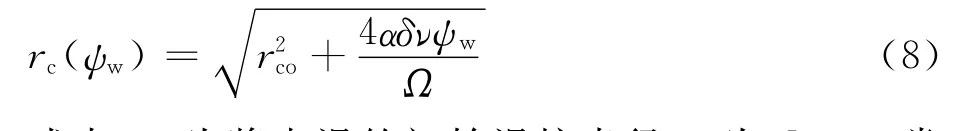
桨尖涡涡核的黏性耗散可由式(8)表示:[17]式中:rco为桨尖涡的初始涡核半径;α为Oseen常数,取α=1.256 43;涡黏性系数δ与桨尖雷诺数有关,对于模型旋翼,δ≈10;ν为空气的运动黏度,一般取ν=1.46×10-5m2/s。

在得到桨叶各单元的附着涡环量后,便可计算出相应剖面的升阻力特性,翼型气动力数据通过查表获得。

1.2 高阶谐波控制入流建模

1.1节建立的修正Beddoes尾迹模型仅适用于常规飞行状态下的旋翼气动载荷求解,本节将极坐标表示的高阶谐波入流变换到笛卡儿坐标系下,并采用时间积分推导出其对旋翼尾迹的影响。

1.2.1 高阶谐波入流引起的尾迹扭曲

噪声与桨尖涡和气动载荷存在如下关系[2]:

式中:p′(x,t)为观察点的噪声声压;Γv为桨尖涡在平行于桨叶展向的强度分量,该分量由桨尖涡强度和桨-涡干扰角度确定;L为桨叶剖面的升力;d为桨-涡垂直干扰距离。

从式(9)中可以看出,噪声声压p′(x,t)与Γv和L成正比,与d的平方成反比关系,p′(x,t)对d的变化十分敏感。

高阶谐波(n≥2)控制的幅值λin和相位Ψn可用余弦函数表达为

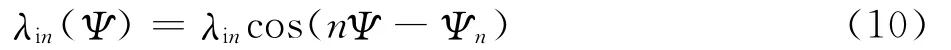
桨盘平面内由此产生的高阶谐波入流可表示为如下极坐标的形式[14]:

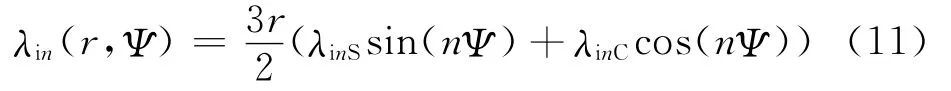
由式(11)可以得到高阶谐波引起的桨尖涡尾迹扭曲,为了便于进行时间积分,将其转化到笛卡儿坐标系下,以3阶谐波控制为例进行说明:

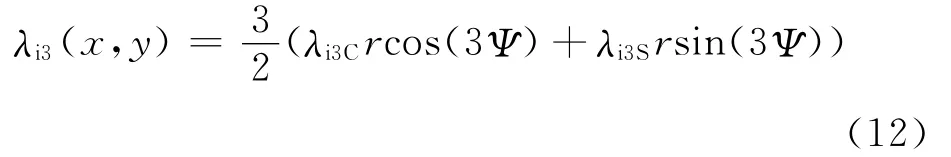
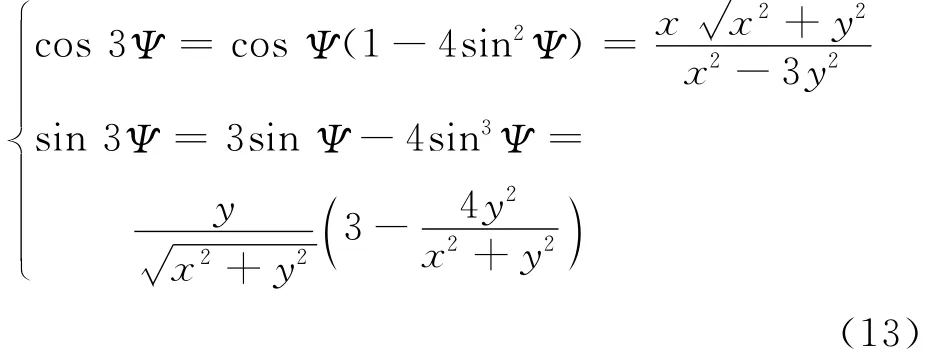
根据棣莫弗公式从桨尖涡释放点xvr开始积分,3阶谐波控制

引起的桨尖涡附加轴向位移可表示为

其他各高阶谐波产生的控制响应可用类似的方法推导得出,将其与未施加控制时的尾迹叠加,即可得到HHC控制下的尾迹形状。

1.2.2 不同阶次谐波控制效果分析

图2为谐波阶次分别为2、3和6阶时引起的桨盘平面内入流分布示意图,图中使用桨盘均匀入流系数进行了无量纲化。在桨叶旋转一周的过程中,桨叶尖部区域受入流变化的影响较桨叶内段区域更为显著。图3为一维情况下各阶谐波引起的桨尖涡附加轴向位移示意图,可以看出,相对一阶谐波(旋翼周期变距)控制输入而言,高阶谐波引起的桨尖涡附加位移较小,谐波阶次越高,其对桨尖涡运动轨迹的影响越弱,6阶以上谐波造成的影响则可以忽略不计。

1.2.3 谐波之间的耦合效应

由于各阶谐波之间的耦合效应,单一阶次的谐波输入会引起多个阶次的谐波响应。例如3阶谐波的控制输入除了直接引起桨叶上的3阶谐波响应外,还会对相邻的2阶扭转和挥舞响应产生较大的影响,这种影响可通过传递函数[18]来计入,以桨叶扭转方向为例

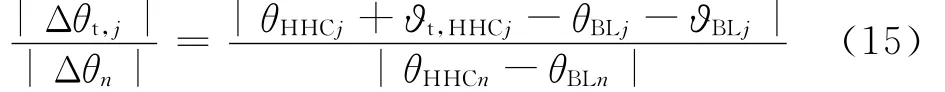
式中:θ为变距角;ϑ为弹性扭转角;下标BL表示基准状态(Baseline),j表示受n阶谐波输入影响的谐波阶次,j=n-2,n-1,…,n+2。

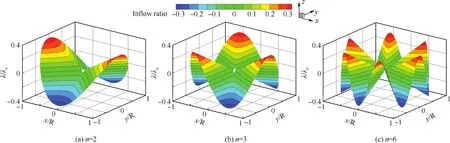
图2 桨盘平面内不同阶次的谐波入流分布(Ψn=0°)Fig.2 Inflow distribution of rotor disk with different harmonic order(Ψn=0°)

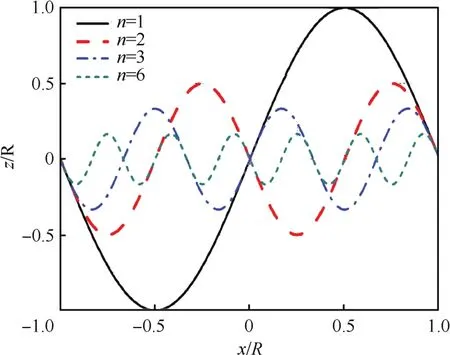
图3 谐波阶次对桨尖涡轴向位移的影响(φn=0°)Fig.3 Effect of harmonic order on tip vortex vertical displacement(φn=0°)

1.3 桨叶动力学模型

从式(15)中可以看出,传递函数由桨叶的动力学特性决定,其中扭转变形由于直接影响桨叶剖面的变距角,对高阶谐波控制的效果有着重要的影响。本文基于Hamilton原理对桨叶进行动力学建模[19]:

式中:U为桨叶上的应变能;T为动能;We为气动力和气动力矩所做的虚功。

本文计算出的HARTⅡ旋翼的前三阶挥舞振型ΦF和前二阶扭转振型ΦT分别如图4(a)和图4(b)所示,该旋翼为无铰式旋翼(相关参数见文献[20]),操纵线系的刚度通过在桨叶根部施加扭转弹簧约束的方式计入。可以看出,各挥舞振型与文献[12]中佐治亚理工学院(GIT)采用著名的多体动力学分析代码DYMORE的计算结果符合得很好,仅扭转振型在桨叶根部存在一定的误差,这可能是由于对操纵线系刚度的考虑方式不同造成的。此外,3阶的谐波控制输入与计算出的HARTⅡ桨叶基阶扭转频率3.81(文献值为3.79)相近,会产生显著的桨叶扭转响应。以上结果表明本文建立的桨叶动力学模型具有良好的精度。

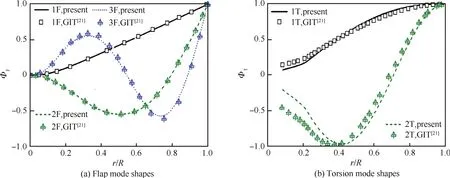
图4 HARTⅡ旋翼的挥舞和扭转振型Fig.4 Flap and torsion mode shapes of HARTⅡrotor

1.4 旋翼气动噪声计算模型

旋翼气动噪声的求解基于Williams和Hawkings建立的FW-H方程[21],该方程可精确描述整个流场区域的噪声。本文研究的桨-涡干扰状态对应的直升机前飞速度较小,旋翼流场中的跨声速效应很弱,选用忽略四极子噪声源项的F1A公式[22],有式中:p′(x,t)为噪声总声压;p′T(x,t)为厚度噪声声压;p′L(x,t)为载荷噪声声压。

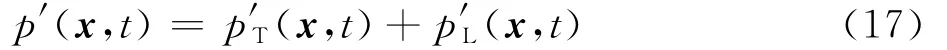
噪声声压级SPL的计算公式为

式中:SPL单位为d B;pref为参考声压,取2×10-5Pa。

2 旋翼桨-涡干扰状态的模拟及分析

2.1 桨-涡干扰状态飞行参数

本文计算的HARTⅡ旋翼斜下降飞行状态各参数分别如下:前进比μ=0.151,拉力系数CT=0.004 4,旋翼迎角αs=4.5°,航迹角γ=-6°,此时自由来流有一个垂直于桨盘向上的分量,使得桨尖涡尾迹更加靠近桨盘。该状态下旋翼总距θ0=3.8°,横向周期变距θ1c=1.92°,纵向周期变距θ1s=-1.34°。桨叶根部施加的3阶谐波激励幅值为θ3=0.86°,激励相位Ψ3在0°～360°之间变化,间隔为60°。

2.2 未施加高阶谐波控制时的桨-涡干扰状态

首先对HARTⅡ旋翼未施加高阶谐波控制时的桨-涡干扰基准状态进行了计算模拟。图5(a)为桨盘平面内的诱导入流系数分布,可以看出桨盘后半区域的诱导入流远高于桨盘前半区域,这使得图5(b)中桨尖涡在桨盘后半区域的轴向位移大于桨盘前半区域。从图5(c)预测出的桨盘平面内BVI发生位置可以看出,在前行侧50°和后行侧300°方位角附近的桨尖区域处,存在很强的桨-涡平行干扰(图中桨-涡垂直间距越小的地方用越大的图标表示)。

图6(a)为桨盘的气动载荷分布(Cn为法向力系数),气动载荷在有桨-涡干扰的桨叶方位角附近波动很显著。将0.87R桨叶剖面处的非定常气动载荷与试验值和Boyd基于CFD/CSD方法的计算值[9]进行对比,如图6(b)所示。可以看出,本文和Boyd的计算结果都有效地捕捉到了后行侧(约270°～330°桨叶方位角)的桨-涡干扰,气动载荷波动的频率和幅值均与试验值符合得较好。而在前行侧桨-涡干扰区域(约为20°～70°桨叶方位角),本文的结果能够正确反映载荷波动的趋势,但波动幅值相对试验值和文献[9]中采用CFD/CSD方法计算出的结果偏大,进一步影响了70°～120°桨叶方位角的载荷结果,这可能是由于本文采用的尾迹模型对桨叶前行侧桨-涡垂直距离预测不够精确造成的。需要指出的是,为了尽量减弱CFD方法的固有数值耗散对桨-涡干扰波动载荷的“抹平”效应,Boyd的CFD/CSD模拟中总共使用了约6 900万个网格节点,其计算在NASA的Columbia超级计算机才得以完成,计算时间仍以小时计,而本文的计算在PC上就可以实现,且计算耗时不超过1 min,因此本文建立的方法十分高效,同时具有较好的精度,适合于需要进行参数分析的高阶谐波控制规律研究及将来的工程应用。

图5 HARTⅡ旋翼桨-涡干扰飞行状态(未施加HHC)Fig.5 HARTⅡrotor BVI flight state(without HHC)

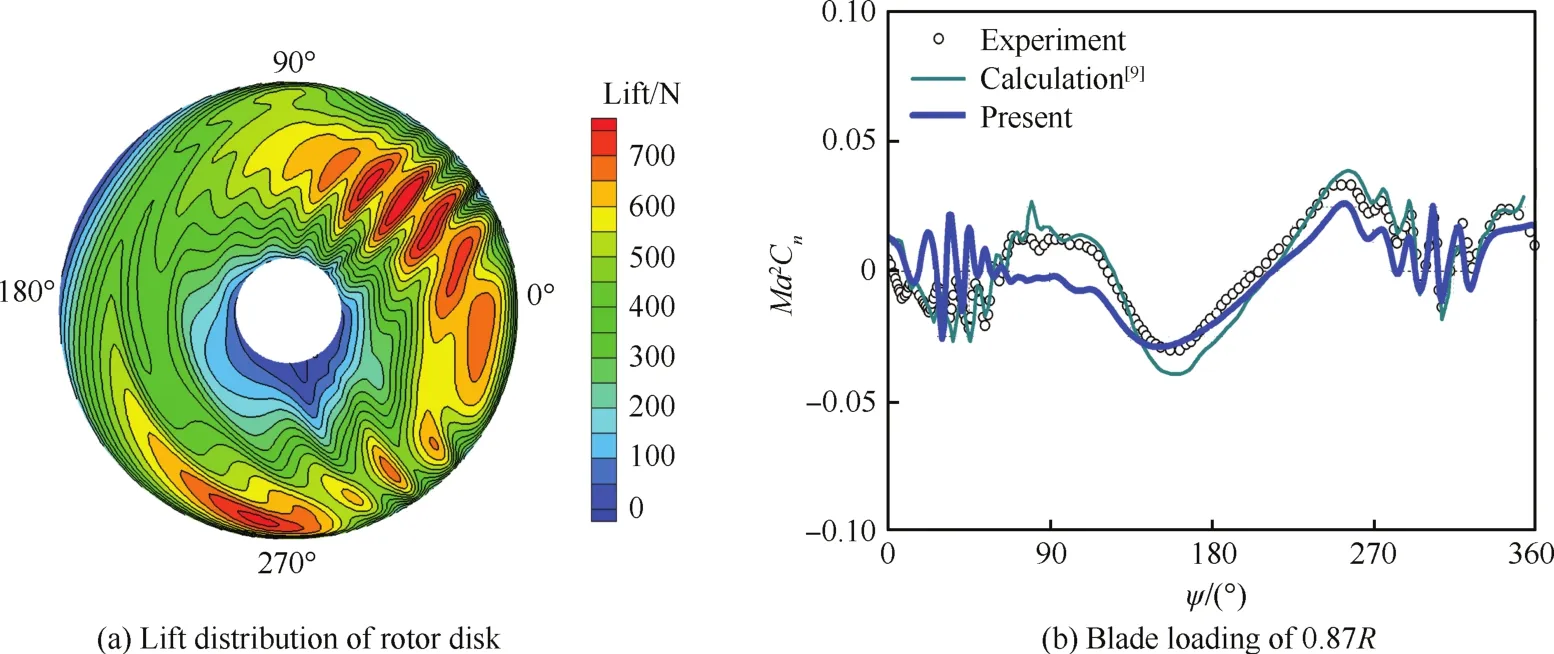
图6 HARTⅡ旋翼桨-涡干扰飞行状态气动载荷(未施加HHC)Fig.6 HARTⅡrotor loading under BVI flight state(without HHC)

2.3 施加高阶谐波控制时的桨-涡干扰状态

图7给出了不同3阶谐波控制相位下桨盘下方2.215 m平面内最大的噪声幅值SPLmax。可以看出,不同控制相位下的SPLmax差别很大,并非任意控制相位都能有效地抑制桨-涡干扰噪声。在最优噪声控制相位Ψ3=300°时,本文计算出的SPLmax=112.2 d B,比基准状态的噪声幅值(115.1 dB)小了近3 dB;而当 Ψ3=180° 时,SPLmax高达117.5 d B,超出最优控制时的噪声幅值5.3 dB,该控制相位下噪声辐射情况比基准状态更为严重。将不同控制相位下的噪声幅值与文献[9]中给出的风洞试验测得的结果相比,本文计算结果与试验值之间的误差不超过1 d B,表明本文建立的计入高阶谐波控制影响的旋翼桨-涡干扰噪声计算模型取得了较好的预测结果。

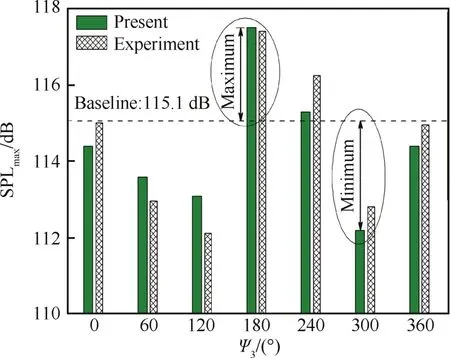
图7 不同控制相位下的最大噪声幅值Fig.7 SPLmax at different control phases

图8为最优控制和最差控制时,高阶谐波控制引起的桨尖涡在桨盘平面内的附加轴向位移。从图8(a)中可以看出,在最优控制时,在前行侧50°和后行侧300°方位角桨尖区域附近,桨尖涡附加了一个向下的轴向位移,这使得桨尖涡与桨盘平面的轴向间距相对基准状态时增大,降低了桨尖涡在桨叶表面引起的附加诱导速度,使得相应桨叶剖面的迎角振荡减弱,从而减弱非定常气动载荷的波动幅值,最终抑制辐射出的噪声。而从图8(b)最差相位控制时可以看出,桨尖涡在前后行侧附加的是向上的轴向位移,这与最优控制时的效果相反,使得BVI噪声辐射较基准状态更严重。

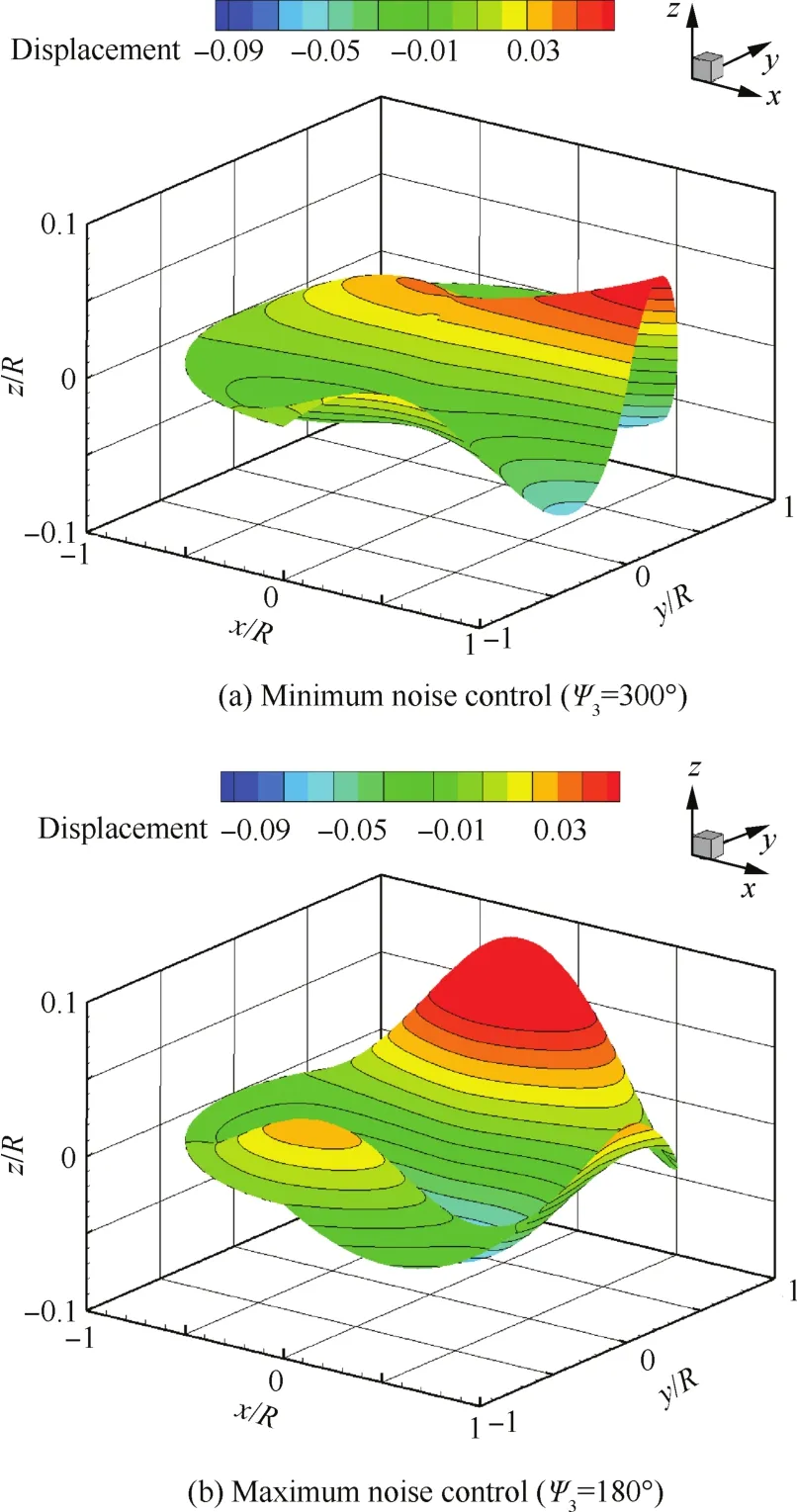
图8 HHC引起的桨尖涡附加轴向位移Fig.8 Additional tip vortex vertical displacement caused by HHC

为进一步分析采取最优和最差控制策略时二者的差异,图9给出了桨距角随桨叶方位角的变化。将基准状态下试验测出的桨距与刚性桨叶假设下的桨距输入对比可以看出,桨叶弹性扭转会降低桨距角,一个桨叶旋转周期内的平均桨距相对刚性桨叶小1°左右。加入高阶谐波控制后,在前后行侧桨-涡干扰区域,最优控制和最差控制时桨距相差约2°,前者桨距角低于基准状态,而后者高于基准状态。图10为高阶谐波控制下0.87R桨叶剖面的非定常气动载荷随方位角的变化,可以看出本文计算结果与试验值符合得较好,且施加控制时一个桨叶旋转周期内气动载荷的波动幅值比基准状态(图6(b))时大。

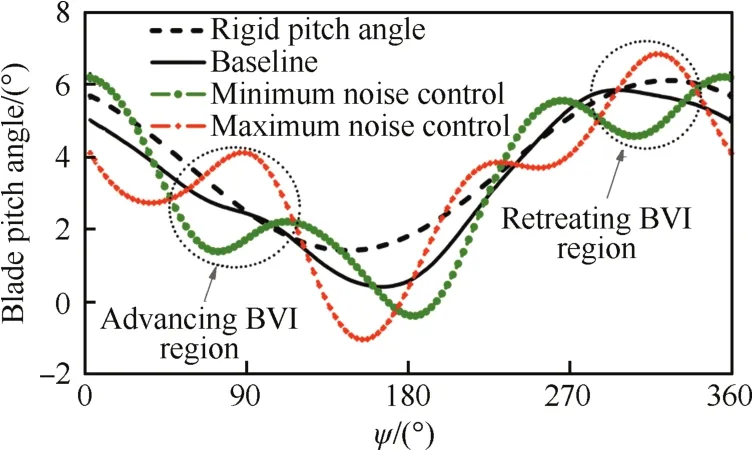
图9 不同状态下HARTⅡ旋翼的桨距角Fig.9 Blade pitch angles of HARTⅡrotor with different state

图10 施加HHC时0.87R桨叶剖面气动载荷Fig.10 Blade loading of 0.87R with HHC

3 结 论

本文基于修正Beddoes尾迹/桨叶动力学耦合模型和Farassat 1A公式,建立了一套能够计入高阶谐波控制影响的旋翼桨-涡干扰噪声数值模拟方法。采用3阶谐波控制,针对HARTⅡ旋翼在不同控制相位下的非定常气动载荷和BVI噪声进行了计算分析,得到如下结论:

1)高阶谐波控制的相位选择对旋翼桨-涡干扰噪声的控制有至关重要的影响,合理的相位输入能有效抑制噪声,若控制相位选择不当,反而会恶化桨-涡干扰噪声辐射情况。

2)高阶谐波的控制阶次越高,对尾迹的扭曲作用越小,超过六阶的高阶谐波控制起的作用可忽略不计。

3)桨叶的动力学特性尤其是扭转特性对高阶谐波控制的影响很大,当高阶谐波输入的阶次与桨叶的基阶扭转频率相近时,控制效果会大大增强。

4)高阶谐波控制主要通过改变桨-涡垂直间距来影响BVI噪声幅值,增大桨盘平面内发生桨-涡干扰方位角处的桨-涡垂直间距可有效地抑制BVI噪声。

[1] HUBBARD H H.Aeroacoustics of flight vehicles:Theory and practice[M].Melville,NY:American Institute of Physics,1995.

[2] HARDIN J C,LAMKIN S L.Concepts for reduction of blade-vortex interaction noise[J].Journal of Aircraft,1986,24(2):120-125.

[3] YU Y H,GMELIN B,SPLETTSTOESSER W,et al.Reduction of helicopter blade-vortex interaction noise by active rotor control technology[J].Progress in Aerospace Sciences,1997,33(9):647-687.

[4] WOOD E R,POWERS R W,CLINE J H,et al.On developing and flight testing a higher Harmonic control system[J].Journal of the American Helicopter Society,1985,30(1):3-20.

[5] POLYCHRONIADIS M,ACHACHE M.Higher harmonic control:Flight tests of an experimental system on SA 349 research gazelle[C]//American Helicopter Society Annual Forum,1986.

[6] WALSH D M.Flight tests of an open loop higher harmonic control system on an S-76A helicopter[D].BocaRaton:Florida Florida Atlantic University,1986.

[7] GIOVANETTI E B,HALL K C.Optimum design of compound helicopters that use higher harmonic control[J].Journal of Aircraft,2015,52(5):1-10.

[8] SPLETTSTOESSER W R,SCHULTZ K J,KUBE R,et al.A higher harmonic control test in the DNW to reduce impulsive BVI noise[J].Journal of the American Helicopter Society,1994,39(4):3-13.

[9] BOYD D D.HART-Ⅱacoustic predictions using a coupled CFD/CSD method[C]//American Helicopter Society Annual Forum,2009.

[10] 杨一栋,袁卫东.直升机随机自适应高阶谐波控制抑振研究[J].振动工程学报,1996(2):177-181.YANG Y D,YUAN W D.Study of helicopter vibration reduction technique with stochastic adaptive HHC[J].Journal of Vibration Engineering,1996(2):177-181(in Chinese).

[11] 冯剑波,陆洋,徐锦法,等.旋翼桨-涡干扰噪声开环桨距主动控制研究[J].航空学报,2014,35(11):2901-2909.FENG J B,LU Y,XU J F,et al.Research on the effect of open-loop active blade pitch control on rotor BVI noise alleviation[J].Acta Aeronautica et Astronautica Sinica,2014,35(11):2901-2909(in Chinese).

[12] WALL B G,LIM J W,SMITH M J.An assessment of comprehensive code prediction state-of-the-art using the HARTⅡinternational workshop data[C]//American Helicopter Society Annual Forum,2012.

[13] WALL B G.Prescribed wake modifications to account for harmonic rotor loading and validation with HART data[C]//American Helicopter Society Annual Forum,2011.

[14] WALL B G.Helicopter rotor BVI airloads computation using advanced prescribed wake modeling[C]//29th AIAA Applied Aerodynamics Conference,2011.

[15] BEDDOES T S.A wake model for high resolution airloads[C]//International Conference on Rotorcraft Basic Research,1985.

[16] LEISHMAN J G.Principles of helicopter aerodynamics[M].Cambridge:Cambridge University Press,2006.

[17] BHAGWAT M J,LEISHMAN J G.Generalized viscous vortex model for application to free-vortex wake and aeroacoustic calculations[C]//American Helicopter Society Annual Forum,2002.

[18] WALL B G.The effect of HHC on the vortex convection in the wake of a helicopter rotor[J].Aerospace Science&Technology,2000,4(5):321-336.

[19] YUAN K A,FRIEDMANN P P.Aeroelasticity and structural optimization of composite helicopter rotor blades with swept tips:NASA Report 4665[R].Washington,D.C.:NASA,1995.

[20] WALL B G.2nd HHC Aeroacoustic rotor test(HART-Ⅱ)-Part 1:Test documentation:Report IB 111-2003/31[R].Cologne:German Aerospace Center Institute,2003.

[21] WILLIAMS J E F,HAWKINGS D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Philosophical Transactions of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,1969,264(1151):321-342.

[22] FARASSAT F.Derivation of formulations 1 and 1A of Farassat:NASA TM-2007-214853[R].Washington,D.C.:NASA,2007.

lnfluence of higher harmonic control on airload and acoustics of rotor blade-vortex interaction

WANG Liangquan,XU Guohua*,SHl Yongjie,XlA Runze

National Key Laboratory of Science and Technology on Rotorcraft Aeromechanics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

Harsh blade-vortex interaction(BVl)noise will be generated when a helicopter is flying at a moderate speed level flight or descending.Based on the modified Beddoes wake/blade structural dynamics coupling model and Farassat 1A formula,a rotor BVl airload and acoustics prediction method is proposed,in which the influence of higher harmonic control(HHC)can be included.The additional tip vortex vertical displacement caused by HHC is derived from time integration of higher harmonic inflow,and a transfer function that relates single HHCinput to resulting response at the same and neighboring frequencies is identified by blade dynamic characteristics.The rotor airload of the baseline case in higher harmonic control aeroacoustics rotor TestⅡ(HARTⅡ)is investigated and compared with experimental data firstly.The influencing mechanism and varying pattern of the rotor acoustic property at different 3/Rev control phases is then assessed.The results show that blade dynamic characteristics,especially torsional behaviors,are important for effectiveness of higher harmonic control.Selection of HHC phase input is significant to BVl noise control,and irrational HHC phase input will worsen noise radiation.

higher harmonic control;helicopter;rotor;blade-vortex interaction;aerodynamic loading;noise

2016-10-13;Revised:2017-02-19;Accepted:2017-02-28;Published online:2017-03-20 15:15

URL:www.cnki.net/kcms/detail/11.1929.V.20170320.1515.012.html

s:Funding of Jiangsu lnnovation Program for Graduate Education(KYLX16_0389);Priority Academic Program Development of Jiangsu Higher Education lnstitutions

V211.52

A

1000-6893(2017)07-520847-10

10.7527/S1000-6893.2017.520847

2016-10-13;退修日期:2017-02-19;录用日期:2017-02-28;网络出版时间:2017-03-20 15:15

www.cnki.net/kcms/detail/11.1929.V.20170320.1515.012.html

江苏省普通高校研究生科研创新计划项目(KYLX16_0389);江苏高校优势学科建设工程基金

*通讯作者.E-mail:ghxu@nuaa.edu.cn

王亮权,徐国华,史勇杰,等.高阶谐波控制对旋翼桨-涡干扰载荷和噪声的影响[J].航空学报,2017,38(7):520847.WANG L Q,XU GH,SHl Y J,et al.lnfluence ofhigher harmonic control on airload and acoustics ofrotor blade-vortex interaction[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):520847.

(责任编辑:鲍亚平,苏磊)

*Corresponding author.E-mail:ghxu@nuaa.edu.cn