弹性空腔流致噪声/结构振动特性试验

王显圣*,杨党国刘俊施傲,周方奇,吕彬彬

1.中国空气动力研究与发展中心空气动力学国家重点实验室,绵阳 621000

2.中国空气动力研究与发展中心高速空气动力研究所,绵阳 621000

弹性空腔流致噪声/结构振动特性试验

王显圣1,2,*,杨党国1,2,刘俊1,2,施傲2,周方奇2,吕彬彬2

1.中国空气动力研究与发展中心空气动力学国家重点实验室,绵阳 621000

2.中国空气动力研究与发展中心高速空气动力研究所,绵阳 621000

高速空腔中经常存在高强度且多频率分量的流致噪声,空腔噪声与结构振动之间耦合效应严重,甚至可能发生结构共振。为此,在0.6 m×0.6 m高速风洞中,通过调整空腔底板厚度,改变其结构固有频率,模拟空腔流致噪声/振动相互作用。利用脉动压力和振动加速度测试技术,获取亚跨声速条件下,弹性空腔流致噪声特性及其结构振动响应特性。马赫数变化范围为0.6～1.2。结果表明,当振动强度较弱时,结构振动对空腔噪声影响较小,而空腔噪声对结构振动影响较大,在噪声载荷主频位置,振动谱出现峰值并且噪声/振动相关性达到最强;此外,空腔结构振动还与其固有频率特性密切相关,振动主要以低阶模态为主。

弹性空腔;流致噪声;气动声学;结构振动;风洞试验

在航空航天领域,空腔结构普遍存在于各类飞行器部件中,如内埋武器舱、飞机起落架舱等,其在提高飞行器隐身性能以及降低飞行阻力等方面具有重要作用。然而,高速来流条件下,空腔中经常存在高强度且多频率分量的噪声载荷[1],能够使空腔薄壁结构产生弹性变形,加速其疲劳破坏,甚至导致结构共振,危及飞行器系统结构安全和作战效能提高。因此,弹性空腔流致噪声与结构振动耦合特性研究,对于探索飞行器非定常流动/振动/噪声耦合机理等前沿基础问题,以及内埋武器舱结构优化设计等工程实际问题具有重要的研究意义。

空腔噪声与流激振荡现象密切相关,并具有明显的非定常和非线性特征[2]。空腔前缘涡扰动在剪切层不稳定性作用下不断增长,当涡扰动撞击空腔后缘时,流场中辐射声波,腔内形成多波叠加的扰动传播方式,当波前传至边界层分离区时,流场中产生新的扰动并形成反馈回路,引起流动自持振荡。从20世纪50年代开始,国内外机构对该问题开展了大量研究[3-4]。Rossiter[5]基于这种观点建立振荡频率预估模型,取得了与试验一致的结果。不过,在Rossiter模型中,腔内声波前传速度利用来流声速表述,根据腔内温度测量结果,二者并不相等,故而 Heller等[6]对Rossiter模型进行了修正,扩展了其适用范围。空腔流激振荡现象主要受到空腔几何形状和来流条件等因素的影响(如空腔长深比、长宽比、来流马赫数、雷诺数和边界层型态等)。Stallings和 Wilcox[7]通过风洞试验发现空腔长深比是影响流动自持振荡的主要因素,随着长深比不同,空腔开口区域剪切层型态发生明显变化,并撞击到腔内不同区域。Beresh[8]和Arunajatesan[9]等结合试验和数值方法研究了不同长宽比的三维空腔流动特性,当空腔宽度较小时,侧壁附近的流向涡影响了剪切层不稳定特性。空腔流激振荡现象还与剪切层不稳定性密切相关,当空腔前缘边界层发生分离以后,剪切层两侧存在较大速度差,剪切层高度敏感,涡扰动在运动过程中不断增长,形成反馈回路[10]。Bian等[11]采用高时间分辨率PIV(Particle Image Velocimetry)技术研究剪切层中涡扰动的不稳定增长特性,分析了流动结构相干特性和涡/固壁相互作用机制。Bres[12]和Crook[13]等对空腔流动三维特性进行了分析,在腔内外不均匀压力场作用下,流向涡导致流动不稳定性增强,同时改变了空腔流场自持振荡特性。Zhuang等[14]发现空腔剪切层中涡扰动增长特性受前缘射流显著影响,该方法对气动噪声具有明显抑制效果,不过Sahoo[15]和Li[16]等发现为使控制效果达到最佳,需要合理选择射流质量和动量注入率。Ukeiley等[17]分析了抑制涡扰动的不稳定增长特性和改变空腔剪切层型态2种控制方法的作用机理,发现外加控制措施通常能够改变剪切层运动轨迹,但是基于改变剪切层不稳定性的控制方法可能在效率方面更具优势。

固壁对流动结构的约束是空腔流致噪声以及流激振荡产生的关键。为了减弱了剪切层旋涡与空腔后壁的撞击,Dudley和Ukeiley[18]通过在空腔前缘边界层中放置圆柱改变剪切层的运动轨迹,有效降低了腔内噪声强度。相似地,Williams等[19]利用空腔后壁修型技术分析了减弱剪切层旋涡-固壁相互作用对空腔噪声的影响机制。Rowley和Colonius[20]通过分析空腔前缘边界层尺度对流场剪切层型态和不稳定性的影响机制,研究了空腔流动自持振荡的剪切层模态和尾迹模态形成机理。Ukeiley和Murray[21]利用PIV技术研究了剪切层与空腔固壁的相互作用,指出剪切层旋涡与空腔几何尺度的比例关系是影响空腔流动振荡模态的重要因素。Liu和Katz[22]通过分析涡-固壁相互作用,发现剪切层低频运动对于空腔流动自持振荡具有重要影响。Zhang[23]研究了剪切层型态以及腔内波系演化,发现流场剪切层与空腔后壁撞击改变了空腔内外质量交换,故而影响空腔流动自持振荡和腔内压力反馈机制。

近年来,国内在空腔非定常流动以及流致噪声特性研究方面也取得了较大进步。罗柏华等[24]利用纯声激励技术改变空腔前缘边界层的分离特性,在低亚声速空腔流动中,通过声激励影响剪切层内不稳定波的发展,改变了剪切层中扰动的强度和频率特性,有效抑制了腔内脉动压力强度。侯中喜等[25]通过求解Navier-Stokes方程对高速来流条件下空腔的非定常流动特性进行分析,研究了三维流动特征对空腔自持振荡的影响。张强[26]利用试验结果对小尺寸空腔振荡模态预估方法进行了分析,并依据不同来流马赫数研究空腔发声机理,对延迟因子进行修正,提出空腔自持振荡模态预估方法。司海青和王同光[27]通过数值求解非定常雷诺平均方程,研究了层流与湍流入口条件对于三维空腔流动自持振荡特性的影响。李晓东等[28]通过求解二维URANS(Unsteady Reynolds-Averaged Navier-Stokes)方程研究亚声速空腔自持振荡的发声机理,分析了流动自持振荡的频率特性以及来流边界层的影响规律。杨党国等[29]通过风洞试验研究了后壁倒角情况下的空腔噪声特性,结果显示,存在倾角时空腔后壁与剪切层相互作用减弱,腔内噪声得到有效抑制。万振华等[30]采用直接数值模拟(Direct Numerical Simulation,DNS)方法研究了低雷诺数方腔流动自持振荡现象及其诱导噪声特性,分析了剪切层不稳定性的影响机制,并采用正交分解(Proper Orthogonal Decomposition,POD)方法研究不同频率分量对于空腔流动特性的影响。李环等[31]等研究了低速空腔流动自持振荡现象,通过PIV技术显示出空腔流动自持振荡的剪切层和尾迹模态。吴继飞等[32]利用高速风洞试验研究剪切层扰流法对空腔流场的气动声学特性影响,在跨声速来流条件下显著改善了空腔内的噪声环境。王一丁等[33]结合非线性噪声与RANS(Reynolds-Averaged Navier-Stokes)方程求解技术,分析了前缘射流对空腔流动自持振荡的影响机制,通过气帘喷流技术改变超声速空腔剪切层型态,有效降低了腔内噪声强度。

在弹性壁约束下,空腔流致噪声与结构振动之间存在相互作用,该问题中空腔噪声场存在振动边界条件,显著增加了数值和理论研究的复杂程度[34]。为此,本文通过风洞试验模拟弹性空腔声/振相互作用,获取亚跨声速弹性空腔流致噪声与结构振动相互作用特性,研究振动边界对于空腔气动噪声特性的影响,并分析腔体结构振动与非定常流致噪声特性、结构固有属性的关系。

1 试验方法与设备

试验在中国空气动力研究与发展中心的FL-23风洞完成,通过调节空腔底板厚度改变其结构固有频率,利用脉动压力传感器和振动加速度传感器,获取模型表面噪声载荷与结构振动响应特性,并采用相关分析等手段,研究弹性空腔流致噪声/振动特性。

1.1 风洞设备

FL-23风洞是一座直流暂冲式亚、跨、超声速风洞[35],来流马赫数可达0.4～4.0,来流总压为95～720 k Pa,单位长度雷诺数为(9.87～28.7)×106m-1。试验段截面尺寸为0.6 m×0.6 m,长度为2.5 m。风洞试验段洞壁可根据试验类型更换,跨声速试验时上下壁为斜开孔壁、左右壁为实壁,超声速试验时试验段四壁均为实壁。

1.2 试验模型

空腔模型安装于风洞侧壁,气流方向为从右向左,如图1所示。其中,空腔长度L为540 mm,空腔深度D为90 mm,空腔宽度W 为360 mm,空腔长深比L/D=6,空腔长宽比L/W=1.5。采用厚度为25 mm与4 mm的钢板作为空腔底板,模拟刚性空腔和弹性空腔,底板四边采用固支方式。

根据Stallings和Wilcox[7]的研究结果,在亚跨声速来流条件下,该类空腔流动属于开式流动范围,空腔前缘的边界层分离以后,所形成的腔开口区域的剪切层将再附于空腔后壁,引起流激振荡并诱发气动噪声[2]。在弹性固壁区域,噪声载荷产生交变应力,能够直接作用于固壁,并引起结构振动,同时结构振动也会改变空腔声场的边界条件。

1.3 测试设备与方法

采用脉动压力传感器(型号:Kulite,LE-062-15A)测量空腔底板表面噪声载荷特性,传感器直径为1.7 mm,其安装位置如图2所示,其中,X为传感器与空腔前缘边界之间的距离。采用振动加速度传感器(型号:EGAX-100-C20001)测量空腔底板振动响应,振动传感器安装于空腔底板中心位置。空腔底板噪声载荷与结构振动加速度测试数据均采用DEWETRON-2601进行实时采集和存储,采样频率为50 k Hz,采样时间为10 s。

描述空腔噪声强度的主要参数包括脉动压力均方根prms、总声压级OASPL和脉动压力系数Cp,具体参数如下。

脉动压力均方根值:

式中:t为时间;T为采样时间;p(t)为非定常脉动压力幅值;脉动压力参考值pref=2×10-5Pa;q为来流动压。

功率谱密度是描述脉动压力能量随频率分布的函数。采用经典功率谱密度估计方法,根据式(3)对脉动压力数据进行变换后得到,功率谱密度函数P(f)和声压功率谱函数SPFS为

2 刚性空腔流致噪声特性

试验来流马赫数为0.6～1.2,空腔长深比L/D=6,来流总压为102.4～125.3 k Pa,雷诺数(基于空腔长度)为(6.5～10.7)×106。采用厚度为25 mm的钢板作为刚性空腔底板,研究刚性空腔模型表面的噪声载荷特性。

空腔噪声载荷特性与空腔流动特征密切相关,当来流边界层在空腔前缘发生分离以后,空腔开口区域形成剪切层,剪切层逐渐演化并与空腔后壁相互作用,引起流场中产生强烈的气动噪声。根据噪声相关性分析结果[10,17-18],腔内不同区域之间的噪声具有较强的相关性,噪声能量以扰动形式从空腔后壁区域不断向空腔流场其他区域传播。Rossiter[5]和Heller等[6]对空腔流激振荡的产生机理进行了深入分析,提出半经验公式对空腔噪声频率成分进行预测,频率对应无量纲斯特劳哈尔数St为St=f L/U∞,其中U∞为来流速度,模型对应预测公式为

式中:Ma为来流马赫数;m为阶数;γ为空气比热比;α和κ为经验系数,α=0.25,κ=0.57。两种模型对空腔流动的非定常和非线性特征进行了较大简化[36],因此式(6)～式(7)的预测结果与试验结果相比存在一定误差。尽管如此,由于Rossiter与Heller模型有效捕捉了空腔流激振荡的主要特征,仍得到了国内外研究组的数据支持[12,29]。

图3为不同来流马赫数下刚性空腔模型表面的噪声声压级分布情况。在Ma=1.2和0.9两种工况下,声压级曲线基本一致,在腔后部区域,声压级达174 d B,显著高于Ma=0.6的情况。噪声强度在腔内不同区域之间也存在显著差异。在空腔前部,模型表面噪声声压级较低,值得注意的是其最低位置处于X/L约为0.2处,而不在最靠近空腔前壁区域;在空腔后部,噪声声压级随测点靠近后壁呈现整体升高趋势,最靠近空腔后壁测点的声压级最高。这种气动声学特征与空腔前缘和后缘的流动特性密切相关,在空腔前部区域,流场中存在较强的涡流和流动分离现象[10],在固壁约束下,流场速度较低,相应噪声强度较弱;在空腔后部区域,由于剪切层直接作用于空腔固壁并产生强烈噪声,噪声携带的能量以扰动形式从腔后壁传向其他区域[14,17],而传播过程中能量逐渐衰减,导致空腔后壁区域的噪声强度较高。

空腔底板区域的噪声载荷功率谱曲线如图4所示,测点位于X/L=0.97处。由于腔内存在较强的流激振荡现象,空腔噪声载荷谱中出现多个峰值,在腔后部和中部区域,噪声功率谱的峰值高于前部区域。表1为空腔噪声载荷功率谱各阶峰值频率对应St数的试验与模型预测结果比较。当来流马赫数为0.9时,空腔噪声载荷的功率谱曲线最高峰值对应的主频St=0.66,与二阶Rossiter频率预测结果相符。在高频区域,模型预测结果与试验结果偏差增大,可能由于随着特征频率增加,流动非定常、非线性特征增加,空腔流动除了受到Rossiter等所述流激振荡影响外,还存在如驻波等其他影响机制并且其作用效果增强[37]。

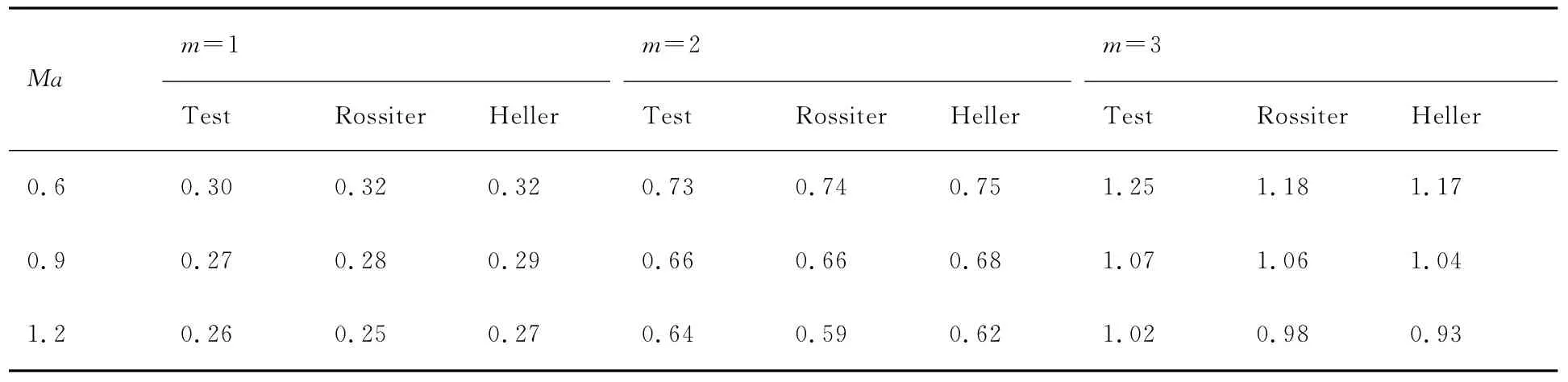
表1 刚性空腔噪声St数的试验、Rossiter模型与Heller模型预测结果Table 1 Predicted results of strouhal number of rigid cavity noises obtained from test，Rossiter and Heller models

图5比较了刚性空腔噪声的功率谱峰值频率对应St数的试验与模型预测结果的差别尽管Rossiter和Heller模型中半经验系数存在一些改进算法[14,38],不过本文采用Rossiter提出的原始半经验系数[5-6],腔内噪声频率成分与模型预测结果基本吻合。当来流马赫数较高时,两个模型的预测结果的偏差增大,这是由于Heller模型考虑了腔内温度变化所引起扰动波传播速度的改变,在高马赫数来流条件下,其预测结果与试验数据更加吻合,如表1所示。

3 弹性空腔流致噪声与结构振动特性

高速来流条件下,弹性空腔受到模型表面噪声载荷的激励,声压引起的交变应力使结构产生振动,改变了声场的边界条件,从而形成弹性空腔流致噪声/振动相互作用。为此,采用厚度为4 mm的钢板作为空腔底板,模拟弹性空腔模型,利用脉动压力与振动加速度传感器,获取模型表面噪声载荷与腔体结构振动响应特性。通过敲击法测量空腔底板固有频率,其基频测量结果约为197 Hz,如表2所示。

图6为弹性空腔噪声声压级与刚性空腔相比的差值沿底板中心线的分布情况。在本次试验条件下,底板结构振动对腔内噪声特性影响较小,与刚性空腔情况相比,噪声总声压级变化量在±0.5 d B以内。图7比较了弹性空腔与刚性空腔模型表面噪声功率谱曲线,其中fb为空腔底板的基频(单位为Hz),2种工况下曲线趋于重合。可以发现,在本文试验条件下,空腔底板振动强度较弱,由于其振动幅度较小,其辐射声波的强度与腔内噪声能量相比较弱,因此导致空腔噪声载荷特性受到腔底板振动的影响较小。

表2 弹性空腔底板的固有频率Table 2 Natural frequency of elastic cavity floor

图8比较了弹性空腔与刚性空腔底板的振动加速度均方根随来流马赫数的变化曲线,其中arms为空腔底板振动测点的加速度均方根值,g为当地重力加速度。在刚性空腔情况下,结构振动强度较弱,振动加速度均方根的最大值约为2.2 m/s2。在弹性空腔情况下,空腔底板较薄,更容易发生振动,当来流马赫数为1.2时,底板的振动加速度均方根值达84.6 m/s2,相比刚性空腔情况增大了38.5倍,说明刚性空腔底板较厚,其振动强度较弱,更接近于固壁条件,而弹性空腔则存在较强的振动边界。

在亚跨声速条件下,弹性空腔底板振动加速度随来流马赫数升高而增大,并在Ma=1.2时达到最高值。根据腔内噪声的声压级分布曲线(如图3所示),空腔底板的噪声载荷在Ma=0.6时最小,在Ma=0.9,1.2时相近。从振动加速度曲线(如图8所示)可以发现,Ma=1.2时弹性空腔底板的振动加速度明显高于Ma=0.9情况,说明腔内噪声强度不是影响结构振动强度的唯一因素,结构振动还与空腔噪声频谱特性相关。

图9比较了弹性空腔底板的振动加速度功率谱随St数的变化曲线,其中apsd为振动测点加速度的功率谱密度,可以发现,振动加速度功率谱存在多个峰值,振动谱的峰值出现在腔内噪声载荷峰值频率以及结构固有频率位置。在噪声载荷峰值频率位置,振动谱中相应峰值的大小存在较大差异,说明噪声载荷不同频率成分对结构振动的作用效果不同;在结构固有频率位置,空腔底板的振动谱出现峰值,说明弹性空腔的结构振动特性除了受到腔内噪声载荷的影响外,还受到其结构固有属性的影响。

4 空腔结构振动与噪声载荷相关性分析

弹性空腔噪声载荷与结构振动加速度的互功率谱密度分布曲线如图10所示,其中虚线对应噪声载荷谱峰值频率,归一化的互功率谱系数Cxy采用如下公式获得:

式中:Gxy为弹性空腔模型表面噪声载荷(测点:X/L=0.5)与结构振动测点加速度的互功率谱密度。空腔底板的结构振动与噪声载荷之间具有高度相关性,在噪声载荷的主频位置,二者相关系数达到峰值,说明弹性空腔底板振动受到噪声载荷的显著影响,结构振动与噪声激励源的频谱特性密切相关。

在不同来流马赫数下,空腔声/振互谱曲线的最高峰值对应的频率模态有所差别,Ma=0.6情况对应噪声载荷的2阶频率模态,而Ma=0.9与Ma=1.2情况均对应噪声载荷的3阶频率模态,这是因为这些模态反映了噪声激励源最主要的频率成分,其引起的结构振动较强,从而导致这些频率位置处,空腔噪声载荷与结构振动之间的相关性达到最强。在噪声载荷的其他频率成分以及整个宽频区域,声/振相关系数值较小,根据前文分析结果,腔体结构振动在结构固有频率位置仍然较强,说明尽管弹性空腔结构振动与其结构固有属性密切相关,然而腔体结构振动特性与激励源在结构固有频率位置的相关性较弱,可能受到空腔噪声宽频成分的影响更加显著。

5 结 论

1)通过亚跨声速风洞试验,研究弹性/刚性空腔模型表面的噪声载荷与结构振动特性,在当前工况下,腔体结构振动对于空腔噪声声压级及其功率谱特性影响较小。

2)在噪声载荷激励下,弹性空腔底板的振动加速度谱中包含不同频率成分,振动谱在结构固有频率位置出现峰值,此时结构振动特性与激励源的相关性较弱,主要受到腔体结构固有属性影响。

3)弹性空腔的结构振动与空腔噪声载荷的频谱特性密切相关,在噪声载荷主频位置,结构振动谱出现峰值,并且结构振动与模型表面噪声载荷的主频成分相关性最强。

致 谢

感谢中国空气动力研究与发展中心高速空气动力研究所的杨可工程师、闫煜工程师在试验过程中的帮助,以及梁锦敏助理研究员在数据处理过程中的讨论。

[1] SEINER J M,JANSEN B J,MURRAY N E.Weapons bay acoustic suppression at Mach 2:AIAA-2008-0060[R].Reston:AIAA,2008.

[2] WAGNER J L,BERESH S J,CASPER K M,et al.Relationship between transonic cavity tones and flowfield dynamics using pulse-burst PIV:AIAA-2016-1345[R].Reston:AIAA,2016.

[3] ROWLEY C W,WILLIAMS D R.Dynamics and control of high-Reynolds-number flow over open cavities[J].Annual Review of Fluid Mechanics,2006,38(1):251-276.

[4] SHANKAR P N,DESHPANDE M D.Fluid mechanics in the driven cavity[J].Annual Review of Fluid Mechanics,2000,32(1):93-136.

[5] ROSSITER J E.Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds:No.3438[R].Aeronautical Research Council Reports and Memoranda,1964.

[6] HELLER H H,HOLMES D G,COVERT E E.Flow-induced pressure oscillations in shallow cavities[J].Journal of Sound and Vibration,1974,18(4):545-553.

[7] STALLINGS R L J,WILCOX F J J.Experimental cavity pressure distributions at supersonic speeds:NASA Technical Paper-2683[R].Washington,D.C.:NASA,1987.

[8] BERESH S J,WAGNER J L,PRUETT B O M,et al.Supersonic flow over a finite-width rectangular cavity[J].AIAA Journal,2015,53(2):296-310.

[9] ARUNAJATESAN S,BARONE M F,WAGNER J L,et al.Joint experimental/computational investigation into the effects of finite width on transonic cavity flow:AIAA-2014-3072[R].Reston:AIAA,2014.

[10] SCHMIT R F,GROVE J E,SEMMELMAYER F,et al.Nonlinear feedback mechanisms inside a rectangular cavity[J].AIAA Journal,2014,52(10):2127-2142.

[11] BIAN S,DRISCOLL J F,ELBING B R,et al.Time resolved flow-field measurements of a turbulent mixing layer over a rectangular cavity[J].Experiments in Fluids,2011,51(1):51-63.

[12] BRES G A,COLONIUS T.Three-dimensional instabilities in compressible flow over open cavities[J].Journal of Fluid Mechanics,2008,599(90):309-339.

[13] CROOK S D,LAU T C W,KELSO R M.Three-dimensional flow within shallow,narrow cavities[J].Journal of Fluid Mechanics,2013,735(11):587-612.

[14] ZHUANG N,ALVI F S,ALKISLAR M B,et al.Supersonic cavity flows and their control[J].AIAA Journal,2006,44(9):2118-2128.

[15] SAHOO D,ANNASWAMY A,ZHUANG N,et al.Control of cavity tones in supersonic flow:AIAA-2005-0793[R].Reston:AIAA,2005.

[16] LI W,NONOMURA T,FUJII K.Mechanism of controlling supersonic cavity oscillations using upstream mass injection[J].Physics of Fluids,2013,25(8):545-553.

[17] UKEILEY L S,PONTON M K,SEINER J M,et al.Suppression of pressure loads in cavity flows[J].AIAA Journal,2004,42(1):70-79.

[18] DUDLEY J G,UKEILEY L.Passively controlled supersonic cavity flow using a spanwise cylinder[J].Experiments in Fluids,2014,55(9):1-22.

[19] WILLIAMS D R,FABRIS D,MORROW J.Experiments on controlling multiple acoustic modes in cavities:AIAA-2000-1903[R].Reston:AIAA,2000.

[20] ROWLEY C W,COLONIUS T.On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities[J].Journal of Fluid Mechanics,2002,455(455):315-346.

[21] UKEILEY L,MURRAY N.Velocity and surface pres-sure measurements in an open cavity[J].Experiments in Fluids,2005,38(5):656-671.

[22] LIU X,KATZ J.Vortex-corner interactions in a cavity shear layer elucidated by time-resolved measurements of the pressure field[J].Journal of Fluid Mechanics,2013,728(4):417-457.

[23] ZHANG X.Compressible cavity flow oscillation due to shear layer instabilities and pressure feedback[J].AIAA Journal,1995,33(8):1404-1411.

[24] 罗柏华,胡章伟,戴昌晖.声激励抑制空腔流激振荡的实验研究[J].南京航空航天大学学报,1999,31(1):1-4.LUO B H,HU Z W,DAI C H.Experimental study on suppression of cavity flow oscillations by means of acoustic excitation[J].Journal of Nanjing University of Aeronautics and Astronautics,1999,31(1):1-4(in Chinese).

[25] 侯中喜,夏刚,秦子增.三维超声速开式空腔振荡特性研究[J].国防科学技术大学学报,2004,26(6):1-4.HOU Z X,XIA G,QIN Z Z.The numerical analysis of oscillatory characteristics in 3D supersonic open cavity[J].Journal of National University of Defense Technology,2004,26(6):1-4(in Chinese).

[26] 张强.流动诱导空腔振荡频率方程的改进[J].振动工程学报,2004,17(1):53-57.ZHANG Q.Improvements on the governing equation of frequencies of cavity flow induced oscillations[J].Journal of Vibration Engineering,2004,17(1):53-57(in Chinese).

[27] 司海青,王同光.边界条件对三维空腔流动振荡的影响[J].南京航空航天大学学报,2006,38(5):595-599.SI H Q,WANG T G.Influence of boundary conditions on 3D cavity flow induced oscillations[J].Journal of Nanjing University of Aeroacoustics and Astronautics,2006,38(5):595-599(in Chinese).

[28] 李晓东,刘靖东,高军辉.空腔流激振荡发生的数值模拟研究[J].力学学报,2006,38(5):599-604.LI X D,LIU J D,GAO J H.Numerical simulation of flow-induced oscillation and sound generation in a cavity[J].Chinese Journal of Theoretical and Applied Mechanics,2006,38(5):599-604(in Chinese).

[29] 杨党国,范召林,李建强,等.后壁倒角对空腔噪声的抑制效果[J].实验流体力学,2010,24(5):22-25.YANG D G,FAN Z L,LI J Q,et al.Suppression effects of rear-face angle of cavity on its aerodynamics noise[J].Journal of Experiments in Fluid Mechanics,2010,24(5):22-25(in Chinese).

[30] 万振华,周林,孙德军.方腔流致振荡及噪声的数值研究[J].空气动力学报,2012,30(3):291-298.WAN Z H,ZHOU L,SUN D J.Numerical investigation of flow induced oscillations and noise in a rectangular cavity[J].Acta Aerodynamica Sinica,2012,30(3):291-298(in Chinese).

[31] 李环,方涛,吴方良,等.不可压缩空腔流的振荡模式[J].力学学报,2013,45(5):782-786.LI H,FANG T,WU F L,et al.The oscillation mode of incompressible cavity flow[J].Chinese Journal of Theoretical and Applied Mechanics,2013,45(5):782-786(in Chinese).

[32] 吴继飞,徐来武,范召林,等.开式空腔气动声学特性及其流动控制方法[J].航空学报,2015,36(7):2155-2165.WU J F,XU L W,FAN Z L,et al.Aeroacoustic characteristics and flow control method of open cavity flow[J].Acta Aeronautica et Astronautica Sinica,2015,36(7):2155-2165(in Chinese).

[33] 王一丁,郭亮,童明波,等.高速飞行器空腔脉动压力主动控制与非线性数值模拟[J].航空学报,2015,36(1):213-222.WANG Y D,GUO L,TONG M B,et al.Active control and nonlinear numerical simulation for oscillating pressure of high-speed aircraft cavity[J].Acta Aeronautica et Astronautica Sinica,2015,36(1):213-222(in Chinese).

[34] WAGNER J L,CASPER K M,BERESH S J,et al.Fluid-structure interactions in compressible cavity flows[J].Physics of Fluids,2015,27(6):152-165.

[35] 李周复.风洞实验手册[M].北京:航空工业出版社,2015:51-54.LI Z F.Handbook of wind tunnel test[M].Beijing:The Aviation Industry Press,2015:51-54(in Chinese).

[36] TAM C K W,BLOCK P J W.On the tones and pressure oscillations induced by flow over rectangular cavities[J].Journal of Fluid Mechanics,1978,89(2):373-399.

[37] RONA A.The acoustic resonance of rectangular and cylindrical cavities:AIAA-2007-3420[R].Reston:AIAA,2007.

[38] LARCHEVEQUE L,SAGAUT P,MARY I,et al.Large-eddy simulation of a compressible flow past a deep cavity[J].Physics of Fluids,2003,15(1):193-210.

Test on interactions between aeroacoustic noise and structural vibration in elastic cavity flow

WANG Xiansheng1,2,*,YANG Dangguo1,2,LlU Jun1,2,SHl Ao2,ZHOU Fangqi2,LYU Binbin2

1.State Key Laboratory of Aerodynamics,China Aerodynamics Research and Development Center,Mianyang 621000,China
2.High Speed Aerodynamics lnstitute,China Aerodynamics Research and Development Center,Mianyang 621000,China

Coupling between aeroacoustic noise loads and structural vibration in cavity flow-induced oscillation may bring about severe damage to aircraft,especially when structural resonance occurs.To study the coupling mechanism,elastic cavity tests are performed in a high-speed wind tunnel with 0.6 m×0.6 m cross-section.The natural frequency of the elastic cavity structure can be adjusted by changing the thickness of its floor.Noise and vibration transducers are employed in the tests to obtain acoustic noise loads and structural vibrations.The Mach number ranges from 0.6 to 1.2.lt is shown that under the current conditions,structural vibration has little effect on cavity noise,while cavity noise has an important influence on structural vibration.At the main frequency position of cavity noise,power spectral density of structural vibration peaks and correlation of noise/vibration are the strongest.ln addition,structural vibration is also closely related to the natural frequency of the cavity,and vibration is dominated by the low-order mode.

elastic cavity;flow-induced noise;aeroacoustics;structural vibration;wind tunnel test

2016-10-20;Revised:2016-11-04;Accepted:2017-02-07;Published online:2017-02-17 13:22

URL:www.cnki.net/kcms/detail/11.1929.V.20170217.1322.004.html

s:National Natural Science Foundation of China(11602287,11402286)

V211.7

A

1000-6893(2017)07-120873-10

10.7527/S1000-6893.2017.120873

2016-10-20;退修日期:2016-11-04;录用日期:2017-02-07;网络出版时间:2017-02-17 13:22

www.cnki.net/kcms/detail/11.1929.V.20170217.1322.004.html

国家自然科学基金(11602287,11402286)

*通讯作者.E-mail:xishw@hotmail.com

王显圣,杨党国,刘俊,等.弹性空腔流致噪声/结构振动特性试验[J].航空学报,2017,38(7):120873.WANG X S,YANG D G,LlU J,et al.Test on interactions between aeroacoustic noise and structural vibration in elastic cavity flow[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):120873.

(责任编辑:张晗)

*Corresponding author.E-mail:xishw@hotmail.com