再入飞行器离轨制动在线规划方法

2017-11-21史树峰赵育善

航天控制 2017年5期

关键词：冲量飞行器轨迹

史树峰师鹏赵育善

北京航空航天大学，北京100191

再入飞行器离轨制动在线规划方法

史树峰师鹏赵育善

北京航空航天大学，北京100191

研究了再入飞行器离轨阶段的轨道规划方法。基于轨道飞行原理，建立了冲量模型下离轨制动参数和再入点参数的关系，分析了最优离轨的推力施加原则。在考虑地球自转的前提下，针对约束再入点特定经纬度的问题，利用非线性规划的优化方法，研究了有限推力模型下离轨点位置的确定策略，同时给出了符合燃料最优目标的离轨制动参数。

再入飞行器；最优离轨；有限推力；非线性规划

随着宇航技术的发展以及全球打击作战需求的出现，天基全球攻击作战方案受到了世界强国的普遍重视。此类研究一般以轨道或亚轨道高度再入大气层，如美国提出的通用航空飞行器(CAV)概念就具有出色的作战优势。CAV在待命状态下由运行于400～500km高度潜伏轨道的平台携带，接到攻击命令后，平台释放CAV，CAV依靠离轨模块的制动推力进入飞向地球的下降轨道[1-3]。

为使再入飞行器具备全球定位打击能力，必须研究其在线离轨规划方法。再入飞行器离轨过渡轨道的相关研究中，陈洪波等分析了离轨推力控制与相应的下降轨道再入角之间的关系[4]。高浩等以最短拦截时间为要求，提出了离轨过渡轨道的优化算法[5]。

本文将再入飞行器的定点打击作为研究目标，以再入飞行器从潜伏轨道转移到距地面120km高度的再入点之间的离轨段和过渡段轨道为研究对象，对再入飞行器定点打击的离轨制动时机和离轨控制参数进行了研究。首先分析了再入飞行器离轨任务特性，然后针对圆轨道潜伏轨道推导了冲量变轨模式下的最优离轨轨道，继而提出了有限推力变轨模式下最优离轨关键参数的确定方法，最后通过模拟仿真验证了方法的有效性。

1 再入飞行器离轨制动过程

再入飞行器的返回轨道是指飞行器返回地球并着陆到地球表面过程中质心的运动轨迹。返回轨道可分成4段： 1)离轨段轨道； 2)过渡段轨道； 3)再入段轨道； 4)着陆段轨道[6]。

图1为再入飞行器的离轨再入过程。假设飞行器在原轨道ε1上以速度v1飞行。离轨模块作用在离轨点D并施以制动速度Δv，使飞行器的速度变为v2，从原来的轨道进入到一条与地球大气相交的椭圆过渡段轨道ε2上，并于120km高度处的再入点E开始以速度ve和再入角ϑe进入稠密大气层。本文研究的对象就是从D点到E点的离轨段(有制动推力)和过渡段(无动力滑行)轨道，E点之后的再入段和着陆段轨道不在讨论之列。

图1 离轨再入过程示意图

图1中的离轨段和过渡段轨道，在给定δD和已知v1及ϑ1，也即给定再入飞行器的离轨点D的位置时，离轨点D到再入点E之间的航程角δb的大小由过渡轨道ε2的轨道要素决定。过渡段轨道ε2可由D点的位置、离轨速度v2求得。再入点E就是ε2与大气层上界的相交点。飞行器再入点的状况，即再入点E的位置、再入速度ve和再入角(弹道倾角)ϑe，对飞行器能否成功返回有决定性的影响[7]。

一般认为从D点到E点间的轨道是无大气阻力的空间轨道，E点之后的轨道是受大气影响的气动轨道。再入点E处的再入弹道倾角ϑe和再入对地速度ve会因气动飞行的需要而有特定约束。因此，再入飞行器离轨制动规划的任务可以描述成：根据飞行器当前飞行参数，选择合适的制动发动机点火时机和制动推力参数，使飞行器经过过渡段轨道到达指定的再入点经纬度，并满足任务要求的再入点速度参数，且制动过程具有燃料最优的性能指标。

实际上，从离轨点开始到完成离轨进入过渡段轨道不是在一个点瞬时完成的，制动发动机获得制动速度Δv需要一定的工作时间。本文将先用冲量模型对离轨制动过程进行分析，然后用有限推力模型进行实际规划。

2 圆轨道最优冲量离轨

由于变轨道面机动所耗燃料超出一般离轨制动任务所限，本文离轨制动过程限定在原轨道面内完成。

圆轨道潜伏轨道制动的制动点与再入点关系如图2所示，假设原运行轨道为圆轨道，v1的方向即为当地水平方向。φz为Δv与当地水平的夹角，图中φz为负。同时定义χ=π+φz，图中为正值。v1，ϑ1和r1分别为制动点原轨道速度大小、方向和地心距，v2，ϑ2和r2分别为制动后轨道速度大小、方向和地心距，ve，ϑe和re分别为再入点速度大小、方向和地心距，根据冲量假设，r1=r2。

图2 圆轨道制动的制动点与再入点关系

由轨道力学可知

(1)

r2v2cosϑ2=revecosϑe

(2)

其中，μ为地心引力常数，由图2中三角关系可知

v2cosϑ2=v1-Δvcosχ

(3)

(4)

由式(1)知

(5)

其中，

(6)

将式(3)代入式(2)得

(7)

将式(7)和(4)代入式(5)得

(8)

令

(9)

则式(8)可写成

(10)

对于圆轨道再入问题，因为再入点的地心距re和制动点的地心距r1=r2已知，即α为常数。可以看出，当给定一个χ角，一定可以找出一个Δv，使ϑe满足要求，因此可以找到一个最佳制动角χ0，使Δv即燃料消耗最小，制动发动机工作时间最短。

为此，将式(10)对χ角求偏导得到

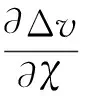
出现驻点的条件

(11)

上式中2个方程分别对应一个最优值

(12)

其中，χ02的成立须满足如下条件

(13)

当制动过程满足方程式(13)时，χ02能使Δv为极值且为极小值；当不满足方程式(13)时，应取χ01为制动方向，使Δv为极值且为极小值，而且此时

(14)

由于一般制动高度h0>300km，而且|ϑe|≤5°，不满足式(13)条件，因此最佳χ0=0，且制动高度越高，Δvmin越大。所以在一般情况下，圆轨道制动方向以反向制动最佳。

由于再入段飞行状态主要受再入弹道倾角影响，因此以上理论是在ϑe确定而对ve的大小不作要求时的讨论，当任务对ve也确定的情况下，χ值对于给定离轨点有确定值。

3 有限推力离轨策略

作为返回任务的基础，首先要确定合适的离轨点。再入飞行器的飞行轨道是确定的，任务下达时间是任意的，因此当接收到返回指令时，飞行器可能处于空间中的任意位置；而返回目标(这里指再入点位置)是基于经纬度描述的相对地面固定位置(如图3)，但在惯性系下是随时间变化的，假设离轨时刻目标位置在P点，实际设计的轨道需要考虑到地球自转因素而确定为P′点。因此在离轨点确定时，研究再入点惯性空间位置会使问题复杂化，考虑将轨道星下点作为主要参考对象。

图3 离轨点选择与目标位置的关系

再入飞行器过渡轨道的参数，完全由制动结束时的运动参数确定。当以轨道星下点为研究对象时，由于从离轨制动到进入再入点的过程不超过半个轨道周期，而且轨道形状改变程度也不大，所以离轨后的星下点轨迹接近于原轨道星下点轨迹。因此标准过渡轨道应满足如下要求：

1)离轨点在原轨道上，其轨道星下点轨迹应通过再入点地理经纬度；

2)再入点倾角ϑe和再入速度ve应满足任务要求。

为满足这2点要求，可供调整的参数有制动点位置，即制动点的经纬度，但为了保证制动点位置在原轨道上，实际可控参数只有经度或纬度；另一可调整参数是发动机推力大小、方向和工作时间。

上节确定制动发动机推力方向的方法以瞬时冲量模型为基础，而在实际情况下，发动机推力为有限值，速度增量并非冲量，为此需要使用非线性规划方法确定离轨任务的各关键参数。

有限推力下的离轨动力学模型为

(15)

其中，μ为引力常数，T为发动机推力，m为飞行器质量，ap为需要考虑的摄动力，g0为海平面处重力加速度，Isp为发动机比冲。

在有限推力模式下，当推力的大小给定时，需要确定的是制动发动机推力的方向和工作时间。具体算法是以冲量法的制动角χ为基础制动方向，通过计算得到满足再入角要求的制动发动机工作时间t，再通过非线性规划方法找出符合再入速度要求的最佳制动方向。这样再入点的速度参数得到了满足，但再入点位置并不满足任务要求，须要在原轨道的星下点轨迹上搜索找出能准确到达再入点位置的制动起始位置。另外，为了保证离轨任务的精度，参数确定过程中需要考虑必要的摄动因素，由于离轨过程时间较短且在低轨道高度进行，所以本文主要引入了J2摄动项。

离轨制动点具体规划策略如下：

第1步：选定制动点位置(B0,λ0)，用迭代方法求满足ϑe和ve的制动发动机方向和工作时间tp。具体步骤为：

1)初选制动点(B0,λ0)：在星下点轨迹过再入点的运行轨道上(原轨道的第N圈)，选一制动点经度λ0，根据第N圈星下点轨迹的数据求出与λ0对应的大地纬度B0；

2)求制动点(B0,λ0)相对应的制动发动机参数：由冲量模型计算制动点的初始推力方向，通过非线性规划方法得到再入高度120km处满足再入角要求的制动发动机工作时间。

第1步规划实际上是带约束的非线性规划问题，其数学描述如下

(16)

其中，等式约束为规划结果的再入点倾角须满足任务要求。离轨制动规划使用SNOPT非线性规划方法[8]，并以第2节中冲量模型的计算结果作为规划初值。

图4 离轨制动参数规划流程

第2步：对于第1步选定的制动点(B0,λ0)和制动点参数，计算再入点位置误差Δe，迭代修正再入点位置，直到满足任务要求。

第2步规划实际上是在原轨道上对制动点的一维搜索，搜索方法选择使用牛顿法。

第1、2步是不断重复的过程，每一次由Δe修正(B0,λ0)时，也要重复第1步对发动机参数进行修正，流程如图4所示。

4 离轨制动规划仿真

根据前文介绍的方法，对离轨制动的具体任务进行模拟仿真。再入飞行器及发动机参数如表1所示。

表1 再入飞行器参数

初始轨道为高度400km的圆轨道，初始历元为UTC 2016/10/1 20:00:00。其轨道根数如表2所示。

表2 初始轨道根数

再入点速度参数要求弹道倾角为-1.235°。

仿真中选取了3个不同纬度的目标再入点位置，满足处于原轨道星下点轨迹上的要求，且处于星下点轨迹的不同轨道号上，如表3所示。

表3 再入点经纬度

图5 飞行器原轨道的星下点轨迹

为了选择离轨制动点火时机，首先要对原始轨道星下点轨迹进行预报，如图5所示，根据任务所给轨道参数，用12阶地球引力场模型对飞行器初始轨道进行了24h预报，并计算其相应的星下点轨迹。以1号计算目标为例，实心圆点代表飞行器初始位置，箭头指示飞行方向，空心方块代表任务指定的再入点星下点位置，虚线代表5°纬度线。再入点位置恰好处于再入飞行器原轨道星下点轨迹上，而且是星下点轨迹西南-东北向与纬度线相交的位置。再入点位于飞行器初始历元之后1周期左右的星下点轨道上，因此可以将方形代表位置的半周期之前的轨道位置作为离轨点规划的初始选择范围。

仿真中使用了SNOPT非线性规划方法，对于任意选定的离轨点位置，都能计算出最优燃耗且满足弹道倾角的推力方向和持续时间，这样计算得到的再入点只符合高度约束，不满足经纬度约束。通过迭代调整离轨点，将再入点适配到目标位置上。实际结果如图6，虚线表示原轨道第2圈的星下点轨迹，实线表示离轨段和过渡段轨道的星下点轨迹；实心圆点代表计算得到的离轨点星下点位置(11.3896°，-32.5323°)，星形表示离轨制动推力结束，自由下降段开始的位置，空心方形为任务要求的再入点位置，箭头表示星下点轨迹方向。由图可见，通过仿真得到的再入点位置符合任务要求(经纬度误差在0.01°量级)。在普通计算机上以Matlab平台进行仿真，耗时10s左右，程序优化后应能作为线上计算工具。类似得到其他2组仿真，由于离轨任务相似，制动过程参数相差不大，主要差别为离轨时刻，具体的离轨点参数如表4。

表4 离轨制动参数规划结果

图6 离轨过程的星下点轨迹

通过仿真得知，当飞行器轨迹过再入点星下点时，可以通过有限推力的优化计算得到关于离轨点的一系列参数。而当飞行器星下点轨迹远离再入点时，需要预先通过轨道机动调整轨道，将轨道星下点调整到过再入点的状态，再利用本文的方法进行规划计算。

5 结论

研究分析了指定再入点飞行任务中，再入飞行器在线规划离轨制动参数的方法。

首先根据飞行器当前轨道参数和目标再入点参数，利用冲量模型计算离轨参数初值；进而使用有限推力假设计算燃料最优的实际推力方向和推力时间，并利用非线性规划方法确定离轨制动的点火时机。本文方法对于约束飞行器再入点经纬度的一类问题有良好的规划结果，对其他关于再入飞行器离轨制动段的研究具有参考价值。

[1] Richie G. The Common Aero Vehicle: Space Delivery System of the Future[C]. AIAA Space Technology Conference and Exposition. Albuquerque, 1999.1-11.

[2] Pournelle P T. Component Based Simulation of the Space Operations Vehicle and the Common Aero Vehicle[D]. Naval Postgraduate School, United States Navy,Monterey,CA,1999:3-10.

[3] 南英,陈士橹,吕学富，等. 航天器再入轨迹与控制进展[J]. 导弹与航天运载技术, 1994, (5):1-11.(Nan Ying, Chen Shilu, Lv Xuefu, et al. The Progress of Reentry Trajectory and Control of Space Vehicle[J]. Missiles and Space Vehicles, 1994, (5):1-11.)

[4] 陈洪波, 杨涤. 升力式再入飞行器离轨制动研究[J]. 飞行力学, 2006, 24(2): 35-39. (Chen Hongbo, Yang Di. Deorbit Operations Study of Lifting Reentry Vehicle[J]. Flight Dynamics, 2006, 24(2): 35-39.)

[5] 高浩, 张科, 王佩. 天基拦截器过渡轨道优化研究[J]. 飞行力学, 2014, 32(2):155-159. (Gao Hao, Zhang Ke, Wang Pei. Transitional Orbit Optimization Research of Space-Based Interceptor [J]. Flight Dynamics, 2014, 32(2): 155-159.)

[6] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997:289-299. (Zhao Hanyuan. Reentry Dynamics and Guidance of Space Vehicle[M]. Changsha:National NUDT Publish House, 1997:289-299.)

[7] 王希季. 航天器进入与返回技术[M]. 北京: 宇航出版社, 1991. (Wang Xiji. Spacecraft Entry and Return Technology[M]. Beijing: China Astronautic Publishing House, 1991:115-120.)

[8] 袁方. 最优过程理论在飞行轨迹优化计算中的应用[J]. 飞行力学, 2000, 18(1): 50-53. (Yuan Fang. The Application of Optimum Process Theory in Calculation of Optimal Trajectory for Flight[J]. Flight Dynamics, 2000, 18(1): 50-53.

TheOn-LinePlanningMethodforDeorbitProblemofReentryVehicles

Shi Shufeng ， Shi Peng， Zhao Yushan

Beijing University of Aeronautics and Astronautics, Beijing 100191, China

Thetrajectoryon-lineplanningofreentryvehiclesisconstrainedbytheparametersofthereal-timeorbitandtheaimingreentrypoint.Thedeorbitcontrolparametersdeterminethetransitionorbitandinturndominatetheconditionandprecisionofthereentrypoint.Basedontheprinciplesoforbitalflight,therelationshipbetweendeorbitparametersandreentrypointparametersisestablishedwiththeimpulsethrustmodel.Thenthemethodoftheoptimalthrustdirectiondeterminationisdeveloped.Byconsideringtheinfluenceofearthrotationandfinitethrust,thestrategyofsearchingtheoptimaldeorbitfireoccasionisresearchedwiththenonlinearprogrammingmethod.Andthedeorbitcontrolparametersaredeterminedasaresultofthisapproach.

Reentryvehicle;Optimaldeorbit;Finitethrust;Nonlinearprogramming