带挠性附件航天器在轨质量特性辨识

王首喆 张庆展 靳永强 盛英华

上海宇航系统工程研究所，上海 201109

带挠性附件航天器在轨质量特性辨识

王首喆 张庆展 靳永强 盛英华

上海宇航系统工程研究所，上海 201109

考虑挠性附件的振动，研究了航天器在轨质量特性辨识问题。利用推力器产生激励，采用陀螺仪、加速度计和振动信号传感器作为敏感器，设计了模态滤波器提取各阶模态响应。通过交互迭代，设计了转动惯量和质心位置的辨识算法；根据加速度计原理，设计了质量的辨识算法。采用批量最小二乘法对算法进行求解。该算法适用于模态参数已知、任意初始状态航天器的质量特性辨识。仿真结果表明算法收敛速度快、辨识精度高。

质量特性；挠性附件；交互迭代；模态滤波器；最小二乘法

随着航天技术的发展，空间任务由简单变得复杂。航天器需要通过高精度轨道和姿态控制来实现航天器及有效载荷的高精度指向[1]。准确已知航天器的质量特性参数(转动惯量、质心位置和质量)对航天器的高精度控制有很大影响。由于以下原因，使得航天器的质量特性参数发生变化： 1)长期在轨运行引起的推进剂消耗；2)航天器在轨组装构成组合体； 3)航天器在轨燃料加注； 4)有效载荷正常工作导致惯性参数变化； 5)航天器结构发生故障或损毁等。同时，太阳帆板、天线等部件使得航天器结构变得复杂，刚体模型不再适用，需要研究带挠性附件航天器的在轨质量特性参数辨识方法。

文献[2]提出一种针对自旋卫星的最小二乘辨识算法；文献[3]利用速率陀螺的测量数据，通过基于指数加权递归最小二乘算法，对转动惯量和质心位置进行辨识；文献[4]利用重力梯度力矩对飞行器转动惯量进行辨识；文献[5]将参数辨识问题转换为非线性系统的全局优化问题，提出基于粒子群(PSO)的非线性优化算法辨识出所有的参数；文献[6]利用飞轮作为执行机构，分别提出了一种基于递推最小二乘法的航天器转动惯量在线开环辨识和闭环辨识算法；文献[7]用陀螺测得的角速度、推力标称值和推力作用点的位置信息构造量测，采用最小二乘法对转动惯量进行估计。上述文献均是在刚体模型的基础上，对单个航天器进行质量特性辨识。文献[8]针对捕获非合作目标的航天器，依据动量矩定理建立组合系统动力学模型，采用非线性规划方法对质量特性进行辨识；文献[9]利用条件数和奇异值分解理论对航天器质量特性参数的可辨识性及可辨识度进行了分析，并提出辨识策略和算法；文献[10]通过设计合适的推力器工作策略，提出一种闭环稳定的解耦质量特性辨识方法。上述文献的研究对象均是航天器与合作或非合作目标构成的组合体。文献[11]研究了单臂自由飘浮空间机器人抓取未知目标的质量特性参数表示问题；文献[12]根据多体动力学方程，采用递推最小二乘法对捕获的空间非合作目标质量特性进行估计；文献[13]采用PSO算法对一类多自由度空间机器人卫星的惯性参数进行了在轨辨识。上述文献研究对象均为多体动力学模型。文献[14]对空间绳系机器人抓捕的非合作目标的质量特性进行辨识。

综上，目前对航天器质量特性辨识的研究主要以刚体模型为主，对带有挠性附件的对象研究较少。本文以陀螺与加速度计为敏感器，分别测量航天器角速度和非保守力加速度，利用挠性附件表面用于振动主动控制而安装的振动信号传感器获得挠性附件的振动信息，对带有挠性附件航天器的质量特性参数在轨辨识算法进行了研究。

1 在轨辨识算法

1.1 动力学模型

对坐标系进行定义：1)J2000惯性坐标系Oixiyizi；2)航天器本体坐标系Obxbybzb； 3)第j个挠性附件的挠性附件坐标系Ojxjyjzj：原点Oj取挠性附件与航天器的联接点，为了计算方便，假设Ojxjyjzj各轴与Obxbybzb各轴平行；4)布局坐标系Oexeyeze：原点Oe位于航天器与火箭末子级连接环的中心，各轴与Obxbybzb各轴平行。

带挠性附件航天器动力学模型：

(1)

(2)

(3)

式中，r为航天器的位置矢量，ω为航天器的转动角速度，m为航天器质量，J为未变形航天器转动惯量矩阵，Btranj为第j个挠性附件的平动耦合系数，Brotj为第j个挠性附件对于本体坐标系Obxbybzb的转动耦合系数，ηj为第j个挠性附件的模态坐标，Λj，ζj分别为第j个挠性附件的模态频率矩模态阻尼比矩阵，Fi，ri为第i个推力器的推力与安装位置，Fd，Td为航天器受到的干扰力与干扰力矩，a为航天器线加速度，rcm为航天器质心相对Oexeyeze原点Oe的位置矢量。

(4)

(5)

1.2 质心坐标计算方法

由于环境干扰力、干扰力矩相比控制力、控制力矩小得多，所以在辨识过程中可以忽略不计。将式(5)代入(2)得：

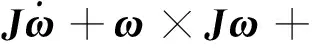
(6)

其中，Fi，ri在辨识过程中视为已知量。

对式(6)中含有质心坐标rcm的各项进行整理有

(7)

(8)

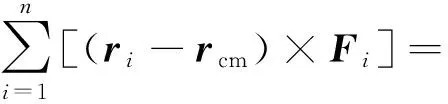
(9)

将式(7)～(9)带入式(6)，将含有质心坐标rcm的各项移至等号左边，其余项移至等号右边，整理得

(10)

将式(10)表示为Acxc=bc的形式，其中：

将陀螺仪测得的角速度信息ω带入上式，从而实现对质心坐标的辨识。

1.3 转动惯量矩阵计算方法

AJ=A1+A2

(11)

式中，A1和A2表达式分别为

将式(6)整理为AJxJ=bJ的形式，bJ表达式为

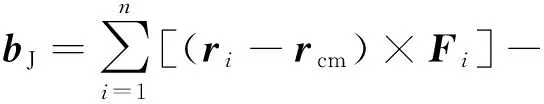
(12)

1.4 质量计算方法

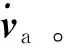
(13)

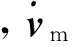
1.5 模态滤波器设计

上述辨识过程中，涉及到挠性附件振动的模态值，需要从结构振动中准确地提取独立的各阶模态响应。通常，为了对挠性附件进行抑振控制，挠性附件表面的几处应变最大区域安装有振动信号测量传感器，可利用这些传感器测得对应位置的物理振动量。因为挠性附件振动是各阶模态的相互叠加，需对传感器输出的振动信号进行模态分离，提取出各阶模态量[15]，本文引入模态滤波器实现从物理振动量得到模态量。

挠性附件的振型、频率可通过有限元软件分析得到。假设第j个挠性附件经有限元分析求得相对Ojxjyjzj系的阵型矩阵为

Φj=[φj1,φj2,…,φjN]

式中，N为振型的截断数。

1.6 质量特性计算方法

采用基于交互式迭代和批量最小二乘的计算方法对质量特性参数进行求解，流程如图1所示，迭代次数为n次，k为当前迭代次数。每一步计算均采用多元线性批量最小二乘回归算法，假设采样了M组数据，可以组成如下方程组：

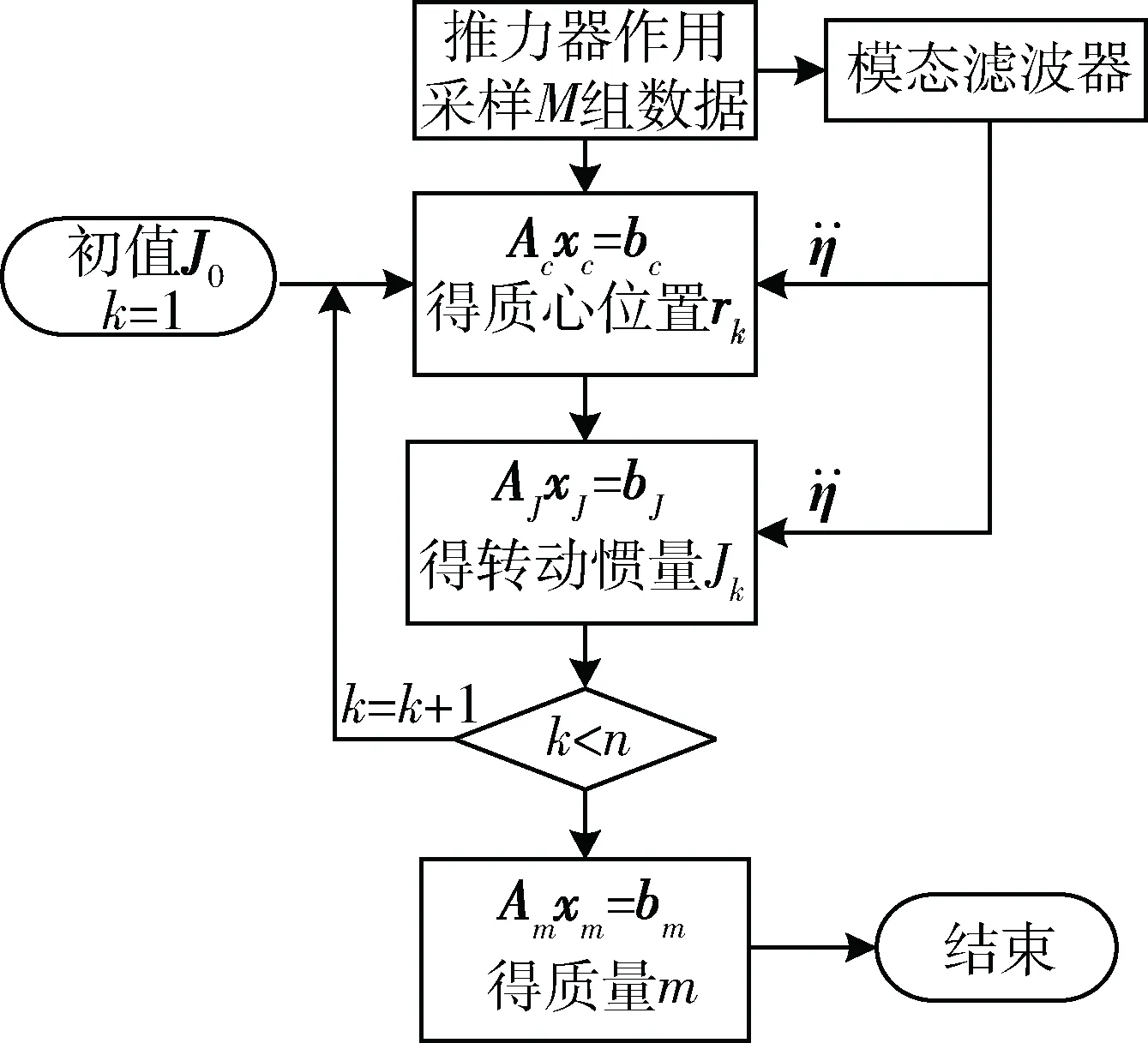
图1 质量特性参数辨识流程图

方程的最小二乘解为

x=(LTL)-1LTb

(14)

2 仿真

通过数学仿真，对所提的辨识算法进行验证。航天器质量特性参数的标称值为：

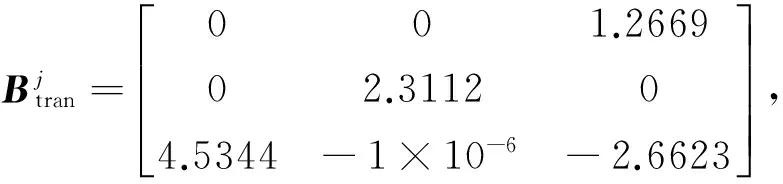
表1 推力器安装位置及推力方向

仿真中，考虑陀螺仪常值漂移为3.5(°)/h，随即游走系数为0.025(°)/h，马尔科夫相关时间常数为3000s，驱动噪声均方值为0.15(°)/h。考虑加速度计常值漂移为1×10-4m/s2，随即游走系数为5×10-5m/s2，马尔科夫相关时间常数为1800s，驱动噪声均方值为1×10-5m/s2。实际推力器推力考虑5%的误差，挠性附件振动响应考虑5%的测量误差。

图2为转动惯量的辨识结果，其中图(a)～(c)为主惯量值的辨识结果，辨识精度分别为0.74%，0.45%，0.55%；图(d)～(f)为惯量积的辨识结果，辨识结果与标称值的数量级相当。由于惯量积与主惯量是同时辨识的，而惯量积比主惯量小得多，因此在绝对误差值相当的情况下，主惯量的辨识精度比惯量积的辨识精度要高。图3为航天器惯量积标称值J12=-800kg·m2，J13=-700kg·m2，J23=-760kg·m2时的辨识结果，辨识精度分别为1.43%，1.61%，2.22%。可以看出，随着惯量积的增大，辨识精度相应地提高。当惯量积的值较小时，对航天

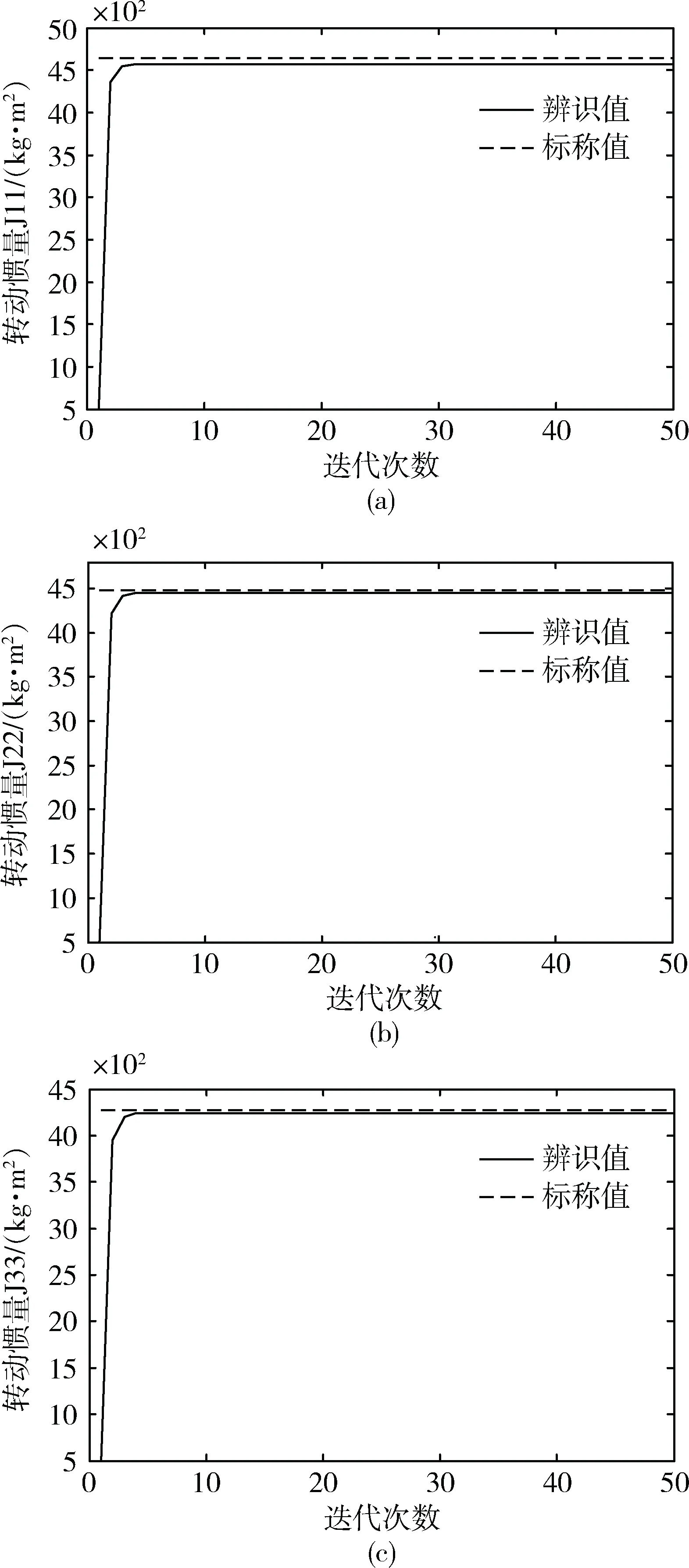
图2 转动惯量辨识结果

图3 惯量积(数值较大)辨识结果

图4 质心位置辨识结果

器控制的影响不大；当惯量积的值较大时，本文算法的辨识精度能够满足控制的要求，该算法对转动惯量的辨识结果是有效的。图4为质心位置的辨识结果，质心三轴坐标值的辨识精度分别为0.23%，0.35%，0.33%。质量的辨识结果为3481.9kg，辨识精度为0.52%。

3 结论

根据带有挠性附件航天器的动力学模型，分别设计了转动惯量、质心位置、质量的辨识算法。该算法基于推力器对航天器施加激励，通过陀螺仪、加速度计和振动信号传感器获得航天器的角速度、非保守力加速度和挠性附件振动响应，从而对航天器质量特性参数进行辨识。对算法进行了仿真验证，结果表明所设计的辨识算法准确有效，可为航天器在轨精确控制提供参考。

[1] 张洪波, 武向军, 刘天雄, 等. 一种在轨卫星质量特性计算方法[J]. 航天器工程, 2013, 22(6): 30-36.(Zhang Hongbo, Wu Xiangjun, Liu Tianxiong, et al. A Method of Mass Property Calculation for On-orbit Satellites[J]. Spacecraft Engineering, 2013, 22(6): 30-36.)

[2] Tanygin S, Williams T. Mass Property Estimation Using Coasting Aneuvers[J]. Journal of Guidance, Control, and Dynamics， 1997, 20(4): 625-632.

[3] Wilson E, Lages C, Mah R. On-line, Gyro-based, Mass-property Identification for Thruster-Controlled Spacecraft Using Recursive Least Squares[C]. The 45thMidwest Symposium on Circuits and Systems, Tulsa, Oklahoma, Aug. 4-7, 2002.

[4] Yosida K, Abiko S. Inertia Parameter Identification for a Free-Flying Space Robot[J], Transactions of the Japan Society of Mechanical Engineers C, 2002, 68(672):AIAA 2002-4568.

[5] 徐文福, 何勇, 王学谦. 航天器质量特性参数的在轨辨识方法[J]. 宇航学报, 2010,31(8):1906-1914.(Xu Wenfu, He Yong, Wang Xueqian. On Orbit Identification of Mass Characteristiec Parameters for Spacecraft[J]. Journal of Astronautics, 2010,31(8):1906-1914.)

[6] 黄河, 周军, 刘莹莹. 航天器转动惯量在线辨识[J]. 系统仿真学报, 2010,22(5):1117-1120.(Huang He, Zhou Jun, Liu Yingying. On-orbit Identification of Spacecraft Moment of Inertia[J]. Journal of System Simulation, 2010,22(5):1117-1120.)[7] 李广兴, 肖余之. 某大结构变化空间飞行器转动惯量在轨估计[J]. 上海航天, 2011,(28):22-26.(Li Guangxing, Xiao Yuzhi. Estimation On-line for Inertia Tensor of Space Vehicle with Large Structural Change[J]. Aerospace Shanghai, 2011,(28):22-26.)

[8] 韦文书, 荆武兴, 高长生. 捕获非合作目标后航天器的自主稳定技术研究[J]. 航空学报, 2013,34(7):1520-1530.(Wei Wenshu, Jing Wuxing, Gao Changsheng. Research Automatic Stability Technology of Spacecraft Assembly with Captured Non-cooprative[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(7):1520-1530.)

[9] 荆武兴, 韦文书, 高长生. 基于陀螺测量信息的航天器突变参数辨别方法[J]. 系统工程与电子技术, 2013,35(9):1928-1932.(Jing Wuxing, Wei Wenshu, Gao Changsheng. Identification of the Mutation Parameters for the Spacecraft Based on Gyros[J]. Systems Engineering and Electronics, 2013,35(9):1928-1932.)

[10] 侯振东, 王兆魁, 张育林. 基于推力器的组合航天器质量特性辨识方法研究[J]. 航天控制, 2015,33(1):54-60.(Hou Zhendong, Wang Zhaokui, Zhang Yulin. Research on Identification of Mass Characteristics for Spacecraft Combination Based on Thrusters[J]. Aerospace Control, 2015,33(1):54-60.)

[11] 金磊, 徐世杰. 空间机器人抓取未知目标的质量特性参数辨识[J]. 宇航学报,2012,33(11):1570-1576.(Jin Lei, Xu Shijie. Inertial Parameter Identification of Unknown Object Captured by a Space Robot[J]. Journal of Astronautics, 2012,33(11):1570-1576.)

[12] 张海博, 王大轶, 魏春岭. 空间非合作目标质量特性在轨辨识[J]. 航天控制, 2015,33(3):23-28.(Zhang Haibo, Wang Dayi, Wei Chunling. On-orbit Identification of Mass Properties of Non-Cooperative Space Target[J]. Aerospace Control, 2015,33(3):23-28.)

[13] 马欢, 李文皓, 肖歆昕, 等. 空间机器人惯性参数辨识的粒子群优化新算法[J]. 宇航学报, 2015,36(3):278-283.(Ma Huan, Li Wenhao, Xiao Xinxin, et al. A New Particle Swarm Optimization Approach to the Inertia Parameters Identification of on Orbit Space Robot[J]. Journal of Astronautics, 2015,36(3):278-283.)

[14] 张帆, 黄攀峰. 空间绳系机器人抓捕非合作目标的质量特性参数辨识[J]. 宇航学报, 2015,36(6):630-639.(Zhang Fan, Huang Panfeng. Inertial Parameter Estimation for an Noncooperative Target Captured by a Space Tethered System[J]. Journal of Astronautics, 2015,36(6):630-639.)

[15] 吴大方, 黄良, 潘兵, 等. 大柔性压电梁振动主动控制实验研究与数值模拟[J]. 强度与环境, 2012(5):7-17.(Wu Dafang, Huang Liang, Pan Bing, et al. Experimental Study and Numerical Simulation of Active Vibration Control of a Highly Flexible Beam Using Piezoelectric Intelligent Material[J]. Structure and Environment Engineering, 2012(5):7-17.)

[16] 卢连城, 吴琼, 张令弥. 智能空间桁架结构独立模态控制方法[J]. 振动工程学报, 1997,10(4):480-485.(Lu Liancheng, Wu Qiong, Zhang Lingmi. Modal Filter Control Method for Intelligent Space Truss Structures[J]. Journal of Vibration Engineering, 1997,10(4):480-485.)

IdentificationofMassPropertyforOn-OrbitSpacecraftswithFlexibleAppendages

Wang Shouzhe, Zhang Qingzhan, Jin Yongqiang, Sheng Yinghua

Aerospace System Engineering Shanghai, Shanghai 201109, China

Byconsideringflexiblevibration,astudyonidentificationofmasspropertyforspacecraftsisimplemented.Byactuatingthrusters,informationisobtainedbyusinggyro,accelerometerandvibrationsignalsensor,thenmodalresponseisacquiredbyapplyingmodalfilter,andinertiatensorandcenterofmasspositionarecalculatedbyinteractiveiteration,andthetotalmassiscalculatedbyaccelerometer’sprinciple.Thisalgorithm’snumericalsolutionissolvedbybatchleastsquare.Thealgorithmissuitableforspacecraftswhosemodeparametersareknownandinitialstatesarerandom.Thesimulationresultsindicatethatthisalgorithmcanconvergesrapidlyandhashighidentificationprecision.

Massproperty;Flexibleappendage;Interactiveiteration;Modalfilter;Leastsquare

V448.2

A

1006-3242(2017)05-0009-06

2016-09-08

王首喆(1992-)，男，山西人，硕士研究生，主要研究方向为飞行器总体设计；张庆展(1987-)，男，山东人，硕士，工程师，主要研究方向为飞行器制导、导航与控制；靳永强(1981-)，男，山西人，博士，研究员，主要研究方向为飞行器总体设计；盛英华(1977-)，男，黑龙江人，硕士，研究员，主要研究方向为运载火箭总体设计。