仿真转台若干性能问题讨论

张新邦 曾海波 张锦江 朱志斌

北京控制工程研究所，北京 100190

仿真转台若干性能问题讨论

张新邦 曾海波 张锦江 朱志斌

北京控制工程研究所，北京 100190

仿真转台低速性能的控制技术方面已有一些研究，但是对低速性能的描述、测试、判断等方面的讨论很少。本文提出可以应用“最低平稳速度”和“低速位置控制精度”来量化描述低速性能。在测试转台的动态性能时，除了频率响应法，可应用快速停止法作进一步测试。应用多信号输入(将位置、速度及加速度信号同时输入到转台控制系统)和适当的前馈方法可提高转台的动态响应性能。应用多输入复合控制方法将进一步提高系统的动态响应性能。

仿真转台；低速性能；动态响应

航天器半物理仿真试验对转台性能有很高的要求，既要求低速时速度平稳，又要求在高动态情况下有良好的动态响应。

目前对转台低速性能的控制技术方面已有一些研究[1-2]，但是对低速性能的描述、测试和判断等方面的讨论很少。应该指出传统的速度精度测试在讨论低速性能时是无意义的。文献[3]内关于判断转台低速性能的“误差带法”是个实用的好方法，但缺少深入的讨论。

在高动态性能方面传统的动态响应测试方法有时不能满足要求，应该完善测试方法。同时某些试验对运动模拟器/转台的动态性能提出更高要求，如航天器对接机构的半物理仿真试验中，希望运动模拟器有更好的动态响应[4]。目前的转台是单信号输入系统(输入角位置信号)，以位置反馈控制为主框架，再辅以各种提高动态性能的措施，若要求动态性能再提高一个台阶则无能为力了，所以需要研究新的方法。下面对这些问题分别进行讨论。

1 转台低速性能

1.1 低速爬行现象

先举一个实际例子，上世纪90年代某型号卫星姿态控制系统半物理仿真试验中，转台的低速性能差，表现为低速时速度不平稳，时动时停，称为低速爬行现象。在实测转台的位置控制精度时，如果转台从一个角位置运动到另一个角位置的过程中应用非低速(如1(°)/s)，则位置控制精度为0.001°；而应用低速(如0.001(°)/s)，则位置控制精度为0.005°。在以0.001(°)/s的低速转动时，转台大部分时间处于停止状态，大约每过5s转台一次转动0.005°，匀速运动变成时动时停的台阶状曲线(爬行运动曲线)，台阶宽为5s，高为0.005°。

由于卫星控制系统应用的是速率积分陀螺，所以转台的低速爬行现象没有对半物理仿真试验产生明显不良影响，试验顺利完成，各项指标符合要求，除了卫星姿态稳定度没有满足要求。卫星姿态稳定度应该是0.001(°)/s (3σ)，而半物理仿真试验得到的数据中滚动轴0.0039(°)/s(3σ)，俯仰轴0.0011(°)/s(3σ)，偏航轴0.0036(°)/s(3σ)。这是由于转台的低速性能差，降低了仿真试验的逼真度，影响了试验结果。而其中俯仰轴数据较好，是因为俯仰轴上附加有约0.06(°)/s的轨道角速度，离开了低速爬行区间。

姿态稳定度是卫星控制系统性能的一个重要指标，尤其对于遥感等一类卫星，对姿态稳定度的要求越来越高，所以对转台低速性能问题的讨论是有意义的。

1.2 转速精度

转台转速误差或转速精度的传统测试方法是定时测角法或定角测时法，对于慢速情况一般用定时测角法，转速的相对精度是：

(1)

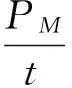
式(1)中，|PS-PM|≤转台的位置控制精度，对于数控的位置转台，位置控制精度是一个定值，而PS是一个变量且随着t的增大而趋无穷大，所以随着时间增加(忽略t的误差)，KV值(速度精度/误差)将趋于无穷小。此方法测得的是平均速度的精度，当转台运行于低速状态出现爬行现象，转速明显处于不平稳状态时，此转速精度是无意义的。

1.3 低速位置控制精度

由上面的例子可知，低速爬行现象使转台的位置控制精度变差，低速位置控制精度是转台在低速状态且出现爬行现象时的位置控制精度，简称低速位置精度。

若无特殊说明，位置控制精度(简称位置精度)是指非低速情况下的位置控制精度。

上面例子中的转台位置精度为0.001°，而低速位置精度为0.005°。其低速爬行曲线为台阶状曲线，爬行幅值(台阶高度)是低速位置精度(0.005°)。可以用低速位置精度量化描述低速爬行现象。

1.4 最低平稳速度

以最低平稳速度为界，当转速小于最低平稳速度，转台将出现爬行现象。当转速不小于最低平稳速度，则转台转动平稳，无爬行现象。

上面仿真试验例子中，由于俯仰轴上附加有约0.06(°)/s的轨道角速度，离开了低速爬行区间，所以转台的最低平稳速度应不大于0.06(°)/s 。

应用“最低平稳速度”、“低速位置精度”和“位置精度”几个变量，基本上可以较完整量化描述转台的低速性能。

1.5 “误差带”描述法

文献[3]内应用“误差带”判断转台低速性能：对于给定的小信号斜坡输入(即给定一个低速直线运动)，要求输出角位置在规定的误差带之间随时间均匀变化，则认为该系统在此低速状态下是平滑的。

这是一个比较实用的方法，但没有进行深入讨论，没有指出如何得到误差带。实际上此误差带值和位置精度有关，一般情况下，误差带区间应不小于位置控制精度。

2 转台动态响应性能

2.1 动态响应测试

传统的动态响应测试方法应用频率响应法，即测量该系统对输入某频率正弦信号的响应，应用输出和输入信号的相移和幅值变化，判断系统动态响应的性能。随着技术的发展和变化，发现此传统方法不够完善：如某转台在测试中相移和幅值变化量都很好，完全满足要求；但在实际使用中动态性能不好。再应用快速停止法测量转台的动态跟踪能力，即转台先处于匀速转动(转速可参考上面频率法测试中系统的最大速度)，再令转台匀减速到停止(匀减速的加速度值可参考频率法测试中系统的最大加速度)，发现输出和输入信号的曲线有较大的误差，输出曲线有一个过冲，表示系统的动态跟踪能力差。

传统的频率响应法经过理论和实践的考验，是可信赖的，但为何出现上面的问题，分析后发现是由于在转台控制中应用了某种前馈控制。

2.2 前馈控制

前馈控制是通过对输入信号的分析处理，预测系统的变化趋势，在此基础上提前采取控制措施，将可能发生的偏差消除在萌芽状态，从而提高了系统的动态跟踪响应能力。而在反馈控制中，只有当输出量受到影响以后控制作用才能开始产生，所以反馈控制特点决定了难以提高动态响应能力。

位置转台的前馈控制技术一般应用将控制量提前的方法，即首先对以前的位置数据进行微分得到速度和加速度，再外推/预估下一个(或多个)步长的位置值，并以此值代替当前数值进行控制，这相当于将输入信号提前了一个(或多个)步长，即动态响应的相移减小了一个(或多个)步长的当量。

由于频率法测试时应用的是正弦信号，可进行无穷多次微分，也可以预估多个步长的位置值并进行控制，大大提高了动态响应性能。但是在实际仿真试验中或应用快速停止法测试时，速度信号往往是不可导的，导致无法正确预测输入信号的变化趋势，使系统实际的动态性能不能满足要求。

2.3 提高动态响应设想

1)多信号输入和前馈

上面讨论的前馈技术本身没有错，只是方法上需要作限制和改进。首先不能预估多个(2个或2个以上)步长的位置值，可以预估1个步长的位置值，并应用多信号输入的方法提高预估精度。

一般转台的输入只有仿真计算机输出的位置(姿态角)信号，所以转台控制系统是单信号输入系统。而对于整个卫星姿态控制仿真系统来说，仿真计算机进行卫星动力学仿真时，卫星姿态角的加速度、速度和位置值都可以得到。可以将位置、速度和加速度等多个信号同时输入到转台控制系统，再用以下公式预测下一步的位置值：

P2=P1+V1Δt+0.5A1(Δt)2

(2)

其中，P1，V1和A1分别为输入的位置、速度和加速度值；Δt为仿真步长；P2为预测下一步的位置值。

此方法在Acutronic公司生产的转台中得到应用[5]，如其产品Three Axis Motion Simulator Series AC3357-140 的控制系统工作模式除了位置(posion)模式、速度(rate)模式之外，还有跟踪(track)模式。跟踪模式用于实时控制运动场合，仿真计算机来的信号可以是长矢量(位置、速度和加速度)，也可以是短矢量(位置和速度)。在应用长矢量时，位置控制信号是长矢量内的位置、速度和加速度数据再应用上面的式(2)而得到。

2)多输入和复合控制

从动态响应实质过程看，当前的加速度信息应该是最重要的，“加速度”比“位置”和“速度”包含有更丰富的动态信息，但这信息没有得到充分有效利用。如需要进一步提高动态响应性能，应以“加速度”作为控制变量实施控制。一般的转台控制系统以位置作为控制变量，系统性能可近似于一个二阶系统，而二阶系统的固有特性使得系统难以进一步提高动态响应的能力。如果以“加速度”作为控制变量实施控制，控制力矩和角加速度之间的关系比较简单，或近似于一个零阶系统，从根本上避开二阶系统这个难题。

综合以上内容后提出多输入复合控制设想：转台控制系统增加对加速度信号的开环控制，这需要转台的数学模型清楚正确。同时转台控制系统对位置信号进行闭环控制。整个系统是加速度开环控制和位置闭环控制的复合控制。当加速度值较小或为0时，位置闭环控制起主要作用，系统保持原来非高动态条件下的各种优点，有满意的性能和精度。当加速度值较大时，加速度开环控制起主要作用使系统得到满意的动态性能，同时位置闭环控制起辅助作用使系统不出现大的漂移。

3 结论

1)传统的速度精度测试在讨论转台低速性能时是无意义的；

2)提出“最低平稳速度”和“低速位置控制精度”的定义，指出爬行曲线幅值(爬行曲线的台阶高度)等于低速位置控制精度，误差带法的误差区间不小于非低速位置控制精度；

3)在测试系统的动态性能时，频率响应法对于应用某种前馈控制可能无法得到正确的结果，此时可应用快速停止法来进一步测试系统的动态性能；

4)应用多信号输入(将位置、速度及加速度信号同时输入到转台控制系统)和适当的前馈控制可提高系统的动态性能。此方法简单易行，可将前馈功能放到仿真计算机内完成，而不必对转台进行任何改动；

5)提出应用多输入复合控制方法：转台控制系统对加速度信号进行开环控制，对位置信号进行闭环控制，整个系统是加速度开馈控制和位置闭馈控制的复合控制，可使系统的动态响应性能再提高一个台阶。

[1] 张锦江，吴宏鑫，李季苏，邹广瑞. 高精度伺服系统低速问题研究[J]. 自动化学报，2005,28(3)：431-434. (Zhang Jinjiang, Wu Hongxin, Li Jisu, Zou Guangrui. Research on Low-speed Problem of High Precision Servo System[J]. Acta Automatica Sinica, 2005, 28(3):431-434.)

[2] 钟于义. 超低速转台控制方法的研究与实现[D]. 哈尔滨：哈尔滨工业大学，2007. (Zhong Yuyi. Research and Implementation of Control Method for Ultra-Low Speed Turntable[D]. Harbin: Harbin Institute of Technology, 2007.)

[3] 方辉煜，李启全，吴永刚,等. 防空导弹武器系统仿真[M]. 北京：宇航出版社，1995. (Fang Huiyu, Li Qiquan, Wu Yonggang, et al. Air Defense Missile Weapon System Simulation[M].Astronautics Press, Beijing, 1995.)

[4] 张新邦.航天器半物理仿真应用研究[J].航天控制，2015，33(1)：77-83. (Zhang Xinbang. The Research on Application of Hardware in the Loop Simulation for Spacecraft [J]. Aerospace Control, 2015, 33(1):77-83.)

[5] Acutronic Three Axis Motion Simulator, Series AC3357-140, TN-2267A[Z].

TheDiscussionontheQuestionofServoTurntablePerformance

Zhang Xinbang, Zeng Haibo, Zhang Jinjiang, Zhu Zhibin

Beijing Institute of Control Engineering, Beijing 100190, China

Therearesomeresearchesonthecontroltechniqueforlowspeedperformanceofservoturntable.Butthereisfewdiscussionforhowtodescribe,testandsizeupthelowspeedperformance.Itispresentedthat“thelowestsmoothspeed”and“thepositionprecisionundercontrolinlowspeed”canbeusedtodescribethelowspeedperformancewithquantizedinformation.Duringthetestofturntabledynamicresponseperformance,besidethefrequencyresponsemethod,thefast-stopmethodisusedasafurthertest.Thedynamicresponseperformanceofturntablecanbeimprovedbyusingmulti-signalinputs(thesignalsofposition,speedandaccelerationaresenttoturntablecontrolsystemtogether)andappropriatefeed-forwardmethod.Theperformancecanbefurtherimprovedbyusingmulti-signalinputsandcompositecontrolmethod.

Servoturntable;Lowspeedperformance;Dynamicresponse

V448.25+3

A

1006-3242(2017)05-0064-04

2016-12-23

张新邦(1946-)，男，上海青浦人，研究员，主要研究方向为航天器控制系统仿真；曾海波(1972-)，男，广东五华人，博士，研究员，主要研究方向为航天器制导导航与控制；张锦江(1973-)，男，黑龙江富锦人，博士，研究员，主要研究方向为航天器控制制导与仿真；朱志斌(1981-)，男，河南人，博士，高工，主要研究方向为航天器智能控制与仿真。