具有时变时延的网络控制系统的量化控制*

宋 娟

1.苏州科技大学数理学院，苏州215009 2.苏州科技大学天平学院，苏州215009

具有时变时延的网络控制系统的量化控制*

宋 娟1,2

1.苏州科技大学数理学院，苏州215009 2.苏州科技大学天平学院，苏州215009

研究了具有时变时延的网络化控制系统的量化控制问题。首先在考虑量化因素的影响下,基于网络传输环境建立了一类包含时延和量化信息的新的网络化控制系统模型；其次运用Lyapunov 稳定性理论和线形矩阵不等式(LMI)方法, 给出系统稳定性条件和对数量化控制器的设计方法；最后通过仿真实验证明了该方法的有效性。

网络控制系统；时延；量化；Lyapunov原理；LMI

通过实时网络形成闭环的反馈控制系统被称为网络控制系统(Networked Control System,NCS)。由于结构简单和灵活, 网络控制系统在信息科学、生命科学及军事及航空航天等诸多领域得以广泛应用。但是, 网络控制系统中不可避免地存在网络诱导时延、数据包丢失和时绪错乱等不确定因素[1-3], 这不但给系统性能带来消极影响,甚至可能导致系统失去稳定。近年来,具有时延的网络控制系统控制问题已成为控制控制领域的一个研究热点[4-10]。

文献[5]基于状态中包含多重连续延时成分的延时模型，针对NCS 提出一种新的延时系统论方法。文献[6]研究了一类具有多传输通道网络化系统的控制问题, 在多传输通道的时延为定常的情况下分析了系统稳定性。文献[7]针对随机延时，提出了延时估计和在线获得延时数据2种方法。 先利用z 变换处理延时,由等价关系产生残差；再通过参数设计解耦干扰向量，从而对网络化控制系统的故障进行有效诊断。文献[8]提出一种同时设计控制器和通信策略的方法，共同镇定一个线性NCS ,将延时和通信受限同时存在的线性NCS 建模为等价的线性时变系统。文献[9]给出了广义被控对象的离散模型，利用Lyapunov方法给出闭环系统渐近稳定的充分条件，并基于LMI 求解状态反馈控制律。但以上文献中针对NCS 的分析及设计都假设信号能直接传输且为无损传输,而在NCS应用中,公共网络有限的传输能力必然会对在线控制产生巨大的消极影响,因此数据的量化处理是必要的。 目前对NCS 的量化控制器的分析和设计尚待解决。

本文在传感器与控制器之间设置对数量化器, 控制器使用量化后产生的信息进行计算, 计算所得控制输入经后向反馈网络传输到执行器, 并作用于被控对象。 在同时考虑网络时延和量化的情况下提出了系统稳定性条件和量化控制器的设计方法。

1 具有对数量化器的NCS建模

具有量化器的NCS的基本结构如图1所示。

图1 具有量化器的NCS的基本结构

图1中,τsc为传感器-控制器端时延,τca为控制器-执行器端时延。 总的诱导时延为τ=τsc+τca。 考虑如下所示的线性被控对象:

(1)

其中，x∈Rn,u∈Rm和y∈Rr分别为状态向量、控制输入向量和输出向量,Ao,Bo和C为适当维数的矩阵。为了便于讨论，现作如下假设：

假设1 在传输过程中存在时变时延，时延有界且不超过采样周期, 即τ(t)∈[0,T], 其中T为采样周期。

假设2 传感器采用时间驱动, 控制器和执行器均采用事件驱动。

图2 网络控制系统中信号传输时序

网络控制系统中信号传输时序如图2所示。 基于NCS的结构和如上假设, 在一个采样周期内, 系统的输入不是一个单一常数,而是一个分段常数。 在一个周期内, 控制输入可以表示为：

(2)

其中，tk是第k个采样时刻,τk是对应的时延。系统(1)可以等价于如下离散模型:

(3)

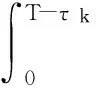
由于τk是不确定的,故B1和B2也是时变的。因此,式(3)中含有不确定参数, 文献[10]给出了式(3)的等价模型：

(4)

本文考虑如下量化水平集：

其中，λ∈(0,1)。对数量化器qλ(·):R→Qλ, 具体定义如下:

(5)

考虑到网络传输资源的有限性，传感器采样的数据需量化处理后才能经网络传输到控制器。 本文考虑如下对数编码/解码器：

(6)

(7)

其中，K为待设计的量化控制器增益。

将式(7)带入式(4)可得：

(8)

另一方面, 由式(6)可得：

(9)

(10)

z(k+1)=Ψz(k)

(11)

2 量化控制器设计

引理1[11]对于任意矩阵W,M,N,F(t)，满足FTF≤I，给定常数ε>0, 则如下不等式成立

W+MF(t)N+NTFT(t)MT≤
W+εMMT+ε-1NTN

(12)

定理1 对于系统(11), 给定标量ε>0和σ>0, 若存在对称正定矩阵X及矩阵W, 满足如下线性矩阵不等式：

(13)

则NCS式(11)渐进稳定, 且量化控制增益为K=WX-1。

证明：首先选取Lyapunov函数如下：

v(k)=zT(k)Pz(k)

(14)

沿系统式(11)的任意轨线向前作差分，必有

Δv(k)=v(k+1)-v(k)
=zT(k+1)Pz(k+1)-zT(k)Pz(k)
=zΤ(k)(ΨΤPΨ-P)z(k)

(15)

显然，当Δv(k)<0时, 则系统式(11) 稳定， 即ΨΤPΨ-I<0，根据Schur补原理可知，其等价于

(16)

其中，Ψ如式(11)所示。

式(16)可等价为：

(17)

由于不确定分量F满足:FΤF≤I。 利用引理1可得：

(18)

根据Schur补原理可得，

(19)

式(19)可等价为：

(20)

由于不确定分量Φ满足:ΦΤΦ≤I。利用引理1可得：

(21)

再次使用Schur补原理可得，

(22)

3 仿真算例

考虑如下倒立摆模型：

选取采样周期T=0.1s。 网络诱导时变时延如图3。 令量化参数λ=0.5， 即量化水平集为：

Qλ={3i}∪{0}∪{-3i},i为正整数。

选择参数α1=1.5,α2=-1.5,α3=-2,α4=1.6。 按文献 [10]的计算方式可得：

D=

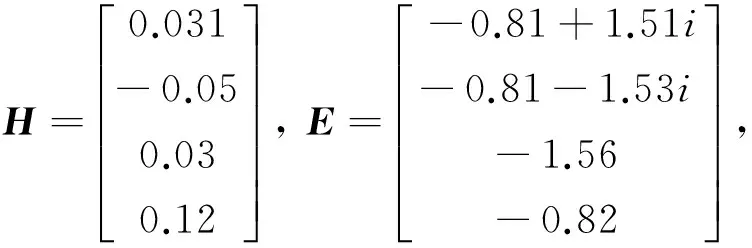
F=

显然满足条件：FTF

图3 NCS中的时变时延

4 总结

研究了一类在传感器-控制器端存在量化的时

图4 NCS的状态响应

延网络化控制系统的量化控制问题。 首先基于网络传输环境建立了一类包含时延和量化信息的新的闭环网络化控制系统模型。 其次运用Lyapunov 稳定性理论和线形矩阵不等式(LMI)方法, 给出系统稳定性条件和对数量化控制器的设计方法。最后通过仿真实验验证了本文方法的有效性和可行性。

[1] Luan X, Shi P, Liu F. Stabilization of Networked Control Systems with Random Delays[J]. IEEE Transactions on Industrial Electronics, 2011，58(9):4323-4330.

[2] Yu H, Antsaklis P J. Event-triggered Output Feedback Control for Networked Control Systems Using Passivity: Achieving L2 Stability in the Presence of Communication Delays and Signal Quantization[J]. Automatica, 2013, 49(1): 30-38.

[3] Xia Y, Xie W, Liu B, et al. Data-driven Predictive Control for Networked Control Systems[J]. Information Sciences, 2013, 235 (20): 45-54.

[4] Luck R , Ray A. An Observer-based Compensator for

Distributed Delays[J]. Automatica , 1990 , 26 (5) : 903-908.

[5] Gao H J , Chen T W , Lam J . A New Delay System Approach to Network-based Control [ J ] . Automatica,2008, 44(1): 39-52.

[6] 宋洪波, 刘国平. 具有多传输通道系统的网络化预测控制[J]. 控制理论与应用, 2015 ,32(7): 912-917.(Song H B, Liu G P. Networked Predictive Control for Systems with Multiple Communication Channels[J].Control Theory and Applications, 2015 ,32(7): 912-917.)

[7] 郑英, 方华京, 谢林柏, 等.具有随机时延的网络化控制系统基于等价空间的故障诊断[J]. 信息与控制, 2003, 32(2): 156-159. (Zheng Y, Fang H J , Xie L B , et al. Parity Space Based Fault Diagnosis of Networked Control System with Random Delay [J].Information and Control, 2003, 32(2): 156-159.)

[8] Zhang L , Hristu-Varsakelis D. Communication and Control Co-design for Networked Control Systems[J]. Automatica, 2006, 42(6): 953-958.

[9] 樊卫华, 蔡骅, 陈庆伟, 等.时延网络控制系统的稳定性[J]. 控制理论与应用, 2004, 21(6): 33-37.(Fan W H, Cai H, Chen Q W, et al. Stability of Networked Control Systems with Time Delay [J]. Control Theory and Applications, 2004, 21(6): 33-37.)

[10] 谢成祥,樊卫华,胡维礼.一类短时延网络控制系统的建模和控制方法. 南京理工大学学报(自然科学版), 2009, 33(2)：156-160.( Xie Chengxiang, Fan Weihua, Hu Weili.Modeling and Control Method of a Class of Networked Control Systems with Short Time-delay[J]. Journal of Nanjing University of Science and Technology, 2009,33(2) : 156-160.)

[11] Zhu Qixin, Lu Kaihong.H∞Guaranteed Cost Control for Networked Control Systems under Scheduling Policy Based on Predicted Error[J].Mathematical Problems in Engineering, 2014：1-14.

QuantizedControlofNetworkedControlSystemswithTime-VaryingDelay

Song Juan

Suzhou University of Science and Technology, Suzhou 215009, China

Theproblemofquantizedcontrolofnetworkedcontrolsystemswithtime-varyingdelayisdiscussed.Basedonthenetworktransmissionenvironment,anewnetworkedcontrolsystemwithdelayandquantizationconsideredisfirstlymodeled.Then,byusingLyapunovstabilitytheoryandlinearmatrixinequality(LMI)approach,thestableconditionofthesystemisgivenandthemethodfordesigninglogarithmicquantizationcontrollerisproposed.Finally,simulationsareimplementedtodemonstratetheeffectivenessofthemodel.

Networkedcontrolsystem;Delay;Quantization; Lyapunovtheory; LMI

TP273

A

1006-3242(2017)05-0015-04

*国家自然科学基金资助项目(51375323)；苏州科技计划资助项目(SYN201509)；江苏‘青蓝工程’资助；江苏省高等学校自然科学研究项目资助(17KJD110009)；苏州科技大学天平学院青年科研基金项目(TPQN2016002)

2017-01-04

宋娟(1982-)，女，山西翼城人，硕士，讲师，主要研究方向为非线性系统理论与应用,网络化控制系统。