基于武汉地层盾构隧道施工的Peck经验公式修正

余 朔 卢国胜

基于武汉地层盾构隧道施工的Peck经验公式修正

余 朔1卢国胜2

（1.同济大学交通运输工程学院，201804，上海；2.西南科技大学环境与资源学院，621010，绵阳//第一作者，博士研究生）

隧道施工引起的地表沉降大小受到很多因素的影响，Peck经验公式中，参数的变化会使预测结果容易出现较大的偏差。以武汉地铁3号线盾构下穿铁路工程为依托，结合施工和土质参数及实测沉降数据，采用回归分析的方法对Peck经验公式作线性拟合并进行了对比分析，同时研究了沉降槽宽度系数与盾构切口距监测断面间距的关系以及地表最大沉降量与注浆倍数的关系，并拟合得出了相应的函数计算式来对原系数进行修正。实践验证表明，修正后的Peck公式能很好地预测隧道施工引起的地表沉降，且预测曲线与实测曲线吻合度高。

盾构隧道施工；地表沉降；Peck经验公式；系数修正

盾构施工往往会引起地表发生变形及开裂。因此，预测及控制盾构施工对地表沉降的影响显得尤为重要。目前研究地表沉降预测的方法有很多，主要有 Peck 经验公式法［1］、解析法［2］、神经网络法［3］、随机介质法［4］以及数值模拟法［5-6］等。 Peck经验公式法具有简便、高效的特点，是目前运用较广泛的方法。但该计算方法涉及的系数与土层条件及施工参数有关，因此Peck经验公式中的各个系数都较难确定。文献［7］采用Peck经验公式对武汉地区的实测沉降数据进行了回归分析，对该地区的沉降槽宽度系数及地层损失率给出了建议上限值；文献［8］利用最小二乘法对武汉地区的实测数据进行了Peck曲线拟合，得出了该地区不同隧道埋深对应的沉降槽宽度系数的取值范围；文献［9］根据Peck理论对武汉地区的实测沉降数据进行了拟合分析，得出了地表最大沉降量与盾构切口距离以及注浆量有明显的相关性。上述文献的研究或是对Peck公式中各个系数给出取值范围，或是对系数的影响因素进行相关性分析，但并不能精确地预测出武汉地区的地表沉降。因此，为了满足武汉地区盾构施工的需要，本文以该区域工况的地表沉降实测数据为基础，将拟合前后的Peck经验公式进行对比分析，同时对Peck经验公式的相关系数进行修正，为相关工程提供参考。

1 工程简介

武汉地铁3号线盾构始发于兴业路站，出站后穿越密集的淌湖村居民区，然后再下穿京广上下行线、京广汉口客联上行线、合武上下行线、京广汉口联络下行线等铁路线密集带，然后达到二七路站。盾构区间起止里程为右DK 23+479.502～右DK 24+583.500。其中，隧道左、右线的间距为9 m，盾构中心埋深约为12 m，盾构直径为8 m。盾壳厚度为0.02 m。

该盾构区间位于长江Ⅰ级阶地，隧道主要穿越粉质黏土、粉土、粉砂互层及粉细砂层，表层覆土主要为杂填土、素填土，地质参数如表1所示。

表1 地质参数表

为保证铁路运营安全，在盾构穿越的过程中，于铁路线路上布置监测点进行全天候的监测。其中，每条线路布置7个监测点，总计42个；监测点距盾构隧道中心线的距离分别为6 m、10 m，12 m，监测仪器选用全自动全站仪SOKKIA-NET05。监测点平面布置图如图1所示。

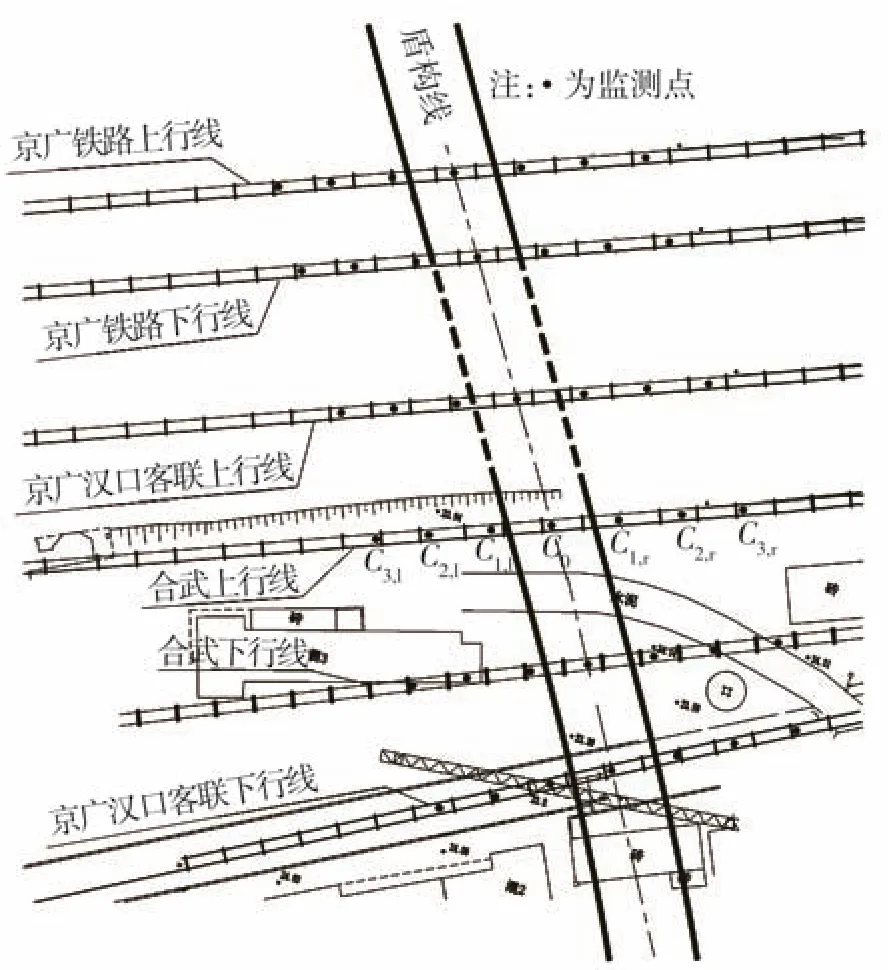
图1 监测点平面布置图

2 Peck经验公式参数的确定

1969年，Peck提出隧道开挖形成的横断面类似于高斯分布曲线的沉降形态，如图1所示，且在不排水的情况下，其地层损失体积Vl约等于地面沉降形成的槽状体积VS［10］，其地表横向沉降槽示意图如图2所示。

图2 地表横向沉降槽示意图

图2 中，距离隧道中心线x处的地表沉降值为：

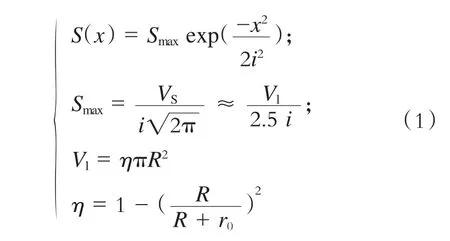
式中：

x——距隧道中心线的距离；

i——地表沉降槽宽度，即沉降槽曲线的反弯点距离隧道中心线的水平距离；

Vl——地层损失体积；

η——地层损失率；

r0——盾壳厚度。

本工程中，R 为 3 m，r0为 0.02 m，代入式（1）中可算出η=1.32%。i与土质条件及施工等因素有关。文献［11］给出了国内外学者提出的不同土质条件下i的计算公式，如表2所示。

表2 不同土质条件下i的计算公式

表2中的几类土体在武汉隧道施工过程中均有所涉及。因此，对表2中由不同计算公式计算出来的i取平均值作为武汉地区的沉降槽宽度。已知H为12 m，通过计算得出i=5.29 m，再将i值代入式（1）中，则Peck经验公式可表示为：

3 基于实测数据的Peck经验公式回归分析

由于Peck经验公式为非线性函数，为了便于回归分析，需对原公式进行线性转换［12］，即：

令＾a和＾b分别为常数项、线性系数的最小二乘估计值，则Peck经验公式的线性回归模型可表示为：

选取盾构刀盘穿越合武上行线30 m后的实测沉降数据进行回归分析，分析结果如表3所示。

表3 合武上行线实测沉降数据线性转换

图3为Peck经验公式修正拟合曲线与Peck经验公式曲线及实测数据对比图。由图3可知，经线性拟合后的数据与实测数据较吻合；而Peck经验公式预测曲线与实测数据相差较大，原因是由于注浆量及盾构刀盘和断面间距的变化会使i和Smax产生波动，因此计算得到的沉降数据会存在较大的误差。

通过计算可以得出＾a为2.739 95，＾b为0.009 34，则回归分析后的线性函数为：

将＾a和＾b代入式（4），得到Smax为15.486 1 mm，i为 10.349 81 m；将 Smax和 i代入式（1）中，则拟合后的Peck公式可表示为：

图3 Peck经验公式修正拟合曲线与Peck经验公式曲线及实测数据对比图

4 Peck经验公式的修正

4.1 沉降槽宽度系数is

盾构在施工过程中，is并不是固定不变的。因此，为了研究is与盾构切口距沉降点距离的关系，选取合武上行线进行分析。统计了隧道轴线中心上方及两边与盾构切口不同间距时的地表沉降数据，如表4所示。将统计得到的沉降数据进行线性回归分析，得出监测断面距盾构切口不同间距的is，并对其进行系数转换，如表5所示。

图4为沉降槽宽度系数与盾构切口距监测断面间距关系示意图。从图4可看出，is的变化范围为盾构监测断面前后30 m以内，30 m以外趋于稳定。该曲线分布近似于分段线性函数，且间断点在该断面处。因此，对该曲线进行分段线性回归，可计算得出：

同时为了与Peck经验公式进行对比分析，将监测断面距盾构切口不同间距的is与Peck公式计算得出的i进行数据转换（见表5），得出两者之间的转换方程，即：

表4 不同s值时合武上行线沉降数据汇总 mm

考虑到计算的简便，提出刀盘间距系数。并对式（8）进行简化，则修正后的is可表示为：

is=0.59（0.033βs+1.616 3），-30≤ s≤30 （9）式中：

β——刀盘间距系数。当-30≤s≤0，取值为1；当 0 ＜ s≤ 30，取值为 1/3。

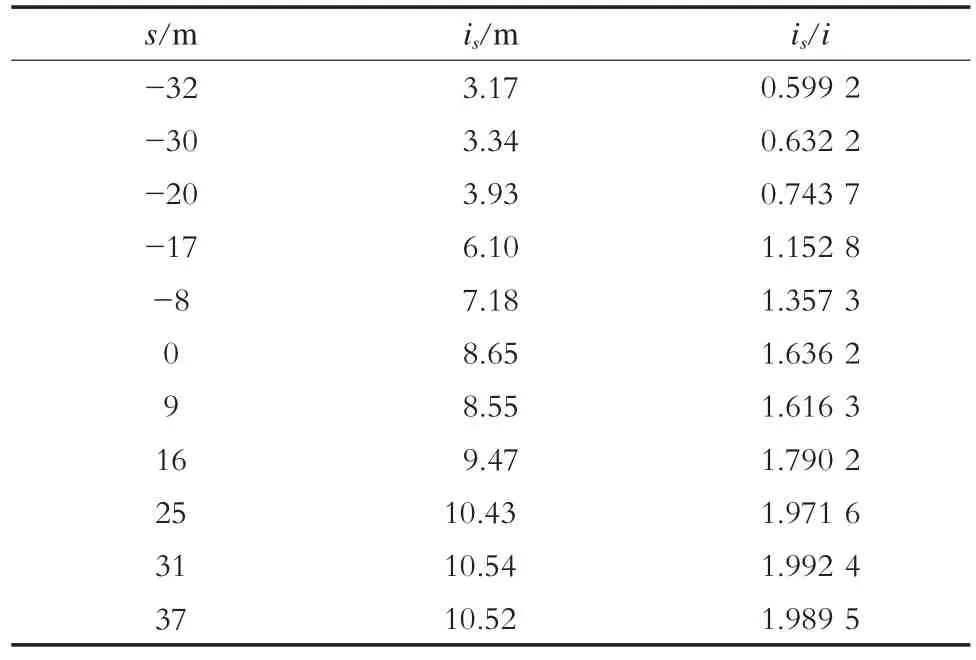
表5 回归分析及系数转换

图4 沉降槽宽度系数与盾构切口距监测断面间距关系示意图

4.2 地表最大沉降量Smax，k

盾构在施工过程中，盾构与管片之间的尾部空隙会引起土体发生沉降及位移，及时进行同步注浆能有效控制地表的沉降及位移。因此，地表的最大沉降量与注浆量的大小有关，在实际工况中均以尾部间隙的注浆倍数k作为注浆量的参考数据。表6为不同监测断面处地表最大沉降量与注浆倍数情况。图5为地表最大沉降量与k关系示意图。从图5可看出，Smax，k与k成反比，且曲线函数类似于对数函数，对数据进行拟合得出：

同时其与Peck经验公式中的最大地表沉降量进行了数据转换，如表6所示。回归分析后得出：

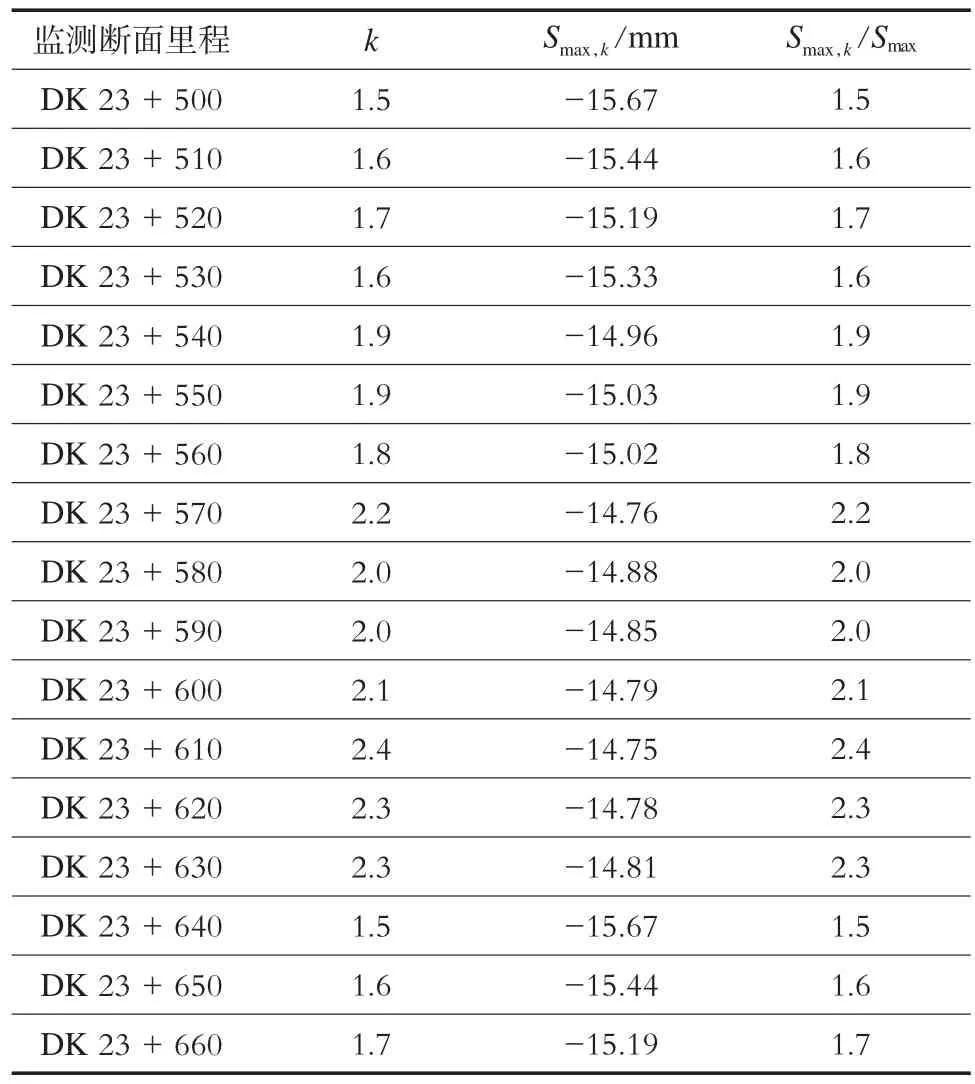
表6 不同监测断面处地表最大沉降量及注浆倍数k情况

图5 地表最大沉降量与注浆倍数关系示意图

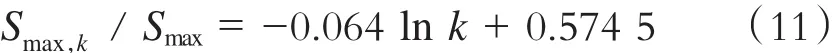
因此修正后的Peck公式可表示为：

4.3 修正公式的检验

为了验证修正公式的适用性，将合武下行线的实测数据与Peck修正公式计算得出的数据进行对比，如图6所示。由图6可知，除了个别点与计算结果吻合度不高，其余点的精度误差均控制在7%以下，说明修正后的Peck公式能很好地对该地区的地表沉降进行预测。

图6 合武下行线Peck修正数据曲线与实测数据对比

5 结论

（1）以武汉地铁3号线盾构下穿铁路的实测沉降值为依据，通过线性回归对Peck经验公式进行拟合。对比分析表明，拟合后的预测曲线与实测值的吻合度相比Peck经验公式曲线较好。因此，对沉降槽宽度及最大地表沉降量两个系数进行分析并修正。

（2）借助回归分析法，通过研究沉降槽宽度系数和盾构切口与监测断面间距之间的关系发现，沉降槽宽度系数的变化范围为监测断面前后30 m之内，且该曲线近似于分段线性函数，间断点在该断面处，其斜率大小与刀盘间距系数有关；通过研究不同监测断面最大地表沉降量与注浆倍数的关系发现，最大地表沉降量与注浆倍数成反比，且拟合结果类似于对数函数分布。

（3）通过实际工况对比研究表明，Peck修正公式计算得到的数据与实测数据的吻合度较高，精度误差小，能够很好地运用于实际工程当中。

［1］ ATTEWELL P B，WOODMAN J P.Predicting the dynamics of ground settlement and its derivatives caused by tunneling in soil［J］.Ground Engineering，1982，15（8）：13-20，36.

［2］ LOGANATHAN N，POULOS H G.Analytical prediction for tunneling-induced ground movements in clay ［J］.Journal of Geotechnical&Geoenvironmental Engineering，1998，124（9）：846-856.

［3］ 金长宇，马震岳，张运良，等.神经网络在岩体力学参数和地应力场反演中的应用［J］.岩土力学，2006，27（8）：1263－1271.

［4］ 朱忠隆，张庆贺，易宏传.软土隧道纵向地表沉降的随机预测方法［J］.岩土力学，2001，22（1）；56-59.

［5］ 张海波，殷宗泽，朱俊高.地铁隧道盾构法施工过程中地层变位的三维有限元模拟［J］.岩石力学与工程学报，2005，24（5）：755-760.

［6］ 于宁，朱合华.盾构隧道施工地表变形分析与三维有限元模拟［J］.岩土力学，2004，25（8）：1330－1334

［7］ 陈春舒，夏元友.Peck公式在长江一级阶地盾构中的适用性研究［J］.武汉理工大学学报，2013，35（9）：85-90.

［8］ 胡斌，莫云，胡新丽，等.Peck法在武汉地铁隧道地表沉降预测中的适用性分析［J］.工程勘察，2012，40（7）；6-10.

［9］ 冯虎，张文成，孙士玲.武汉地铁2号线盾构施工对地表沉降影响分析［J］.施工技术，2010，39（11）：75-78.

［10］ PECK R B.Deep excavation and tunneling in soft ground［C］//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City：SMFE，1969：225-290.

［11］ 谭文辉，于江，孙宏宝，等.地铁7号线车站地表施工沉降的Peck 公式修正［J］.地下空间与工程学报，2015，11（S1）：200-204.

［12］ 陈明，陈子毅，汪嘉冈.数理统计讲义［M］.上海：复旦大学出版社，2006.

Peck Empirical Formula Modification for Subway Tunnel Construction in the Stratum of Wuhan City

YU Shuo，LU Guosheng

There are many factors that could affect the ground subsidence during tunnel construction，due to the variability of parameters in Peck empirical formula，the prediction of ground subsidence tends to produce greater deviation.In this paper，based on the subway shielding of Wuhan metro Line 3 which crosses under the existing railway line，and combined with the construction parameters，soil parameters and measured settlement data，the regression analysis method is adopted to fit with the linear transformation of Peck empirical formula，the fitting formula is also compared with the measured surface subsidence data.At the same time，the relationships between the settlement trough width coefficient and the distance of shield tunnel incision，between the maximum ground settlement and the grouting multiples are studied，corresponding function calculation formula is gained through fitting to modify the original coefficient.The results show that the revised Peck formula can better predict the ground settlement caused by tunnel construction，the alignment of prediction curve and measured curve is also higher.

shield tunnel construction； ground subsidence；Peck empirical formula；coefficient modification

TU433：U455.43

10.16037/j.1007-869x.2017.10.003

Author′s address School of Environment and Resources，Southwest University of Science and Technology，621010，Mianyang，China

2015-11-10）