以学定教，提升数学复习课堂效率

钱瑶强

[摘 要] 以学定教，就是根据学生的学习情况来确定教师的教学情况. 在高中数学复习教学中，根据学生的学习情况，教师再来制定相应的复习策略与计划，借此提高复习效率. 文章从梳理知识、结合偏差、多元类比、问题引领等几方面阐述了在高中数学复习教学中，本着“以生为本，以学定教”的原则开展教学，从而有效地提升数学课堂效率.

[关键词] 高中数学；数学教学；以学定教；课堂效率

随着高中教育的不断改革，提升学生的自学能力变得尤为重要. 传统的教学模式是教师“教”，学生“听”，没有培养学生自学的能力. 通过教师的不断探索，发现了“以学定教”这一科学的新型教学模式：根据学生的实际学习情况来确定课堂教学和复习的内容、方法，充分将教师的“教”与学生的“学”有效地结合起来，融为一体，从而不断地提高数学复习课堂的效率.

梳理知识，把握脉络

数学这一学科与其他学科不同，数学教材中的知识点是有层次的，而且是由浅显易懂到深邃复杂的，一个逐步递进的过程. 高中数学后面章节的新知识大多是以前面的旧知识作为基础进行拓展延伸构建而成的内容，所以在学习新的数学知识之前，带领学生对数学知识进行复习，梳理相关知识是十分有必要的. 这样做，一方面有利于学生把握新旧知识的逻辑关系，找准数学的方向和脉络；另一方面对学生理解新的数学知识做好了铺垫，让学生理解新知识变得更加容易. 对知识的梳理可以利用课本进行剖析，通过教师和学生合作归纳、总结等，帮助学生摸清知识的脉络.

例如，在讲述“三角函数的变化”相关内容时，需要让学生明白三角函数y=sinx是通过怎样的变化成为函数y=sin（Ax+B）的. 笔者首先带领学生回忆之前课堂上学过的正弦函数y=sinx的相关性质，等学生理解了正弦函数之后，笔者再向学生归纳三角函数的相关变化的方式主要是平移、伸缩和振幅. 这三个变换步骤中的重点是三角函数先平移后压缩形成的函数图像，与先压缩后平移形成的函数图像是有所区别的，这是学生难以理解的重点. 鉴于上述原因，笔者结合数学教材上的例题，带领学生一起进行图形的变换. 让学生有了一定的理解之后，再进行复杂例题的拓展训练. 笔者让学生练习如何将y=sin（Ax+B）的函数图像进行相关变化，从而得到正弦函数y=sinx的图像. 学生有了之前的经验，进行逆向思考，从而得出答案.

在上述教学过程中，笔者首先带领学生复习了正弦函数的相关性质，让学生把握主题的方向，之后再带领学生对函数变换问题进行思考，最后设置难度微高于例题的题目，供学生练习巩固，内化三角函数进行变换的知识. 整节数学课堂中，不仅仅只是笔者在课堂上进行了讲述，还有笔者和学生在一起讨论，以及学生自己动脑进行解题的过程，将教师的引导作用充分发挥了起来，真正做到了数学课堂上的“以学生为主”和“教学结合”的原则.

结合偏差，针对练习

高中数学的课堂教学需要符合科学性、渐进性、针对性的基本原则. 简单来说，就是教师的课堂教学不仅要符合学生的认知规律和新课标对学生素质教育的要求，在教学过程中更要结合学生自身的掌握数学知识的能力和自学复习的情况，以及学生学习的偏差，有针对性地展开循序渐进的练习. 另外，在教学课堂中，教师还需要观察学生回答问题和做题的情况，掌握学生理解的偏差之处，从而在课下引导学生复习时，布置有针对性的数学题目对学生进行训练，让学生意识到自己的问题所在，从而提高掌握知识的能力.

例如，在讲述对数函数相关性质时，笔者在课堂上发现学生对对数函数的单调性理解不透彻，鉴于课堂时间有限，笔者给学生留下了一道数学练习题，让学生课下练习巩固，进行复习. 问题：（1）a为何值时，函数f（x）=-ax+2在定义域（-∞，1）上单调递减？（2）a为何值时，函数f（x）=lg（-ax+2）在定义域（-∞，1）上单调递减？（3）a为何值时，对数函数f（x）=loga（-ax+2）在定义域（-∞，1）上单调递减？这道题目的设置由易到难，有了第一问的铺垫，很多学生都可以做出第二问，第三问就需要学生动脑思考，进行探索了.

上述教学过程中，笔者发现学生学习不到位的地方，通过课下习题训练学生，让学生熟练掌握相关知识. 而且课下问题的设置是渐进性的，可以激发学生主动探索的兴趣和欲望.

多元类比，深度认知

伟人康德说：“每当理智缺乏可靠性的论证思路时，类比这个方法往往能够指引我们前进. ”在数学的教学中，我们不难发现多元类比这种数学思想和方法是发现一些数学定理和公式的重要渠道，也是对数学进行创新和开拓数学知识领域的重要手段之一. 通过对数学知识的多元类比进行有效的课后复习，不仅可以让学生加深对课堂内容的深刻理解，深度认知数学知识点，提高学生的学习效率，也能够培养学生的自学复习能力、探究钻研的数学能力.

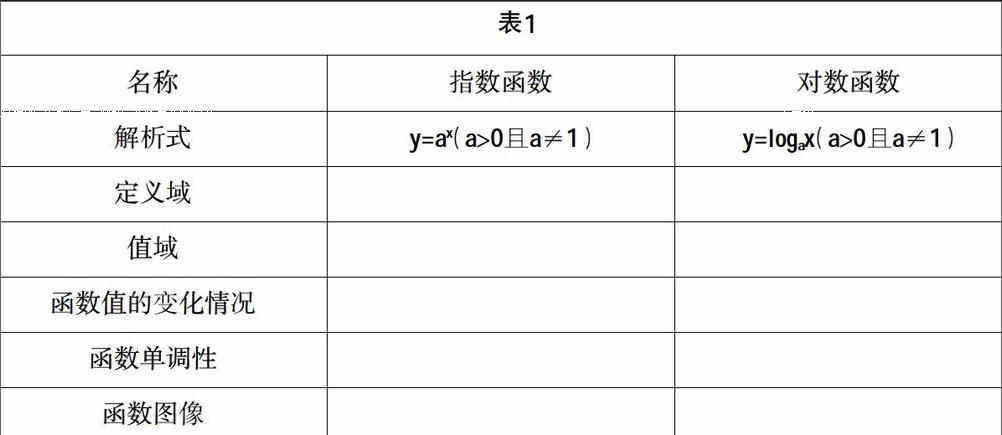
例如，在学习“对数函数”的相关内容时，笔者在课堂上依次对指数函数的定义域、值域、函数值的变化情况，指数函数的单调性，指数函数的图像等性质进行了仔细的讲解. 因为学生之前学习过对数函数的相关内容，而且对数函数与指数函数两个函数是互为反函数的. 所以在课堂结束时，笔者在黑板上画出函数性质对比表（表1），让学生自己在课上，完成函数性质对比表，把指数函数与对数函数的相关性质进行对比，发现其中的联系和区别.

在上述教学中，学习完指数函数相关内容之后，笔者引导学生在课上复习时将指数函数的相关性质与对数函数进行类比，发现其中两个函数之间存在的联系与区别，提高了学生复习的效率. “类比是一个伟大的引路人”是著名的数学家波利亚的话. 从中我们可以知道，多元类比这一数学思想的重要性. 教师在数学课堂中应渗透多元类比这一思想，在学生课上复习时能够对新学的数学知识进行多元类比，一方面让学生深入理解新学的数学知识，另一方面让学生勇于探索，拓展延伸数学知识面.

问题引领，意义建构

众所周知，高中数学的核心思维就是数学问题. 从某种程度上说，高中数学主要就是培养学生利用各种数学方法来解决数学问题的能力，所以数学问题设置需要贯穿在教师教学过程中的主线上. 问题引领的复习策略主要是指在数学教师精心设计的数学问题引导下对课上的数学知识进行科学有效的复习，让学生能够清晰地理解、吸收数学知识并且帮助学生构建数学概念体系，提高学生的复习效率.

例如，在讲述“三角函数”相关内容时，笔者首先提出问题：sinα与sin（α+π，cosα与cos（α+π），tanα与tan（α+π）的关系是什么？学生开始动脑思考，总结出公式：sin（α+π）=-sinα，cos（α+π）=-cosα，tan（α+π）=tanα. 这时笔者又提出问题：（1）公式中的角α必须是锐角吗？（2）每个公式两边的三角函數名称有什么关系？（3）若将α当作锐角，那么α+π在第几象限，这时α+π的三角符号又是怎样一种情况？在学生动脑思考之后，归纳为公式两边三角函数的名称相同，如果将α当作锐角，各个公式中的符号与α+π的三角函数值的符号相同. 最后，笔者帮助归纳总结为“函数名不变，符号看象限”这一数学规律.

通过由易到难、富有层次的几个数学问题对学生进行引导之后，让学生在问题的引导下，一方面对初中的锐角三角函数进行复习，另一方面也总结了三角函数变换规律意义建构的目的. 另外，值得注意的是，教师在设计复习问题来启发学生思考的时候，数学问题的设置与表述需要根据课堂教学内容，要有针对性、有目的性，数学问题还应简明、清晰，能激发学生产生更多的创造性思维.

总而言之，数学知识需要学生的及时复习，并不断巩固. 而高效的复习课堂需要教师本着“以学生为主”这一原则，结合学生自身的学习情况，以学定教，让学生自主学习、探究学习，从而有效地提高课堂教学效率.endprint