2017年全国卷Ⅰ理科第13题的解法探究及应用*
2017-11-20
●
(山东省实验中学,山东 济南 250001)
2017年全国卷Ⅰ理科第13题的解法探究及应用*
●冯瑞瑶
(山东省实验中学,山东 济南 250001)
文章以2017 年全国卷Ⅰ理科第13 题为例,利用“转化”思想,提升有关平面向量问题的计算能力,探寻考题与教材中基本概念、基本公式和运算性质的关系,并把这一思想应用到求解2017 年浙江卷第15 题和江苏卷第12 题.
平面向量; 转化思想; 一题多解
向量在物理学等应用学科中有很多重要应用,是数学解析几何中教和学的重要内容,也是高考的重要考点之一.其主要考查形式是选择题和填空题,考查内容主要有向量的模、向量的夹角和向量的数量积的计算以及向量平行和垂直的判定等,难度适中,是考生必争之分.下面以2017年全国卷Ⅰ理科第13题为例,利用“转化”思想,给出多种解法,提升有关平面向量问题的计算能力.最后,笔者把这一思想应用到求解2017年浙江卷第15题和江苏卷第12题,说明“转化”思想是学好数学的一种重要思想,应用非常广泛.
1 问题提出
例1已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=______.
(2017年全国数学高考卷Ⅰ理科试题第13题)
该题主要考查向量的数量积和向量模的计算.
分析1由向量的内积满足乘法公式可知
(a+2b)(a+2b)=a2+4b2+4a·b,
再利用向量的模与平方的关系a·a=a2=|a|2,即可求出.
解法1(求模平方化)由|a+2b|2=(a+2b)(a+2b)=a2+4b2+4a·b=|a|2+4|b|2+4|a|·|b|cos 60°=12,解得

评注解法1的关键是把求向量的模转化为求向量模的平方,简称求模平方化.这是一个重要思想,在历年数学高考题中多有体现.例如,文献[1]利用这一思想给出了2013年浙江省数学高考理科第17题的多种解法.

(2013年浙江省数学高考理科试题第17题)
2.若非零向量a,b满足|a|=3|b|=|a+2b|,则向量a,b夹角的余弦值是______.
(2013年安徽省数学高考文科试题第13题)

(2013年江苏省数学高考试题第15题)

图1
分析2已知向量a,b的夹角为60°,从而向量a,2b的夹角也为60°.以向量a,2b为邻边作OBCA,作CD垂直于OA的延长线于点D(如图1),则|a+2b|=OC.
解法2(求模直角化)因为|b|=1,|2b|=2,又∠CAD=60°,∠ACD=30°,所以

从而

于是

点评在解法2中,把求向量的模转化为求直角三角形的斜边的长度,进而利用熟知的勾股定理即可求解.该解法简称求模直角化,它的优点是数形结合,不易出错,但在历年数学高考向量问题的解法探析中很少有人提出.例如,文献[1-5]给出了求解向量模的多种方法,对于“把求向量的模转化为求直角三角形斜边的长度”的想法尚未提及.
相关练习1.已知向量a,b的夹角为120°,|a|=2,|b|=1,则|a+2b|=_____.

3.已知向量a,b垂直,证明:|a+b|=|a-b|.
评注练习1是例1的变式,把条件“向量a,b的夹角为60°”改为“向量a,b的夹角为120°”.在一般情况下,只要告诉两个向量的长度和夹角,求有关向量的模,可优先考虑求模直角化的方法,这样做能事半功倍.由解法2知OBCA是菱形,∠COD=∠COA=30°,进而可得到解法3.
分析3易知向量a,a+2b的夹角为30°,通过计算向量a和向量a+2b的数量积即可得到a+2b的模.
解法3(求模数量化)因为
a·(a+2b)=|a|·|a+2b|cos 30°,
且
a·(a+2b)=a2+2ab=6,
得

所以

点评在解法3中,我们把求向量模的问题转化为求向量的数量积的问题,简称求模数量化.这里的关键问题是求出向量a,a+2b的夹角.

(2013年山东省数学高考理科试题第15题)
2.已知a,b是平面内的两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值是______.
(2008年浙江省数学高考理科试题第9题)
分析4以向量a的起点为原点、所在的直线为x轴建立直角坐标系,求出向量a,2b分别对应的坐标(如图2),即可求出向量a+2b的模.

a=(2,0), |2b|=2.
又∠BOC=60°,∠OBC=30°,从而

于是

故

点评在解法4中,通过建立直角坐标系,把向量问题转化为数量问题,简称求模坐标化.这里的关键问题是求出向量对应的坐标.

图2 图3
高考链接1.如图3,在ABCD中,已知||=8,||求
(2014年江苏省数学高考试题第12题)
(2013年天津市数学高考理科试题第12题)
读者可以参照参考文献[1,4,5]的方法对本题做进一步的研究.
2 方法应用
例2已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是______,最大值是______.
(2017年浙江省数学高考试题第15题)
分析部分考生以向量a,b为邻边作平行四边形,然后借助三角形的三边关系,得4<|a+b|+|a-b|<6.事实上,由此无法计算出|a+b|+|a-b|的最值.下面,利用“转化”思想求解|a+b|+|a-b|的最值.
解假设向量a,b的夹角为θ,则0≤θ≤π.因为|a|=1,|b|=2,所以
|a+b|+ |a-b|=

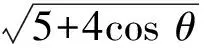
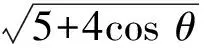
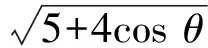

从而
16≤f2(θ)≤20,
即



图4
点评在求解过程中,若直接考虑f(θ),则很难精确计算出|a+b|+|a-b|的最小值和最大值,而把问题转化成f2(θ)的最值问题,可迎刃而解.

(2017年江苏省数学高考试题第12题)
分析由tanα=7,sin2α+cos2α=1可知





(1)

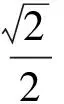
(2)


评注在求解过程中,用到了向量的模与平方的关系.另外,需要指出先求出sinα的原因在于:当0≤α≤π时,sinα的取值是非负,在开方运算中便于确定sinα的值.
对例3而言,还可以通过建立直角坐标系,把向量问题转化为数量问题,留给感兴趣的读者进行研究.
利用“转化”思想,给出了2017年全国数学高考卷Ⅰ理科第13题的4种解法,只当抛砖引玉,与大家分享.尽管方法不同,但是熟练运用这些方法的前提是对教材中关于向量的基本概念、基本公式和运算性质的熟练掌握.否则,再漂亮的思想和方法也将“失效”.因此,学好教材,弄清楚每一个基本概念、基本公式和运算性质并熟练运用才是关键.另外,通过上述对往届数学高考题的解析不难发现:“转化”思想是学好数学的一种重要思想.该思想在求解向量的模、向量的夹角和向量的数量积的运算中有广泛的应用,值得我们学习和借鉴.在学习过程中,自主地培养转化意识,这样才能在解题过程中灵活使用,做到又快又好地解题.
[1] 桂再安.一叶而知秋 一题一世界[J].数学教学通讯,2014(3):59-60.
[2] 蔡明.2010年浙江省数学高考理科试题第18题解读[J].中学教研(数学),2010(8):12-13.
[3] 张培强.四剂良方求a·b——探解一道高考向量数量积试题[J].新高考:高三数学,2014(11):8-9.
[4] 李学军,曲文瑞.大音希声 大象无形——基于2016年浙江省数学高考理科第15题[J].中学教研(数学),2016(12):43-45.
[5] 蒋海瓯.把握“长度”“方向”两要素 寻求“代数”“几何”双突破[J].中学教研(数学),2013(8):15-18.
2017-09-04
冯瑞瑶(2000-),女,山东济南人,高中学生.
O123. 1
A
1003 - 6407(2017)11-48-03
