回溯降维相干分布式非圆信号DOA快速估计

代正亮， 巴斌， 张彦奎， 崔维嘉， 王大鸣

解放军信息工程大学 信息系统工程学院， 郑州 450001

回溯降维相干分布式非圆信号DOA快速估计

代正亮*， 巴斌， 张彦奎， 崔维嘉， 王大鸣

解放军信息工程大学 信息系统工程学院， 郑州 450001

在相干分布式非圆(CDNC)信号波达方向(DOA)估计中，针对阵列输出矩阵扩展后维数增加带来的较大运算量问题，基于降维的多级维纳滤波(MSWF)技术，引入回溯优化思想，提出了一种快速估计算法。该算法首先利用信号非圆特性扩展阵列输出矩阵，然后通过MSWF递推分解快速求出信号子空间，避免了计算阵列协方差矩阵及特征分解，并且在递推过程中引入回溯优化机制提高了各级匹配滤波器的估计性能，最后由最小二乘(LS)或者总体最小二乘(TLS)得到DOA估计。仿真分析表明，所提算法与相干分布式非圆信号旋转不变子空间算法(CDNC-ESPRIT)性能相当，但复杂度得到了大幅度降低，相比于基于MSWF的非圆信号快速子空间(NC-MSWF-FS)算法，在较小的复杂度代价下大幅度提升了低信噪比时的估计性能，并且对初始参考信号的选取具有了较强的鲁棒性。

相干分布式信源； 非圆信号； 多级维纳滤波； 回溯优化； 递推分解

高分辨率的波达方向(Direction of Arrival， DOA)估计技术[1-3]是阵列信号处理的重要研究内容之一。传统的DOA估计算法都是基于点源模型提出的，但在雷达、声纳和移动通信等应用领域[4]，由于复杂环境下的散射、反射及衍射等原因导致大量的多径现象造成信号源在空间发生一定的角度扩展。此时，基于点源假设的传统DOA估计算法性能严重恶化[5-6]。为解决这一问题，一般采用一定参数化的分布式信源模型结合信源的分布特性进行DOA估计。分布式信源可以分为相干分布源(Coherently Distributed Source， CDS)和非相干分布源两种类型。迄今为止，针对上述两种分布式信源模型已发展出了众多有效的DOA估计算法。文献[7]首先将多重信号分类(MUltiple SIgnal Classification， MUSIC)算法推广到分布式信源，提出了分布式信源参数估计(Distributed Signal Parameter Estimator， DSPE)算法，但该算法需要进行二维谱峰搜索，计算复杂度高；在 DSPE算法的基础上，文献[8]利用基于泰勒级数展开的总体最小二乘旋转不变子空间算法直接求解分布式信源DOA估计，无需谱峰搜索，运算量较小。随后，又有相关学者相继提出波束形成类[9]、最大似然类[10]和稀疏重构类[11]等方法。

上述方法都是基于复圆信号特性的假设。然而，在现代通信中存在大量的非圆信号，如双相移相键控(Binary Phase Shift Keying， BPSK) 以及最小移频键控(Minimum-Shift Keying， MSK)等调制信号[12-13]。近年来，利用信号非圆特性提高分布式信源 DOA估计性能的研究引起了相关学者的关注。文献[14]在分布式信源模型中引入信号的非圆性质，提出了基于稀疏表示的相干分布式非圆信号参数估计，在低信噪比和有限快拍下具有较好的性能，但随着信噪比的提升，算法性能提升不明显，同时该算法需要进行多维稀疏重构，导致其复杂度较高。文献[15]针对相干分布源，提出了基于非圆信号和圆信号混合入射的DSPE算法，估计性能得到了提升，但该方法采用二维谱峰搜索的方式，运算量过大。为了降低复杂度，文献[16]提出了相干分布式非圆信号旋转不变子空间(Coherently Distributed Noncircular Source ESPRIT， CDNC-ESPRIT)算法，无需谱峰搜索，可以直接解算出DOA估计。尽管如此，由于利用非圆特性将阵列输出信号矢量维数进行了扩展，并且现有的这些子空间算法需要计算协方差矩阵和特征分解，因此复杂度仍有待降低。

多级维纳滤波(Multi-Stage Wiener Filters， MSWF)是一种低复杂度的降维技术[17]，被广泛应用在信号处理领域。它以简单的乘加过程代替了复杂的特征分解，利用其正交分解的特性可以快速估计信号或噪声子空间。文献[18]将MSWF应用到阵列的子空间分解中，并指出经前向递推分解得到的匹配滤波器可作为信号子空间基的估计值，但要求目标的训练序列或信号波形是先验已知的，在实际环境中实用性不高。文献[19-20]在点源模型下提出了一类基于MSWF的非圆信号快速子空间(NC-MSWF-FS)算法，运算量大幅度降低，并且通过观测数据构造初始参考信号，无须信号波形等先验信息，但该方法由于参考信号不可避免地引入噪声，MSWF递推分解过程中的匹配滤波器是次优的，导致算法在低信噪比时性能较差。

本文考虑相干分布式非圆信号，首先利用信号非圆特性扩展阵列输出矩阵，然后基于回溯优化的MSWF技术递推分解快速求出信号子空间，最后由最小二乘(Least Squares, LS)或总体最小二乘(TLS)得到DOA估计。通过仿真实验将本文算法与TLS-ESPRIT算法、文献[16]中的CDNC-ESPRIT算法和NC-MSWF-FS算法进行比较，并对4种算法进行了复杂度分析，体现了本文算法的优越性。

1 数学模型

假设两个完全相同均匀线阵组成的平面传感器阵列，这两个子阵分别记为Zx和Zy，每个子阵都有M个阵元，阵元间距为d，子阵之间相差已知的位移矢量大小为δ，示意图如图 1所示。有K个远场窄带相干分布式非圆信号从θk(k=1,2,…,K)方向入射到该阵列上，波长为λ。

图1 双均匀线阵Fig.1 Double uniform linear array

两个子阵Zx和Zy的输出信号矢量分别为[5]

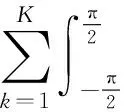
(1)

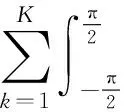
(2)

对于相干分布源，角信号密度函数可以表示为

sk(θ,t;μk)=sk(t)gk(θ;μk)

(3)

式中：sk(t)为第k个复随机信号源；gk(θ;μk)为相应的确定性角度加权函数，通常为高斯分布或均匀分布。进一步地，有

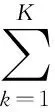
(4)

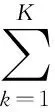
(5)

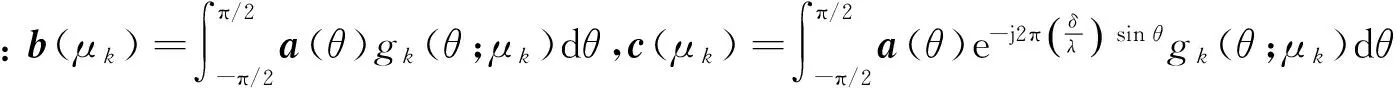
(6)

表示成矩阵形式为

C≈BΦ

(7)

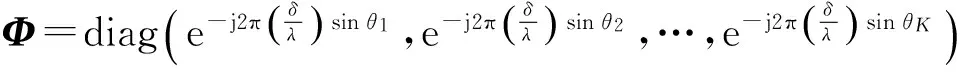
将子阵Zx和Zy的输出加以合并，构成整个阵列的输出信号矢量z(t)为

(8)

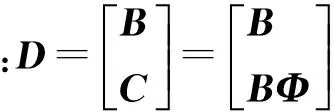
Z=DS+Nz

(9)

式中：

由上述分析知，阵列广义流型矩阵D具有旋转不变性，即

J1DΦ=J2D

(10)

式中：J1=[IM0M×M]和J2=[0M×MIM]分别为RM×2M的选择矩阵。

2 DOA快速估计算法

为有效提高估计精度和降低运算复杂度，算法在利用信号非圆特性扩展阵列输出矩阵的基础上，基于回溯优化的MSWF技术递推分解快速产生信号子空间，避免了通过复杂度较高的协方差矩阵特征分解获得信号子空间，最后由最小二乘或总体最小二乘求解出各个相干分布源DOA估计。图 2为整体算法流程。

图2 整体算法流程Fig.2 Integrated algorithm flow

2.1 阵列输出矩阵扩展

本文考虑接收信号为最大非圆率信号的情况，则接收信号矩阵S可以表示为[13]

S=ΨS0

(11)

式中：S0为实信号矩阵；Ψ=diag(ejφ1/2,ejφ2/2,…,ejφK/2)，其中φk为第k个相干分布源的非圆相位。

利用信号的非圆特性，可构造扩展的阵列输出矩阵Z(nc)∈C4M×N：

(12)

由式(10)知，广义阵列流型矩阵D具有旋转不变性，据此可以得到扩展后的广义阵列流型矩阵D(nc)也具有旋转不变性[21]：

(13)

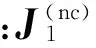
根据式(12)可知，利用扩展的阵列输出矩阵可以虚拟加倍阵元个数，进而可提高阵列的分辨精度，但运算量也随着阵列输出矩阵扩展后维数的增加而加大。

2.2 基于回溯优化的MSWF产生信号子空间

对得到的扩展阵列输出矩阵Z(nc)，传统的CDNC-ESPRIT算法通过计算协方差矩阵和特征分解虽然能得到准确可靠的信号子空间估计，但运算量相当大。而MSWF是一种有效的降维滤波技术，文献[18]证明了利用MSWF技术的前向多级递推分解特性可以快速获得观测数据的信号或噪声子空间，避免了计算协方差矩阵和特征分解，可大幅度降低运算量。

MSWF技术的基本思想是对观测信号进行多次正交投影分解，每次分解都得到两个相互正交的子空间，一个子空间平行于上一次观测信号与参考信号的互相关矢量，另一个则与之正交，然后对正交于互相关矢量的子空间再用相同的方法继续分解，以此类推，经过K(K<4M)次分解后可得到一个4M×K维矩阵，从而实现将观测信号投影到某一降维子空间。

将扩展阵列输出矩阵Z0=Z(nc)作为MSWF初始观测信号，利用满秩矩阵T1=[h1B1]对初始观测信号进行正交投影分解，可以得到两个子空间，一个子空间平行于h1，另一个子空间与h1正交，即为

(14)

初始参考信号d0的选取对信号子空间求解精度的影响很大，当信号波形未知时，可通过初始观测信号Z0来构造，一般有两种方式：Z0的第一行元素或者若干行元素的平均值，即

(15)

(16)

式中：e=[1 0 … 0]；m为行数。但由于实际应用中观测信号并不是无噪的，因此初始参考信号不可避免地引入噪声，进而使得MSWF递推分解过程中的各级匹配滤波器渗透了噪声子空间特征矢量，即是次优的，导致算法在低信噪比时性能较差。

本文针对此问题对MSWF的递推分解过程进行改进：在每级维纳滤波中，首先由前一级观测信号和参考信号的归一化互相关矢量得到次优匹配滤波器；然后引入回溯机制，利用该次优匹配滤波器通过投影的方法重新计算新的参考信号，实现参考信号的优化处理，从而再次通过前一级观测信号和新的参考信号的归一化互相关矢量得到优化后的匹配滤波器。考虑到多次回溯优化可进一步提升低信噪比时算法的估计性能，但不必要的重复优化会带来复杂度的增加，因此在回溯优化中，添加了一个优化终止判断过程，当优化后的参考信号与本次优化前的参考信号之间十分接近时，即两者的差值向量2-范数小于设定的阈值时，可停止回溯优化，否则继续优化。

本文基于回溯优化的MSWF技术产生信号子空间的具体步骤为

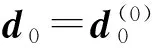
步骤2 通过前一级观测信号和参考信号的归一化互相关矢量得到次优匹配滤波器ht，有

(17)

(18)

(19)

步骤4 更新参考信号和观测信号，有

(20)

(21)

t=t+1，递推终止条件t>K，K为信源数。不满足终止条件，返回步骤2继续递推。

(22)

2.3 LS或TLS求解中心波达角

(23)

式中：Γ=TΦT-1，进而可以通过最小二乘准则或者总体最小二乘准则求解出Γ。

Γ的特征值是Φ的对角元素，得到矩阵Γ就可以利用其特征值估计出DOA：

(24)

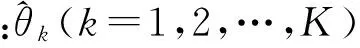
2.4 算法步骤

根据上述分析可以将本文估计相干分布式非圆信号DOA的方法归纳为以下步骤。

步骤1 对阵列输出信号根据式(12)进行扩展，得到扩展阵列输出矩阵Z(nc)。

步骤2 获取MWSF初始观测信号Z0=Z(nc)和初始参考信号d0。

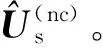
步骤4 由2.3节中最小二乘或总体最小二乘准则求解出K个相干分布源DOA估计值。

3 仿真实验

3.1 仿真分析

本文研究的是非圆信号下的相干分布式信源DOA估计算法，拟采用角信号密度函数为高斯分布的相干分布式BPSK信号作为发射信号。仿真实验采用如图 1所示的阵列结构，阵元间距d=λ/2，两个子阵间距δ=λ/10。实验中假设噪声为高斯白噪声。为了验证本文算法的实用性和鲁棒性，采用蒙特卡罗实验将本文算法与TLS-ESPRIT、CDNC-ESPRIT和NC-MSWF-FS算法进行对比分析。

定义均方根误差(Root Mean Square Error， RMSE)为

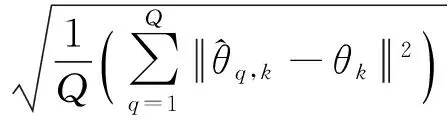
k=1,2,…,K

(25)

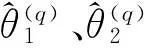
定义DOA估计误差为

(26)

根据式(26)计算出Δθq,1、Δθq,2，图4为DOA估计误差的分布图。定义DOA估计误差的均值为

(27)

其他参数不变的条件下，令SNR=0 dB，得

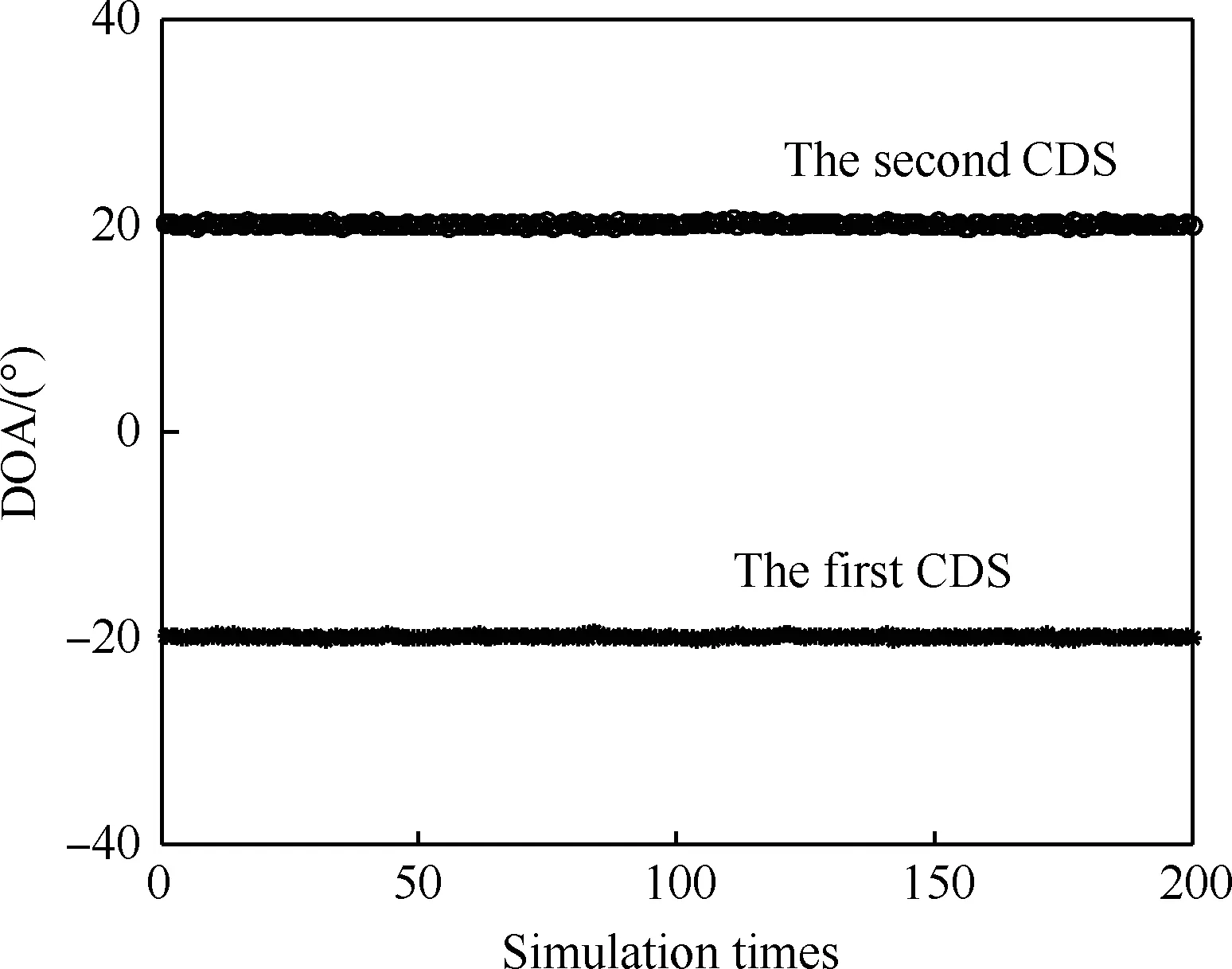
图3 DOA估计值分布(SNR=15 dB， K=2) Fig.3 Distribution of DOA estimation (SNR=15 dB,K=2)

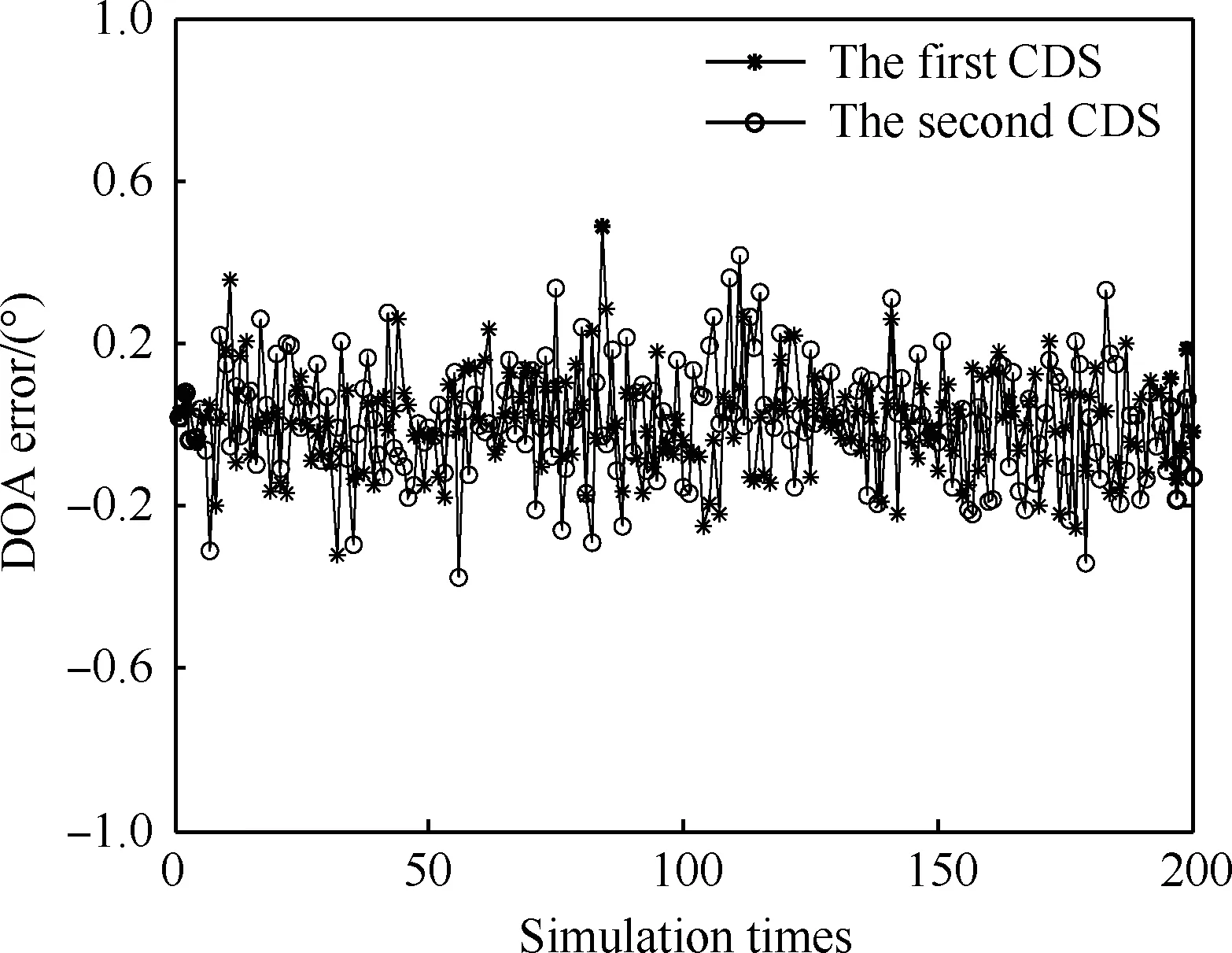
图4 DOA估计误差值分布(SNR=15 dB， K=2) Fig.4 Distribution of DOA estimation error (SNR=15 dB, K=2)

到DOA估计值分布图如图5所示。由图5可以看出虽然随着信噪比的下降，DOA估计值分布趋于发散，但其均值仍接近真实值。因此本文算法在低信噪比下依旧有着较强的鲁棒性。

仿真2 算法性能对比：将本文算法与TLS-ESPRIT、CDNC-ESPRIT和NC-MSWF-FS算法性能进行对比。假设信源数K=3，波达方向分别为(-20°,5°,15°)，对应角度扩展分别为(3°,4°,5°)，分别绘制这些算法的RMSE曲线与信噪比的关系，曲线如图6所示。从图中可以看出本文算法与CDNC-ESPRIT算法的估计性能近似相同，但明显优于TLS-ESPRIT算法。这是因为本文算法与 CDNC-ESPRIT算法均利用信号非圆特性扩展了阵列接收矩阵，虚拟增大了阵元数，扩展了阵元孔径，从而提高了估计性能。NC-MSWF-FS算法虽然也利用了信号非圆特性，但由于初始参考信号中噪声的影响导致MSWF递推分解得到的信号子空间在低信噪比时精度较差，而本文算法在MSWF递推分解过程中引入了回溯优化机制，所以本文算法在低信噪比时性能明显优于NC-MSWF-FS算法。

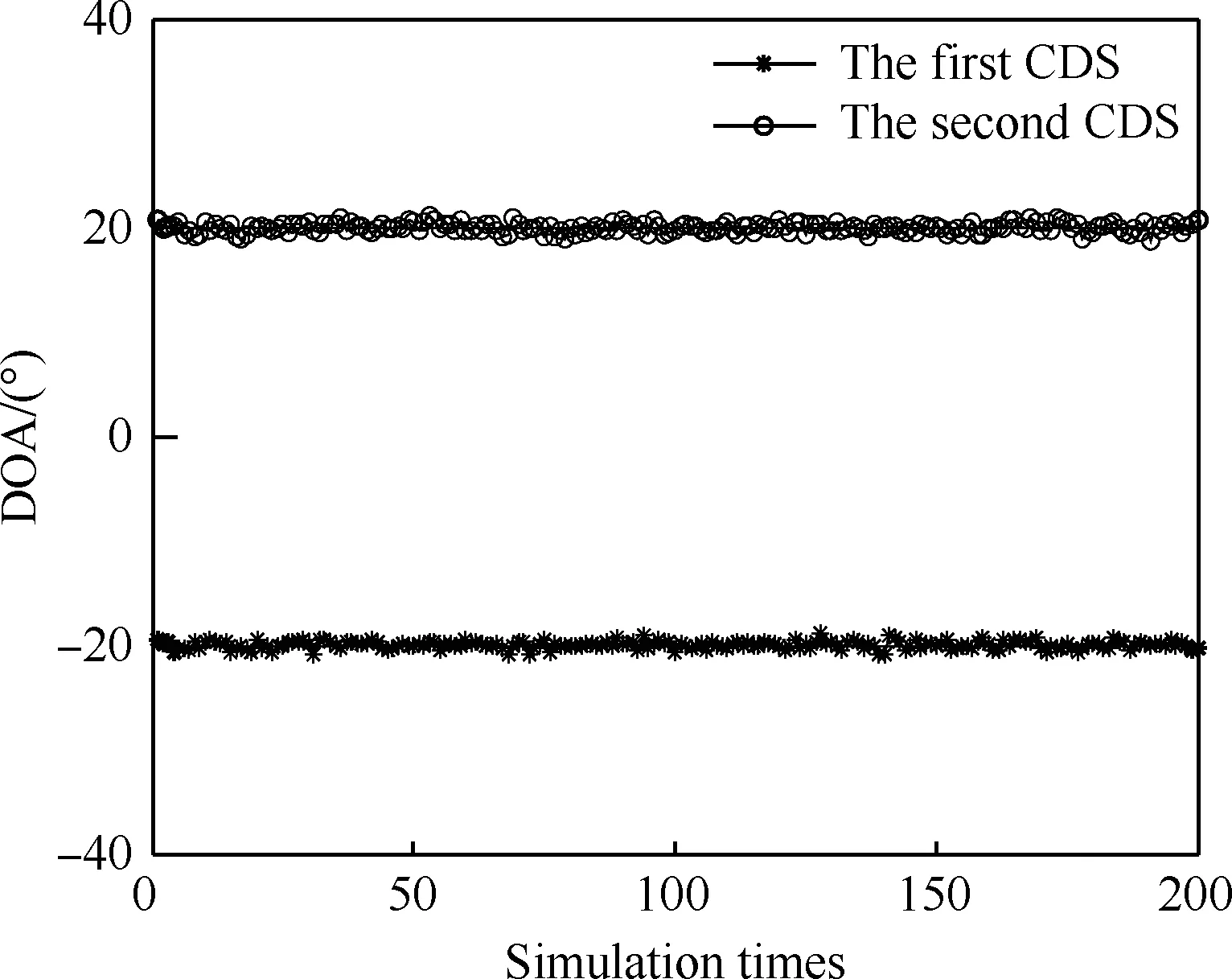
图5 DOA估计值分布(SNR=0 dB， K=2) Fig.5 Distribution of DOA estimation (SNR=0 dB,K=2)

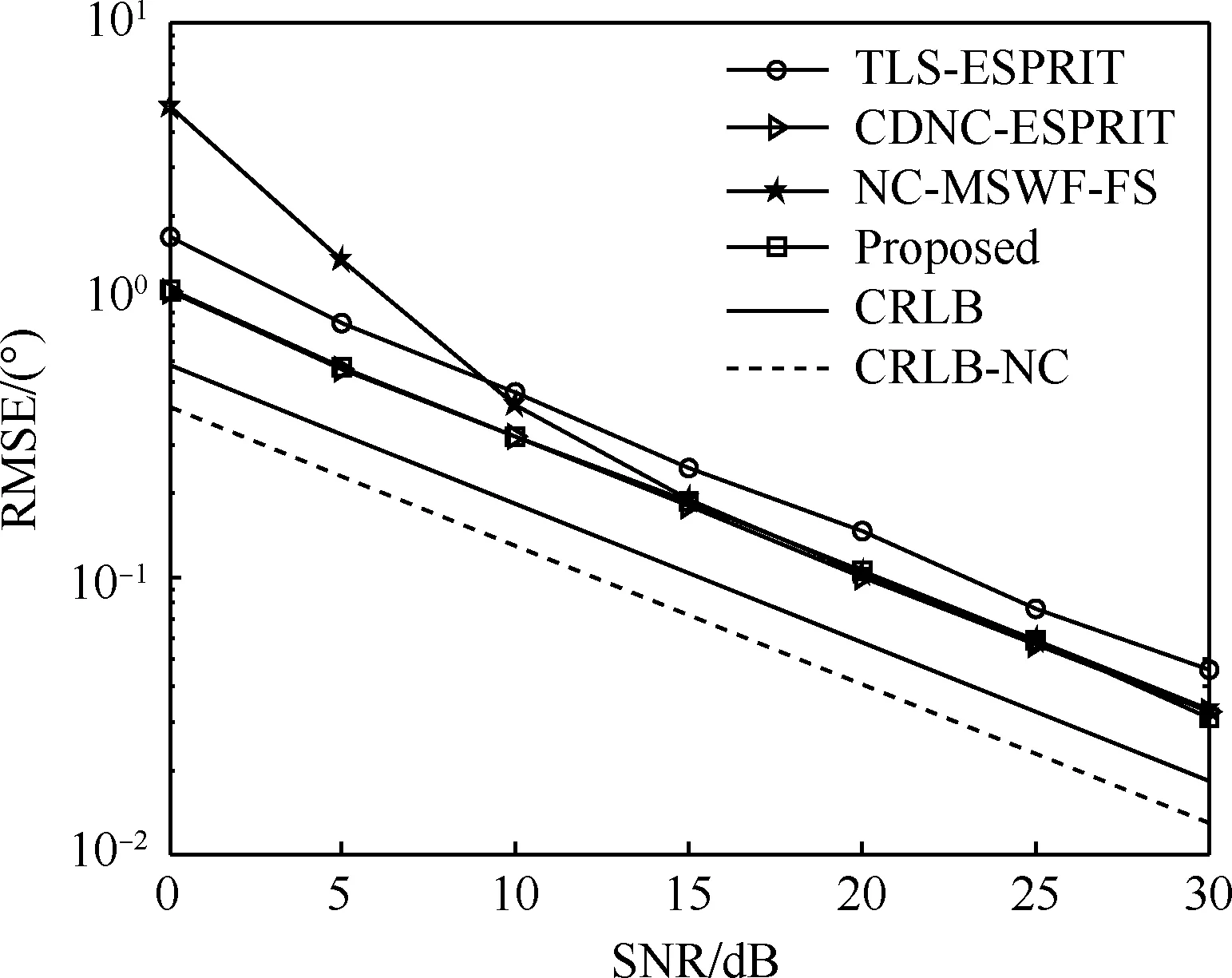
图6 不同算法均方根误差与信噪比的关系Fig.6 Relationship between RMSE and SNR of different algorithm

仿真3 初始参考信号的影响：在相同仿真条件下，为比较MSWF不同初始参考信号对本文算法和NC-MSWF-FS算法各自估计性能的影响，选取初始参考信号为初始观测信号矩阵Z0第1行元素、前M行元素平均值、前2M行元素平均值、前3M行元素平均值和前4M行元素平均值这5种情况，绘制各自的RMSE曲线与信噪比SNR的关系，如图7所示，固定信噪比为0 dB，绘制各自的RMSE曲线与快拍数的关系，如图 8所示。由图7、图 8可以看出NC-MSWF-FS算法的估计性能受初始参考信号的影响波动较大，鲁棒性较差，并且这5种选取方式下的估计性能在低信噪比时均低于CDNC-ESPRIT算法，而本文算法的估计性能受初始参考信号的影响波动很小，并且5种选取方式下的估计性能都与CDNC-ESPRIT算法非常接近，因此本文算法对初始参考信号的选取具有很强的鲁棒性，初始参考信号的任意选取不会导致本文算法在低信噪比时性能的下降。

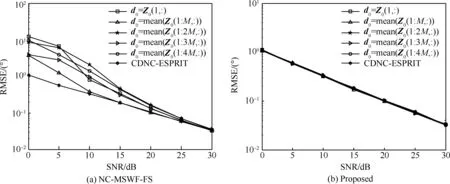
图7 不同初始参考信号下均方根误差与信噪比的关系Fig.7 Relationship between RMSE and SNR of different initial reference signals

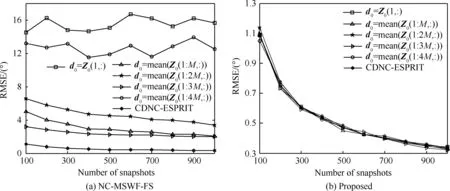
图8 不同初始参考信号下均方根误差与快拍数的关系Fig.8 Relationship between RMSE and number of snapshots of different initial reference signals

3.2 复杂度分析

TLS-ESPRIT算法的计算复杂度主要包括两部分：估计一个2M阶的阵列协方差矩阵和对该阵列协方差矩阵进行特征分解，复杂度为O(4M2N+8M3)；总体最小二乘准则计算DOA估计，复杂度为O(4K2M+11K3)。文献[16]提出的CDNC-ESPRIT算法的计算复杂度主要包括两部分：估计一个4M阶的阵列协方差矩阵和对该阵列协方差矩阵进行特征分解，复杂度为O(16M2N+64M3)；总体最小二乘准则计算DOA估计，复杂度为O(8K2M+11K3)。NC-MSWF-FS算法采用MSWF技术获取信号子空间，无须计算阵列协方差矩阵及特征分解，计算复杂度包括：用MSWF技术估计信号子空间，复杂度为O(12KMN)；总体最小二乘准则计算DOA估计，复杂度为O(4K2M+11K3)。本文算法在MSWF递推分解过程中引入了回溯优化机制，复杂度为O(12(h+1)KMN+4K2M+11K3)(h≥1为回溯优化次数)。表1为4种算法复杂度对比表。图9 为4种算法的归一化运行时间对比。

表1 不同算法复杂度对比表Table 1 Comparison of different algorithm complexity

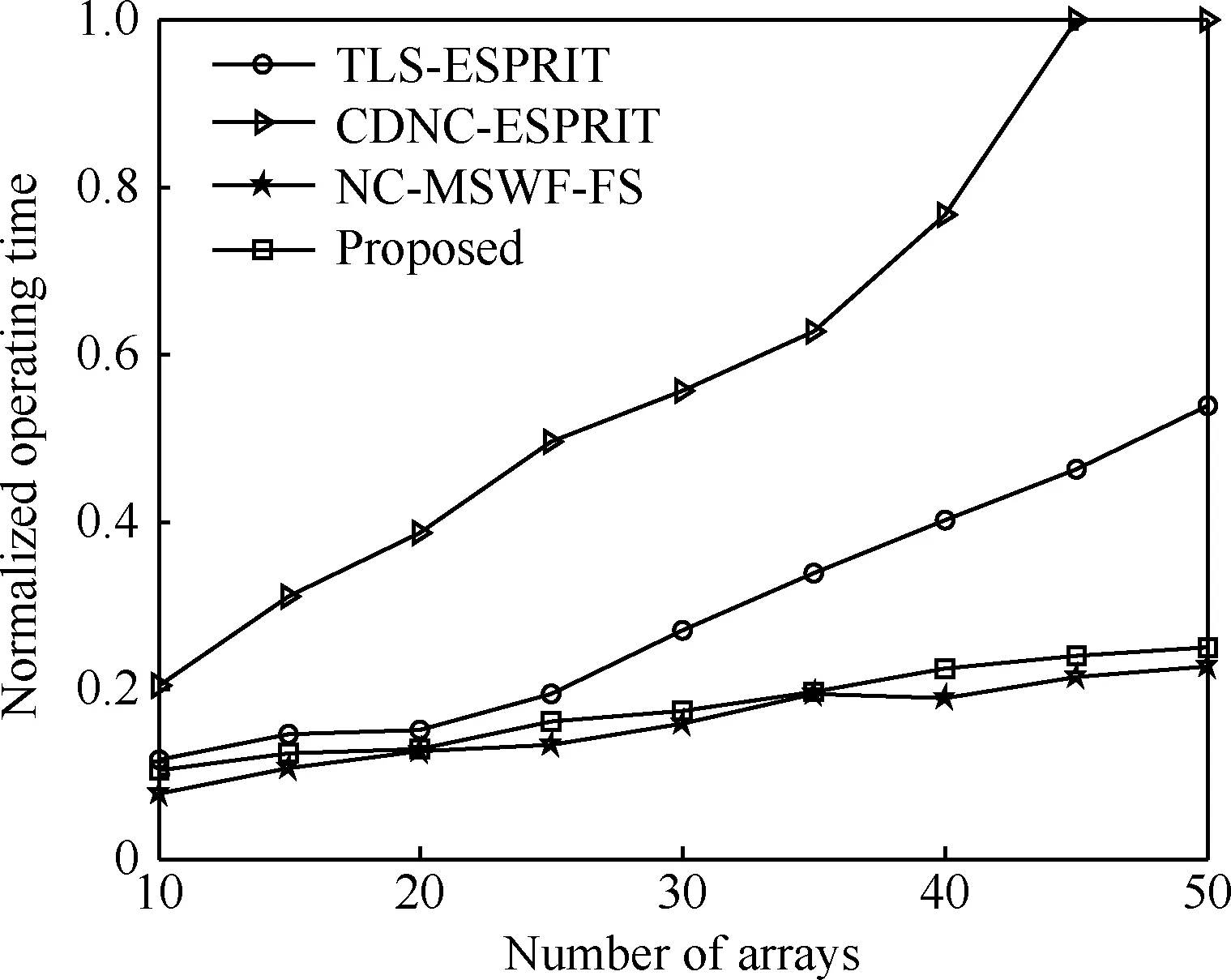
图9 归一化运行时间与阵元数的关系Fig.9 Relationship between normalized operating time and number of arrays

由表 1、图 9可以看出，TLS-ESPRIT算法和CDNC-ESPRIT算法复杂度随阵元数M增加呈指数级增加。而本文算法的复杂度在阵元数较大时远低于CDNC-ESPRIT算法，并且相较于NC-MWSF-FS算法复杂度增加较小。根据以上分析，可以得出这样的结论：本文算法相比于CDNC-ESPRIT算法，在保持估计精度的同时大幅度降低了复杂度，而相比于NC-MWSF-FS算法，在较小复杂度的代价下取得了性能的较大提升。

4 结 论

在相干分布式非圆信号DOA估计中，针对利用信号非圆特性带来的较大运算量和降维的MSWF技术受初始参考信号选取影响较大的问题，本文提出来一种基于回溯优化降维的DOA快速估计算法。该算法具有如下优势：

1) 与 CDNC-ESPRIT算法相比，本文算法直接通过递推分解快速求出信号子空间，避免了计算协方差矩阵及其特征分解运算，在保持估计精度的同时大幅度降低了运算复杂度。

2) 相比于传统的MSWF算法，本文算法在递推分解过程中引入了回溯优化机制提高了各级匹配滤波器的估计性能，在较小复杂度的代价下取得了性能的较大提升，并且对初始参考信号的选取具有很强的鲁棒性。

[1] 潘捷, 周建江, 汪飞. 非均匀噪声稀疏均匀圆阵的二维DOA估计[J]. 航空学报, 2011, 32(3): 448-456.

PAN J, ZHOU J J, WANG F. 2-D DOA estimation for sparse uniform circular array in presence of unknown nonuniform noise[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(3): 448-456 (in Chinese).

[2] YANG B, HE F, JIN J, et al. DOA estimation for attitude determination on communication satellites[J]. Chinese Journal of Aeronautics, 2014, 27(3): 670-677.

[3] 曾文浩, 朱晓华, 李洪涛, 等. 一种稀疏阵列下的二维DOA估计方法[J]. 航空学报, 2016, 37(7): 2269-2275.

ZENG W H, ZHU X H, LI H T, et al. A 2D DOA estimation method for sparse array[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2269-2275 (in Chinese).

[4] 郑植. 分布式信源低复杂度参数估计算法研究[D]. 成都： 电子科技大学, 2011.

ZHENG Z. Research on low complexity parameter estimation algorithm for distributed source[D]. Chengdu: University of Electronic Science and Technology, 2011 (in Chinese).

[5] SHAHBAZPANAHI S, VALAEE S, BASTANI M H. Incoherently distributed source localization[J]. Scientia Iranica, 2000, 7(3): 244-252.

[6] LEE S R, SONG I, LEE Y U, et al. Estimation of two-dimensional DOA under a distributed source model and some simulation results[J]. IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, 1996, 79(9): 1475-1485.

[7] VALAEE S, CHAMPAGNE B, KABAL P. Parametric localization of distributed sources[J]. IEEE Transactions on Signal Processing, 1995, 43(9): 2144-2153.

[8] SHAHBAZPANAHI S, VALAEE S, BASTANI M H. Distributed source localization using ESPRIT algorithm[J]. IEEE Transactions on Signal Processing, 2001, 49(10): 2169-2178.

[9] LEE J, JOUNG J, KIM J D. A method for the direction-of-arrival estimation of incoherently distributed sources[J]. IEEE Transactions on Vehicular Technology, 2008, 57(5): 2885-2893.

[10] SIESKUL B T. An asymptotic maximum likelihood for joint estimation of nominal angles and angular spreads of multiple spatially distributed sources[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3): 1534-1538.

[11] GAN L, WANG X Q, LIAO H S. DOA estimation of coherently distributed sources based on block-sparse constraint[J]. IEICE Transactions Communication, 2012, 95(7): 2472-2476.

[12] 刘章孟, 周一宇, 吴海斌, 等. 非圆信号的贝叶斯稀疏重构阵列测向方法[J]. 航空学报, 2014, 35(3): 821-827.

LIU Z M, ZHOU Y Y, WU H B. Direction of arrival estimation method of non-circular signals via sparse Bayesian reconstruction[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 821-827 (in Chinese).

[13] 尹洁昕, 吴瑛, 王鼎. 基于辅助阵元的非圆信号自校正算法及其性能分析[J]. 通信学报, 2014(2): 153-165.

YIN J X, WU Y, WANG D. Auto-calibration method and performance analysis for noncircular sources based on instrumental sensors[J]. Journal on Communications, 2014(2): 153-165 (in Chinese).

[14] 杨学敏, 李广军, 郑植. 基于稀疏表示的相干分布式非圆信号的参数估计[J]. 电子与信息学报, 2014, 36(1): 164-168.

YANG X M, LI G J, ZHENG Z. Parameters estimation of coherently distributed non-circular signal based on sparse representation[J]. Journal of Electronics and Information Technology, 2014, 36(1): 164-168 (in Chinese).

[15] WAN L, HAN G, JIANG J, et al. DOA estimation for coherently distributed sources considering circular and noncircular signals in massive MIMO systems[J]. IEEE Systems Journal, 2017， 11(1)： 41-49.

[16] YANG X, LI G, ZHENG Z, et al. 2D DOA estimation of coherently distributed noncircular sources[J]. Wireless Personal Communications, 2014, 78(2): 1095-1102.

[17] SONG N, DE LAMARE R C, HAARDT M, et al. Adaptive widely linear reduced-rank interference suppression based on the multistage wiener filter[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4003-4016.

[18] 黄磊, 吴顺君, 张林让, 等. 快速子空间分解方法及其维数的快速估计[J]. 电子学报, 2005, 33(6): 977-981.

HUANG L, WU S J, ZHANG L R, et al. Fast method for subspace decomposition and its dimension estimation[J]. Acta Electronica Sinica, 2005, 33(6): 977-981 (in Chinese).

[19] 宋爱民, 李堰, 刘剑, 等. 非圆信号多级维纳滤波DOA估计求根算法[J]. 电子科技大学学报, 2013, 42(1): 53-57.

SONG A M, LI Y, LIU J, et al. DOA estimation of noncircular signals with multistage wiener filter and polynomial rooting[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(1): 53-57 (in Chinese).

[20] ZENG Y, YANG Y, LU G, et al. Fast method for DOA estimation with circular and noncircular signals mixed together[J]. Journal of Electrical & Computer Engineering, 2014, 2014: 1-7.

[21] STEINWANDT J, ROEMER F, HAARDT M, et al.R-dimensional ESPRIT-type algorithms for strictly second-order non-circular sources and their performance analysis[J]. IEEE Transactions on Signal Processing, 2015, 62(18): 4824-4838.

(责任编辑： 苏磊)

*Corresponding author. E-mail: xinxidailiang@outlook.com

Fast DOA estimation for coherently distributed noncircular sources by backtracking reduced dimension

DAI Zhengliang*, BA Bin, ZHANG Yankui, CUI Weijia, WANG Daming

InstituteofInformationSystemEngineering,PLAInformationEngineeringUniversity,Zhengzhou450001,China

In the estimation of Direction of Arrival (DOA) for coherently distributed noncircular (CDNC) signals, the increase of dimension caused by array output matrix extension can bring a large amount of computation. For the problem, a fast estimation algorithm based on the Multi-Stage Wiener Filter (MSWF) technology is proposed by introducing the idea of backtracking optimization. The proposed algorithm first uses the noncircularity of the signal to extend the array output matrix. The signal subspace is then obtained by using the recursive decomposition characteristic of the MSWF, so as to avoid the computation of the covariance matrix and the characteristic decomposition of the matrix. In the recursive decomposition process, the backtracking optimization mechanism is introduced to improve the estimation performance of the matched filter. The DOA estimation can be obtained by the Least Squares (LS) or the Total Least Squares (TLS). Simulation results show that the performance of the proposed algorithm with a much lower complexity is comparable with the rotation invariant subspace algorithm based on CDNC (CDNC-ESPRIT). Compared to the fast noncircular signal subspaced algorithm based on the MSWF (NC-MSWF-FS), the proposed algorithm can effectively improve performance at lower complexity cost in low signal to noise ratio. The simulation also shows that the proposed algorithm is more robust to the initial reference signal.

coherently distributed source； noncircular source； multi-stage Wiener filter (MSWF)； backtracking optimization； recursive decomposition

2016-12-07； Revised： 2017-02-06； Accepted： 2017-03-15； Published online： 2017-03-23 17:50

URL： www.cnki.net/kcms/detail/11.1929.V.20170323.1750.010.html

National Natural Science Foundation of China (61401513)

V19； TN911.72

A

1000-6893(2017)09-321034-10

2016-12-07； 退修日期： 2017-02-06； 录用日期： 2017-03-15； 网络出版时间： 2017-03-23 17:50

www.cnki.net/kcms/detail/11.1929.V.20170323.1750.010.html

国家自然科学基金(61401513)

*通讯作者.E-mail: xinxidailiang@outlook.com

代正亮， 巴斌， 张彦奎， 等． 回溯降维相干分布式非圆信号DOA快速估计[J]． 航空学报, 2017, 38(9): 321034. DAI Z L, BA B, ZHANG Y K, et al. Fast DOA estimation for coherently distributed noncircular sources by backtracking reduced dimension[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 321034.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321034